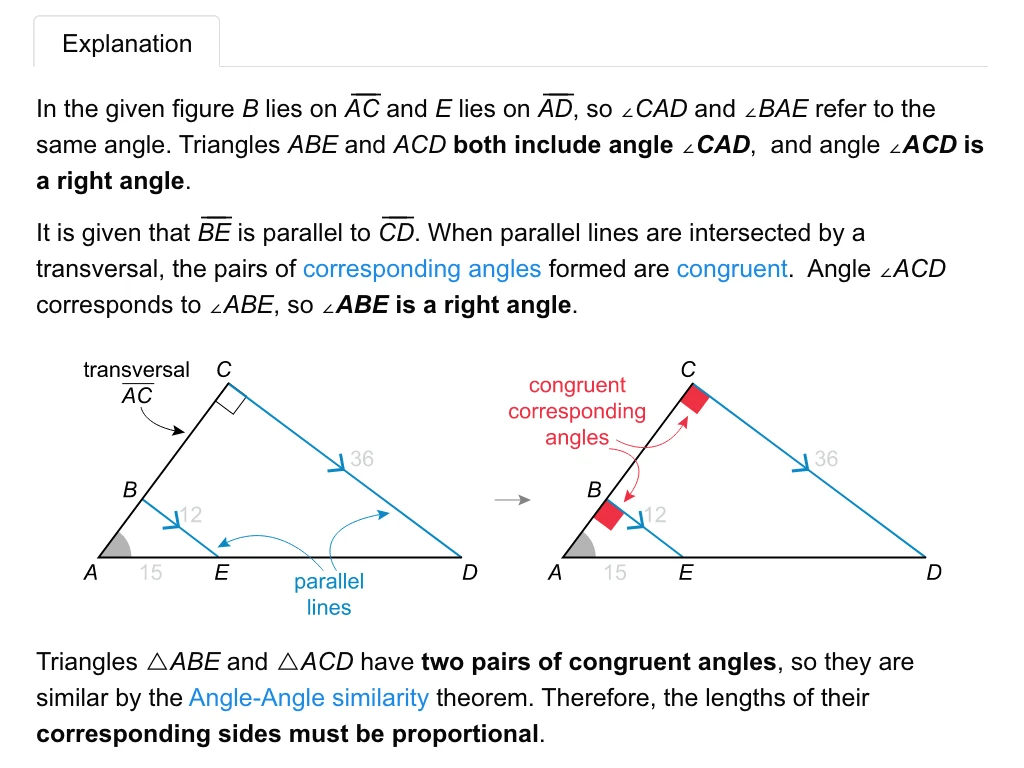
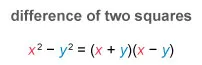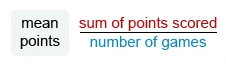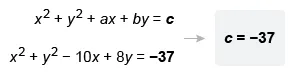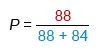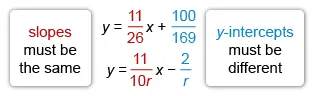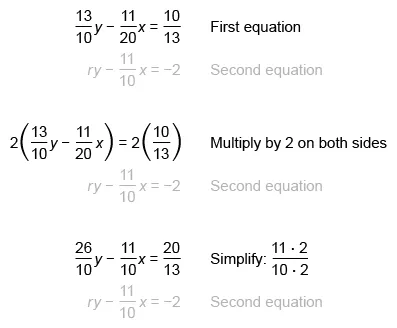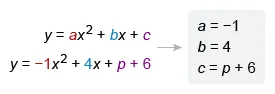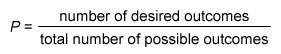SAT Math Sample Questions and Problems with Answers
See what the SAT Math section is really like with interactive sample questions and detailed explanations. Explore real exam-style problems that test your ability to apply math concepts, reason through data, and solve practical problems efficiently.
SAT Math Sample Test Questions by Topic
SAT Math Algebra Sample Problems
Question
If a − b = 3 and a + b = 4, what is the value of (a − b)(a2 − b2) ?
Factor the expression (a2 − b2) as a difference of two squares.
Explanation
Notice that the given expression contains a difference of two squares () and a factor with a given value ().
A difference of two squares of the form can be factored as .
The difference of two squares in the given expression can be factored as , and both factors have given values. To evaluate , first factor as a difference of two squares.
| (a − b)(a2 − b2) | Given expression |
| (a − b)(a + b)(a − b) | Factor a2 − b2 |
Now plug in the given values for each of the factors = 3 and = 4.
| (a − b)(a + b)(a − b) | |
| (3)(4)(3) | Substitute (a − b) = 3 and (a + b) = 4 |
| 36 | Multiply |
The value of is .
Things to remember:
- An expression of the form is a difference of two squares that can be factored as .
- If the value for an expression is given, it may be possible to rewrite a desired expression in terms of the given expression and plug in known values.
Question
What is the solution set of the equation above?
| A. {−4} | |
| B. {0} | |
| C. {3} | |
| D. {3, 4} |
Hint :
To solve a rational equation, first multiply both sides by the least common denominator (LCD) to clear the fractions.
Explanation
The given equation is a rational equation because it contains a variable in a denominator. Solutions to a rational equation may be valid or extraneous, so solve for x and then check for extraneous solutions.
The only denominator in is x − 3, so multiply both sides of the equation by x − 3 to clear the fraction.
| Given equation | |
| Multiply both sides by (x − 3) | |
| Cancel factors to clear fraction | |
| Simplify |
To solve the resulting quadratic equation, rewrite it in standard form ax² + bx + c = 0 and then factor.
| Distribute −1 to (x − 3) | |
| Add x and subtract 3 on both sides | |
| Factor |
The expression (x + 4)(x − 3) is equal to 0 when either of its factors equals 0. Set each factor equal to 0 to solve for x.
| x + 4 = 0 | Set each factor equal to 0 | x − 3 = 0 |
| x = −4 | Solve for x | x = 3 |
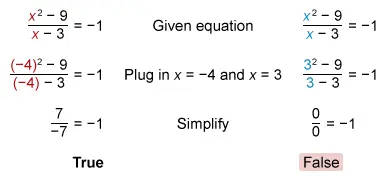
Plug x = −4 and x = 3 into the given equation and simplify to check if they are valid or extraneous.
The solution x = −4 results in a true statement, so
−4 is a valid solution.
The solution x = 3 results in a false statement, so
3 is an extraneous solution.
Therefore, the solution set of the given equation is {−4}.
Elimination strategy: It is possible to identify values of x where the given equation is undefined to eliminate Choices C and D.
(Choice B) 0 is not in the solution set, because 0 does not satisfy the given equation (see alternate method).
(Choice C) 3 is an extraneous solution, because the left side of the given equation simplifies to the undefined fraction when x = 3. Therefore, 3 is not in the solution set.
(Choice D) 3 and 4 may result from a combination of a sign error and the error described in Choice C.
Things to remember:
- An equation that contains a variable in a denominator is a rational equation. To solve a rational equation, multiply both sides by the least common denominator (LCD) to clear the fractions.
- Solutions to a radical equation may be valid or extraneous, so solve the equation and then plug the results into the given equation to check for extraneous solutions.
- A rational equation is undefined when any variable denominator is equal to zero.
Alternate Method :
It is also possible to plug each possible solution from the choices into the given equation to determine the solution set. The choices include −4, 0, 3, and 4 as possible solutions.
Plug x = −4, x = 0, x = 3, and x = 4 into to see which simplifies to a true statement.
Of the values from the choices, only −4 simplifies the equation to a true statement. Therefore, the solution set of the given equation is {−4}.
Note: When x = 3, the left side of the given equation simplifies to the undefined fraction .
Things to remember:
Any value that simplifies an equation to a true statement is a solution to the equation.
Question
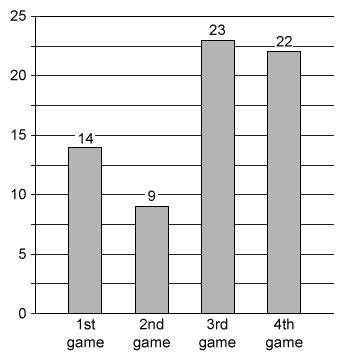
The bar graph shows the number of points scored by a football team in each of four games. For these four games, how much greater is the median number of points scored than the mean number of points scored?
Hint :
The mean of a data set is the sum of the values divided by the number of values.
The median is the middle of a data set when all values are ordered numerically.
Explanation
To find how much greater the median number of points is than the mean number of points, calculate each measure separately and then subtract the mean from the median.
First identify from the given bar graph that the numbers of points scored in the 4 games were 14, 9, 23, and 22.
Mean score
The mean of a data set is the sum of the values divided by the number of values.
The sum of the values is the sum of the numbers of points scored and the number of values is the number of games.
Plug the numbers of points (14, 9, 23, and 22) and the number of games (4) into the expression for the mean and simplify to calculate the mean score.
| Mean number of points | |
| Plug in values | |
| Add in numerator | |
| Divide |
The mean number of points is 17.
Median score
The median is the middle of a data set when all values are ordered numerically. For a data set with an even number of values, the median is the average of the middle two.
The numbers of points scored are 14, 9, 23, and 22. Order these values numerically and then calculate the average of the middle two to find the median number of points scored.
The median number of points is 18.
The mean is 17 points and the median is 18 points. Subtract 18 − 17 = 1 to see that the median is 1 point greater than the mean.
Things to remember:
- The mean of a data set is the sum of the values divided by the number of values.
- The median is the middle of a data set when all values are ordered numerically. For a data set with an even number of values, the median is the average of the middle two.
SAT Math Advanced Math Sample Questions
Question
An equation of a circle in the xy-plane with radius 2 and center at (5, −4) is x2 + y2 + ax + by = c. What is the value of c ?
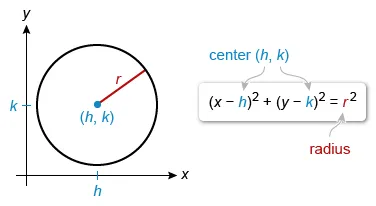
The equation of a circle in standard form is (x − h)2 + (y − k)2 = r 2, where (h, k) is the center and r is the length of the radius.
Explanation
The equation of a circle in standard form is (x − h)2 + (y − k)2 = r 2, where (h, k) is the center and r is the length of the radius.
The given circle has radius 2 and center at (5, −4), so plug in r = 2 and (h, k) = (5, −4) to get an equation of the circle in standard form. Then rewrite the equation in the form x2 + y2 + ax + by = c to identify the value of c.
| (x − h)2 + (y − k)2 = r 2 | Standard form |
| (x − 5)2 + (y − (−4))2 = 22 | Plug in (h, k) = (5, −4) and r = 2 |
| (x − 5)2 + (y + 4)2 = 4 | Simplify |
Now expand the perfect squares (x − 5)2 and (y + 4)2 and then rearrange the equation to the form x2 + y2 + ax + by = c.
| (x − 5)2 + (y + 4)2 = 4 | |
| x2 − 10x + 25 + y2 + 8y + 16 = 4 | Expand (x − 5)2 and (y + 4)2 |
| x2 + y2 − 10x + 8y + 41 = 4 | Rearrange and combine constant terms on left |
| x2 + y2 − 10x + 8y = −37 | Subtract 41 from both sides |
Compare the resulting equation to the given equation to identify c.
Things to remember:
-
The equation of a circle in standard form is (x − h)2 + (y − k)2 = r 2, where (h, k) is the center and r is the length of the radius.
-
To expand (a + b)2, use the identity (a + b)2 = a2 + 2ab + b2 or rewrite the expression (a + b)2 as (a + b)(a + b) and multiply.
Question
In a warehouse, there are 7 shelves of cardboard boxes and 8 shelves of plastic boxes. Each shelf of cardboard boxes has 12 boxes that weigh 25 pounds or more and 8 boxes that weigh less than 25 pounds. Each shelf of plastic boxes has 11 boxes that weigh 25 pounds or more and 9 boxes that weigh less than 25 pounds. A box from one of these shelves will be selected at random. What is the probability of selecting a plastic box, given that the box is 25 pounds or heavier?
To find the probability of a desired event, use the following formula:
Explanation
The question asks for the probability of selecting a plastic box, given that the box is 25 pounds or heavier.
To find the probability of a desired event, use the following formula:
The total number of possible outcomes is the total number of boxes that are 25 pounds or heavier.
The number of desired outcomes is the number of those boxes that are plastic.
The total boxes that weigh 25 pounds or more is the sum of the numbers of plastic boxes and cardboard boxes that weigh 25 pounds or more.
It is given that there are 8 shelves with 11 plastic boxes on each shelf that weigh 25 pounds or more and that there are 7 shelves with 12 cardboard boxes on each shelf that weigh 25 pounds or more.
Multiply each number of shelves by the number of boxes on each shelf to see that there are 8 ∙ 11 = 88 plastic boxes and there are 7 ∙ 12 = 84 cardboard boxes that weigh 25 pounds or more.
Now simplify the probability.
| Add in denominator | |
| Simplify: |
The probability of selecting a plastic box, given that the box is 25 pounds or heavier, is
Things to remember:
To find the probability of a desired event, use the following formula:
Question
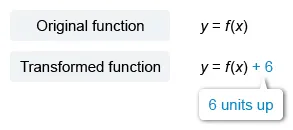
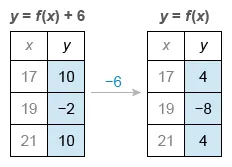
The table shows three values of x and their corresponding values of y, where y = f(x) + 6 and f is a quadratic function. What is the y-coordinate of the y-intercept of the graph of y = f(x) in the xy-plane?
For any function f(x), the graph of y = f(x − h) + k is the graph of y = f(x) transformed by a horizontal shift of h units and a vertical shift of k units.
The equation of a quadratic function in vertex form is y = a(x − h)2 + k, where (h, k) is the vertex of the parabola and a is the scale factor.
Explanation
The equation is in terms of , so it is the result of a transformation to the function . The constant 6 is added to the output , so it represents a vertical shift 6 units up.
Each row of the table represents an (x, y) point on the graph of . The question asks for the y-intercept of , so apply the transformation to the given table to get a table of values for .
Every point on the graph of is 6 units above a point on the graph of , so subtract 6 from each y-value to get a table that represents points on the graph of .
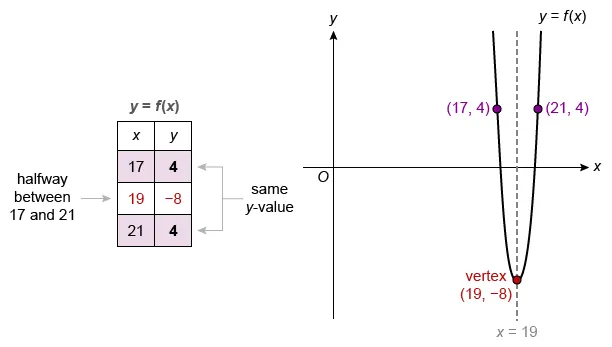
It is given that f(x) is a quadratic function, so its graph is a parabola. A vertical axis of symmetry passes through the vertex and is located halfway between any two points on a parabola that have the same y-value.
Notice that two points from the table have the same y-value (4). Therefore, the point with an x-value halfway between 17 and 21 is the vertex (h, k). This point is in the table (19, −8).
Plug (h, k) = (19, −8) into the vertex form equation to see that an equation for the graph of f(x) is . Plug in a different point from the table to solve for a. Choose (x, y) = (17, 4).
| y = a(x − 19)² − 8 | |
| 4 = a(17 − 19)² − 8 | Plug in x = 17 and y = 4 |
| 4 = a(−2)² − 8 | Subtract inside parentheses |
| 4 = 4a − 8 | Apply the exponent |
| 12 = 4a | Add 8 to both sides |
| 3 = a | Divide by 4 on both sides |
Plug a = 3 into to see that an equation for f(x) is . To find the y-coordinate of the y-intercept, plug in x = 0 and solve for y.
| y = 3(x − 19)² − 8 | |
| y = 3(0 − 19)² − 8 | Plug in x = 0 |
| y = 3(−19)² − 8 | Subtract inside parentheses |
| y = 3(361) − 8 | Apply the exponent |
| y = 1,075 | Simplify |
Note: It is also possible to use the given table of values to see that the equation of the transformed function is and has y-intercept 1,081. Then subtract 6 to get the y-coordinate of the y-intercept of .
Things to remember:
- For any function , the graph of is the graph of transformed by a horizontal shift of h units and a vertical shift of k units.
- A vertical axis of symmetry passes through the vertex (h, k) of a parabola and is located halfway between any two points on a parabola that have the same y-value.
- The equation of a quadratic function in vertex form is , where (h, k) is the vertex of the parabola and a is the scale factor.
SAT Math Problem-Solving and Data Analysis Sample Questions
Question
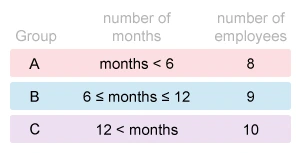
A small company classifies its employees according to how long they have been employed. Eight employees have worked at the company for less than 6 months and are classified in Group A. Nine employees have worked at the company for at least 6 months but no more than 12 months and are classified in Group B. Ten employees have worked at the company for more than 12 months and are classified in Group C. Which of the following could be the median amount of time, in months, that these 27 employees have worked at the company?
| A. 5.5 | |
| B. 7 | |
| C. 12.5 | |
| D. 16 |
Hint :
The median of a data set is the middle of the set when all values are ordered numerically.
Explanation
The median of a data set is the middle of the set when all values are ordered numerically. When the number of values is odd, the median is the middle value.
The number of months each employee has worked at the company is unknown, but the range of months for each group is given. First consider the groups from least to greatest according to the ranges of months worked.
It is given that there are 27 employees, so the median number of months must be the number worked by the 14th employee (proof).
Starting with the first range, add the number of employees in each successive group to find the group that contains the 14th employee and identify the range of months that employee has worked.
The 14th employee was in Group B, so the 14th employee worked at least 6 months and no more than 12 months.
Of the choices, only Choice B falls within this range. Therefore, the median number of months could be 7.
(Choices A, C, and D) These choices are not possible numbers of months because they do not fall within the range worked by the 14th employee (at least 6 months and no more than 12 months).
Things to remember:
The median of a data set is the middle of the set when it is ordered numerically. When the total number of values is odd, the median is the middle value. When it is even, the median is the average of the middle two values.
Question
In a tall office building, an express elevator descends from a height of 300 feet to 20 feet at a constant rate of 8 feet per second. What type of function best models the relationship between the height of the descending elevator and time?
| A. Increasing linear | |
| B. Decreasing linear | |
| C. Increasing exponential | |
| D. Decreasing exponential |
Hint :
A function is linear if the same number is added to each value to get the next. A function is exponential if the same number is multiplied by each value to get the next.
Explanation
A function is linear if the same number is added to each value to get the next (the difference is constant).
A function is exponential if the same number is multiplied by each value to get the next (the ratio is constant).
It is given that the elevator descends 8 feet per second, so the same number (−8) is added every second. Therefore, the function is linear.
As the number of seconds increases, the height of the elevator decreases. Therefore, the function is decreasing.
The function that best models the relationship between the height of the elevator and time is decreasing linear.
(Choice A) "Increasing linear" is incorrect because as time increases, the height of the elevator decreases.
(Choice C) "Increasing exponential" may result from the combination of errors described in Choices A and D.
(Choice D) "Decreasing exponential" is incorrect because the same number is added (−8) for each constant change in time. A relationship is exponential if the same number is multiplied for each constant change in time.
Things to remember:
A relationship between two variables is:
- linear if the same number is added to each value to get the next value (the difference between consecutive values is constant).
- exponential if the same number is multiplied by each value to get the next value (the ratio of consecutive values is constant).
Question
Angle P has a measure of radians. If the measure of angle Q is radians greater than the measure of angle P, what is the measure of angle Q, in degrees?
| A. 30 | |
| B. 105 | |
| C. 135 | |
| D. 240 |
Hint :
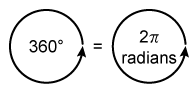
The angle measure of a complete circle is 360°, or 2π radians.
For any angle, the ratio of its degree measure to 360° must equal the ratio of its radian measure to 2π radians.
Explanation
An angle can be measured in radians or degrees. A complete circle contains 2π radians, or 360°.
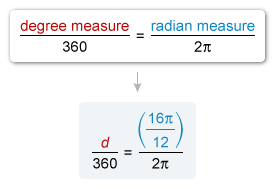
It is given that the measure of angle Q is radians greater than that of angle P, and that the measure of angle P is radians. Add to find the radian measure of angle Q.
To add fractions, first rewrite them with a common denominator.
The radian measure of angle Q is radians. Let d be the equivalent degree measure and set up a proportion.
For any angle, the ratio of the degree measure to 360° must equal the ratio of the radian measure to 2π radians. Plug in the given radian measures and then solve the proportion.
Now solve for d.
The measure of angle Q is 240 degrees.
Note: It is also possible to first find the degree measure for each angle, and then add 105 and 135 to find that the degree measure of angle Q is 240.
(Choice A) 30 may result from finding the degree measure that is 3π4 radians less than (instead of greater than) the measure of angle P.
(Choice B) 105 is the degree measure that is equivalent to 7π12 radians, but angle Q is 3π4 radians greater than 7π12 radians.
(Choice C) 135 is the degree measure that is equivalent to 3π4 radians, but angle Q is 3π4 radians greater than 7π12 radians.
Things to remember:
The ratio of the degree measure of an angle to 360° must be equal to the ratio of the radian measure of the same angle to 2π radians.
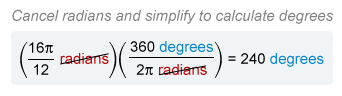
To convert from radians to degrees, it is also possible to multiply by a conversion factor that cancels the old unit and replaces it with the new unit.
A conversion factor is a fraction that is equivalent to 1, so it changes only the units and not the quantity. Use a fraction with the new unit in the numerator and the old unit in the denominator.
The radian measure of angle Q is (see main explanation). To convert from radians to degrees, multiply by a fraction with degrees in the numerator and the equivalent number of radians in the denominator.
The conversion is 360° = 2π radians, so the conversion factor is . Cancel radians and simplify to find that radians is equivalent to 240 degrees.
The measure of angle Q is 240 degrees.
Note: It is possible to use an equivalent conversion 180° = π radians when converting between degrees and radians.
Things to remember:
- To convert from one unit to another, multiply by a conversion factor that cancels the old unit and replaces it with the new unit.
- The conversion between degrees and radians is 360° = 2π radians or 180° = π radians.
SAT Math Geometry and Trigonometry Example Questions
Question
In the system of equations shown, r is a constant. If the system has no solution, what is the value of r?
A system of linear equations has no solution if the same expression of x and y is equal to two different numbers.
Explanation
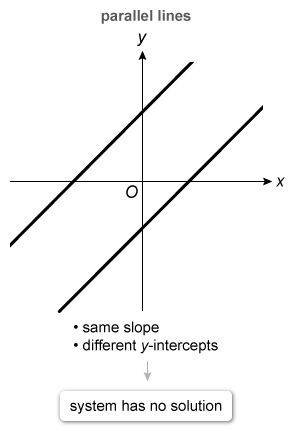
It is given that the system has no solution, so its graph must consist of lines that do not intersect. Therefore, the lines must be parallel. Parallel lines have the same slope but different y-intercepts.
Rewrite the given system of linear equations in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept. Isolate the y-term in the first equation.
Rewrite the second equation to align like terms, then compare the two equations to identify the slopes and y-intercepts.
Set the slopes equal and solve for r to find the value of r that makes the slopes the same.
| Set slopes equal | |
| Multiply both sides by r | |
| Multiply both sides by , the reciprocal of | |
| Simplify |
For the y-intercepts to be different and the slopes to be the same, the value of r must be .
Note: It is possible to plug into the second equation to verify that the y-intercepts are different (graph).
Things to remember:
- A system of linear equations has no solution if its graph consists of two parallel lines because parallel lines never intersect.
- Parallel lines have the same slope but different y-intercepts.
Alternate Method :
A system has no solution if the same expression of x and y is equal to two different numbers.
Rewrite the given system of linear equations in standard form so that the constant terms are isolated.
Now each equation is written in standard form. Notice that is a multiple of . Multiply the first equation by 2 so that the x-terms are the same and .
The x-terms are the same and and the constant terms are different , so identify the value of r that makes the y-terms the same.
Therefore, the value of r must be for the system to have no solution.
Things to remember:
A system has no solution if the same expression of x and y is equal to two different numbers.
Question
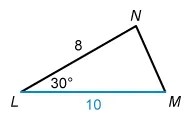
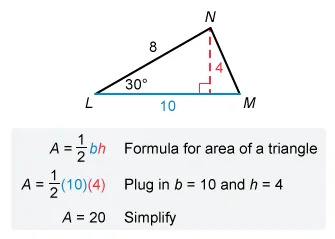
In triangle LMN, the measure of angle is 30°, the length of is 10 units and the length of is 8 units. What is the area, in square units, of triangle ?
The height of a triangle is the perpendicular distance from the base of the triangle to the opposite vertex.
Explanation
The formula for the area of a triangle is , where b is the length of the base and h is the height.
Draw triangle LMN and label it with the given information. Let with a given length of 10 be the base of the triangle and notice the height of the triangle is unknown.
The height of a triangle is the perpendicular distance from the base of the triangle to the opposite vertex.
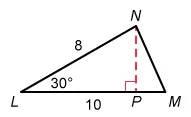
Draw a line segment from vertex N down and perpendicular to base . Label the new point of intersection P. The length of is the height of triangle LMN.
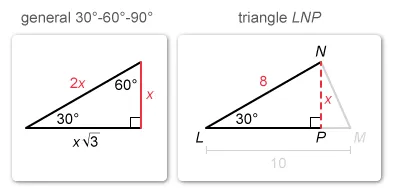
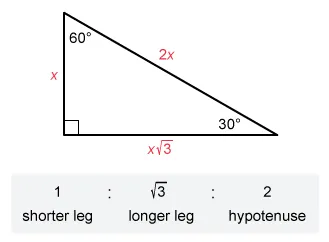
Triangle LNP is a right triangle with a given angle of 30°, so it is a 30°-60°-90° triangle.
In a 30°-60°-90° triangle, the hypotenuse is twice the length of the shorter leg. Compare the side lengths of the general triangle to triangle LNP to see that hypotenuse must be twice the height .
The length of the hypotenuse is 8, so set and divide by 2 to find the length of the shorter leg x.
| Length of hypotenuse of special right triangle | |
| Divide by 2 on both sides |
The length of the shorter leg is 4, so the height of triangle LMN is 4. Plug the length of the base (10) and the height (4) into the formula for the area of a triangle and simplify.
The area of triangle LMN, in square units, is .
Things to remember:
- The formula for the area of a triangle is , where b is the length of the base and h is the height.
- A 30°-60°-90° triangle has the following ratio of side lengths:
- The height of a triangle is the perpendicular distance from the base of the triangle to the opposite vertex.
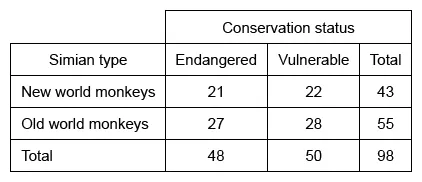
Question
The table above shows a number of species of simians classified by type and conservation status. What is the ratio of vulnerable New World monkeys to endangered New World monkeys?
| A. 21 : 22 | |
| B. 22 : 21 | |
| C. 27 : 28 | |
| D.28 : 27 |
Hint :
Identify the number of monkeys from the table that are in each category.
Explanation
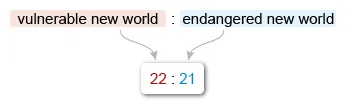
A ratio is a comparison of numbers. To find the ratio of vulnerable New World monkeys to endangered New World monkeys, identify the number of each from the table.
Identify the intersection of the Vulnerable column and the New World row.
Identify the intersection of the Endangered column and the New World row.
The choices are given in odds form, so the ratio of vulnerable New World monkeys to endangered New World monkeys is 22 : 21.
(Choice A) 21 : 22 may result from mistakenly swapping the order of the numbers in the desired ratio.
(Choice C) 27 : 28 may result from the errors described in Choices A and D.
(Choice D) 28 : 27 may result from mistakenly identifying the numbers in the Old World row (instead of the New World row).
Things to remember:
A ratio is a comparison of numbers. It is possible to express a ratio in the following forms:
SAT Math Grid-In Sample Questions
Question
| y = −x 2 + 4x + p |
| y = −6 |
In the system of equations shown, p is a constant. For which value of p does the system have exactly one distinct real solution?
A solution to a system of equations is a point of intersection (x, y) in the xy-plane. In the given system, y = −6 represents a horizontal line and y = −x 2 + 4x + p represents a parabola.
Explanation
A solution to a system of equations is a point of intersection (x, y) in the xy-plane. In the given system, y = −6 represents a horizontal line and y = −x 2 + 4x + p represents a parabola.
A parabola intersects a horizontal line at 0, 1, or 2 points. If a parabola intersects a horizontal line at a single point, then that point must be the vertex of the parabola (proof).
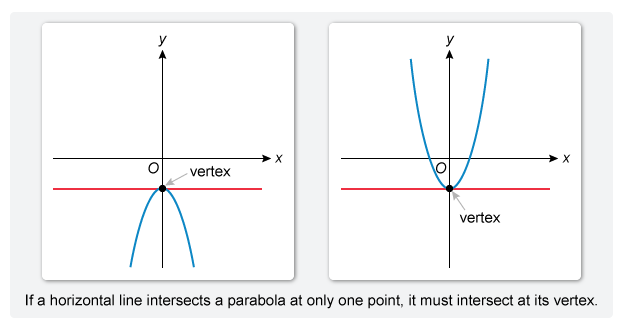
To find the value of p, first find the coordinates of the vertex of the parabola. Use the vertex formula for an equation in standard form y = ax 2 + bx + c to find the x-coordinate of the vertex.

Compare the equation of the parabola y = −x 2 + 4x + p to standard form y = ax 2 + bx + c to see that a = −1 and b = 4. Plug these values into the vertex formula and simplify.
| x-coordinate of vertex | |
| Plug in a = −1 and b = 4 | |
| x=2 | Simplify |
The x-coordinate of the vertex is 2. The parabola intersects the line y = −6 when the y-coordinate of the vertex is equal to −6.
Therefore, the given system of equations has exactly one distinct real solution when the vertex of the parabola is (2, −6). Plug (x, y) = (2, −6) into the equation y = −x 2 + 4x + p and solve for p.
| y = −x2 + 4x + p | Given equation |
| −6 = −(2)2 + 4(2) + p | Plug in (x, y) = (2, −6) |
| −6 = −4 + 8 + p | Apply exponent and multiply |
| −6 = 4 + p | Combine constant terms |
| −10 = p | Subtract 4 from both sides |
Things to remember:
- A solution to a system of equations is a point where the graphs of the equations intersect in the xy-plane.
- If a horizontal line intersects a parabola at only one point, it must intersect at the vertex of the parabola.
- The vertex formula defines the x-coordinate of the vertex of a parabola with a quadratic equation in standard form y = ax 2 + bx + c:
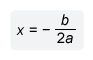
It is also possible to use the substitution method to create a single quadratic equation in terms of , then use the discriminant to determine what value of results in one distinct real solution.
It is given that , so substitute −6 for in the first equation and rewrite it in standard form .
| Given first equation | |
| Plug in | |
| Add 6 on both sides |
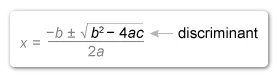
A quadratic equation in standard form has exactly one solution when the discriminant is equal to 0. The discriminant is the expression under the square root in the quadratic formula.
Compare the equation
to standard form to identify the values of
,
, and
.
Note: It is given that p is a constant, so p + 6 is also a constant.
Plug these values into the discriminant and simplify.
| b2 − 4ac | Discriminant |
| 42 − 4(−1)(p + 6) | Plug in , , and |
| Apply the exponent and simplify | |
| Distribute 4 to () | |
| Combine like terms |
The discriminant is , so the system has exactly one solution when . Set the discriminant equal to 0 and solve for .
| Set discriminant equal to 0 | |
| Subtract 40 from both sides | |
| Divide by 4 on both sides |
Things to remember:
- To find the number of solutions to a linear and quadratic system, use the substitution method to create a single equation in terms of only .
- A quadratic equation in standard form has exactly one solution when the discriminant is equal to 0.
Question
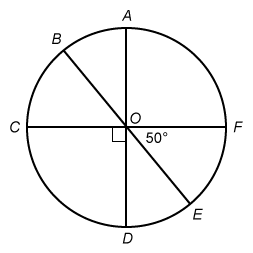
The circle shown has center , diameters , , and , and the length of is . If the length of minor arc is , what is the value of ?
The length of an arc divided by the circumference of the circle must equal the measure of its intercepting central angle divided by the measure of the entire circle.
Explanation
Ratios of the part to the whole are equivalent between the length of a circular arc and the measure of its intercepting central angle.
The length of an arc (part) divided by the circumference of the entire circle (whole) must equal the measure of its intercepting central angle (part) divided by the measure of the entire circle (whole), forming the following proportion:
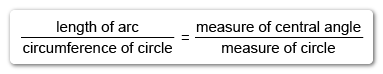
The formula for the circumference of a circle is , where is the length of the radius. The angle measure on the given figure is in degrees, so use for the measure of a whole circle (instead of radians).
The central angle that intercepts is , so write the proportion as follows:
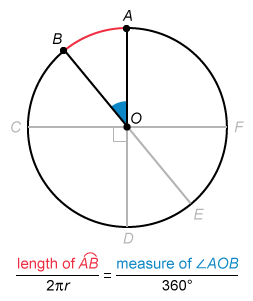
To find the measure of , first identify that and are a pair of vertical angles. When two lines intersect, the vertical angles formed by those lines are congruent.
Therefore, also has a measure of . Now notice that forms a straight line when combined with and .
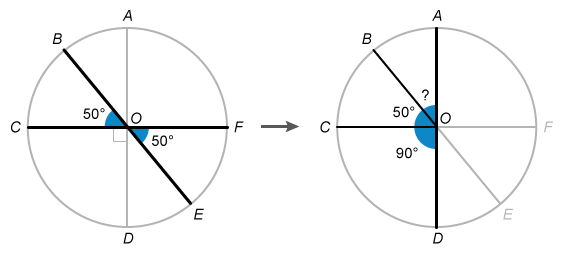
The measure of is . Notice that is a radius of the circle and has a given length of . Plug and into the proportion, and then solve for the length of .

The length of is , so the value of is 2.
Things to remember:
- Ratios of the part to the whole are equivalent between the area of a circular sector and the measure of its intercepting central angle. The following proportion relates circular sectors and central angles of a circle:
- The formula for the circumference of a circle is , where is the length of the radius.
Question
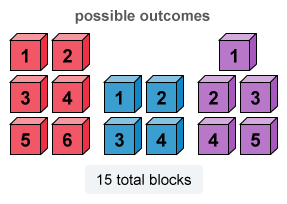
Russell's toy box contains 15 solid-colored blocks: 6 red blocks, 4 blue blocks, and 5 purple blocks. There is also a single number printed on each block. Each number from 1 through 6 is printed on a red block, each number from 1 through 4 is printed on a blue block, and each number from 1 through 5 is printed on a purple block. If Russell chooses a block at random from his toy box, what is the probability that the block will be purple or will have a 3 printed on it?
To find the probability of a desired event, use the following formula:
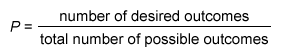
Explanation
An item with one quality OR another quality has at least one of the qualities. To find the probability of a desired event, divide the number of desired outcomes by the total number of possible outcomes.
The number of desired outcomes is the number of blocks that are purple OR printed with a 3.
The number of possible outcomes is the total number of blocks in the toy box.
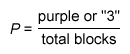
It is given that there are 15 total blocks in the toy box: 6 red blocks printed with 1 through 6, 4 blue blocks printed with 1 through 4, and 5 purple blocks printed with 1 through 5.
There are 5 purple blocks, and there are 3 blocks printed with a 3. Add 3 and 5, then subtract 1 for the 1 block that is both purple and printed with a 3 to see that there 7 blocks that are purple or printed with a 3.
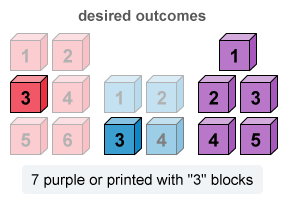
Note: There is 1 block that is both purple and printed with a 3, so it is necessary to subtract 1 from the sum of the 5 purple blocks and 3 blocks printed with a 3 to avoid double-counting.
Of the 15 total blocks, there are 7 blocks that are purple or printed with a 3.

The probability that Russell chooses a block that is purple or printed with a 3 is
Things to remember:
- To find the probability of a desired event, use the following formula:
- An item that has one quality OR another quality has at least one of the qualities (possibly both).
Your Way to a Higher SAT Math Score
The SAT Math section tests your skills in algebra, advanced math, data analysis, geometry, and trigonometry. Explore each area through our SAT Math questions, crafted by UWorld’s math educators with clear explanations that match real exam expectations.
Learn by Doing
Create Custom Quizzes
Understand the Why
Simulate Exam Conditions
Turn Weaknesses into Strengths
Replicate the Exam Environment
Students Love Our SAT Questions
Great SAT explanations which can't be found elsewhere.
Really satisfied with the quality of the math questions. They are similar to the SAT questions.
I've been using uworld for a few months now and their math section is amazing! I've improved drastically by at least 300+ points on the SAT section.
Choose Your Subscription
Get 1,650+ SAT practice questions with answers you can access anytime, anywhere, so your confidence (and your score) skyrocket.
| Save Big, Score High! | ||
| What's Included | ||
| Hone your skills with questions modeled directly after the official SAT. Each problem comes with an in-depth, visual explanation to clarify the answer and the strategy. | ||
| Build practice tests focused on YOUR weak topics. Create timed mock exams or quick topic quizzes. Study your way, not someone else's way. | ||
| See exactly which topics you're nailing and which need more work. Track your progress across all SAT practice tests and quizzes so you know where to focus. | ||
| Stop wasting time on content you already know. Choose specific SAT topics to practice and build a study plan that actually makes sense for you. | ||
| Tell us your schedule and we'll create a personalized SAT study plan that fits your life. Stay on track without the stress of figuring out what to study next. | ||
| Take a complete practice exam under real testing conditions and get an estimated SAT score. See where you stand before test day. | ||
| In-house SAT tutors and educators break down tough concepts with clear animations and step-by-step explanations. Finally, understand the topics that confuse you. | ||
| Our comprehensive SAT prep book set, available in both print and digital formats, provides focused content review. It's perfectly aligned with the videos and practice questions. | ||
| After each SAT lesson, use these foundational questions to confirm you understand the core concepts before tackling more difficult, exam-style problems. Build your confidence. | ||
| The printed SAT guide includes an additional set of unique, exam-level practice questions not found online, complete with detailed, illustrated solutions for extra practice. |
- Hone your skills with questions modeled directly after the official SAT. Each problem comes with an in-depth, visual explanation to clarify the answer and the strategy.
- Build practice tests focused on YOUR weak topics. Create timed mock exams or quick topic quizzes. Study your way, not someone else's way.
- See exactly which topics you're nailing and which need more work. Track your progress across all SAT practice tests and quizzes so you know where to focus.
- Stop wasting time on content you already know. Choose specific SAT topics to practice and build a study plan that actually makes sense for you.
- Tell us your schedule and we'll create a personalized SAT study plan that fits your life. Stay on track without the stress of figuring out what to study next.
- Take a complete practice exam under real testing conditions and get an estimated SAT score. See where you stand before test day.
- Hone your skills with questions modeled directly after the official SAT. Each problem comes with an in-depth, visual explanation to clarify the answer and the strategy.
- Build practice tests focused on YOUR weak topics. Create timed mock exams or quick topic quizzes. Study your way, not someone else's way.
- See exactly which topics you're nailing and which need more work. Track your progress across all SAT practice tests and quizzes so you know where to focus.
- Stop wasting time on content you already know. Choose specific SAT topics to practice and build a study plan that actually makes sense for you.
- Tell us your schedule and we'll create a personalized SAT study plan that fits your life. Stay on track without the stress of figuring out what to study next.
- Take a complete practice exam under real testing conditions and get an estimated SAT score. See where you stand before test day.
- In-house SAT tutors and educators break down tough concepts with clear animations and step-by-step explanations. Finally, understand the topics that confuse you.
- Our comprehensive SAT prep book set, available in both print and digital formats, provides focused content review. It's perfectly aligned with the videos and practice questions.
- After each SAT lesson, use these foundational questions to confirm you understand the core concepts before tackling more difficult, exam-style problems. Build your confidence.
- The printed SAT guide includes an additional set of unique, exam-level practice questions not found online, complete with detailed, illustrated solutions for extra practice.
Try free SAT sample questions today! Whether you need a quick math boost or want to dive deep into the full test, your trial’s got you covered.
Stay Sharp with UWorld’s SAT Math Question of the Week
Meet Our Expert SAT Teachers

27 years teaching high school English, including 16 years for AP® English Language
Advanced rhetorical analysis, argumentative writing, and college-level literary skills
Creates study materials for the SAT and ACT exams

37 years teaching high school English, including 23 years for AP English Literature
In-depth knowledge of literature, language, and skills needed for academic success
Has a Bachelor of Arts in English and a master’s in Humanities; creates study materials for the SAT and ACT exams


25+ years tutoring students for the SAT and ACT®, and 10 years as an SAT essay grader for the College Board®
High-school English, GED classes, and college-level composition classes
Has a Bachelor of Arts in English with a specialization in Creative Writing and a Master of Arts in English as a Second Language


13 years tutoring high-school students in English and math
SAT and ACT preparation, testing strategies, and a focus on helping students strengthen their academic foundation
Creates study materials for both the SAT and ACT exams


22 years in math education — classrooms and educational tech startups
Pedagogy and addressing students’ needs in math through traditional and innovative solutions
Has a Bachelor of Science in Applied Mathematical Sciences and a Master of Arts in Mathematics


10 years in engineering, and 12 years teaching high-school math
Technical and instructional disciplines by applying math to the SAT and ACT in preparation for future technical studies
Has a Bachelor of Science in Mechanical Engineering and Master of Science in Engineering


20 years in math education, ranging from Algebra I to AP Calculus, and curriculum writing at both district and state levels
Pedagogy with real-world testing standards to prepare students for the SAT, ACT, AP Calculus, and AP Statistics
Has a master's in Education and has completed doctoral coursework


10+ years in SAT/ACT math content development, and 4 years teaching underperforming students
Adaptable and diverse math teaching methods that help students across skill levels
Has a dual degree in Philosophy and Mathematics

Awards & Recognition

2023 EdTech Awards Cool Tool Finalist

Tech & Learning Awards of Excellence Best of 2022

The Tech Edvocate Awards 2022

Parent and Teacher Choice Award

2022 EdTech Awards Cool Tool Finalist
Frequently Asked Questions (FAQs)
What are SAT Math sample questions?
SAT Math sample questions are real-style math examples that mirror the logic, structure, and problem-solving skills tested on the official SAT exam. These sample SAT Math problems cover a range of topics, including algebra, geometry, data analysis, and advanced math concepts. They help students understand what to expect on test day while giving parents insight into the level of difficulty their child will face.
Practicing with SAT test sample math questions enables students to develop familiarity, build confidence, and improve accuracy, ultimately making them better prepared for the real exam.
Are these SAT Math sample questions similar to real exam questions?
Yes! UWorld’s SAT Math sample test content is carefully designed to match the format, question style, and difficulty of the actual SAT. Each sample SAT Math test question reflects the reasoning, logic, and concepts found in the real exam.
By practicing with these SAT sample math questions, students learn how to interpret question wording, identify patterns, and apply math concepts efficiently. This builds confidence and ensures that their preparation feels just like the real test.
Do the SAT Math sample questions include answers and explanations?
Absolutely. Every SAT Math sample question comes with a step-by-step solution and a detailed explanation. Students can review SAT Math sample questions and answers to understand why an answer is correct, not just what the answer is.
Each explanation helps students identify the best solving strategies, recall key formulas, and avoid common mistakes. These sample SAT Math questions with answers make studying interactive, meaningful, and easy to follow.
Can I download SAT Math sample questions as a PDF?
Currently, UWorld does not offer a SAT Math sample test PDF or SAT Math sample questions PDF for download. Instead, students can access all SAT Math examples online in UWorld’s interactive learning platform.
This digital approach allows students to:
- Solve problems instantly and check answers in real time
- Review detailed explanations for every question
- Access their sample SAT Math tests anytime, anywhere
It’s convenient, eco-friendly, and designed to support active learning.
What types of SAT Math example problems are available?
UWorld’s SAT Math example problems cover all major math domains included in the official SAT:
- Algebra: Linear equations, inequalities, and systems of equations
- Data Analysis: Ratios, percentages, and probabilities
- Advanced Math: Quadratic, polynomial, and exponential functions
- Geometry & Trigonometry: Angles, coordinate geometry, and measurement formulas
These sample SAT Math problems help students strengthen conceptual understanding, sharpen problem-solving speed, and boost overall test performance.
Are there sample SAT geometry questions?
Yes! Students can access plenty of sample SAT geometry questions within UWorld’s practice platform. These focus on circles, triangles, angles, and coordinate geometry, as well as trigonometric ratios.
Each SAT Math sample problem in the geometry section includes visuals, explanations, and formula breakdowns. Students learn not just how to solve, but how to visualize and apply geometry concepts effectively.
What’s the difference between SAT Math sample problems and example questions?
Both SAT Math sample problems and example SAT Math questions reflect real SAT-style items, but they serve slightly different purposes:
- Sample problems simulate multi-step, higher-difficulty scenarios that test reasoning and time management.
- Example questions focus on single concepts or skill applications.
Using both gives students balanced exposure to the variety of question types they’ll see on the SAT sample paper maths or actual SAT Math section.
Are SAT Math Level 1 and Level 2 sample questions included?
Yes. UWorld’s practice materials include both SAT II Math sample tests, commonly known as SAT Math Level 1 and SAT Math Level 2 sample tests.
- Level 1 covers algebra, geometry, and data analysis.
- Level 2 includes higher-level topics like trigonometry, advanced functions, and coordinate geometry.
Both levels of SAT Math 2 sample tests are available online, ensuring students are prepared for all types of questions. (Note: These reflect the style of older Subject Tests but remain useful for deeper practice.)
How can SAT Math sample problems help improve scores?
Working through realistic SAT Math sample tests helps students strengthen accuracy, timing, and conceptual mastery.
Here’s how:
- Practice builds familiarity: Students recognize question patterns and avoid surprises.
- Explanations build understanding: Reviewing sample SAT Math questions with answers helps them learn why answers are right or wrong.
- Timed practice improves pacing: Simulated SAT Math sample tests teach students to manage time effectively.
Consistent practice with SAT Math sample problems leads to measurable score improvement, and greater confidence on test day.
How do UWorld’s SAT Math examples compare to other resources?
UWorld’s sample SAT Math tests stand out for their realism and detailed explanations. Unlike generic worksheets or PDFs, our SAT Math example questions mimic the official SAT structure exactly.
Students don’t just practice, they learn how to think like the test maker. That’s why UWorld is trusted by students, parents, and educators nationwide for SAT preparation.