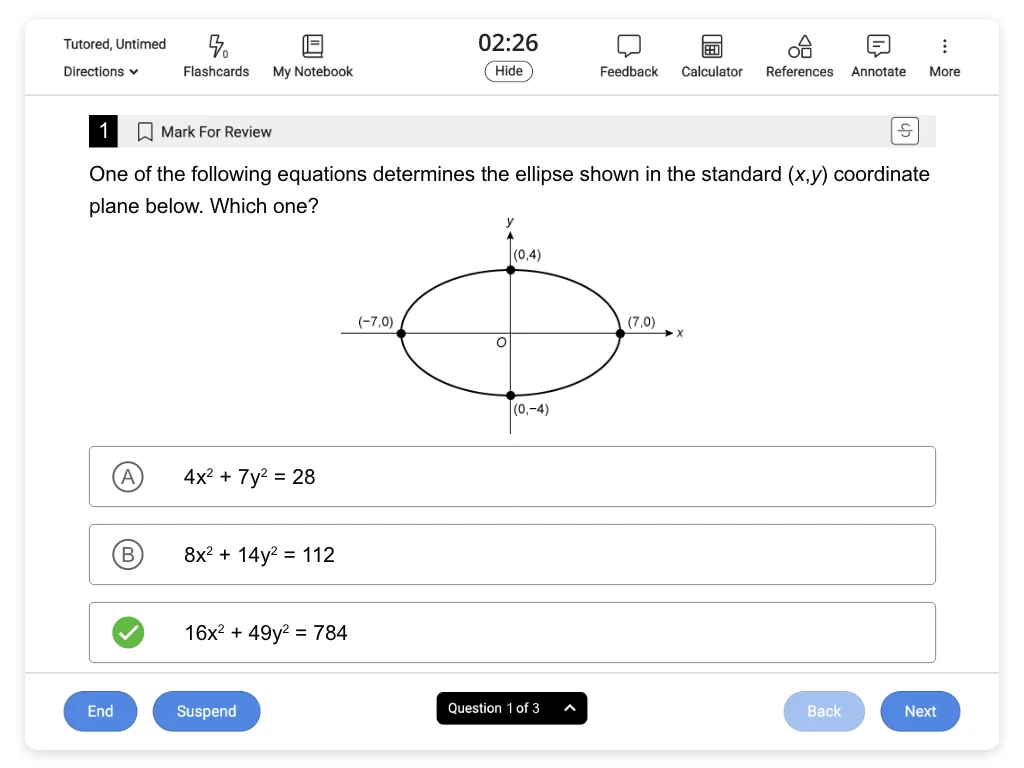
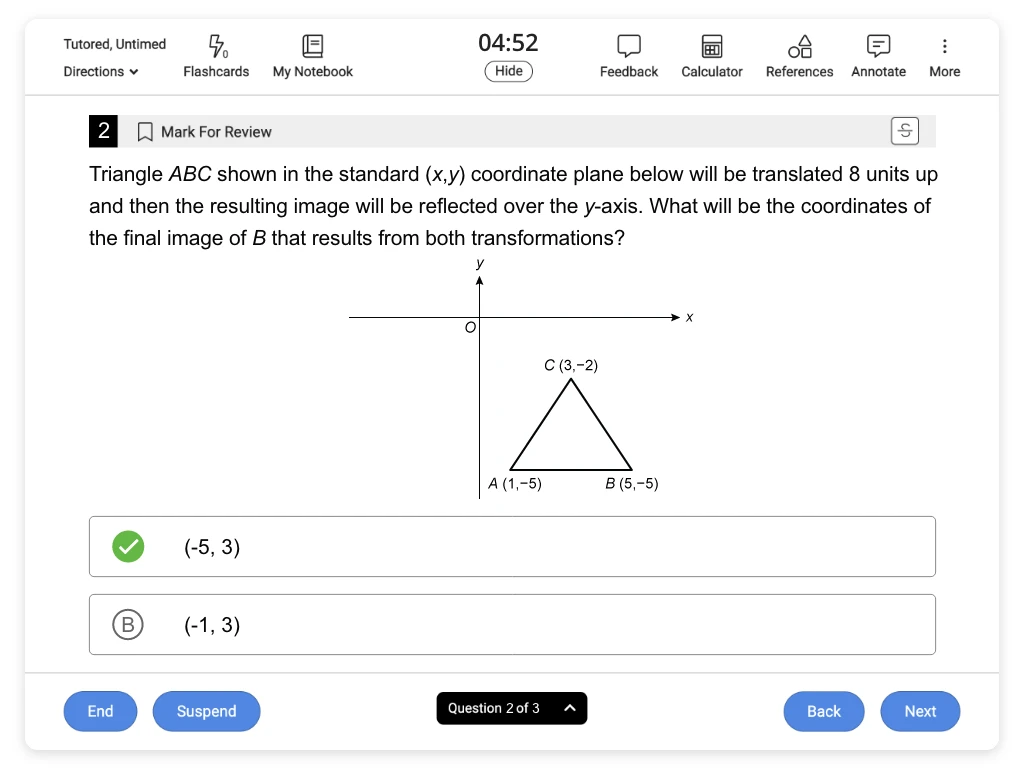
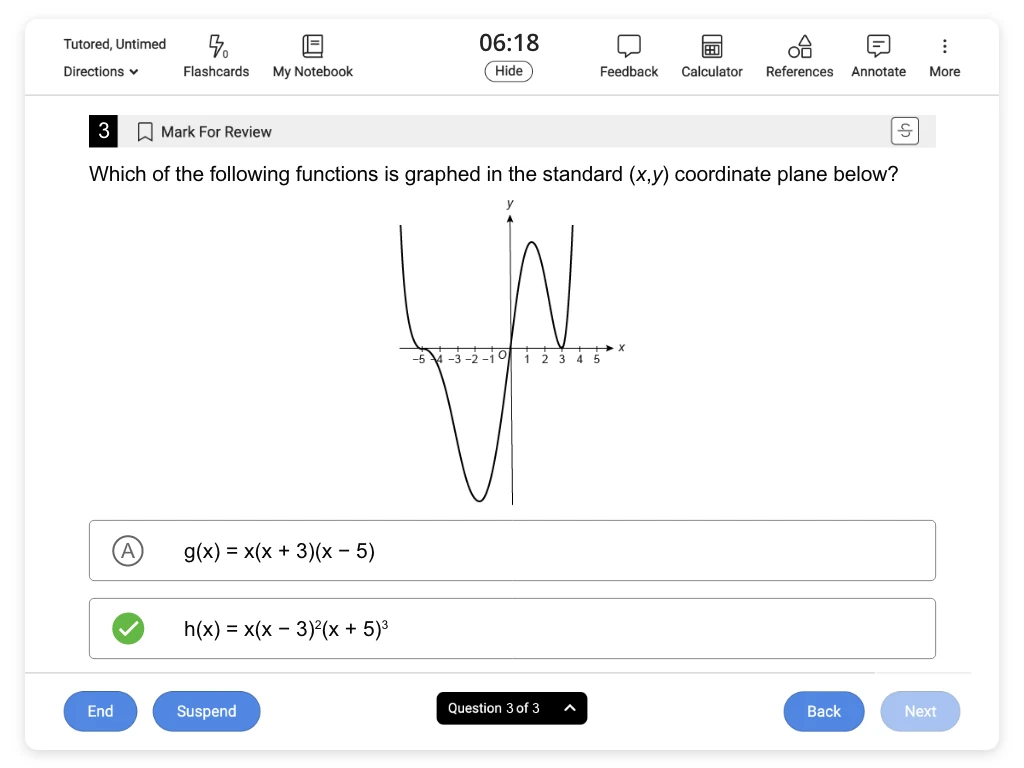
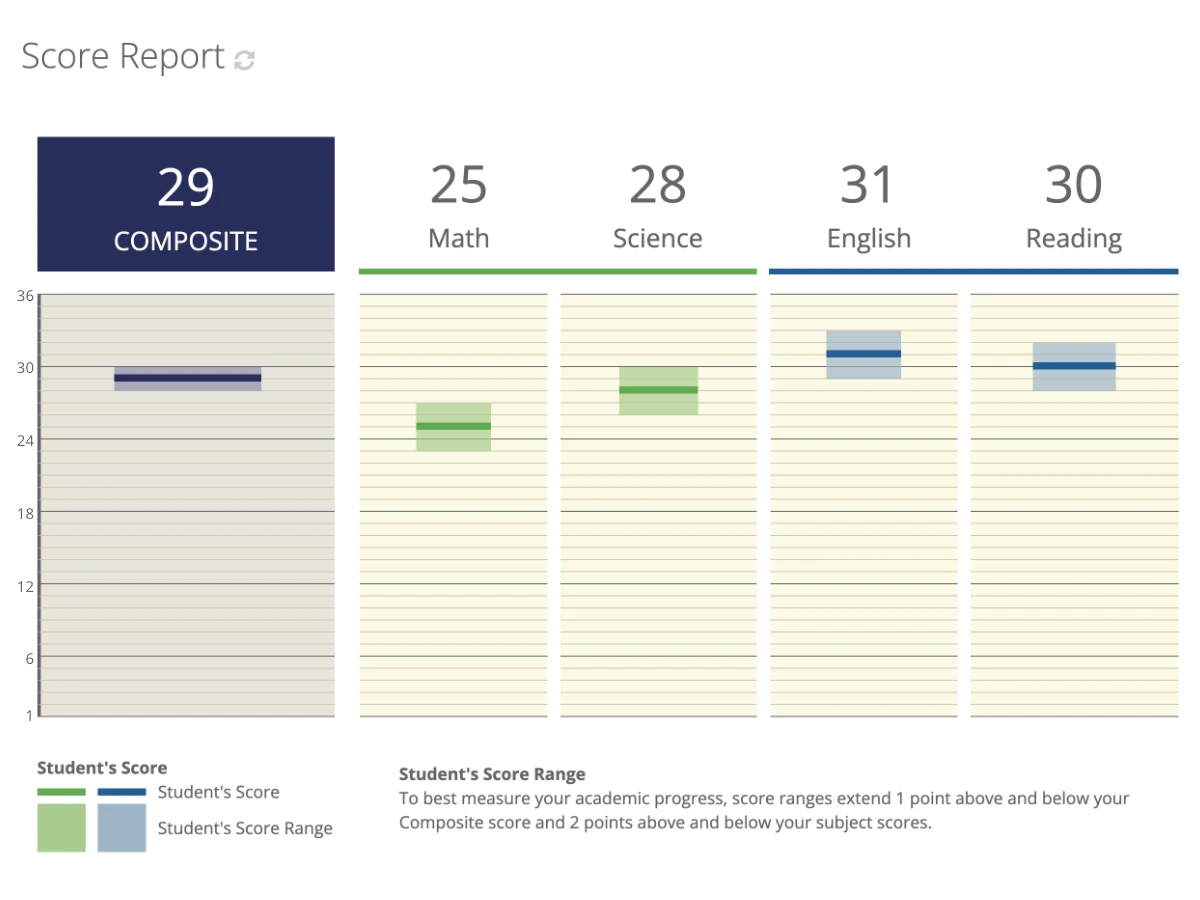
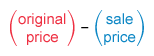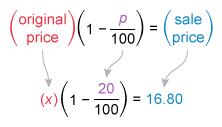ACT® Math Practice Tests and Questions
Our Practice Tests and Questions for ACT® Math are expertly designed to match or surpass the difficulty level of the actual exam, ensuring a realistic practice experience. With comprehensive answer explanations and vivid illustrations, we make even the most challenging concepts easily understandable.
Get Exam-Ready with Exam-Like ACT Math Practice
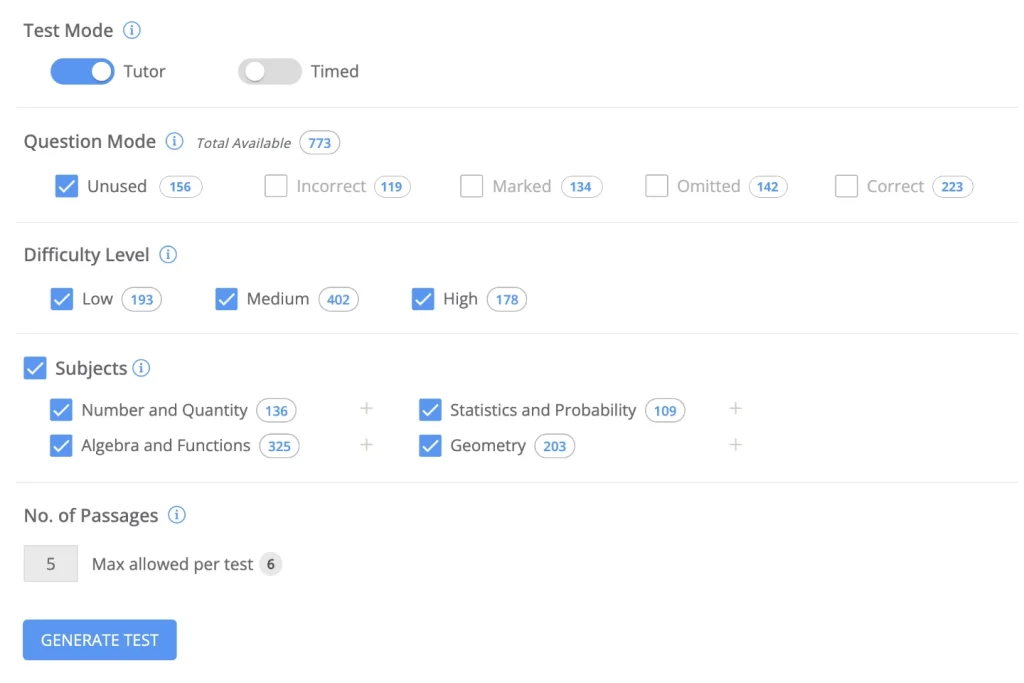
Unlimited Exam-level Practice
Customized to Your Needs
Understand the Why
ACT Math Sample Questions
Brandi bought dog food that was on sale from the Pet Store. The sale price of the food was $16.80, which was 20% off the original price. How much more was the original price than the sale price?
| A. $0.21 | |
| B. $0.84 | |
| C. $2.80 | |
| D. $3.36 | |
| E. $4.20 |
Hint: To decrease an amount by p%, multiply it by (1 ─ p / 100 )
The question asks how much more the original price is than the sale price, so find the difference of the original price and the sale price.
First calculate the original price from the given information and then subtract to find the difference.
It is given that the sale price of the dog food is 20% off the original price, so the sale price ($16.80) is the result of a 20% decrease of the original price. To decrease an amount by p%, multiply it by (1 ─ p / 100 ) (proof).
Let the original price be x and write an equation to relate the original price (x), the given percent decrease (p = 20), and the given sale price ($16.80).
Now solve the equation for x, the original price.
The original price of the dog food was $21.
Now subtract the sale price from the original price to find the difference.
Therefore, the original price was $4.20 more than the sale price.
(Choice A) $0.21 is equivalent to the sale price divided by 80 (instead of 0.80). It may result from the misconception that to calculate a p% decrease, it is necessary to multiply by (100 − p) instead of (1 ─ p / 100 ).
(Choice B) $0.84 is equivalent to the sale price divided by 20 (instead of 0.80). It may result from the misconception that to calculate a p% decrease, it is necessary to multiply by p instead of (1 ─ p / 100 ).
(Choice C) $2.80 may result from the misconception that to calculate a p% decrease, it is necessary to multiply by (1 + p / 100 ) instead of (1 ─ p / 100 ).
(Choice D) $3.36 may result from mistaking $16.80 to be the original price (instead of the sale price). This may also result from multiplying (instead of dividing) the sale price by (1 ─ 20 / 100 ).
Things to remember:
- A discounted price that is p% less than an original price is equivalent to the original price decreased by p%.
- To decrease a value by p%, multiply it by (1 ─ p / 100 ).
What real value of x satisfies the equation log2x = −3 ?
| A. −9 | |
| B. −8 | |
| C. −6 | |
| D. 1 / 6 | |
| E. 1 / 8 |
Hint: To solve a logarithmic equation, convert it to exponential form.

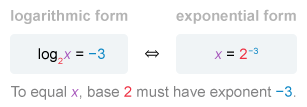
To solve the equation log2x = −3 for x, first convert the equation to exponential form.
The general equation log b x = y means that to equal x (called the argument), the base b must have the exponent y.
Convert the given equation log2x = −3 from logarithmic form to exponential form.
The given equation in exponential form is x = 2−3 . However, none of the answer choices match the form 2−3. The exponent is negative, so use the negative exponent rule to rewrite 2−3.
| x = 2−3 | Given equation in exponential form |
| x = 1 / 23 | Use the negative exponent rule: x−n = 1 / xn |
| x = 1 / 8 | Simplify in the denominator: 23 = 2 ∙ 2 ∙ 2 |
The value of x is 1 / 8 .
(Choice A) −9 may result from mistaking the value of x to be −32 (instead of 2−3) when attempting to convert the given equation to exponential form. An equation of the form log b x = y in exponential form is x = b y , where b is the base and y is the exponent.
(Choice B) −8 may result from incorrectly rewriting 2−3 as −23 (instead of 1 / 23 ).
(Choice C) −6 may result from incorrectly rewriting 2−3 as 2 ∙ (−3), instead of 1 / 23 .
(Choice D) 1 / 6 may result from incorrectly rewriting 2−3 as 1 / 2.3 (instead of 1 / 23 ).
Things to remember:
- To convert between logarithmic and exponential forms of an equation, use the relationship:

- To rewrite expressions with negative exponents, use the negative exponent rule: x−n = 1 / xn .
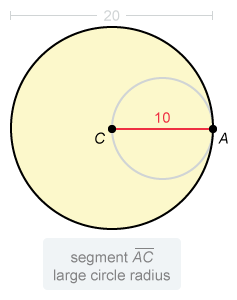
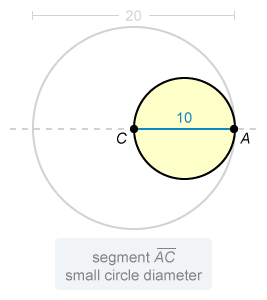
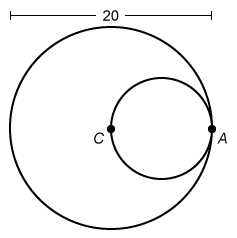
A large circle and a small circle are tangent at A, as shown in the figure below. The small circle passes through the center C of the large circle. The diameter of the large circle is 20 inches. What is the ratio of the area of the large circle to the area of the small circle?
- 2 ∶ 1
- 4 ∶ 1
- 5 ∶ 1
- 2π ∶ 1
- 4π ∶ 11
Hint : The formula for the area of a circle is A=πr 2, where r is the radius. Determine the area of each circle to find the desired ratio.
The formula for the area of a circle is A=πr 2, where r is the radius. To find the ratio of the areas, first use the given diameter of the large circle and the properties of tangent circles to find the radius of each circle.
The radius of a circle is half the diameter. The given diameter of the large circle is 20 inches, so the length of its radius is 10. Tangent point A is on the large circle, so segment AC is a radius. Draw and label AC = 10.
It is given that the circles are tangent at point A, so point A is on the small circle.
It is given that the small circle passes through the center of the large circle, so point C is on the small circle.
The point of tangency and the centers of tangent circles lie on the same line, so segment AC must pass through the center of the small circle. Therefore, AC is a diameter of the small circle.
The length of AC is 10, so the length of the diameter of the small circle is 10. The radius of a circle is half the diameter, so the length of the radius of the small circle is 5 inches.
Plug the radius of the large circle (10) and the radius of the small circle (5) into the formula for the area of a circle to find the areas of the large and the small circles.
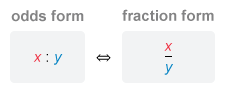
Notice that the answer choices are all in odds form x : y, which means the ratio of x to y. Therefore, the ratio of the area of the large circle to the area of the small circle is 100π ∶ 25π.
The ratio 100π ∶ 25π is not an answer choice but notice that it is reducible. To simplify a ratio in odds form, it is helpful to first rewrite it in fraction form x / y .
Now cancel common factors and then convert back to odds form (x : y) to match the answer choices.
| 100 π / 25 π | Ratio in fraction form |
| 25⋅4⋅π / 25⋅1⋅π | Cancel the greatest common factor (GCF) |
| 4 / 1 | Simplify |
| 4 : 1 | Convert to odds form |
Note: It is possible to simplify 100π ∶ 25π directly in odds form by cancelling factors common to both sides: 25π⋅ 4 ∶ 25π⋅1.
Therefore, the ratio of the area of the large circle to the area of the small circle is 4 : 1.
(Choice A) 2 : 1 may result from mistakenly using πr for the area of a circle instead of A=πr 2.
(Choices C and E) 5 : 1 and 4π ∶ 1 may result from a calculation error when simplifying the ratio of the areas.
(Choice D) 2π ∶ 1 may result from the combination of errors described in Choices A, C, and E.
Things to remember:
- The formula for the area of a circle is A=πr 2, where r is the radius.
- The ratio of x to y can be expressed in odds form x ∶ y. To simplify a ratio in odds form, it is helpful to first rewrite it in fraction form x / y .
Among the following numbers, which has the greatest value?
| A. 0.252 | |
| B. 0.25 | |
| C. 0.25 | |
| D. 250 / 999 | |
| E. 25 / 101 |
Hint : To determine which number has the greatest value, first convert the numbers to the same form (ex. fraction, decimal).
A decimal with a bar (0.1) represents a repeating decimal. The digit pattern below the bar repeats indefinitely.
To determine which number has the greatest value, first convert the numbers to the same form (ex. fraction, decimal).
It is simpler to compare the numbers as decimals, so convert the fractions 250 / 999 and 25 / 101 to decimal form. To convert a fraction to a decimal, divide the numerator by the denominator.
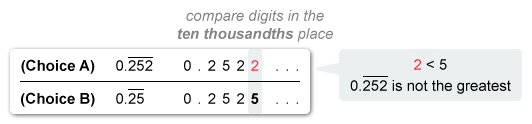
Any decimal with a bar represents a repeating decimal. The digit pattern below the bar repeats indefinitely so rewrite 0.252 and 0.25 as repeating decimals.
Now compare the place values of each decimal number. Start with the highest place value (first digit to the left). If two or more numbers have the same digit in the highest place, compare the digits in the next highest place.
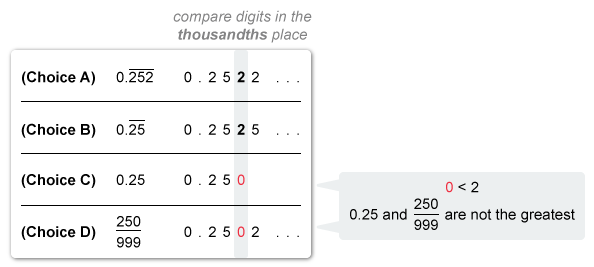
Each of the numbers in decimal form have the same digit (0) in the ones place and the same digit (2) in the tenths place, so compare each digit in the hundredths place.
Eliminate Choice E because 25 / 101 does not have the greatest value. Now compare each digit in the thousandths place of the remaining numbers.
Note: It is possible to add zeros after the rightmost given place of a decimal number without changing its value. Write 0.25 as 0.250 so that it has a digit in the thousandths place.
Eliminate Choices C and D because 0.25 and 250 / 999 do not have the greatest value.
Now compare each digit in the ten thousandths place of the remaining two numbers 0.25 and 0.252
Eliminate Choice A because 252 does not have the greatest value.
By process of elimination, 0.25 has the greatest value.
Things to remember:
- To compare the value of numbers in different forms, convert the numbers to the same form (ex. fraction, decimal).
- A decimal with a bar represents a repeating decimal. The digit pattern below the bar repeats indefinitely.
Line l is shown in the standard (x,y) coordinate plane below. Line n has a slope that is 4 times the slope of line l and a y-intercept that is 1 / 2 of the y-intercept of line l. Line n has which of the following equations?
| A. y = 1 / 2 x + 1 | |
| B. y = ─ 1 / 2 x + 1 | |
| C. y = ─ x + 6 | |
| D. y = 4x + 3 | |
| E. y = ─4x + 3 |
Hint : Find the slope and y-intercept of the given graph of line l, and then use the given information to write an equation for line n in slope-intercept form y = mx + b.
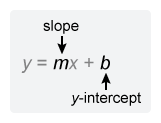
Notice that each choice is an equation in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
Find the slope and y-intercept of the given graph of line l, and then use the given information to write an equation for line n in slope-intercept form.
slope of line l
The slope of a line is equal to rise / run , where the “rise” is the vertical distance between any two points and the “run” is the horizontal distance between the same two points.
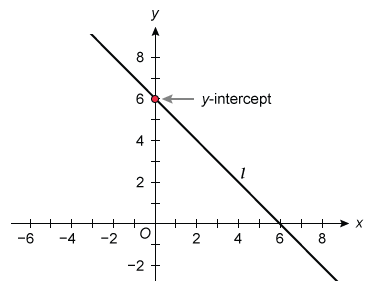
To find the slope of line l, identify the coordinates of any two points on the line and divide the rise by the run. Choose the points (0, 6) and (6, 0), where the line crosses the y-axis and x-axis.
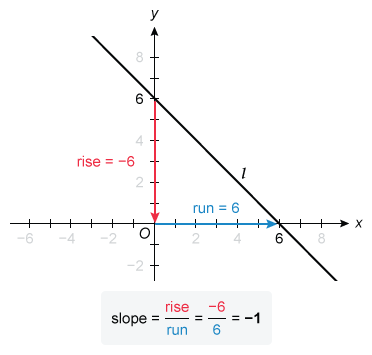
The slope of line l is -1.
y-intercept of line l
The y-intercept of a line is the value of y when x = 0. The graph of line l passes through the point (0, 6), so the y-intercept of line l is 6.
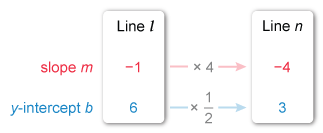
The slope of line l is −1 and the y-intercept is 6.
It is given that line n has a slope 4 times that of line l and a y-intercept 1 / 2 that of line l , so multiply the slope of line l by 4 and multiply the y-intercept of line l by 1 / 2 to find the corresponding values of line n.
Plug m = −4 and b = 3 into slope-intercept form y = mx + b to write an equation for line n
Therefore, the equation of line n is y = −4x + 3.
(Choice A) y = 1 / 2 x + 1 may result from a combination of the errors described in Choices B and D.
(Choice B)y = – 1 / 2 x + 1 is an equation of a line with a slope that is 1 / 2 the slope (instead of 4 times the slope) of line l and a y-intercept that is 1 / 6 the y-intercept (instead of 1 / 2 the y-intercept) of line l.
(Choice C) y = –x + 6 is the equation of line l, but the question asks for the equation of line n.
(Choice D) y = 4x + 3 may result from mistaking the slope of line l to be 1 (instead of −1). However, a line that decreases vertically as values on the horizontal axis increase has a negative slope.
Things to remember:
- The slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept.
- The slope of a line is equal to rise / run , where the “rise” is the vertical distance between any two points and the “run” is the horizontal distance between the same two points.
Score Free ACT Questions Every Week!
Get ACT exam-ready with weekly exam-like questions sent to your inbox.
Get a 36 on ACT Math Section with UWorld
Study content crafted by subject matter experts, assess yourself with exam-level practice, measure your performance, target your weaknesses with focused study, and repeat.
"UWorld's question bank can be described in one word: revolutionary. It accurately models the content that you would see on the test and familiarizes you with the test through PRACTICE, not mindless reading of the content. After using UWorld's amazing question bank, I was able to score a 36. It's proven to work and yielded amazingly good results for me!"
- Ravi
Create Unlimited Practice Tests with Exam-Level Questions
- What if you could take the ACT Math as many times as you needed before it actually counted? Well, you can.
- Study formulas and hone your computational skills with as many practice tests as you need using hundreds of exam-level questions.
- Customize by topic, custom tag, or even just questions you’ve previously gotten wrong.
Create Unlimited Practice Tests with Exam-Level Questions
- What if you could take the ACT Math as many times as you needed before it actually counted? Well, you can.
- Study formulas and hone your computational skills with as many practice tests as you need using hundreds of exam-level questions.
- Customize by topic, custom tag, or even just questions you’ve previously gotten wrong.
Understand Why an Answer is Right or Wrong
- Embracing the challenge of understanding complex mathematical formulas leads to great rewards. That's why we offer comprehensive explanations for each answer choice, along with visually engaging charts, graphs, and illustrations that unravel the intricacies, making them more accessible to grasp.
- Plus, you can import QBank content to your customizable digital flashcards and review it anytime.
Understand Why an Answer is Right or Wrong
- Embracing the challenge of understanding complex mathematical formulas leads to great rewards. That's why we offer comprehensive explanations for each answer choice, along with visually engaging charts, graphs, and illustrations that unravel the intricacies, making them more accessible to grasp.
- Plus, you can import QBank content to your customizable digital flashcards and review it anytime.
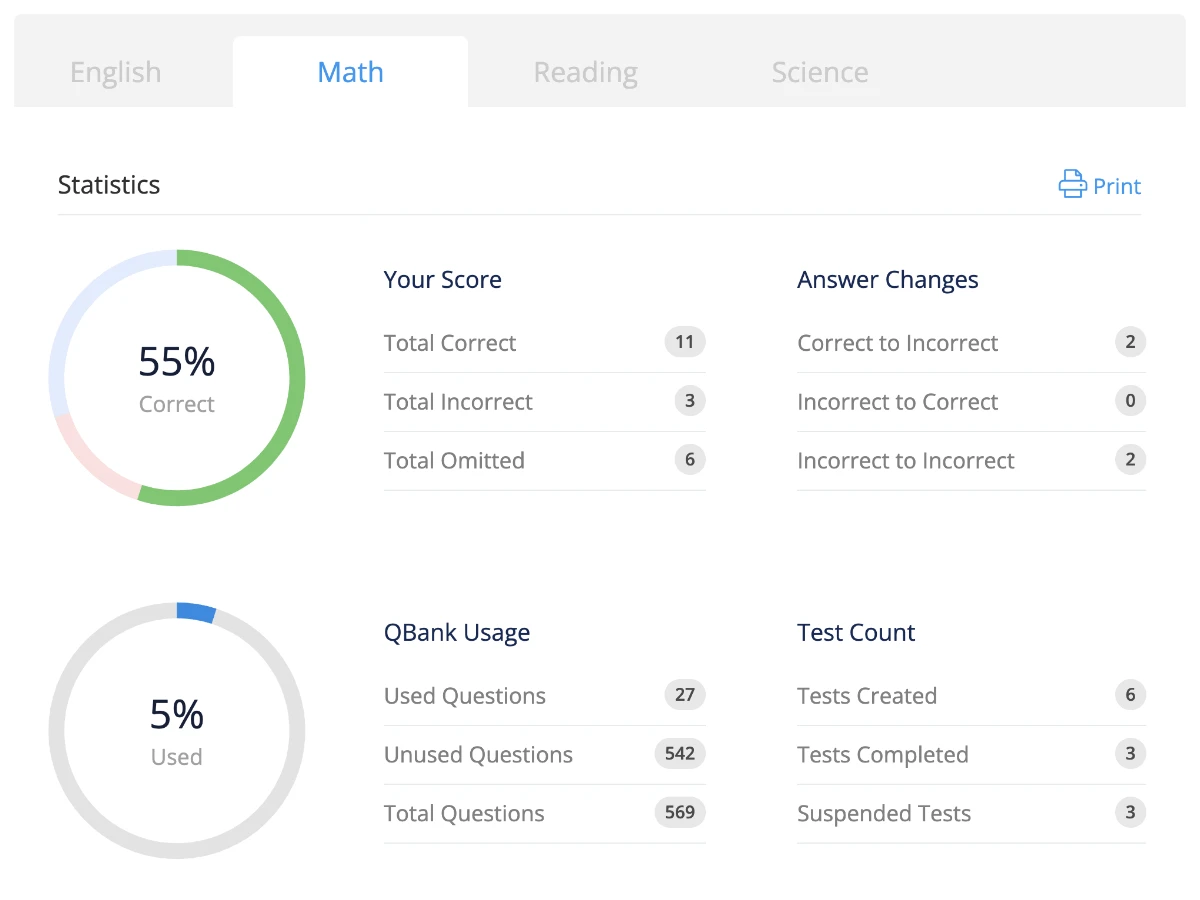
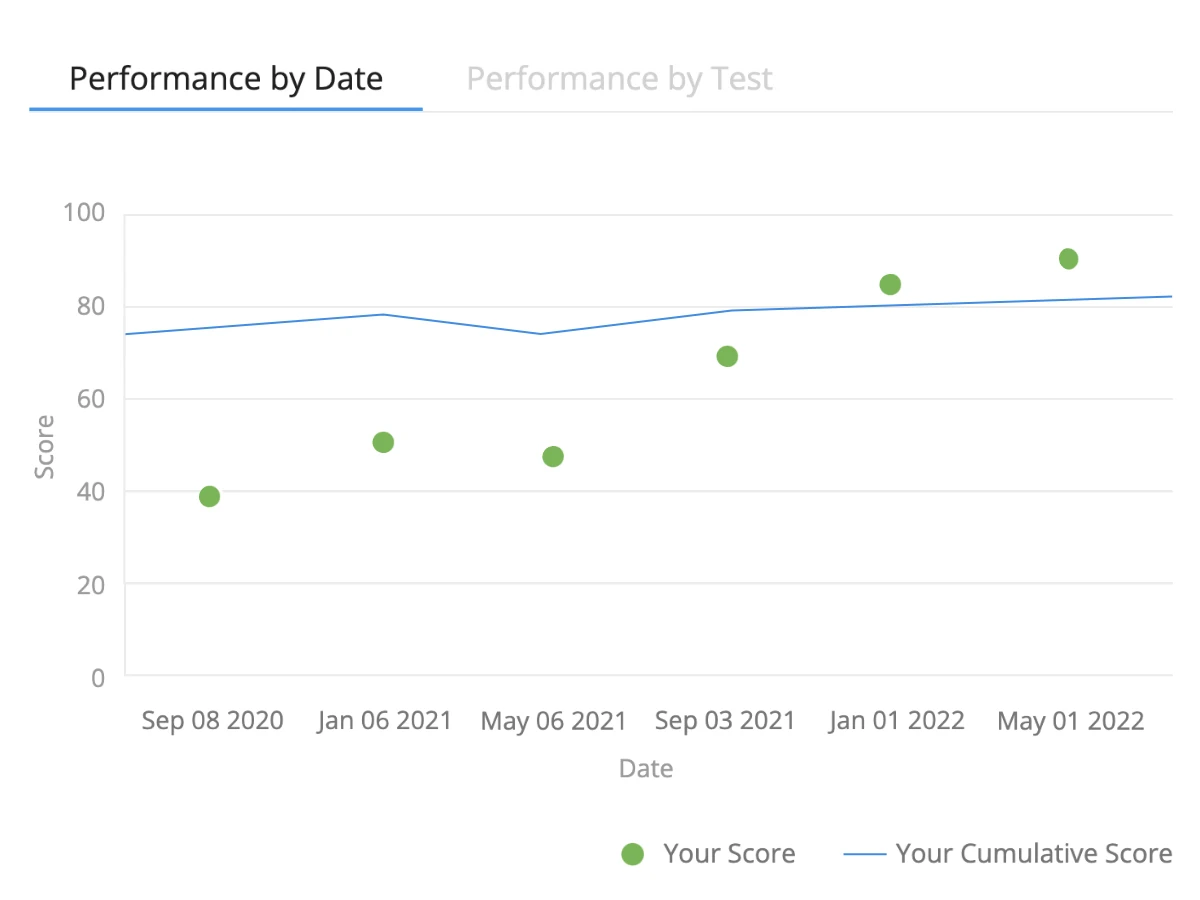
Track Your Progress With Advanced Analytics
- Utilize your time efficiently by focusing on areas of growth and development rather than revisiting what you already know.
- Our advanced analytics provide immediate feedback for each practice test and allow you to measure your progress with score predictors.
- You can even compare your results to your peers. That way, you always know exactly what you need to study.
Track Your Progress With Advanced Analytics
- Utilize your time efficiently by focusing on areas of growth and development rather than revisiting what you already know.
- Our advanced analytics provide immediate feedback for each practice test and allow you to measure your progress with score predictors.
- You can even compare your results to your peers. That way, you always know exactly what you need to study.
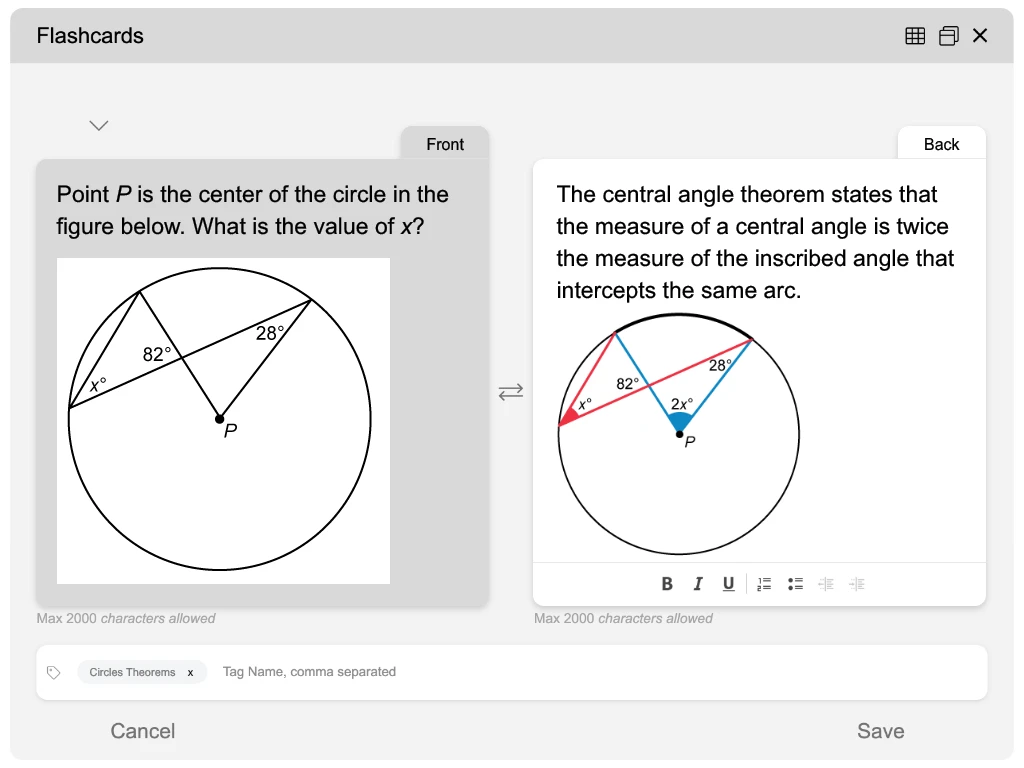
Features: My Notebook & Flashcards
- Find a helpful explanation? Like a visualization of a formula? Just click, highlight, and select create notes or flashcards.
- It’s easy to transfer QBank visual and written content to your digital My Notebook and Flashcards and keep them all organized by topic or custom tag.
- The best part? It’s always in arms reach with our mobile app.
Features: My Notebook & Flashcards
- Find a helpful explanation? Like a visualization of a formula? Just click, highlight, and select create notes or flashcards.
- It’s easy to transfer QBank visual and written content to your digital My Notebook and Flashcards and keep them all organized by topic or custom tag.
- The best part? It’s always in arms reach with our mobile app.
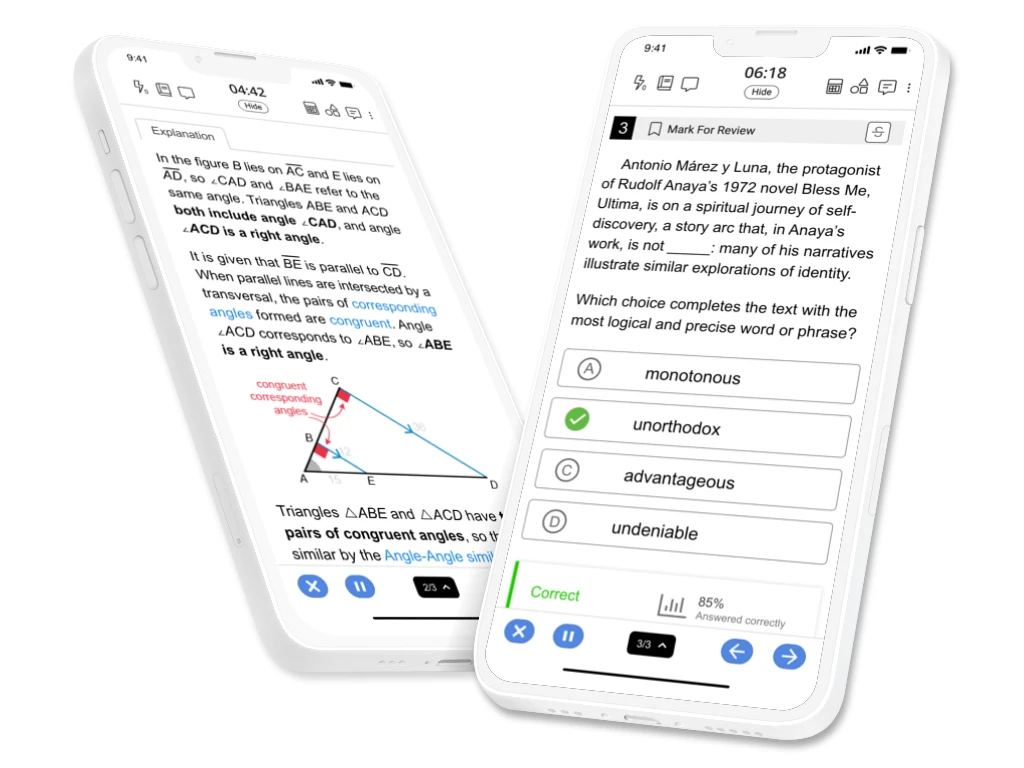
We make the real thing feel like practice
We believe that if practice feels like the actual exam, then the actual exam will feel like practice. UWorld simulates the actual ACT, so you’ll have all the confidence you need come exam day.
Practice ACT Math Sample Questions Anywhere at Any Time
Hear from Our Happy Students
I got a 35 from studying using UWorld, it has the best question bank along with the most informative explanations.”
UWorld contributed to a 10 point increase for me on the ACT. The website was FANTASTIC for me to practice on the go. I especially liked the math section.”
The primary reason for me being extremely likely to recommend UWorld to a friend is because it has helped me prepare and achieve a 35 Composite ACT Score!
Frequently Asked Questions (FAQs)
Our ACT Math practice tests cover everything you’ll need to pass the actual exam, from Pre-algebra to Trigonometry. Check out our “About the ACT Math page” for details.