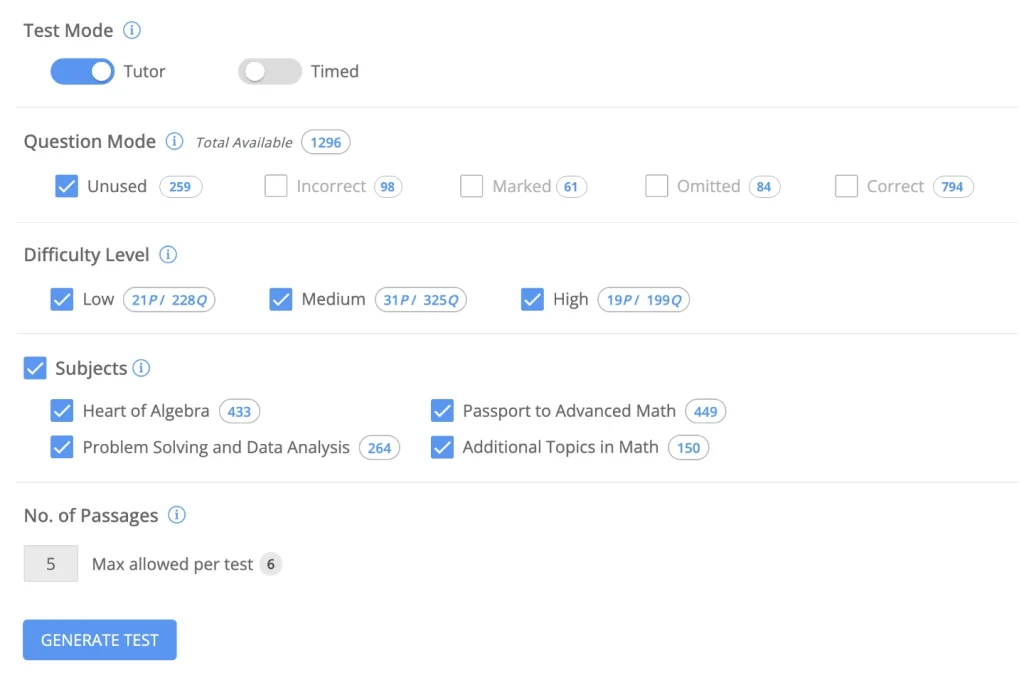
SAT® Math Practice Tests and Questions
Generate endless personalized SAT® Math practice tests containing hundreds of exam-level questions. By simulating the actual exam experience during practice, you can ensure that the real test will feel familiar and comfortable.
*Digital SAT Math Practice Bank available July 2023!
Benefits of Practicing with SAT Math Exam-Like Questions
Unlimited Exam-level Practice
Customized to Your Needs
Understand the Why
SAT Math Sample Questions
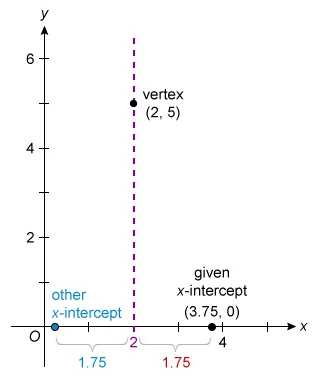
The quadratic function f is graphed in the xy-plane, where y = f(x). One of the x-intercepts of this graph is ( 15 / 4 , 0) and its vertex is (2, 5). What is the other x-intercept?
| A. (- 15 / 4 , 0) | |
| B. (- 7 / 4 , 0) | |
| C. ( 1 / 4 , 0) | |
| D. ( 23 / 4 , 0) |
Hint: The graph of a quadratic function is a parabola. A parabola has a vertical axis of symmetry that passes through its vertex.
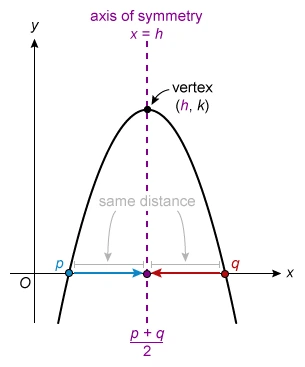
The graph of a quadratic function is a parabola. The parabola’s vertex is on a vertical axis of symmetry that is halfway between any two points on the parabola that have the same y-value.
All x-intercepts have the same y-value, so the vertex is halfway between the x-intercepts. Therefore, the x-value of the vertex is equal to the average of the x-intercepts.
Find the horizontal distance between the axis of symmetry and the given x-intercept. Then use this distance to find the x-intercept that is on the other side of the axis of symmetry.
Note: It may be simpler to consider the values in decimal form.
The given x-intercept is 1.75 units to the right of the axis of symmetry (x = 2), so the other x-intercept must be 1.75 units to the left of it. Subtract to see that the other x-intercept is 2 − 1.75 = 0.25.
Rewrite 0.25 as 1 / 4 to match the form of the choices. Therefore, the other x-intercept of the graph of f(x) is ( 1 / 4 , 0)
Note: It is also possible to set up an equation for the average of the x-intercepts and solve for the other x-intercept.
(Choice A) (- 15 / 4 , 0) may result from mistaking the axis of symmetry to be the y-axis (instead of the line x = 2).
(Choice B) (- 7 / 4 , 0) may result from calculating the horizontal distance between the given x-intercept and the vertex and then subtracting it from 0 (instead of from 2).
(Choice D) ( 23 / 4 , 0) may result from adding the x-values of the vertex and the given x-intercept. It is possible to eliminate this choice because it is on the same side of the vertex as the given x-intercept.
Things to remember:
A parabola has a vertical axis of symmetry that passes through its vertex. The axis of symmetry is halfway between any two points on the parabola that have the same y-value.
A rectangle has a length of 8 inches and a width of 11 inches. What is the perimeter, in inches, of this rectangle?
Submit Next Question
Hint : The perimeter of a polygon is equal to the sum of the side lengths.
The perimeter of a polygon is equal to the sum of the side lengths. Both pairs of opposite sides of a rectangle are congruent, so the formula for the perimeter of a rectangle with length l and width w is P = 2l + 2w .
Perimeter of a rectangle
P = 2l + 2w
It is given that the length is 8 inches and the width is 11 inches. Plug in l = 8 and w = 11 and solve for P.
The perimeter of this rectangle is 38 inches.
Things to remember:
- The perimeter of a polygon is equal to the sum of its side lengths.
- Both pairs of opposite sides of a rectangle are congruent, so the perimeter of a rectangle with length l and width w is P = 2l + 2w .
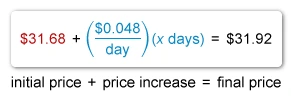
On a certain date, the average price per barrel of crude oil was $31.68. The average price increased at a constant rate every day for x days, until the price per barrel reached $31.92. The equation 31.68 + 0.048x = 31.92 represents this situation. Which of the following best describes the meaning of the number 0.048 in the equation?
- The total increase, in dollars, in the average price per barrel of crude oil after x days
- The average price per barrel of crude oil
- The percentage increase in the average price per barrel of crude oil
- The rate of change, in dollars per day, in the average price per barrel of crude oil
Hint : In the given equation, the values 31.68 and 31.92 represent dollar amounts, so 0.048x must also represent a dollar amount.
The given equation 31.68 + 0.048x = 31.92 models the average price per barrel of crude oil where the price increased from $31.68 to $31.92.
Therefore, 0.048x is the increase in the average price per barrel after x days. Each term in an equation must have the same units, so the units of 0.048x must be dollars.
It is given that the price increased at a constant rate every day, so an increase of 0.048x dollars means that the price increased 0.048 dollars per day for x days.
Therefore, 0.048 is the rate of change, in dollars per day, in the average price per barrel of crude oil.
(Choice A) This choice describes the meaning of 0.048x (instead of 0.048).
(Choice B) This choice is incorrect because the average price per barrel starts at $31.68 and increases each day for x days to $31.92.
(Choice C) This choice may result from mistaking x to be the average price per barrel (instead of a number of days).
Things to remember:
A total amount (ex. cost, time) is generally a fixed amount (ex. initial amount) plus any variable amount (ex. number of items multiplied by the rate per item).
Which of the following is an equivalent form of k2 − 14km + 49m2 ?
- (k + 7m)2
- (k – 7m)2
- (k + 2m)(k − 7m)
- (k + 7m)(k − 7m)
Hint : The first and third terms in the given expression are perfect squares.
An expression in the form a2 − 2ab + b2 factors as the perfect square (a − b)2 (proof).
In the given expression k 2 − 14km + 49m2, the term k 2 is equivalent to k ∙ k and the term 49m 2 is equivalent to 7m ∙ 7m. These terms are perfect squares k 2 and (7m)2.
The remaining term 14km is equivalent to 2 ⋅ k ⋅ 7m, so the given expression factors as a perfect square.
The given expression is equivalent to (k − 7m)2.
(Choice A) (k + 7m)2 is equivalent to k 2 + 14km + 49m2 and may result from mistakenly factoring the given expression as (a + b)2, instead of (a − b)2.
(Choice C) (k + 2m)(k − 7m) is equivalent to k 2 − 5km − 14m2 (instead of k 2 − 14km + 49m2).
(Choice D) (k + 7m)(k − 7m) is equivalent to k 2 − 49m2 and may result from mistakenly factoring the given expression as a difference of two squares a2 − b2.
Things to remember:
- An expression in the form a2 + 2ab + b2 factors as the perfect square (a + b)2.
- An expression in the form a2 − 2ab + b2 factors as the perfect square (a − b)2.
Alternate Method :
It is also possible to expand each choice and simplify to see which is equivalent to k 2 − 14km + 49m2.
Each choice is equivalent to a product of two binomials. Distribute each term in the first factor to each term in the second, and then combine like terms.
The expression that is equivalent to the given expression is (k − 7m)2.
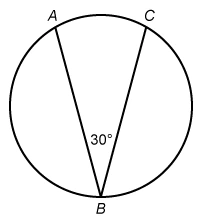
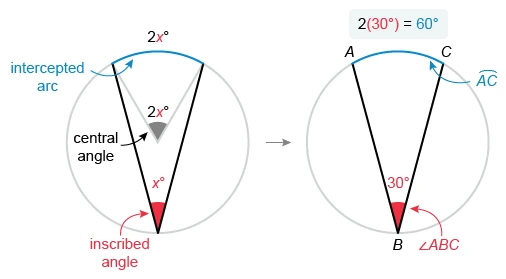
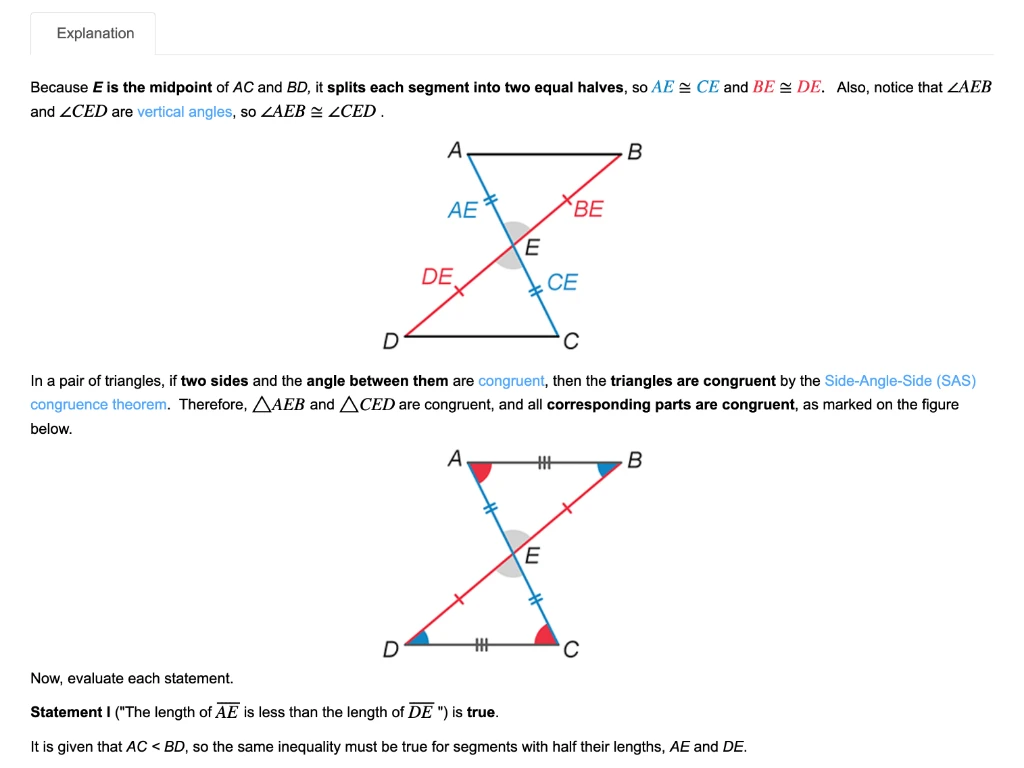
In the figure above, points A, B, and C lie on the circle. What is the measure, in degrees, of arc ?
- 15
- 30
- 60
- 330
Hint : The measure of an arc is equal to the measure of its intercepting central angle.
The measure of an arc is equal to the measure of its intercepting central angle. The central angle theorem states that the measure of a central angle is twice that of any inscribed angle that intercepts the same arc.
Therefore, the measure of an arc is twice that of its intercepting inscribed angle. No central angle is given, so use the measure of inscribed ∠ABC (30°). Multiply 30° by 2 to find the measure of intercepted arc
The measure of arc is 60°.
Note: The measure of an arc is an angle measurement. It is distinct from arc length, which is a part of the circumference of a circle.
(Choice A) 15 may result from mistaking the measure of an arc to be half (instead of twice) the measure of the intercepting inscribed angle.
(Choice B) 30 may result from mistaking the measure of an arc to be the same as (instead of twice) the measure of the intercepting inscribed angle.
(Choice D) 330 may result from a combination of the error described in Choice B and subtracting the incorrect measure from 360°.
Things to remember:
- The measure of an arc is equal to the measure of its intercepting central angle.
- The central angle theorem states that the measure of a central angle is twice the measure of any inscribed angle that intercepts the same arc.
Like our questions? Get Them Every Week—Free!
Signup to study free UWorld questions every week
Get Closer to 800 on the SAT Math Section with UWorld’s Integrated Learning System
Study content crafted by subject matter experts, assess yourself with exam-level practice, measure your performance, target your weaknesses with focused study, and repeat.
"UWorld pulled my SAT math from 650 to 800 and fundamentally retaught me the basics."
Create Unlimited Practice Tests with Exam-Level Questions
- Generate unlimited practice tests from hundreds of exam-level questions.
- Target your weaknesses by customizing a test based on topic, a custom tag, or even just questions you’ve previously gotten wrong.
Create Unlimited Practice Tests with Exam-Level Questions
- Generate unlimited practice tests from hundreds of exam-level questions.
- Target your weaknesses by customizing a test based on topic, a custom tag, or even just questions you’ve previously gotten wrong.
Understand Why an Answer is Right or Wrong
- It's not enough to know the right answer. You must understand why it's right or wrong.
- That's why we provide in-depth answer explanations complemented by professionally produced images for every answer choice.
Understand Why an Answer is Right or Wrong
- It's not enough to know the right answer. You must understand why it's right or wrong.
- That's why we provide in-depth answer explanations complemented by professionally produced images for every answer choice.
Track Your Progress With Advanced Analytics
- Optimize your study time by focusing on new and challenging material, rather than reviewing what you already know.
- Track your progress using score predictors, identify areas for which offer the most growth potential, compare your performance to that of your peers, and receive comprehensive feedback summaries for every test.
Track Your Progress With Advanced Analytics
- Optimize your study time by focusing on new and challenging material, rather than reviewing what you already know.
- Track your progress using score predictors, identify areas for which offer the most growth potential, compare your performance to that of your peers, and receive comprehensive feedback summaries for every test.
Features: My Notebook & Flashcards
- Transferring QBank visual and written content to your digital My Notebook and Flashcards is a breeze. Effortlessly create notes or flashcards by simply clicking, highlighting, and selecting information you’d like to review later.
- Customize our study aids to align with your learning style and maintain organized categorization by topic or custom tags.
- The greatest advantage? Our mobile app ensures that these invaluable learning tools are always readily available.
Features: My Notebook & Flashcards
- Transferring QBank visual and written content to your digital My Notebook and Flashcards is a breeze. Effortlessly create notes or flashcards by simply clicking, highlighting, and selecting information you’d like to review later.
- Customize our study aids to align with your learning style and maintain organized categorization by topic or custom tags.
- The greatest advantage? Our mobile app ensures that these invaluable learning tools are always readily available.
Get Exam-Ready with Exam-level Practice!
We believe that if practice feels like the actual exam, then the actual exam will feel like practice. UWorld simulates the actual SAT, so there won’t be any surprises on exam day.
Practice SAT Math Sample Questions Anywhere at Any Time
Excellent Exam Results Make Happy Students
UWorld's Qbank is extremely satisfactory to my needs as a Digital SAT test-taker! It helped me in both the mathematics section & the writing section, extremely. I also went from getting almost 47/58 in math to an all-time flawless math score, and I'm vastly grateful for this product.
Both the SAT and ACT Qbanks have helped to improve my scores immensely, and I feel that the questions are an accurate reflection of questions given on the tests. I liked that for the math questions, they were more difficult compared to the actual test.
It's amazing and it helped me improve my ACT and SAT scores. I've never felt more confident than after using uworld.
Frequently Asked Questions (FAQs)
Setting the goal of getting a high score on the SAT Math section may make you anxious. It’s too big, too general, and too difficult to measure
Let’s explore how to make this goal manageable:
- Take a self-assessment with score prediction to set a baseline and determine which topics are a challenge to you.
- Create your overarching goal. (e.g. “Improve my Math score by 100 points in 3 months.”)
- Break down your smaller goals. (e.g., “Practice a mix of 20 geometry and calculus problems per day, review for mistakes, and create a flashcard identifying the blind spot responsible for that mistake.)