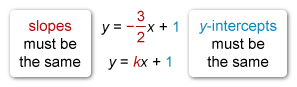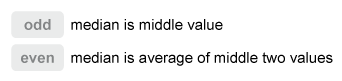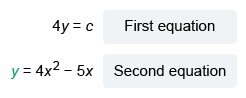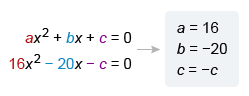Below, we've broken down the SAT® Math section into its 4 official domains: Algebra, Problem Solving and Data Analysis, Advanced Math, and Geometry and Trigonometry. Read on for each domain's examples, questions, strategies, and tricks.

Algebra
The SAT Algebra domain focuses on assessing your ability to analyze, fluently solve, and create linear equations and inequalities, as well as solve systems of equations using various techniques. Approximately 13-15 questions on the SAT Math section are derived from this domain.
Strategies to Ace Algebra Questions
The key to solving linear functions effectively is understanding what they represent. Start by drawing or annotating graphs, as they help visualize slopes, intercepts, and the intersection point of two lines — often the solution to a system of equations. If a graph isn't provided, try rewriting the equation in slope-intercept form to make plotting easier.
When faced with multi-step problems, slow down and work through each step carefully to avoid small mistakes. Practicing complex problems regularly can help you build confidence and reduce test-day anxiety. Be sure to show your work and proceed methodically.
It's also important to memorize essential formulas related to linear equations, absolute values, and graphing — this forms the core of your algebra toolbox. Lastly, try plugging the answer choices back into the equation for multiple-choice questions. This strategy can be especially useful for verifying solutions to tricky problems involving equations or inequalities.
Algebra examples
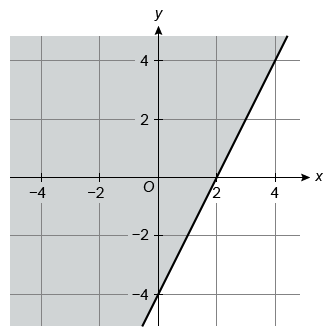
The solutions to which inequality are represented by the shaded region of the graph?
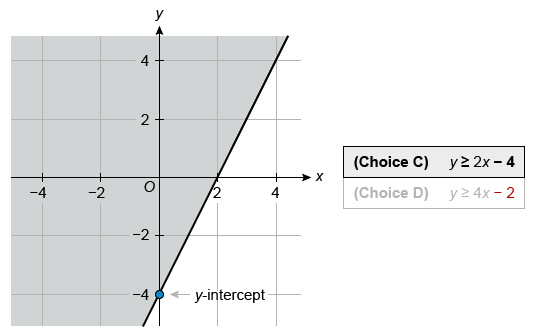
| A. y ≤ −2x − 4 | |
| B. y ≤ −4x − 2 | |
| C. y ≥ 2x − 4 | |
| D. y ≥ 4x − 2 |
Hint:
The graph of a linear inequality of the form y ≥ mx + b has shading above a boundary line.
The graph of a linear inequality of the form y ≤ mx + b has shading below a boundary line.
The solutions represented by the given graph consist of all points in the shaded area and on the boundary line. Analyze the shading and the boundary line of the given graph and use a process of elimination.
The given graph is shaded above the line, so the inequality must be in the form y ≥ mx + b. Eliminate Choices A and B because they represent graphs with shading below the boundary line.
The boundary line of the given graph has a y-intercept of −4, so the boundary line equation in slope-intercept form must be y = mx − 4. Therefore, the inequality must be in the form y ≥ mx − 4.
Eliminate Choice D because it does not match this form.
Of the choices, only the inequality in Choice C has a graph with shading above the boundary line and a y-intercept of −4. By process of elimination, Choice C has the solutions represented by the shaded region.
Elimination strategy: The boundary line of the given graph has a positive slope. Therefore, it is possible to eliminate Choices A and B because each has a boundary line equation with a negative slope.
Things to remember:
- The graph of a linear inequality of the form y > mx + b or y ≥ mx + b has shading above a boundary line.
- The graph of a linear inequality of the form y < mx + b or y ≤ mx + b has shading below a boundary line.
- The equation of the boundary line in slope intercept form is y = mx + b, where m is the slope and b is the y-intercept.
In the xy-plane, line p is parallel to the line represented by the equation y = −2x + 7. If line p passes through the points (0, 0) and (9, r), what is the value of r ?
Hint:
First determine the slope of a line parallel to line l
. Then use this slope and the given point to determine the y-intercept of line k.
Parallel lines have the same slope but different y-intercepts. It is given that line p is parallel to the line represented by the equation y = −2x + 7, so they have the same slope.
The given equation is in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept. Compare y = −2x + 7 to the slope-intercept form y = mx + b to determine the slope m.
The slope of the given equation is −2, so the slope of line p is also −2. It is given that line p passes through the point (0, 0), so the y-value of the y-intercept of line p is 0.
Plug m = −2 and b = 0 into y = mx + b to find the equation of line p.
y = mx + b Slope-intercept form
y = −2x + 0 Plug in m = −2 and b = 0
The equation of line p is y = −2x. The question asks for the value of r, and it is given that line p passes through the point (9, r).
Plug the given point (x, y) = (9, r) into the equation of line p and solve for r.
y = −2x Slope-intercept form
r = −2(9) Plug in x = 9 and y = r
r = −18 Multiply
The value of r is −18.
Note: It is also possible to use the given points to find the slope of line p in terms of r, then find the value of r.
Things to remember:
- The slope-intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept of the line.
- Parallel lines have the same slope but different y-intercepts.
- To find the slope of a line given two points (x1, y1) and (x2, y2), use the slope formula y2-y1 / x2-x1
y = - 3 / 2 x + 1
y = kx + 1
In the system of equations shown, k is a constant. If the system has infinitely many solutions, what is the value of k ?
Hint:
Each linear equation in the given system is in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept.
The given system consists of linear equations in slope-intercept form y = mx + b, where m is the slope and b is the y-intercept. Therefore, it is efficient to consider these features of its graph to find the value of k.
It is given that the system has infinitely many solutions, so its graph must be a single line (the lines intersect at every point). Equations that represent the same line have the same slope and the same y-intercept.
Compare the two equations to see that the y-intercepts are the same (1 = 1). Identify the value of k that makes the slopes the same.
The value of k is - 3/ 2 .
Things to remember:
- A system has infinitely many solutions if its graph is a single line because the lines intersect at every point.
- Equations that represent the same line have the same slope and the same y-intercept.
Problem-Solving and Data Analysis
This category focuses on problems involving ratios, percentages, and 1- or 2-variable data. These questions often reference statistical terms (mean, median, mode), scatter plots, lines of best fit, data collection methods, and percent or ratio relationships. Box-and-whisker plot questions, when included, also fall under this domain. It typically accounts for 5-7 questions on the SAT Math section.
Strategies to Ace Problem-Solving and Data Analysis Questions
As you prepare for this section, ensure you understand the key technical terms' definitions and know how to calculate values or interpret data sets. SAT Math questions in this domain often include incorrect answer choices based on common mistakes or misconceptions. For instance, if a question asks for the mean of a dataset, one of the answer choices may be the median. Mastering the relevant vocabulary will help you approach these questions with greater confidence and fewer distractions.
Another common challenge is that data points may be presented out of order. This can be especially important when calculating values like the median, where numerical order matters. Taking a few seconds to reorder the values can help you avoid simple but costly errors.
Problem-Solving and Data Analysis examples
The population of a certain town decreased by 4% from 2005 to 2015. If the population in 2015 is k times the population in 2005, what is the value of k ?
To decrease a value by p%, multiply it by ( 1 - p / 100 )
The question states that the population in 2015 is k times the population in 2005.
It is also given that the population decreased by 4% from 2005 to 2015. To decrease a value by p%, multiply it by (1 - p / 100 ) . Therefore, the 2015 population is equal to (1 - 4 / 100 ) multiplied by the 2005 population.
Therefore, k must equal 1 - 4 / 100 . Simplify 1 - 4 / 100 to write the value of k as a decimal.
1 -
4
/
100
Value of k
1 - 0.04 Divide
0.96 Subtract
The value of k is 0.96.
Note: It is also possible to rewrite 1 - 4 / 100 as a fraction and simplify the result.
Things to remember:
- To increase a value by p%, multiply it by (1 + p / 100 )
- To decrease a value by p%, multiply it by (1 - p / 100 ).
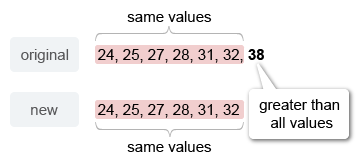
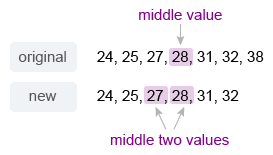
24, 25, 27, 28, 31, 32, 38
The data set shown represents the overall diameters, in inches, of 7 different sizes of tires sold by an auto shop. The tire size with a diameter of 38 inches was recorded incorrectly. If the diameter of 38 inches is removed from the data set, which statement best describes the effect on the mean and median diameters of the 7 tire sizes?
| A. Both the mean and the median will increase. | |
| B. Both the mean and the median will decrease. | |
| C. The mean will increase, and the median will decrease. | |
| D. The mean will decrease, and the median will increase. |
Hint:
Notice that the removed value of 38 is greater than all the values in the original data set.
The median of a data set with an odd number of values is the middle value, and the median of a data set with an even number of values is the average of the middle two values.
The question asks about the mean and median tire diameters if the diameter of 38 inches is removed from the data set. Compare the means and medians of the original data set and the new data set separately.
Mean
If a value is added to or removed from a data set, the mean changes unless the value added or removed is equal to the mean.
It is given that the value 38 is removed from the data set. Notice that 38 is greater than all the other values in the original data set.
Therefore, 38 must be greater than the mean of the original data set. When a value greater than the mean is removed from a data set, the mean of the data set decreases.
Note: Although not necessary to answer the question, it is possible to calculate and compare the mean of each data set.
Median
The median of a data set with an odd number of values is the middle value, and the median of a data set with an even number of values is the average of the middle two values.
Notice that the values are ordered from least to greatest. The original data set has 7 values (odd) and the new data set has 6 values (even).
The middle value of the original data is 28, so the median of the original data is 28.
The middle two values of the new data are 27 and 28, so the median of the new data is their average
27+28
/
2
= 27.5.
The median decreases as a result of the removed value.
Therefore, the statement that best describes the effect on the mean and median tire diameters is: "Both the mean and the median will decrease."
Things to remember:
-
If a value is removed from a data set and the value is:
-
less than the mean, the mean will increase.
-
greater than the mean, the mean will decrease.
-
-
The median of a data set with an odd number of values is the middle value, and the median of a data set with an even number of values is the average of the middle two values.
A set designer is painting a backdrop for a play at a rate of 18 square inches per minute. At what rate, in square feet per hour, is the set designer painting? (1 foot = 12 inches)
Hint:
First use the given unit conversion 1 foot = 12 inches to find a conversion for square inches and square feet.
To convert from square inches per minute to square feet per hour, convert both the area units (square inches to square feet) and the time units (minutes to hours).
First convert square inches to square feet, and then convert minutes to hours.
To convert units, multiply by a conversion factor that cancels the old unit and replaces it with the new unit. A conversion factor is a fraction that is equivalent to 1, so it changes only the units and not the quantity.
square inches → square feet
The old unit is square inches, and the new unit is square feet. The given conversion is 1 foot = 12 inches, so it is necessary to first find a conversion for square inches and square feet.
The desired units are square units, so square both sides of the given conversion to determine the relationship between square inches and square feet.
| 1 foot = 12 inches | Given conversion |
| (1 foot)2 = (12 inches)2 | Square both sides |
| (1 foot)(1 foot) = (12 inches)(12inches) | Apply exponent on both sides |
| 1 square foot = 144 square inches | Multiply |
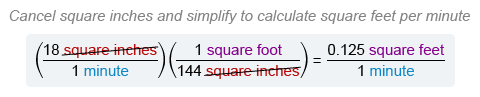
Now use the conversion 1 square foot = 144 square inches to convert square inches to square feet. Multiply 18 square inches per minute by the conversion factor 1 square foot / 144 square inches ) .
Therefore, the set designer is painting at a rate of 0.125 square feet per minute.
minutes → hours
To convert from minutes to hours, multiply by a conversion factor with minutes in the numerator and an equivalent number of hours in the denominator.
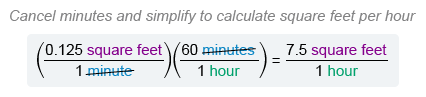
There are 60 minutes in 1 hour, so the conversion factor is 60 minutes / 1 hour ).
Therefore, the set designer is painting at a rate of 7.5 square feet per hour.
Tactic: It is possible to convert from square inches per minute to square feet per hour in a single calculation.
Things to remember:
-
To convert from one unit to another, multiply by a conversion factor that cancels the old unit and replaces it with the new unit.
-
To convert between square units (ex. square feet and square inches), square both sides of the conversion between their linear units (feet and inches).
Advanced Math
This domain covers a broad range of topics that go beyond basic algebra and extend into Algebra II, with some overlap into precalculus depending on your coursework. It includes nonlinear functions, expressions, and equations such as quadratics, exponential and square root functions, and systems of equations with 2 or more variables. You can recognize these questions by references to quadratics in various forms, expressions with exponents or roots, and function notation, especially composite functions (e.g., g(f(x))). This domain typically accounts for 13-15 questions on the SAT Math section.
Strategies to Ace Advanced Math Questions
This category primarily focuses on higher-order functions and expressions, so familiarize yourself with manipulating the different expressions you will encounter. For instance, solving or rewriting quadratic functions using techniques such as factoring and completing the square, and the quadratic formula will significantly enhance your comfort and consistency with these questions. Similarly, it's beneficial to understand how to rewrite exponents and roots in terms of each other, as this can simplify and make many equivalent expression questions easier.
Advanced Math examples
In the xy-plane, a line with equation 4y = c for some constant c intersects the parabola y = 4x2 − 5x at exactly one point. What is the value of c?
Hint:
Intersection points (x, y) on the graph of a system of equations correspond to solutions to the system.
Intersection points (x, y) on the graph of a system of equations correspond to solutions to the system. It is given that the system has exactly one intersection point, so the system must have exactly one solution.
Notice that y is isolated in the second equation. Use substitution to get an equation in terms of only x and then use the discriminant to solve for c.
Substitute 4x2 − 5x for y in the first equation.
| 4y = c | First equation |
| 4(4x2 − 5x) = c | Substitute |
Now rewrite the resulting quadratic equation in standard form ax2 + bx + c = 0. First distribute 4 and then collect all terms on one side of the equation.
| 4(4x2 − 5x) = c | |
| 4(4x2) − 4(5x) = c | Distribute 4 to 4x2 and 5x |
| 16x2 − 20x = c | Multiply |
| 16x2 − 20x − c = 0 | Subtract c from both sides |
A quadratic equation in standard form ax2 + bx + c = 0 has exactly one solution when the discriminant b2 − 4ac is equal to 0. Compare the resulting equation to standard form to identify the values of a, b, and c.
Note: The constant term c in the equation 16x2 − 20x − c = 0 is NOT the same as the c in standard form.
Plug these values into the discriminant b2 − 4ac and simplify.
| b2 − 4ac | Discriminant |
| (−20)2 − 4(16)(−c) | Plug in a = 16, b = −20, and c = −c |
| 400 − 4(16)(−c) | Apply the exponent |
| 400 + 64c | Multiply |
The discriminant is 400 + 64c, so the system has exactly one solution when 400 + 64c is equal to 0. Set it equal to 0 and solve for c.
| 400 + 64c = 0 | Set discriminant equal to 0 |
| 400 = −64c | Subtract 64c from both sides |
| −6.25 = c | Divide by −64 on both sides |
Therefore, the value of c is −6.25.
Note: It is also possible to simplify - 400 / 64 as a fraction to see that the value of c is - 25 / 4 .
Things to remember:
-
To find the number of solutions to a linear and quadratic system, first use the substitution method to create a single equation in terms of only x.
-
A quadratic equation in standard form has exactly one solution when the discriminant b2 − 4ac is equal to 0.
Alternate Method :
In the given system of equations, the graph of 4y = c is a horizontal line and the graph of y = 4x2 − 5x is a parabola. It is given that this system has a single intersection point.
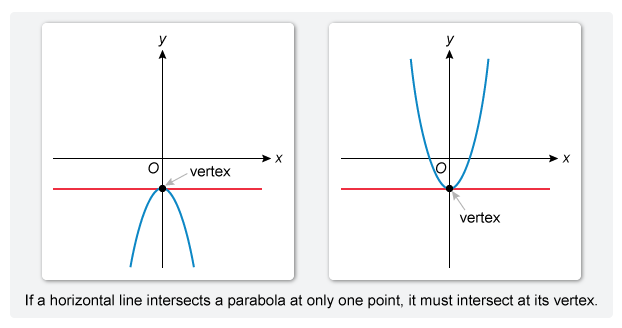
A horizontal line and a parabola with a single intersection point must intersect at the vertex of the parabola.
Therefore, the coordinates of the vertex must satisfy both equations in the system. The desired value c appears in the first equation 4y = c.
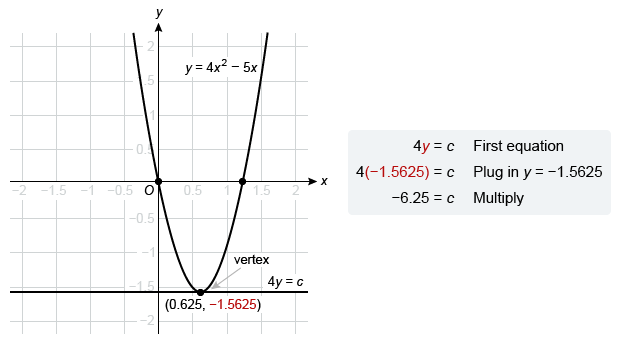
Use a calculator to identify the vertex of y = 4x2 − 5x, and plug its y-coordinate into 4y = c to solve for c. The vertex is (0.625, −1.5625), so y = −1.5625.
Therefore, the value of c is −6.25.
Note: It is also possible to use the vertex formula to calculate the x-value of the vertex (0.625) and then plug x = 0.625 into y = 4x2 − 5x to get the y-value of the vertex (−1.5625).
Things to remember:
-
A linear equation in the form y = c, where c is a constant, represents a horizontal line.
-
A solution to a system of equations is a point where the graphs of the equations intersect in the xy-plane.
-
If a horizontal line intersects a parabola at only one point, it must intersect at the vertex of the parabola.
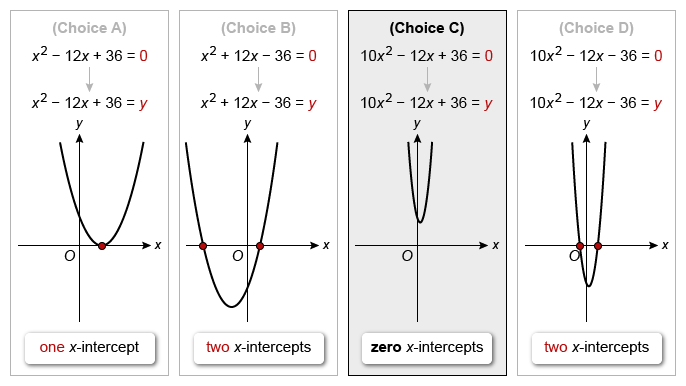
Which of the following quadratic equations has no real solutions?
| A. x2 − 12x + 36 = 0 | |
| B. x2 + 12x − 36 = 0 | |
| C. 10x2 − 12x + 36 = 0 | |
| D. 10x2 − 12x − 36 = 0 |
Hint:
A quadratic equation in one variable has 0, 1, or 2 solutions.
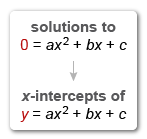
The real solutions to a quadratic equation in the form ax2 + bx + c = 0 correspond to the x-intercepts on the graph of y = ax2 + bx + c because x-intercepts have a y-value of 0.
To determine which equation has no real solutions, graph the corresponding equation for each choice to see which has no x-intercepts.
The only graph that has no x-intercepts is the graph of y = 10x2 − 12x + 36. Therefore, the equation 10x2 − 12x + 36 = 0 has no real solutions.
Things to remember:
The solutions to a quadratic equation in the form 0 = ax2 + bx + c correspond to the x-intercepts on the graph of y = ax2 + bx + c.
Alternate Method :
A quadratic equation in standard form ax2 + bx + c = 0 has no real solutions when the discriminant b2 − 4ac is less than 0. The discriminant is the expression under the square root in the quadratic formula.
Compare the equation in each choice to standard form ax2 + bx + c = 0 to identify the values of a, b, and c. Then plug the values of a, b, and c into b2 − 4ac and simplify to see which results in a negative value.
Note: The term x2 is the same as 1x2.
The equation in Choice C has a negative discriminant, so the equation that has no real solutions is 10x2− 12x + 36 = 0.
Elimination strategy: It is possible to use the inequality b2 − 4ac < 0 and analyze the values of a, b, and c in each equation to eliminate Choices B and D.
Things to remember:
The number of solutions to a quadratic equation ax2 + bx + c = 0 can be determined by the discriminant b2 − 4ac, the quantity under the square root in the quadratic formula.
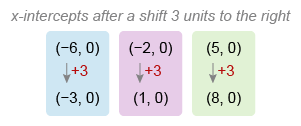
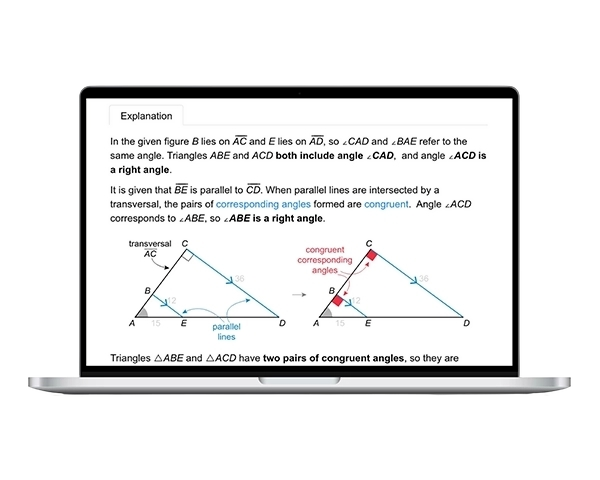
The function f is defined by f(x) = (x + 6)(x + 2)(x − 5), and the function g is defined by g(x) = f(x − 3). The graph of y = g(x) in the xy-plane has x-intercepts at (a, 0), (b, 0), and (c, 0), where a, b, and c are distinct constants. What is the value of abc ?
Hint:
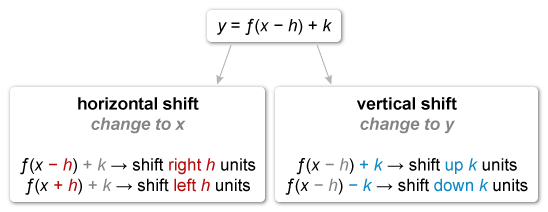
The function g(x) = f(x − 3) is defined in terms of f(x), so g represents a horizontal shift to the function f.
The function g(x) = f(x − 3) is defined in terms of f(x), so g represents a transformation to the function f.
For any function f(x), the graph of y = f(x − h) + k is the graph of y = f(x) transformed by a horizontal shift of h units and a vertical shift of k units.
In g(x) = f(x − 3), the number 3 is subtracted from the input x so it represents a horizontal shift of 3 units to the right.
The question asks for the value of abc, where (a, 0), (b, 0), and (c, 0) are the x-intercepts of g(x). Find the x-intercepts of the given function f(x), and then consider the transformation to find the x-intercepts of g(x).
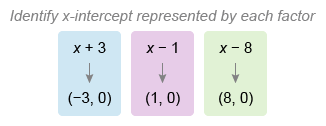
A polynomial function in factored form f(x) = (x − p)(x − q)(x − r) has x-intercepts at (p, 0), (q, 0), and (r, 0) (proof). Therefore, f(x) = (x + 6)(x + 2)(x − 5) has x-intercepts at (−6, 0), (−2, 0), and (5, 0).
Note: It is also possible to use a graphing calculator to identify the x-intercepts of f(x).
A transformation 3 units to the right means that each x-intercept of g(x) is 3 units to the right of each x-intercept of f(x). Add 3 to each x-coordinate to get the x-intercepts of g(x).
The function g(x) has x-intercepts at (−3, 0), (1, 0), and (8, 0), so let a = −3, b = 1, and c = 8. Therefore, the value of abc is −24.
Things to remember:
-
For any function f(x), the graph of y = f(x − h) + k is the graph of y = f(x) transformed by a horizontal shift of h units and a vertical shift of k units.
-
An x-intercept is a point where a graph intersects the x-axis, and its coordinates are (x, 0).
-
A polynomial function in factored form f(x) = (x − p)(x − q)(x − r) has x-intercepts at (p, 0), (q, 0), and (r, 0).
Alternate Method
The function g(x) = f(x − 3) is defined in terms of f(x). The function notation f(x − 3) represents the output (or value) of f(x) when the input is x − 3.
To get an equation for g(x) in terms of only x, substitute x − 3 for each instance of x in f(x) = (x + 6)(x + 2)(x − 5).
| f(x) = (x + 6)(x + 2)(x − 5) | Given function f(x) |
| f(x − 3) = (x − 3 + 6)(x − 3 + 2)(x − 3 − 5) | Substitute x − 3 for each instance of x |
| f(x − 3) = (x + 3)(x − 1)(x − 8) | Combine constant terms in parentheses |
Therefore, g(x) = (x + 3)(x − 1)(x − 8). The question asks for the value of abc, where (a, 0), (b, 0), and (c, 0) are the x-intercepts of g(x).
A polynomial function in factored form f(x) = (x − p)(x − q)(x − r) has x-intercepts at (p, 0), (q, 0), and (r, 0) (proof). The function g(x) is in factored form, so identify the x-intercept represented by each factor.
Note: It is also possible to use a graphing calculator to identify the x-intercepts of g(x).
The function g(x) has x-intercepts at (−3, 0), (1, 0), and (8, 0), so let a = −3, b = 1, and c = 8. Therefore, the value of abc is −24.
Things to remember:
-
The function notation f(x + a) means the output of the function f where the input is x + a. To get an equation for f(x + a), substitute the expression x + a for each instance of x in the function f(x).
-
An x-intercept is a point where a graph intersects the x-axis and its coordinates are (x, 0).
-
A polynomial function in factored form f(x) = (x − p)(x − q)(x − r) has x-intercepts at (p, 0), (q, 0), and (r, 0).
Geometry and Trigonometry
The Geometry and Trigonometry domain of the SAT Math section assesses your ability to solve problems involving area and volume formulas, lines, angles, triangles, right triangles, trigonometry, and circles. This domain typically accounts for 5-7 questions on the SAT Math section.
Strategies to Ace Geometry and Trigonometry
Since geometry and trigonometry are the focus of this domain, a solid understanding of geometric rules, theorems, and basic trigonometric concepts is essential. Be sure you can identify how angles relate to each other within parallel lines and triangles, especially which angles are congruent (equal) or supplementary (adding up to 180 degrees). Circle theorems make up a smaller portion of this section and may not appear on every exam. However, it's still important to understand how to determine the angles and dimensions of a circle. Once you're confident with the other topics, spend time reviewing these concepts to ensure you're fully prepared.
Geometry and Trigonometry in Math examples
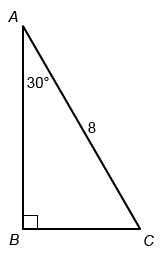
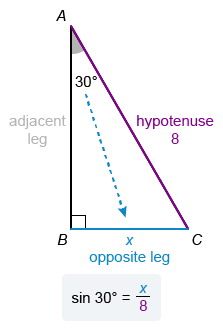
What is the length of side BC in right triangle ABC above?
| A. 2 | |
| B. 2√3 | |
| C. 4 | |
| D. 4√3 |
Hint:
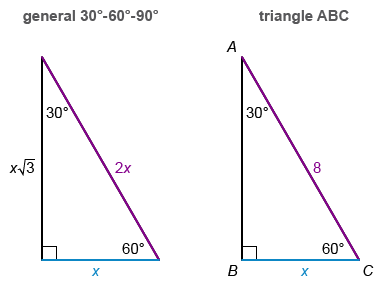
Triangle ABC is a 30°-60°-90° triangle.
Notice angle B is a right angle, so its measure is 90°. The interior angles of a triangle sum to 180° and the given measure of angle A is 30°, so the measure of angle C is 60°. Therefore, triangle ABC is a 30°-60°-90° triangle.
Side BC is across from the 30° angle, so it is the shorter leg, and BC corresponds to x. The given side AC is across from the right angle, so side is the hypotenuse and AC corresponds to 2x.
The given length of AC is 8, so set 2x = 8. Then solve for x, the length of BC.
| 2x = 8 | |
| x = 4 | Divide by 2 on both sides |
Therefore, the length of BC is 4.
(Choice A) 2 may result from mistaking the length of the hypotenuse in a 30°-60°-90° triangle to correspond to 4x (instead of 2x), where x is the length of the shorter leg.
(Choice B) 2√3 may result from a combination of the errors described in Choices A and D.
(Choice D) 4√3 is the length of side AB, but the question asks for the length of side BC.
Things to remember:
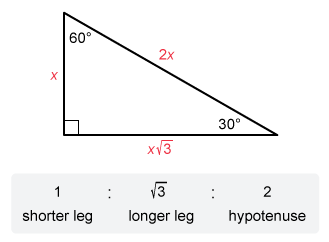
A 30°-60°-90° triangle has the following ratio of side lengths:
Alternate Method
It is also possible to use a trigonometric ratio to find a missing side length of a right triangle given an acute angle and one side.
The given measure of ∠A is 30°, and the known side AC is the hypotenuse. Side BC is across from ∠A, so it is the opposite leg. The sine ratio relates the opposite leg and the hypotenuse.
Let the desired length of BC be x. Use the sine ratio to write an equation for the sine of ∠A in terms of x.
Now solve for x, the length of BC.
| sin30° = x / 8 | Sine ratio of angle A |
| 8 sin 30° = x | Multiply by 8 on both sides |
| 4 = x | Simplify |
Note: The interior angles of a triangle sum to 180°, so the measure of angle C is 60°. Side BC is adjacent to angle C, so it is also possible to use the cosine ratio to solve for the length of BC.
Things to remember:
The sine, cosine, and tangent of an acute angle in a right triangle are equal to the following ratios of side lengths:
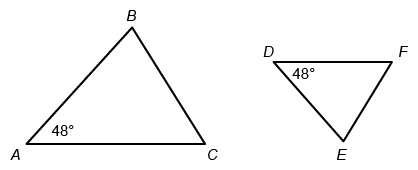
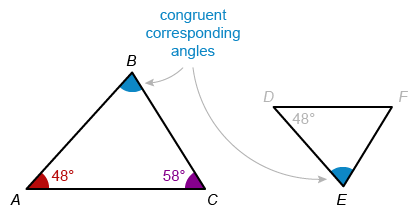
Triangles ABC and DEF are similar, where A corresponds to D, B corresponds to E, and C corresponds to F. If the measure of angle C is 58°, what is the measure, in degrees, of angle E?
Hint:
Corresponding angles of similar triangles are congruent.
It is given that right triangles ABC and DEF are similar and that B corresponds to E. Corresponding angles of similar triangles are congruent, so the desired angle E is congruent to angle B.
It is given in the figure that the measure of ∠A is 48°, and the given measure of ∠C is 58°. To find the measure of angle E, first use the given information to find the measure of ∠B.
The measures of the interior angles of a triangle sum to 180°. Set the sum of the angle measures of triangle ABC equal to 180°. Plug in the given measures of ∠A and ∠C and solve for the measure of ∠B.
| m∠A + m∠B + m∠C = 180 | Angle measures of triangle sum to 180° |
| 48 + m∠B + 58 = 180 | Plug in m∠A = 48 and m∠C = 58 |
| m∠B + 106 = 180 | Add on the left |
| m∠B = 74 | Subtract 106 from both sides |
The measure of angle B is 74°, so the measure of corresponding angle E is also 74°.
Note: Angle F is congruent to corresponding angle C, so the measure of angle F is 58°. Therefore, it is possible to set the interior angle measures of △DEF equal to 180° and solve for the measure of ∠E.
Things to remember:
- Corresponding angles of similar triangles are congruent.
- The measures of the interior angles of a triangle sum to 180°.
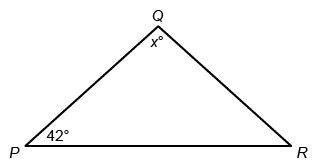
In the given triangle, PQ = QR. What is the value of x ?
Hint:
An isosceles triangle has two sides that are congruent (equal in length) and a third side called the base.
It is given that PQ = QR, so the sides PQ and QR are congruent. Therefore, triangle PQR is isosceles. It is also given that the measure of ∠QPR is 42°.
Angles QPR and QRP are opposite the congruent sides QR and QP , so ∠QPR and ∠QRP are base angles. Base angles of an isosceles triangle are congruent, so the measure of ∠QRP is also 42°.
The measures of the interior angles of a triangle sum to 180°. Set the sum of the measures of the interior angles of triangle PQR equal to 180 and solve for x.
| 42 + 42 + x = 180 | Interior angles of a triangle sum to 180 |
| 84 + x = 180 | Add |
| x = 96 | Subtract 84 from both sides |
The value of x is 96.
Things to remember:
-
An isosceles triangle has two sides that are congruent (equal in length) and a third side called the base.
-
Base angles of an isosceles triangle are congruent.
-
The measures of the interior angles of a triangle sum to 180°.
How To Fill Student-Produced Responses (SPRs) on SAT Math
While most SAT Math questions are multiple-choice, some require generating and entering your own answer. These are called student-produced responses (SPRs). Instead of selecting from given options, you'll type your answer directly into the test platform. SPRs assess your ability to solve problems independently, without the structure or cues that come with multiple-choice questions. Some of these questions may have more than one correct answer, but you are required to submit only one.
To understand all the math topics tested on the SAT, take a look at our full SAT study guide. It breaks down each concept clearly and is a great place to start your prep.

Frequently Asked Questions (FAQs)
Algebra and Advanced Math each account for approximately 13–15 questions. As a result, the most common SAT Math question types include linear functions, inequalities, nonlinear equations, and nonlinear functions.
Most SAT Math mistakes are caused by stress, unfamiliarity with problem types, or poor time management. The best way to avoid these errors is by practicing with realistic questions at varying difficulty levels. For targeted practice by topic, try our SAT question bank.
Keep in mind that every question carries equal weight. First, focus on solving the questions you’re most confident in. Once you’ve worked through the easier questions, return to the tougher ones with a clearer mindset.
Many math questions can be solved efficiently using specific strategies and formulas. Review solution explanations — like those in our SAT Course — for examples of when and how to apply them, also, practice using the built-in digital calculator to become familiar with its functions.
References
- College Board. (2024). Algebra. SAT Suite of Assessments. Retrieved April 14, 2025, from https://satsuite.collegeboard.org/sat/whats-on-the-test/math/types/algebra
- College Board. (2024). Problem-Solving and Data Analysis. SAT Suite of Assessments. Retrieved April 14, 2025, from https://satsuite.collegeboard.org/sat/whats-on-the-test/math/types/problem-solving-data-analysis
- College Board. (2024). Advanced Math. SAT Suite of Assessments. Retrieved April 14, 2025, from https://satsuite.collegeboard.org/sat/whats-on-the-test/math/types/advanced-math
- College Board. (2024). Geometry and Trigonometry. SAT Suite of Assessments. Retrieved April 14, 2025, from https://satsuite.collegeboard.org/sat/whats-on-the-test/math/types/geometry-trigonometry
- College Board. (2024). Math on the SAT. SAT Suite of Assessments. Retrieved April 14, 2025, from https://satsuite.collegeboard.org/sat/whats-on-the-test/math
Read More About Digital SAT Math
Boost your SAT Math score with our expert prep guide. Get a study plan and tips, and practice mastering algebra, geometry, and more. Start building your skills today.
SAT Math Formulas and EquationsExplore our complete Math Formula and Equation Sheet to easily review, understand, and memorize essential formulas as you prepare for your upcoming SAT math exam.
About the SAT Math SectionAcquire the confidence you need to master the SAT Math. Discover crucial test information such as format, topics, score ranges, percentiles, and more in this guide!
SAT Math Practice Tests & QuestionsGet access to a wide range of expert-made SAT Math practice tests and questions to boost your prep. Start practicing today to improve your performance on test day.