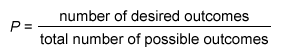The AP Statistics MCQ section consists of 40 questions, each with 5 possible answer choices. This portion of the exam must be completed in 1 hour and 30 minutes. Since it makes up 50% of the total exam weight, scoring well in this section can give you an edge over other students. Below is an overview of the proportion of questions from each unit that you will find on the exam:
| Units | Exam Weight |
|---|---|
| Unit 1: Exploring One-Variable Data | 15%-23% |
| Unit 2: Exploring Two-Variable Data | 5%-7% |
| Unit 3: Collecting Data | 12%-15% |
| Unit 4: Probability, Random Variables & Probability Distributions | 10%-20% |
| Unit 5: Sampling Distributions | 7%-12% |
| Unit 6: Inference for Categorical Data: Proportions | 12%-15% |
| Unit 7: Inference for Quantitative Data: Means | 10%-18% |
| Unit 8: Inference for Categorical Data: Chi-Square | 2%-5% |
| Unit 9: Inference for Quantitative Data: Slopes | 2%-5% |
How to Approach AP Statistics Multiple-Choice Questions?
Practice is the best way to prepare for the MCQ section of the AP Statistics exam. Beyond learning the material in class, going through high-quality, realistic practice questions will help prepare you for the pace of the exam.
Here are 5 tips for approaching the AP Statistics multiple choice questions:
-
Read the question and answer choices thoroughly
Carefully read each question and answer choice. Pay attention to what is being asked and the form of the correct answer, which is crucial for AP Stats MCQs.
-
Underline important information
When reading through the question stem, underline vocabulary, given values, function definitions, and the actual quantity the question is asking for. This will help you key in on the important aspects of the question. When you come across a vocabulary word, stop and analyze what it means. For example, if the question says “median,” take a moment to think about what that means in statistics.
-
Eliminate answer choices
Sometimes you can immediately eliminate an answer choice because it does not fit what the question is asking for. Cross out any such choices in your test booklet. For example, if the question asks you to interpret a p-value, you can eliminate choices that do not mention a null hypothesis.
-
Keep moving
If you do not immediately know how to solve a problem, skip it and return later. The AP Statistics exam is a timed test. Don’t waste time on questions you do not know until you answer the ones you do know. Fold the corner of the page in your question booklet to mark the pages you need to come back to. If there is time at the end of the exam, revisit the pages and questions you marked.
-
Read the question again
Before finalizing your answer, double-check what is being asked. This is particularly helpful in avoiding mistakes in AP Stats MCQs.
AP Statistics Multiple-Choice Examples
To give you a feel for the types of questions you will encounter in the AP Statistics multiple choice questions section, here are a few sample exam-like questions you’ll see:
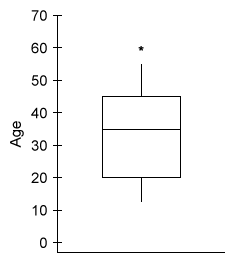
A random sample of 200 video game players was selected, and the age of each player was determined. According to the boxplot below, what is the approximate interquartile range (IQR) of the ages?
- 20
- 25
- 35
- 55
- 60
Explanation:
This is an “interpret graphs” question from Unit 1. There are a couple of things to note:
- AP Statistics questions almost always include a context, so you’ll need to carefully read the question and pick out key information. Some information is important, but other data can be irrelevant or misleading.
- Interpretation of graphs is very important for statistics and is one of the key skills you will need to master to do well on the exam. You will definitely see a graph on the exam, so make sure you are familiar with each type mentioned in the course.
- A box plot is a graph of a distribution of data based on a 5-number summary: minimum, first quartile (Q1), median (2nd quartile), third quartile (Q3), and maximum.
- Quartiles divide a distribution into 4 quarters, each holding about 25% of the data. Consider that quartiles may include outliers (data values outside the whiskers of a boxplot) as part of the distribution.

The interquartile range (IQR) measures the range of the middle 50% of the data in a distribution and is equal to the difference between the 3rd quartile (Q3) and the 1st quartile (Q1).
IQR = Q3 - Q1
On a boxplot, these 2 values form the outside edges of the "box." The edges of the given boxplot are approximately 45 (Q3) and 20 (Q1), so the IQR is 45 − 20 = 25.
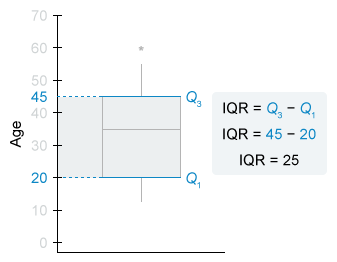
The approximate IQR of the ages is 25. Therefore, the correct answer is (b) 25.
A state is interested in knowing its citizens' opinions on a proposed tax increase on tobacco-based products. The Department of Health Services surveyed a random sample of citizens whose highest level of education is a high school diploma, a bachelor's degree, or a graduate degree. A total of 400 citizens responded with their highest level of education and whether they favor or oppose the tax increase. The results are shown in the table below.
| High level of education | |||||
| High school diploma | Bachelor's degree | Graduate degree | Total | ||
| Opinion on tax increase | Favor | 30 | 42 | 49 | 121 |
| Oppose | 160 | 108 | 11 | 279 | |
| Total | 190 | 150 | 60 | 400 | |
Which of the following statements about a randomly chosen person from these 400 citizens is true?
- If a person favors the tax increase, he or she is more likely to have a bachelor's degree as the highest level of education than to have only a high school diploma.
- If a person opposes the tax increase, he or she is more likely to have a postsecondary (bachelor's or graduate) degree as the highest educational level than to have only a high school diploma.
- The person is more likely to favor the tax increase if he or she has only a high school diploma as the highest educational level than if he or she has a postsecondary degree (bachelor's or graduate).
- The person is more likely to have only a high school diploma as the highest educational level than to have a postsecondary degree (bachelor's or graduate).
- The person is more likely to favor the tax increase than to oppose the tax increase.
Explanation:
This is a “contingency table" question from Unit 2. Contingency table questions involve simple calculations and are more focused on concepts. Typically, they involve navigating the difference between joint relative frequencies (values in individual cells divided by the table total) and conditional relative frequencies (values in individual cells divided by row/column totals). You'll need to carefully read the question and pick out key terms (“If, then”) that indicate particular types of relative frequencies or probabilities.
The answer choices all require a comparison of the likelihood (probability) of 2 events from the given table. To find the probability P of an event, use the following formula:
- Analyze the probabilities of each choice to determine which statement is true. If 2 probabilities have the same number of possible outcomes, it is necessary to compare only the desired outcomes.
- Notice in the "favor" row that there are more people with bachelor's degrees than with high school diplomas as their highest level of education.
- The number of people with a bachelor's degree (42) represents a greater proportion of those who favor the tax increase (121) than does the number of people with only a high school diploma (30).
Therefore, the correct answer is (a).
An insurance company surveyed each of its 130 employees to determine the proportion who donate to charitable organizations. Which of the following statements is true?
- The data from this survey should not be used because it is an observational study.
- It is necessary to use a confidence interval in order to estimate the proportion of employees who donate to charity.
- It is not necessary to use an inference procedure to determine the proportion of employees who donate to charity because the survey was a census of all employees.
- The result of this survey can be used to prove that working for the company causes employees to donate to charity.
- The sample of employees was not selected randomly, so the survey will not provide useful information.
Explanation:
This is a question from Unit 3, where questions do not involve calculations. Instead, interpret the way data collection influences what can and cannot be said about a population. It is critical to know the vocabulary terms for concepts such as sampling methods and experimental designs. Here are a few steps to follow if you face questions like this on the exam:
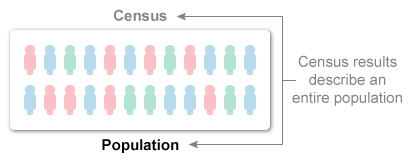
- A population is all the individuals of a specific group (ex. U.S. citizens, customers of an ice cream shop).
A census collects data from an entire population to draw conclusions about the population. Any result from a census also describes the population. There is no need to make inferences about the population.
- It is known that the insurance company surveyed each of its 130 employees, so they conducted a census of all employees.
Therefore, the statement that is true is (c): It is not necessary to use an inference procedure to determine the proportion of employees who donate to charity because the survey was a census of all employees.
A tutoring company prices lessons in groups of 10 lessons. The probability distribution of X, the number of lessons sold to a single customer, is summarized in the table below.
| X = the number of lessons | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| Probability | 0.15 | 0.25 | 0.30 | 0.20 | 0.10 |
The expected value of the probability distribution of X is 28.5 and the standard deviation is 11.95. There is a fixed cost of materials and advertising for the lessons. The profit Y, in dollars, for a single customer can be predicted by Y = 25X − 50. What is the standard deviation of Y ?
- $248.75
- $298.75
- $348.75
- $662.50
- $700.00
Explanation:
Unit 4 questions are mostly pure mathematics. All of the formulas from Unit 4 can show up on the exam, and there are several things to keep in mind for these questions:
- They allow the most creativity. Typically, they can be solved in many ways. If you find 1 method that you know doesn't work, try thinking about the question in another way.
- They are the most mathematical and require the most practice.
- They receive the lowest scores but represent a large portion of the test. Try doing as many practice questions as you can to be prepared.
Now, let's solve this problem with these pointers:
- A linear transformation of a random variable X is a transformed random variable Y formed by multiplying every value of X by a constant b and then adding another constant a (Y = a +bX)
The standard deviation (SD) of a linearly transformed random variable Y is equal to the SD of the original variable X multiplied by the absolute value of the constant b.
- It is given that the profit Y, in dollars, for a single customer can be predicted by the equation Y = 25X − 50, so Y is a linear transformation of X with a multiplicative constant of 25.
Plug the value of b (25) and the standard deviation of X (σX = 11.95) into the formula for the SD of a linear combination and solve for the standard deviation of Y (σY).
Therefore, the standard deviation of Y is $298.75. The correct answer is (b).
How to practice AP Statistics Multiple-Choice Questions
Use a reliable MCQ question bank to take timed practice tests and hone your time-management and precision skills. You can choose from the College Board®'s database of past questions, as well as UWorld's AP Statistics Exam Prep resources for best practice problems and tests. For consistent improvement, regularly attempt AP Stats MCQ practice sessions.

Frequently Asked Questions (FAQs)
How many multiple-choice questions are there on the AP Stats exam?
There are 40 MCQs on the AP Statistics exam.
How are the AP Stats multiple-choice questions graded?
The multiple-choice questions are scored by machines and simply based on whether a selection is correct or incorrect.
How long is the MCQ section of the AP Statistics exam?
The time allotted for the multiple-choice section of the AP Statistics exam is 1 hour 30 minutes.
When can I get multiple-choice questions from past AP Statistics exams?
The College Board releases past exam questions that can be downloaded.
References
- AP Statistics Course and Exam Description. (2020). apcentral.collegeboard.org. Retrieved on December 19, 2024 from https://apcentral.collegeboard.org/media/pdf/ap-statistics-course-and-exam-description.pdf
- AP Statistics. (n.d.). apcentral.collegeboard.org. Retrieved on December 19, 2024 from https://apstudents.collegeboard.org/courses/ap-statistics/assessment
Read More About the AP Statistics Exam
Answering FRQs doesn’t have to be tough! Learn how to approach AP Statistics free-response questions and get sample questions to help you succeed.
AP Statistics Study Plan & TipsDo you want to get a 5 on your AP exams? Check out our study plan & tips, written by industry experts, with resources to help you ace the AP Statistics exam.
AP Statistics Exam FormatConfused about the AP Statistics exam format? This article breaks down the format, types of questions, and more for quick reference.
Best AP Statistics Study Guide ComparisonDiscover expert insights into Kaplan, Barron's, Princeton Review, and UWorld. Learn how each resource compares to help you choose the best fit.
Best AP Statistics Prep Course ReviewSearching for top AP Statistics prep courses? Read this review to compare the best courses and choose the perfect one for your success.
How to Self-Study for AP StatisticsWant to ace AP Statistics on your own? Follow this expert self-study guide with tips, tricks, and tools to prepare effectively for the exam.