AP® Statistics Equation and Formula Sheet
The AP® Statistics Formula Sheet will be one of your most important tools for success on the AP Statistics exam. In order to get an edge in your preparation for the exam, it is a great idea to familiarize yourself with the formula sheet beforehand. Here we will describe everything you need to know about the formula sheet in detail.
What is AP Statistics Formula Sheet and Tables
The AP Statistics Formula Sheet and Tables includes formulas and probability tables that you will need to solve both the multiple-choice and free-response questions on the exam. The formulas cover all units of the course curriculum except Unit 3 (Collecting Data), which does not require formulas. The tables provide left-tailed or right-tailed areas under the normal distribution curve, the t-distribution curve, and the chi-square distribution curve.
It is technically possible to solve every question on the AP Statistics exam using just the formulas on the formula sheet, algebra, and the probability tables. But the formulas on the sheet won’t be helpful if you do not already have a solid understanding of the course content. Plus, many problems are better suited for calculators than using the formulas. Still, along with the material you learn from your AP Statistics course, learning about each of the formulas and tables will help you be more efficient and better understand the material on the exam.
In this guide, we will cover what is included with the AP Statistics Formula Sheet and Tables generally, as well as go over each individual formula in detail. In addition, we will go over many questions you may have about the formulas and table sheet, including what formulas are NOT included and so should be memorized.
Descriptive Statistics
The first section of the formula sheet provides the formulas for descriptive statistics from Unit 1 (Exploring One-Variable Data) and Unit 2 (Exploring Two-Variable Data). It is rare to use these formulas directly on questions, especially for multiple-choice questions. Moreover, if you do end up with a chance to calculate the statistics mentioned in this section, it will generally be easier to use a calculator. However, you will absolutely need to understand them and reference them for certain types of questions. Therefore, making yourself familiar with this section is still important.
|
x̅ =
1
/
n
∑ xi =
∑ xi
/
n
|
sx = √
1
/
n - 1
∑ (xi - x̅ )2 = √
∑ (xi - x̅ )2
/
n - 1
|
| ŷ = a + bx | y̅ = a + b x̅ |
|
r =
1
/
n - 1
∑ (
xi - x̅
/
sx
) (
yi - y̅
/
sy
)
|
b = r
sy
/
sx
|
Probability and Distributions
The second section of the formula sheet contains two important formulas from basic probability as well as several formulas to calculate the mean and standard deviation for any discrete random variable that will show up on the exam. Unlike the first section of the formula sheet, you will almost certainly be required to use these formulas for direct calculations. It is also less likely that you will be able to use calculators to automatically solve the questions involving these formulas. For that reason, it will be helpful to specifically practice using these formulas with AP Statistics practice questions.
P (A | B ) =
| Probability Distribution | Mean | Standard Deviation |
|---|---|---|
| Discrete random variable. X | µx = E (X ) = ∑ xi . P (xi ) | σx = √∑ (xi - µx )2 . P (xi ) |
|
If X has a binomial distribution with parameters n and p, then: P (X = x ) = (
n
/
x
)
px ( 1 - p )n-x where x = 0, 1, 2, 3, ..., n |
µx = np | σx = √np ( 1 - p ) |
|
If X has a geometric distribution with parameter p, then: P (X = x ) = (1 - p )n - x p where x = 1, 2, 3, ... |
µx =
1
/
p
|
σx =
√1 - p
/
p
|
Sampling Distributions and Inferential Statistics
The third section of the formula sheet contains meta formulas for the test statistics and confidence intervals on the AP Statistics exam. They are meta formulas because they do not make calculations directly, but are combined with specific information for each procedure. These meta formulas are incredibly important for the AP Statistics exam and you should understand them deeply both on a conceptual level and as be able to use them to generate the test statistics and confidence intervals for the exam.
|
Standardized test statistic:
statistic - parameter
/
standard error of the statistic
|
| Confidence interval: statistic ± (critical value) (standard error of the statistic) |
|
Chi-square statistic: χ2 = Σ
(observed - expected)2
/
expected
|
The information that can be combined with these formulas is given in the following parts of this section. They also contain general information important for understanding the sampling distributions of the important statistics on the example. For example, for procedures involving sample proportions:
| Random Variable | Parameters of Sampling Distribution | Standard Error of Sample Statistic |
|---|---|---|
| For one population: p̂ |
µp̂ = p σp̂ = √
p ( 1 - p )
/
n
|
Sp̂ =√
p̂ (1 - p̂ )
/
n
|
|
For two populations: p̂ 1 - p̂ 2 |
µ p̂ 1 - p̂ 2 = p1 - p2
σ p̂ 1 - p̂ 2 = √
p1 ( 1 - p1 )
/
n1
+
p2 ( 1 - p2 )
/
n2
|
S p̂ 1 - p̂ 2 = √
p̂1 ( 1 - p̂1 )
/
n1
+
p̂2 ( 1 - p̂2 )
/
n2 when p1 - p2 is assumed: S p̂ 1 - p̂ 2 = √ p̂c ( 1 - p̂c ) (
1
/
n 1
+
1
/
n 2
) where p̂c =
X 1 + X 2
/
n 1 + n 2
|
Probability Tables
Included with the formula sheet are tables that provide probabilities for the normal distribution, t-distribution, and the chi-square distribution. The probabilities these tables provide are different for each distribution, based on their use on the AP Statistics exam. These tables are used to calculate certain probabilities, mostly probabilities over intervals and p-values. However, the information in these tables can also be found using a calculator.
Should I use the probability tables included with the formula sheet or should I use a calculator?
Many students prefer calculators, but it’s really a personal preference. Calculators can give more information, but those good with tables may find they are faster. You really should be familiar with both. A calculator can always fail, but it will give the most precise results. Conversely, using a table may not be easy, but it is a great way to learn the content of the course.
AP Statistics Formula Sheet & Tables
Sample Mean
In Words: The left side of the equation is an x with a “bar” (line above the x) that represents the sample mean, while the right side of the equation is equal to the sum of the data divided by the number of data points (n ).
Description: This sample mean is the most important statistic on the AP exam. It represents the “center” or “average” of a set of data.
Application on AP Exam: It is unlikely that you will need this formula for calculation. This formula is conceptually important – think the central limit theorem, sampling distributions, t-tests, and other important topics. The formula is also useful for understanding how certain manipulations affect the sample mean. For example, how does multiplying the values in a dataset by 2 affect the sample mean?
Sample Standard Deviation
In Words: The left side of the equation is the sample standard deviation for the variable “x” (the subscript). The right side of the equation involves a lot of symbols, but it is straightforward if you take it in steps. (1) Subtract the sample mean from every value in the dataset, (2) Square the resulting values, (3) Add up the resulting values, (4) Divide the result by n – 1, and finally (5) Take the square root of the final result.
Description: This sample mean is the second most important statistic on the AP exam. It represents the “spread” or “variability” of a set of data.
Application on AP Exam: It is unlikely that you will need this formula purely for calculation. If it does come up, you should probably use a calculator instead of this formula. Most questions involving standard deviation will either give you the value of the standard deviation or otherwise require you to interpret features of the standard deviation.
Predicted value of the response variable (linear regression)
In Words: The left side of the equation represents the predicted value of the response variable in a simple linear regression model. It is denoted with a “y” with a so-called “hat” on top (the circumflex symbol). The right side of the equation provides the linear equation in which a given value of the explanatory variable (x ) is an input. The value of x is multiplied by the slope b and then y-intercept a is added.
Description: Simple linear regression is a procedure to predict a value of one variable (the response variable: y ) from the value of another variable (the explanatory variable: x ). This formula shows how prediction is done through simple linear regression – through plugging x into the equation for a line.
Application on AP Exam: One common question type on the AP exam is interpolation.. If the slope (a ) and y-intercept (b ).are given (and it’s likely they will be), then you should be able to turn the value of an explanatory variable x into the predicted value of the response variable y. Another type of question involves residuals. You will need to find the predicted value of y using a regression line, then compare to the observed value.
Point on the linear regression line
In Words: The left side of the equation (y with a bar) is the sample mean for a response variable y. The right side of the equation is the simple linear equation in which the mean of the explanatory variable is an input. The mean of x is multiplied by the slope b and then y-intercept a is added.
Description: This formula makes a conceptual point as well as being useful for calculation. The conceptual point is that the predicted value of y when x is equal to its mean is equal to the sample mean of y; that is, the regression line always goes through the point (x̄,ȳ ). This formula is also used for calculating the y-intercept of a linear regression line. If you have the sample mean of x, the sample mean of y, and the slope of the regression line, then this formula can be rearranged to isolate the value of a.
Application on AP Exam: The usage of this equation for the exam is as a reminder about the one point mentioned above – the point (x̄,ȳ ) is always on the regression line. Also, while such a question is highly unlikely, it is possible that you will need to calculate a y-intercept using this formula because it is a notable part of the curriculum.
Correlation coefficient
In Words: The left side of the equation (the “r”) is the correlation coefficient. The right side of the equation involves a lot of symbols, but like the standard deviation it is straightforward if you take it in steps. First, note that the expressions in the values are actually a type of z-score. (1) Calculate the z-scores for the data values for both variable x and variable y, (2) Multiply the paired z-scores, (3) Add up the resulting values, and finally (4) Divide the result by n – 1.
Description: The correlation coefficient, r, gives the direction and strength of the linear association between two quantitative variables.
Application on AP Exam: This is another formula you are unlikely to use directly on the AP exam. Similarly to the standard deviation, if it does come up, you should probably use a calculator instead of this formula. However, understanding this formula (especially the z-score interpretation) can help with several types of problems. For example, how does multiplying one variable by -1 affect the correlation coefficient?
Slope of the linear regression line
In Words: The left side of the equation (the “b”) is the slope of the linear regression line. The right side of the equation includes the correlation coefficient, multiplied by the ratio of the standard deviation of the response variable (y ) to the standard deviation of the explanatory variable (x ). Note: Keep in mind that the standard deviation in the numerator is the standard deviation for the values of y, NOT the standard deviation for the residuals of the linear regression.
Description: The slope of the linear regression line is the amount that the predicted value of the response variable y changes for each unit increase in x.
Application on AP Exam: There are several important applications of this formula on the AP exam. One that has come up several times is to understand the relationship between the correlation coefficient and slope. For example, if the correlation coefficient is positive, the slope must also be positive (and vice-versa). You should also be able to calculate the slope if given the correlation and the standard deviation of both variables involved in a regression.
General Addition Rule
In Words: The left side of the equation represents the probability of the “union” of two events A and B. The right side is the addition then subtraction of three separate probabilities: the probability of event A, and the probability of event B, and the “joint probability” of the events A and B. The joint probability of the events A and B is the probability that they both occur.
Description: The “union” of two events A and B is the probability that event A or event B (or both) will occur. One way to understand the union of events is as a Venn diagram.
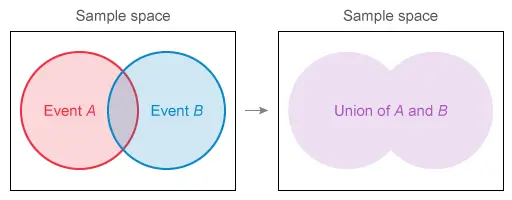
The general addition rule states that the purple area in the above diagram is equal to the red area plus the blue area, minus the section they overlap. This is because if the red and blue areas are added together, the central area is counted twice.
Application on AP Exam: The general addition rule (and a special case of the general addition rule – the addition rule for mutually exclusive events) is the main rule used to calculate the probability of the union of two events. It is also the only rule on the exam that explicitly relates the probability of a union to the joint probability, so any question that involves these quantities will likely use this formula.
Conditional Probability
In Words: The left side gives the conditional probability of A given B because the “|” symbol represents “given”. The right side includes the ratio of two probabilities: the joint probability of events A and B and the probability of event B.
Description: This is a definitional formula for the “conditional probability” that an event A occurs given that another event B has occurred.
Application on AP Exam: This formula is the main way to calculate conditional probabilities for the AP exam. If any question asks for the probability of an event that is “given” or similar language, then you will likely be able to use this formula to solve that question. Another application is that by rearranging this formula (multiplying both sides by P(B )), you will get another important formula for the test – the multiplication rule.
Mean of Discrete Random Variables
In Words: This formula gives the mean of a discrete random variable X. Consider that in order to use this formula, you have to know every possible value of X as well as their probabilities. The left two expressions are actually equivalent notation to represent the mean of a discrete random variable. The right side in steps says (1) Multiply each possible value of X by its probability,, and then (2) Add up the resulting values.
Description: The mean of a discrete random variable X describes the long-run average if the chance process resulting in X is repeated many times. It is also a measure of the center of the probability distribution of X.
Application on AP Exam: You should be able to calculate the mean of a discrete random variable X if the values of X as well as the probabilities are given in a table.
Standard Deviation of Discrete Random Variables
In Words: This formula gives the standard deviation of a discrete random variable X. Consider that in order to use this formula, you have to know every possible value of X, their probabilities, and the .The left side gives the notation for the standard deviation of a discrete random variable X (the subscript). The right side in steps says (1) Subtract the mean from each possible value of X, then square the resulting values, (2) Multiply these values by the corresponding probabilities, (3) Add everything up, and then (4) Take the square root of the result.
Description: Similarly to the standard deviation for a dataset, the standard deviation of a discrete random variable describes the “spread” or “variability” of that random variable.
Application on AP Exam: It is unlikely that you will need this formula purely for calculation. However, it may be possible for free response questions.
Probability Distribution of Binomial Random Variables
P (X = x ) = (
where x = 0, 1, 2, 3, …, n
In Words: The left side of the equation is notation for the probability that the binomial random variable X is equal to a specific value x. The right side of the equation has several parts. The large parentheses around n and x is referred to as the binomial coefficient and is called “n choose x”. The other parts involve multiplying the binomial coefficient by the probability of success (p) to the number of successes (x), then multiplying by the probability of failure (1 – p) to the number of failures (n – x).
Description: A binomial random variable counts the number of successes in n independent trials, in which each trial has a fixed probability p of a “success”. For a binomial distribution parameters n and p, the probability distribution gives the probability of any given possible number of successes x.
Application on AP Exam: You should be able to recognize a variable as binomial, and using given information, determine the n and p. It is possible you will need to plug those values into this formula to identify the probability.that the variable equals a given value x. It is unlikely you will need to then calculate the exact value, but if you do need to, it is easier to use a calculator.
Mean of Binomial Random Variables
In Words: It is possible to use the formula for the mean of a discrete random variable to calculate the mean of a binomial random variable. However, this formula specific to binomially distributed random variables is much easier to navigate. The left side is notation for the mean of a binomial random variable X. The right side is straightforward – multiply the number of trials n by the probability of success for each trial p.
Description: The mean of a binomial random variable X has the sample interpretation as the mean of any discrete random variable – it is the long-run average if the chance process resulting in X is repeated many times. It is also a measure of the center of the probability distribution of X.
Application on AP Exam: You should be able to recognize a variable as binomial, and using given information, determine the n and p. Given values of n and p, you should then be able to calculate the mean of a binomial random variable. Also, this formula can tell you about the relationship between the parameters and the value of the mean of a binomial random variable (e.g. increasing n increases the mean).
Standard Deviation of Binomial Random Variables
In Words: It is possible to use the formula for the standard deviation of a discrete random variable to calculate the standard deviation of a binomial random variable. However, the formula for the standard deviation of a binomial random is much simpler. The left side of the formula is notation for the standard deviation of a binomial random variable X. The right side in steps is (1) Multiply the sample n, the probability of success p, and the probability of “failure” (1 – p), then (2) Take the square root of the result.
Description: The standard deviation of a binomial random variable X has the sample interpretation as the standard deviation of any discrete random variable – it describes the “spread” or “variability” of that random variable.
Application on AP Exam: You should be able to recognize a variable as binomial, and using given information, determine the n and p. Given values of n and p, you should then be able to calculate the standard deviation of a binomial random variable. Also, this formula can tell you about the relationship between the parameters and the value of the standard deviation of a binomial random variable.
Probability Distribution of Geometric Random Variables
P (X = x ) = (1 – p )x – 1 p
where x = 1, 2, 3, …
In Words: The left side of the equation is notation for the probability that the geometric random variable X is equal to a specific value x. The right side of the equation states that for a given value of x, raise the probability of a failure (1 – p) to the x – 1 power, and then multiply by the probability of success p.
Description: A geometric random variable gives the number of the trial on which the first success in a sequence of independent trials occurs, where each trial has probability p of success. For a geometric variable with parameter p, the probability distribution gives the probability that the first success occurs on trial number x.
Application on AP Exam: You should be able to recognize a variable as geometric, and using given information, determine the value of p. It is possible you will need to plug those values into this formula to identify the probability.that the variable equals a given value x. You are more likely to need to calculate the exact value of the probability distribution of a geometric random variable than a binomial random variable.
Mean of Geometric Random Variables
In Words: It is possible to use the formula for the mean of a discrete random variable to calculate the mean of a geometric random variable. However, this formula is much easier to navigate. The left side is notation for the mean of a geometric random variable X. The right side is straightforward – calculate the inverse of p (that is, divide 1 by p).
Description: The mean of a binomial random variable X has the sample interpretation as the mean of any discrete random variable – it is the long-run average if the chance process resulting in X is repeated many times. It is also a measure of the center of the probability distribution of X.
Application on AP Exam: You should be able to recognize a variable as geometric, and using given information, determine p. Given the value of p, you should then be able to calculate the mean of a geometric random variable. Also, this formula can tell you about the relationship between the parameters and the value of the mean of a geometric random variable (e.g. increasing p decreases the mean).
Standard Deviation of Geometric Random Variables
In Words: It is similarly possible to use the formula for the standard deviation of a discrete random variable to calculate the standard deviation of a geometric random variable. However, this formula is much simpler. The left side of the formula is notation for the standard deviation of a geometric random variable X. The right side in steps is (1) Take the square root of 1 – p (the probability of failure on any trial), then (2) Divide the result by p.
Description: The standard deviation of a geometric random variable X has the sample interpretation as the standard deviation of any discrete random variable – it describes the “spread” or “variability” of that random variable.
Application on AP Exam: You should be able to recognize a variable as geometric, and using given information, determine p. Given the value of p, you should then be able to calculate the standard deviation of a geometric random variable. Also, this formula can tell you about the relationship between the parameter and the value of the standard deviation of a binomial random variable.
Standardized Test Statistic (general formula)
In Words: Actually, this formula is already in words.
Description: This meta formula demonstrates how most of the test statistics (for z-tests and t-tests) are constructed. In order to create the test statistic, you must input the value of the statistic calculated from the sample (for example, the sample mean), the parameter of interest (for example, mean of a population), and then divide the difference between those two quantities by the standard error of the sample statistic. One way to understand this formula is that it is a z-score, with “statistic” being the value of x, “parameter” being the mean, and “standard error of the statistic” being the standard deviation.
Note: The chi-square test statistic is an exception to this formula and does not follow it.
Application on AP Exam: This meta formula will show up many times on the AP exam. You will need to be able to use it to identify the test statistics for the majority of the tests on the exam.
Confidence interval (general formula)
In Words: Actually, this formula is already in words.
Description: This formula is another meta formula, used to construct other formulas rather than calculate anything itself. It shows how all confidence intervals on the AP Statistics exam are calculated. The values of “Statistic”, “critical value”, and “standard error of statistic” are all specific to the intervals for different parameters.
Application on AP Exam: This meta formula will show up many times on the AP exam. You will need to be able to use it to identify every confidence interval included with the AP exam.
Chi-square statistic (general formula)
In Words: The left side of the equation is the test statistic for chi-square tests – the chi-square statistic. The “observed” is the observed frequencies in each cell of a one-way or two-way table. The “expected” is the expected frequencies for those cells, which are calculated based on the given test. Note: The expected counts for each test are not provided for the chi-square tests, so you will have to memorize them in order to use this formula.
Description: The standardized test statistic formula mentioned above applies to the z-tests and the t-tests. However, there are three chi-square tests on the AP exam – the chi-square test for goodness of fit, the chi-square test for independence, and the chi-square test for homogeneity. The formula is the meta formula for those tests and is similar in that the values are specific to each test.
Application on AP Exam: This meta formula will show up on the AP exam, and maybe even more than once. You should be able to use it to identify the contribution of an individual cell of a table to the chi-square statistic. You should also be able to use this formula to calculate the chi-square statistic when the number of cells is low (e.g. 3).
Sampling Distributions for Proportions
| Random Variable | Parameters of Sampling Distribution | Standard Error of Sample Statistic | |
|---|---|---|---|
| For one population: p̂ |
µp̂ = p |
σp̂ = √
p ( 1 – p )
/
n
|
Sp̂ =√
p̂ (1 – p̂ )
/
n
|
|
For two populations: p̂ 1 – p̂ 2 |
µ p̂ 1 – p̂ 2 = p1 – p2 |
σ p̂ 1 – p̂ 2 = √
p1 ( 1 – p1 )
/
n1
+
p2 ( 1 – p2 )
/
n2
|
S p̂ 1 – p̂ 2 = √
p̂1 ( 1 – p̂1 )
/
n1
+
p̂2 ( 1 – p̂2 )
/
n2 when p1 – p2 is assumed: S p̂ 1 – p̂ 2 = √ p̂c ( 1 – p̂c ) (
1
/
n 1
+
1
/
n 2
) where p̂c =
X 1 + X 2
/
n 1 + n 2
|
Sampling Distributions for Means
| Random Variable | Parameters of Sampling Distribution | Standard Error of Sample Statistic | |
|---|---|---|---|
| For one population: X̅ |
µ x̅ = µ |
σ x̅ =
σ
/
√n
|
S x̅ =
S
/
√n
|
|
For two populations: X̅ 1 – X̅ 2 |
µ x̅ 1 – x̅ 2 = µ1 – µ2 |
σ x̅ 1 – x̅ 2 = √
σ1 2
/
n1
+
σ2 2
/
n2
|
S x̅ 1 – x̅ 2 = √
S1 2
/
n1
+
S2 2
/
n2
|
Sampling Distributions for Simple Linear Regression
| Random Variable | Parameters of Sampling Distribution | Standard Error of Sample Statistic | |
|---|---|---|---|
| For slope: b |
µ b = β |
σb =
σ
/
σx √n
where σx = √
Σ ( x i – x̅ ) 2
/
n
|
Sb =
S
/
Sx √n – 1
where S = √
Σ ( y i – ŷ i ) 2
/
n – 2
and Sx = √
Σ ( x i – x̅ ) 2
/
n – 1
|
Description: The rest of the formulas included with the formula sheet are arranged in three separate tables. These tables include a lot of information, so we will not go over the individual contents here. Instead, you should know that the left column describes the statistic (“Random Variable”) of interest, the second column gives the mean and standard deviation for the sample distribution of the statistic, and the third column gives the standard error of the sample statistic (the estimate of the standard deviation based on data).
Application on AP Exam: There are three main classes of questions on the AP exam that use these tables. The first class is questions asking for descriptions of the sampling distribution of certain statistics. For example, the question may ask you to provide the best description of the sampling distribution, including identifying the mean and the standard deviation of the distribution. These can involve calculating only one of the parameters (e.g. calculating the standard deviation) or calculating all of them along with the shape of the sampling distribution. The second class of questions are those involving standardized test statistics. Combining the standardized test statistic above with the information in these tables allows you to generate the test statistics for all of the z-tests and t-tests on the exam. For example, consider the one-sample t-test for a mean. The statistic is the sample mean, the parameter is the population mean, and the standard error of the statistic is the standard error of the sample mean.
| Random Variable | Parameters of Sampling Distribution |
Standard Error of Sample Statistic |
|---|---|---|
| For one population: X̅ |
µ x̅ = µ σx̅ =
σ
/
√n
|
S x̅ =
S
/
√n
|
Note: The final class of questions are those involving the general formula for a confidence interval. Information from these tables makes up the majority of z-intervals and t-intervals.
| Random Variable | Parameters of Sampling Distribution |
Standard Error of Sample Statistic |
|---|---|---|
| For one population: p̂ |
µ p̂ = p σp̂ = √
p ( 1 – p )
/
n
|
S p̂ =
√
p̂ ( 1 – p̂ )
/
n
|
z* = critical value from probability tables or calculator
Table A: Standard Normal Probability Table
Description: Table A gives the left-sided area (area from a value z to negative infinity) under the standard normal distribution curve. The standard normal distribution is a normal distribution with mean equal to 0 and standard deviation equal to 1. It can be used to describe probabilities for any normal distribution (not just the standard normal distribution) through the use of z-scores. It is also useful for finding the p-values for z-tests and the critical values for z-intervals.
Using Table A: To determine the area under the standard normal curve to the left of a value of z, consider that the rows of the table correspond to the “ones” and “tenths” place of the value of z, and that the columns correspond to the “hundredths” place of the value of z.
For example, suppose that you wish to determine the area to the left of z = 1.10. First, you should find the row that corresponds to a ones/tenths value of “1.1”. Second, find the column that correspond to the value “x.x0”. The intersection of this row and column is the left-tailed area (probability).
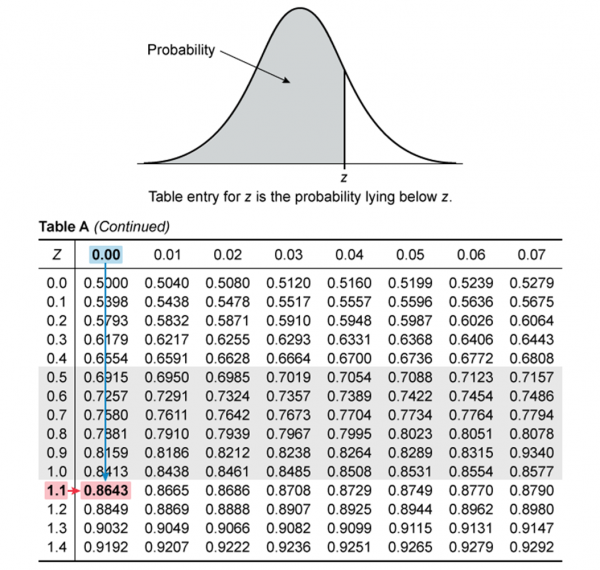
Note: It is also possible to use this table to determine the area (probability) to the right of a value of z. First find the left-tailed area, then subtract that area from 1. This is because the total area under the curve must be equal to 1.
Table B: t-Distribution Critical Values Table
Description: Table B gives the values (t-values) of the t-distribution that yield a right-tailed probability of a given value. There are actually many different t-distributions, depending on the value of the degrees of freedom df, so the table also includes the possible values of the degrees of freedom. Consider that the values given in this table are different from Table A. Table A is made up of probabilities, while Table B is made up of values of a t-distributed random variable.
Using Table B: To find a t-score with a certain probability lying above it (to the right of it), first identify the df of the t-distribution. The df is generally specific to the t-test or t-interval being performed, but is based on the sample size (e.g. n − 1). Second, identify the appropriate row for the df. Then, you can find the appropriate “Tail probability” by looking at the top of the table.
For example, suppose that you wish to determine the t-score from a t-distribution with a probability of .025 lying above it, for df = 11. First, you should find the row that corresponds to df = 11. Second, find the column that corresponds to the tail probability .025. The intersection of this row and column is the t-score.
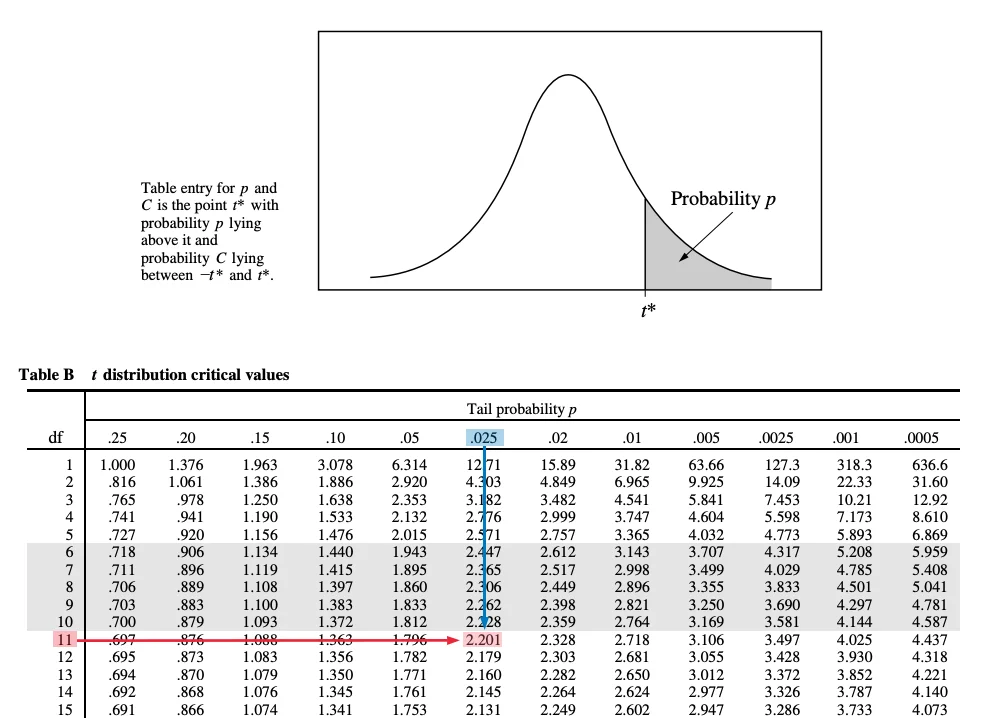
There is another use for Table B. At the bottom of the table, notice that each column is labeled with “Confidence level” percentages. This shows that Table B can also be used to find the critical values necessary to achieve given confidence levels. Critical values can be found for t-distributions of a given df value, or for the normal distribution (df = ∞). For example, a z-interval for a proportion is based on the normal distribution. The critical value for a 95% z-interval for a proportion can be found by identifying the ∞ row and the “95%” column at the bottom of the table.
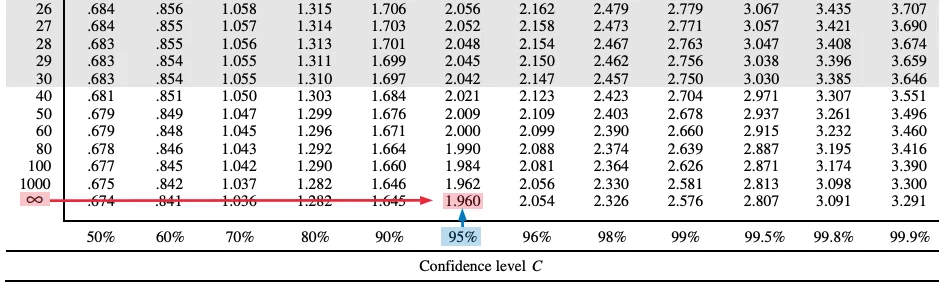
Table C: Chi-square Table
Description: Table C gives the values of the chi-square distribution that yield a right-tailed probability of a given value. Similarly to the t-distribution, there are many different chi-square distributions, depending on the value of the degrees of freedom df. Similarly to Table B, this table also includes the possible values of the degrees of freedom.
Using Table C: The procedure to find a chi-square value with a certain probability lying above it (to the right of it) is the same as the procedure for Table B. Note, however, that there is NOT a confidence level portion of the table for the chi-square distribution.
What formulas are not included with the AP Statistics formula sheet?
The AP Statistics formula sheet does not include all formulas you’ll need for the AP Statistics exam. Here is a list of statistics and rules on the AP Statistics exam you will need to memorize.
| Units | Formulas |
|---|---|
| Unit 1 |
|
| Unit 2 |
|
| Unit 3 |
|
| Unit 4 |
|
| Unit 5 |
|
| Unit 6 & 7 |
|
| Unit 8 |
|
| Unit 9 |
|
Read more about the AP Statistics Exam
A perfect study guide can help you score 5 easily! See what our experts advise on how to score high in AP Statistics with all the essential resources to succeed.
Want to know if AP Statistics is the right course for you? Our well-explained article can help you get a clear picture of the exam and make your exam prep easy!
Don’t let the AP Exam format confuse you. Our self-explanatory guide will help you easily understand the exam format—question types, topic weights, and more!
Looking for an easy-to-follow course and exam description for AP Statistics? See our guide for clear info on the AP Stats course—units, topics, and key concepts.