Prep for the Digital
PSAT/NMSQT® Exam

Get PSAT-ready & potentially qualify for National Merit® scholarships with our Digital SAT® prep course.
ARE YOU AN EDUCATOR?
Explore our College Readiness products for districts, schools, and teachers here

PSAT Success Starts with Practice

Whether you’re going after a National Merit Scholarship® or starting your Digital SAT exam prep early, we can help.

It’s simple–a digital test needs digital prep. Get comfortable with the format of the exam, discover opportunities for improvement, and progress through difficult concepts with comprehensive feedback on all of your answer choices—both correct and incorrect. You’ll gain the confidence and content knowledge needed to achieve a stellar score on the PSAT/NMSQT by practicing with exam-like Digital SAT questions.

Why Practice with UWorld Prep?

Practice with Exam-Like Questions

  • Hundreds of Digital SAT practice questions that mimic the real test build confidence and reduce anxiety.
  • Content that is designed to match or exceed the exam's level of difficulty, ensuring you feel self-assured on test day.

Practice with Exam-Like Questions

UWorld Digital SAT Question 1
UWorld Digital SAT Question 2
UWorld Digital SAT Question 3
  • Hundreds of Digital SAT practice questions that mimic the real test build confidence and reduce anxiety.
  • Content that is designed to match or exceed the exam's level of difficulty, ensuring you feel self-assured on test day.

Learn From Mistakes

UWorld Digital SAT Explanation 1
UWorld Digital SAT Explanation 2
UWorld Digital SAT Explanation 3
  • Learn the concepts needed to improve your score with our detailed answer explanations.
  • Enhance knowledge retention through our industry-leading illustrations.
  • Grasp complex ideas through our meticulously crafted, step-by-step problem-solving assistance.

Learn From Mistakes

  • Learn the concepts needed to improve your score with our detailed answer explanations.
  • Enhance knowledge retention through our industry-leading illustrations.
  • Grasp complex ideas through our meticulously crafted, step-by-step problem-solving assistance.

Study Smarter

  • Our score predictor and performance reports tell you where you stand and what you need to work on — saving you time and energy.
  • Decide how many practice questions you want to complete based on your schedule.
  • Build memory retention and recall by creating flashcards, highlights, and annotations to note what you think matters most.

Study Smarter

Select UWorld Digital SAT Questions
Create UWorld Digital SAT flashcards
  • Our score predictor and performance reports tell you where you stand and what you need to work on — saving you time and energy.
  • Decide how many practice questions you want to complete based on your schedule.
  • Build memory retention and recall by creating flashcards, highlights, and annotations to note what you think matters most.

Benefits of Taking the PSAT/NMSQT Exam

Scholarships

A strong PSAT/NMSQT score can qualify you for the National Merit Scholarship and other merit-based awards.

Dream School

Your score will help you plan your next steps after graduation, increasing your chances of admission to your dream school.

SAT Readiness

It can help you get a top score on the Digital SAT by identifying your strengths and weaknesses.

Start Your Free Trial Now

Try Our Digital SAT Sample Questions to Prep for PSAT/NMSQT

Go into test day fully confident that you have mastered the concepts on the PSAT by practicing with exam-like questions.
The exploration of dystopian and utopian societies is central in two of Aldous Huxley’s novels. In Brave New World, for example, the “happy” population of the dystopian society believes and desires whatever the government’s World Controller dictates, while in Island, Will Farnaby at first ______ against the island’s utopian society for personal profit but later experiences a change of heart.

Which choice completes the text so that it conforms to the conventions of Standard English?

  1. conspired
  2. had conspired
  3. conspires
  4. will be conspiring
Submit Next Question

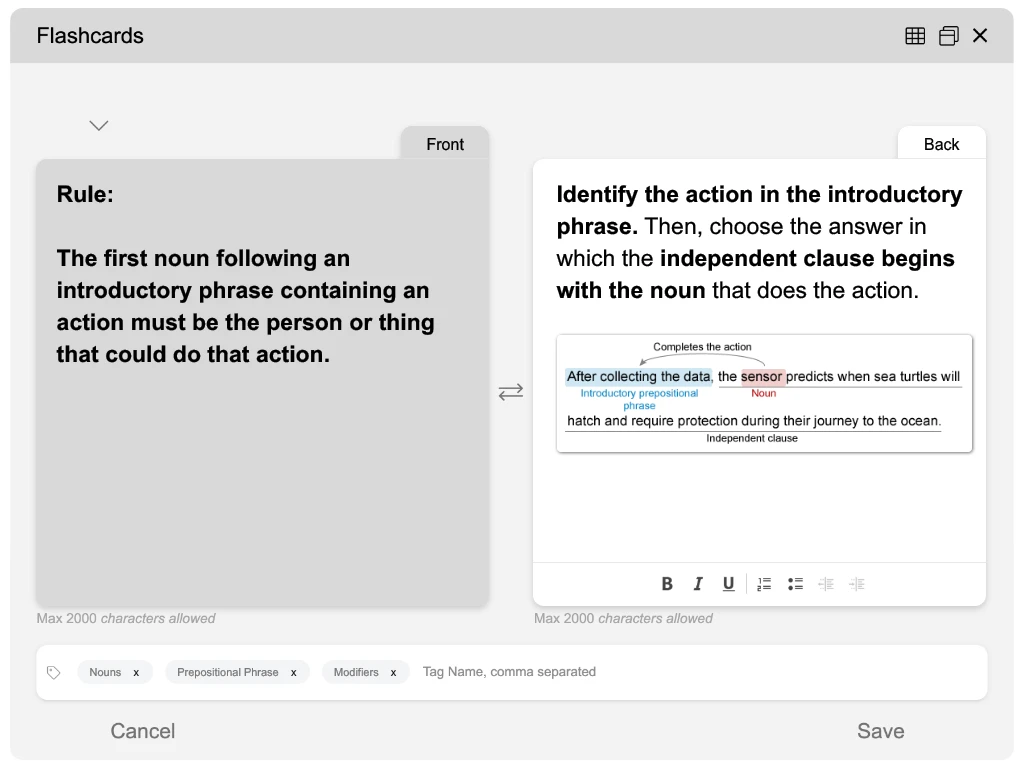
Rule: Unless a shift in time is indicated, verb tenses in a passage should match.

Identify the tense of the text’s verbs and select the answer that matches that tense.

Aldous Huxley on Utopia

The text includes present tense verbs, such as “is,” “thinks,” “desires,” and “dictates,” to describe actions in the present. Because the text doesn’t indicate a shift in time, the missing verb should also be in present tense.

“Conspires” is in the present tense, which matches the tense of the text’s other verbs. Therefore, the answer that conforms to the conventions of Standard English is conspires.

(Choices A, B, and D) These answers don’t use the present tense.

  • Choices A and B: “Conspired” and “had conspired” express actions occurring in the past, which doesn’t match the text’s use of present tense elsewhere.
  • Choice D: “Will be conspiring” expresses actions occurring in the future, which doesn’t match the text’s use of present tense to discuss the novels.

Things to remember:
Choose the answer that matches the tense expressed by other verbs in the passage.

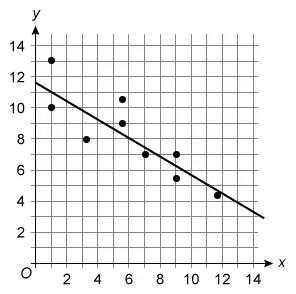
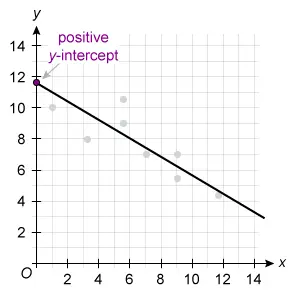
Two-Variable Data: Scatterplots and Models

The scatterplot shows the relationship between two variables, x and y. Of the following, which equation best represents the line of best fit shown?

  1. y = −11.7 − 0.6x
  2. y = −11.7 + 0.6x
  3. y = 11.7 − 0.6x
  4. y = 11.7 + 0.6x

Hint :

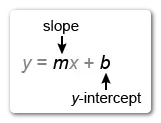
The equation of a line in slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.

Submit Next Question

The equation of a line in slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.

Graphs of linear functions

In each choice, the value of m is −0.6 or 0.6 and the value of b is −11.7 or 11.7. Therefore, it is possible to determine which equation best represents the line of best fit based on only the signs of the slope and y-intercept.

slope

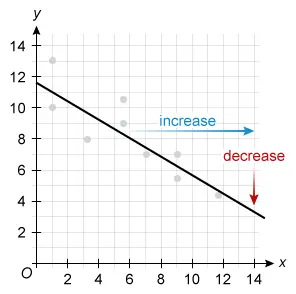
A line with positive slope increases from left to right.
A line with negative slope decreases from left to right.

The given line of best fit decreases from left to right, so its slope is negative.

Two-Variable Data: Scatterplots and Models

Therefore, the slope must be m = −0.6.

y-intercept

The y-intercept of a line is the y-value of the point where the line crosses the y-axis. The given line crosses the y-axis at a positive y-value, so its y-intercept is positive.

Two-Variable Data: Scatterplots and Models

Therefore, the y-intercept must be b = 11.7.

Plug m = −0.6 and b = 11.7 into slope-intercept form to get an equation of the line best fit y = −0.6x + 11.7. To match the form of the answer choices, rearrange the equation to get y = 11.7 − 0.6x.

(Choice A) y = −11.7 − 0.6x is incorrect because its y-intercept is negative (instead of positive).

(Choice B) y = −11.7 + 0.6x is incorrect because its slope is positive (instead of negative), and its y-intercept is negative (instead of positive).

(Choice D) y = 11.7 + 0.6x is incorrect because its slope is positive (instead of negative).

Things to remember:

  • A linear equation in slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
  • A line with a positive slope is increasing, and a line with a negative slope is decreasing.
Antonio Márez y Luna, the protagonist of Rudolfo Anaya’s 1972 novel Bless Me, Ultima, is on a spiritual journey of self-discovery, a story arc that, in Anaya’s work, is not ______: many of his narratives illustrate similar explorations of identity.

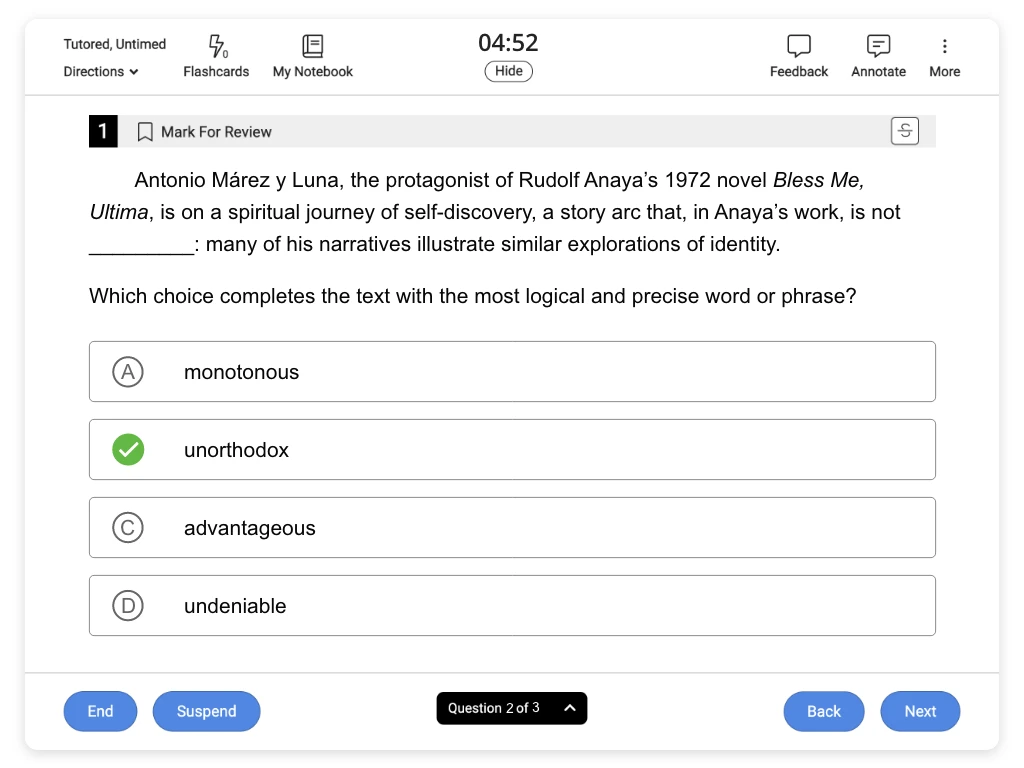
Which choice completes the text with the most logical and precise word or phrase?

  1. monotonous
  2. unorthodox
  3. advantageous
  4. undeniable
Submit Next Question

Try each word in the blank and use the process of elimination to determine which word has a meaning that works best given the context of the text.

The text states that many of Anaya’s narratives (stories) include a character exploring their identity and references one of his novels as an example. Notice that the word immediately before the blank is “not.” This signals that Anaya’s story arcs are the opposite of the word that completes the sentence.

Icons
Because the prefix “un-” means not, when “not” and “un-” are used together, they cancel each other out. (Ex. Not unordinary = ordinary)
(Choice A) monotonous = lacking in variety This answer suggests that Anaya’s stories are not all the same. However, the text reveals that many of Anaya’s story arcs are similar, which means they could be described as lacking variety.
(Choice B) unorthodox = contrary to what is expected or traditional This answer suggests that Anaya’s story arc is expected. The text says that “many of his narratives illustrate similar explorations” as the story in Bless Me, Ultima; therefore, this answer is correct.
(Choice C) advantageous = favorable; beneficial This answer suggests that Anaya’s stories are not favorable. However, the text doesn’t provide any details about whether Anaya’s story arcs are beneficial.
(Choice D) undeniable = plainly true; certain This answer suggests that Anaya’s stories are not certain, but this isn’t supported by the statement that his other works explore similar themes.

Things to remember:
Eliminate answers not supported by the text’s discussion.

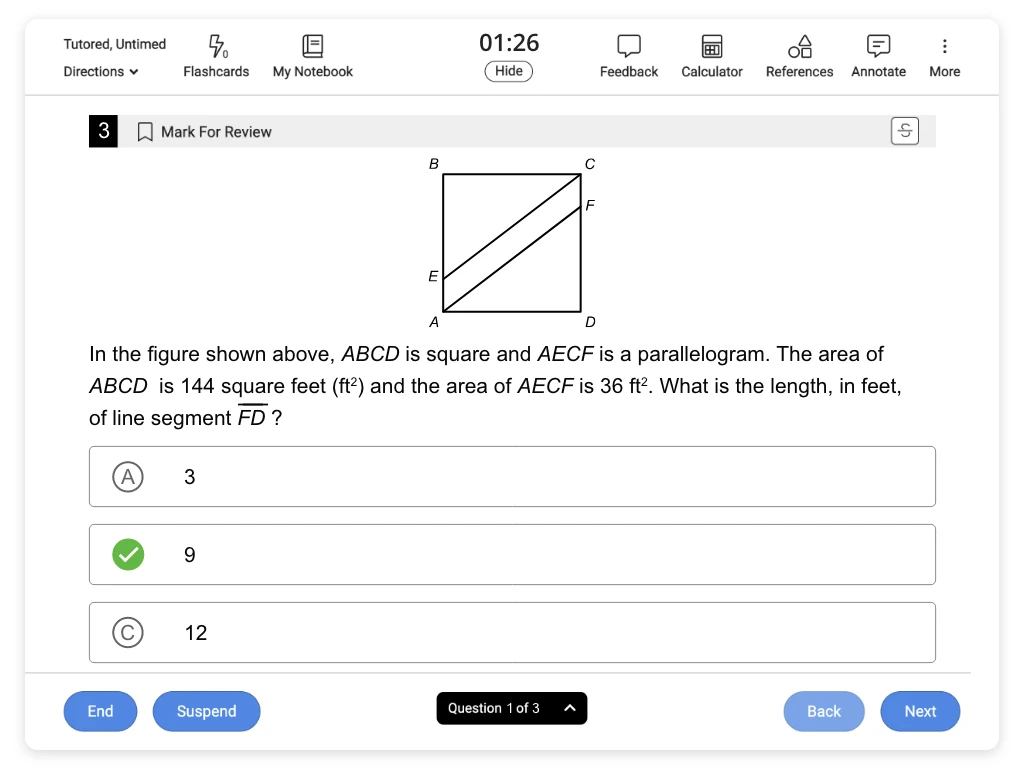
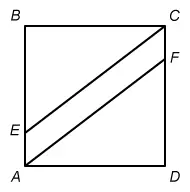
Area and length

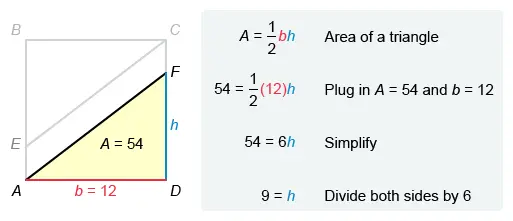
In the figure shown above, ABCD is a square and AECF is a parallelogram. The area of ABCD is 144 square feet (ft2) and the area of AECF is 36 ft2. What is the length, in feet, of line segment FD ¯¯¯¯ ?

  1. 3
  2. 9
  3. 12
  4. 15

Hint :

Segments  FD ¯¯¯¯ and AD ¯¯¯¯ are the sides of triangle AFD. Segment AD ¯¯¯¯ is also a side of square ABCD.

Submit Next Question

Notice that FD ¯¯¯¯ and AD ¯¯¯¯ are the legs of right triangle AFD, and that segment  AD ¯¯¯¯ is also a side of square ABCD. Use the given area of square ABCD to find the length of AD ¯¯¯¯ .

The area of parallelogram AECF is also given. Use the given areas to find the area of triangle AFD, and then use the area of the triangle to find the length of  FD ¯¯¯¯ .

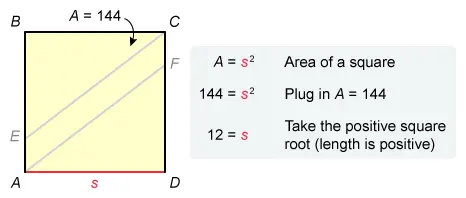
length of  AD ¯¯¯¯

The formula for the area of a square is A = s2, where s is the side length. It is given that the area of square ABCD is 144 ft2, so plug A = 144 into the formula and solve for s.

Additional Topics in Math, Area and Volume

Square ABCD has side length s = 12, so the length of  AD ¯¯¯¯ is 12 ft.

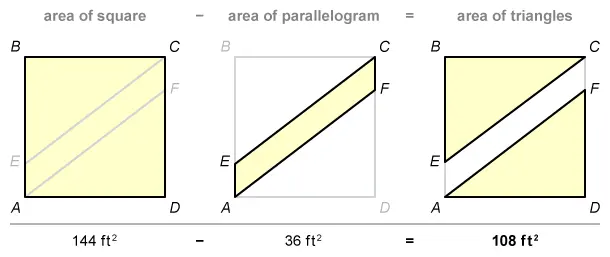
area of triangle AFD

The combined area of triangles AFD and CEB is equal to the area of square ABCD minus the area of parallelogram AECF.

The given area of square ABCD is 144 ft2 and that of parallelogram AECF is 36 ft2. Subtract to find that the combined the area of triangles ADF and CEB is 108 ft2.

Additional Topics in Math, Area and Volume

Triangles AFD and CEB are congruent (proof), so they have equal areas. Therefore, the area of triangle AFD is half of the combined area.

Divide 108 by 2 to find that the area of triangle AFD is 54 ft2.

Now use the length of  AD ¯¯¯¯ (12) and the area of triangle AFD (54) to solve for the length of  FD ¯¯¯¯ .

The formula for the area of a triangle is A = 1 2 bh where b is the length of the base and h is the height. Let AD ¯¯¯¯ be the base and let FD ¯¯¯¯  be the height. Plug A = 54 and b = 12 into the area formula and solve for h.

Additional Topics in Math, Area and Volume

The value of h is 9, so the length of FD ¯¯¯¯ is 9.

(Choice A) 3 is the length of the shorter side of parallelogram AECF. This may result from mistakenly finding the length of FC ¯¯¯¯ (instead of FD ¯¯¯¯ ).

(Choice C) 12 is the side length of square ABCD. This may result from mistaking the length of FD ¯¯¯¯ to be equal to the length of AD ¯¯¯¯ , but FD ¯¯¯¯ is not a side of square ABCD.

(Choice D) 15 is the length of the hypotenuse of triangle AFD. This may result from mistakenly finding the length of  AD ¯¯¯¯ (instead of FD ¯¯¯¯ ).

Things to remember:

  • The formula for the area of a square is A = s2, where s is the side length.
  • The formula for the area of a triangle is  A = 1 2 bh , where b is the length of the base and h is the height.
  • If two right triangles have congruent hypotenuses and a pair of congruent legs, the triangles are congruent (hypotenuse-leg congruence theorem).
  • If two triangles are congruent, they have equal areas.
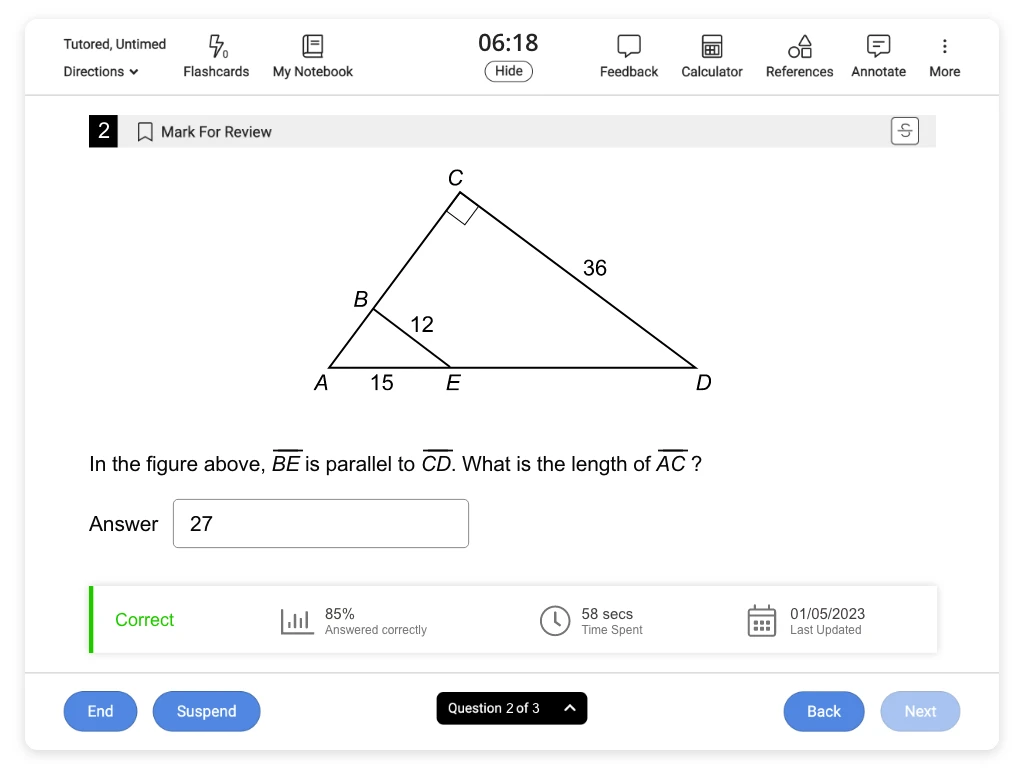
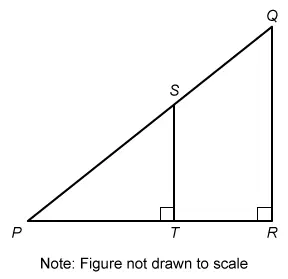
Right triangles and trigonometry

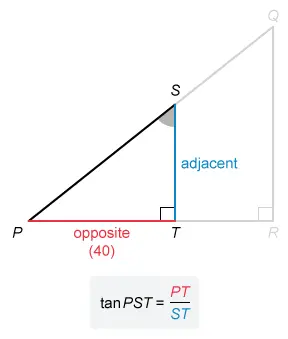
In the figure above, PQR and PST are right triangles and the tangent of angle PQR is 1.25. If PT = 40, what is the length of segment ST ?

Answer:

Hint :

The tangent of an acute angle in a right triangle is equal to the following ratio of side lengths:

tangent (tan)
opposite leg adjacent leg
Submit
Correct Answer : 32

The tangent of an acute angle in a right triangle is equal to the following ratio of side lengths:

tangent (tan)
opposite leg adjacent leg

The length of segment PT is given (40), and the question asks for the length of segment ST. No other side lengths are given, so it is not possible to use the Pythagorean theorem or a proportion of similar triangles to find ST.

However, PT and ST are the opposite and adjacent sides of angle PST. Therefore, if the tangent ratio of this angle is found it will be possible to write an equation to solve for ST.

Additional Topics in Math, Trigonometry

Notice that right angles PRQ and PTS are congruent corresponding angles. If two lines form congruent corresponding angles when cut by a transversal, then the lines are parallel. That means QR ¯¯¯¯ and ST ¯¯¯¯ are parallel.

Therefore, corresponding angles PQR and PST formed with transversal PQ ¯¯¯¯ must also be congruent.

Additional Topics in Math, Trigonometry

Congruent angles have equal trigonometric ratios, so the tangent of angle PQR must be equal to the tangent of angle PST. It is given that the tangent of angle PQR is 1.25, so the tangent of angle PST must also be 1.25.

Therefore, the ratio of opposite side PT to adjacent side ST is 1.25. Set tan PST equal to PT ST  and plug in the known values, then solve for ST.

tan  PST = PT ST Set tan PST equal to ratio of side lengths
1.25 =   40 ST Plug in tan PST = 1.25 and PT = 40
1.25 ST = 40 Multiply both sides by ST
ST = 32 Divide both sides by 1.25

The length of segment ST is 32.

Things to remember:

  • Three main trigonometric ratios are defined for an acute angle in a right triangle: sine, cosine, and tangent. Each is equal to a specific ratio of side lengths.
sine (sin) cosine (cos) tangent (tan)
opposite leg hypotenuse adjacent leg hypotenuse opposite leg adjacent leg
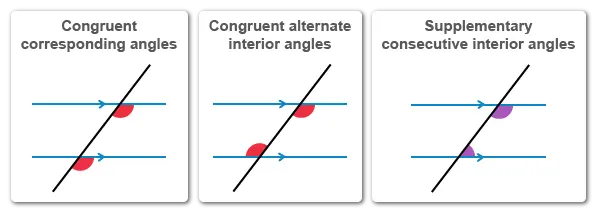
  • When parallel lines are intersected by a transversal, the following pairs of angles are formed:
Geometry, Lines and Angles

Practice Sample Questions Anywhere at Any Time

With the UWorld College Prep mobile app, you can practice exam-like questions from anywhere. Your results are automatically saved and synced across devices, allowing you to easily track your progress. Download the app today!
Apple App Store
Google Play Store
Get UWorld Digital Mobile App
With the UWorld College Prep mobile app, you can practice exam-like questions from anywhere. Your results are automatically saved and synced across devices, allowing you to easily track your progress. Download the app today!
Apple App Store
Google Play Store

Frequently Asked Questions (FAQs)

PSAT stands for Preliminary Scholastic Aptitude Test. Like the SAT and Digital SAT, the PSAT is administered by the College Board®. There are three versions of the PSAT: the PSAT™ 8/9, the PSAT™ 10, and the PSAT/NMSQT. All versions of the PSAT assess college readiness and consist of two parts: a Reading and Writing Section, as well as a Math Section. Additionally, the PSAT/NMSQT can qualify students for the National Merit Scholarship Program.
Taking the PSAT/NMSQT gives students valuable insight into the format and content of the SAT and Digital SAT. It supports them by highlighting specific areas that need improvement to achieve a high score on these college entrance exams. It also opens doors to scholarships, such as the National Merit Scholarship. Qualifying for this highly esteemed award provides a notable competitive advantage in the realm of college admissions, positioning students for substantial financial awards. In addition to the $2500 National Merit Scholarships, students who earn high scores on college entrance exams also have the opportunity to earn Corporate-sponsored Merit Scholarship awards, as well as College-sponsored Merit Scholarship awards.
The total duration of the exam is 2 hours and 14 minutes, with additional time for breaks, and is conducted during the regular school day.

Preparing for the PSAT/NMSQT involves a combination of studying, practicing, and familiarizing yourself with the test format. Start by becoming familiar with the types and difficulty-level of questions on the exam. You can do this with a prep resource that provides practice questions that mimic those on the real exam. A quality resource should also help you figure out where you stand with PSAT/NMSQT prep so you can focus on any problem areas and develop stronger learning connections in the process. UWorld’s Digital SAT QBank, with its immediate feedback and detailed answer explanations, is a great resource for this.

Taking the time to look closely at performance reports is also helpful; doing so can help you look for any question types you may consistently miss or content areas you may need to focus on. UWorld performance dashboards can help with this, too, providing data students can use to analyze mistake patterns quickly.

Time management is crucial on standardized tests, so practicing test-taking strategies such as the process of elimination and text annotation can help you learn to answer questions quickly and accurately. The practice exams provided with UWorld’s Digital SAT prep simulate real test conditions, allowing students to get used to the exam’s time constraints while practicing a variety of testing strategies. 
The exam is given in October, and most students take the PSAT/NMSQT during their sophomore or junior year of high school. To be eligible for the National Merit Scholarship Program, students must take the PSAT/NMSQT during their junior year of high school.
The best way to prepare for a digital PSAT exam is to practice with digital preparation tools. UWorld’s Digital SAT prep uses the same format and question types as the digital PSAT exam, so it is an excellent resource for PSAT preparation.

There are a few notable differences and similarities between the PSAT/NMSQT and the Digital SAT.

  1. Scoring Structure: Different
    The PSAT/NMSQT has a score range of 320 to 1520. The Digital SAT is scored from 400 to 1600.
  2. Test Administration: Different
    The SAT exam is offered many times throughout the year, and there is no limit on the number of times you can take it. The PSAT/NMSQT, however, is only offered once a year, and students can only take it up to three times. 
  3. Duration: Same
    The PSAT/NMSQT and the Digital SAT both take 2 hours and 14 minutes.
  4. Format and Topics: Same
    Both exams are divided into two distinct sections: (1) the Reading and Writing Section, and (2) the Math Section. Both exams also have a total of 98 questions. The tested subjects and question types are consistent across both tests, as well. 
The highest PSAT score you can get on the PSAT/NMSQT test is a 1520. To be considered for a National Merit scholarship, students must earn a score in the 99th percentile.
The average PSAT/NMSQT score is a 920. A score of 1210 ranks in the 90th percentile, and, to score in the 99th percentile, a student must earn a 1450 or above.

Looking for Digital SAT Prep?

Please provide the marketing pitch for the Digital SAT product page.

Digital SAT Online Prep Course

Related Articles

Scroll to Top