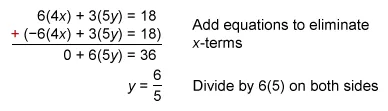What Algebra Is on the SAT?
SAT® algebra questions focus on foundational algebraic reasoning, linear equations, inequalities, systems, functions, and word problems that require translating real scenarios into mathematical expressions. You will also see questions involving quadratic equations, graphs, and relationships between variables. SAT algebra plays a major role in the Math section, so consistent SAT algebra practice is essential. A strong understanding of these concepts will make algebra SAT math questions feel more predictable and manageable.
SAT Algebra Question Types
SAT algebra questions can appear in multiple formats, including multiple choice and grid-in response items. You may solve linear equations, interpret graphs, compare expressions, or apply algebra to real-world scenarios. Since some SAT algebra 2 questions may also appear, practicing a wide range of algebra skills helps you feel confident on test day. Consistent SAT algebra practice prepares you to recognize patterns and approach each problem with the right strategy.
Linear Equations in One Variable
These SAT algebra questions require solving equations that contain only one variable. You may be asked to simplify expressions, isolate the variable, or rewrite the equation in a different form. These items often involve operations like distributing, combining like terms, or handling rational expressions. Strong fluency with these basics helps you move quickly through SAT algebra practice questions.
Linear Equations in Two Variables
Some algebra SAT math questions include equations with two variables that represent a relationship rather than a single value. These problems may ask you to interpret a slope, rewrite an equation in a different form, or analyze relationships between coefficients. Knowing how variables interact helps you understand the behavior of a line or compare two expressions.
Linear Functions
Questions in this category focus on identifying and interpreting functions that represent linear relationships. You may work with graphs, tables, or algebraic rules. Linear function items often measure your ability to understand Rate of Change, Intercepts, and how altering a coefficient influences the function. These SAT algebra problems often connect to real scenarios like pricing, distance, or growth.
Systems of Two Linear Equations in Two Variables
Some SAT algebra questions ask you to find values that satisfy two equations at the same time. You may solve systems using substitution, elimination, or graph interpretation. A system may also be used to model a situation with two changing quantities. Recognizing whether a system has one solution, no solution, or infinitely many solutions is an important skill for SAT algebra practice.
Linear Inequalities in One or Two Variables
These questions involve identifying solution sets, graphing inequalities, or interpreting ranges of values. You may compare expressions or determine which values fit a condition. Linear inequalities on the SAT can include one variable or two, and many items connect to real-world modeling. Practicing SAT algebra questions with inequality constraints helps you analyze boundaries and translate them into mathematical relationships.
If you want a structured way to review these topics, our SAT study guide offers clear explanations and comprehensive coverage of algebra concepts so you can build a strong foundation before practicing full questions.
SAT Algebra Practice Questions With Answer-Explanations
Linear Equations in One Variable
Question
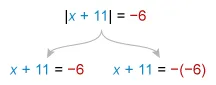
|x + 11| = −6
How many solutions does the given equation have?
| A. Zero | |
| B. Exactly one | |
| C. Exactly Two | |
| D. More than two |
The absolute value of a number is its distance from 0 and must be positive or 0.
Explanation
The absolute value of a number is its distance from 0 and must be positive or 0. It is possible for an absolute value equation to have 0, 1, 2, or an infinite number of solutions.
Notice in the given equation |x + 11| = −6 that the left side is an absolute value and the right side is a negative number. An absolute value cannot be equal to a negative number, so the equation must have zero solutions.
Note: It is possible to solve the equation |x + 11| = −6 to see that it has zero solutions (see alternate method).
(Choices B and C) These choices may result from disregarding the fact that an absolute value equation might have extraneous solutions.
(Choice D) More than two solutions to an absolute value equation when one of the two linear equations (see alternate method) results in an infinite number of solutions.
Things to remember:
- The absolute value of a number must be positive or 0.
- It is possible for an absolute value equation to have 0, 1, 2, or an infinite number of solutions.
Alternate Method :
It is also possible to solve the given equation. The question asks for the number of solutions, so it is necessary to plug the solutions back in to check if they are extraneous (not valid).
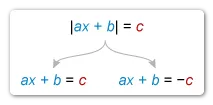
To find the solutions to an absolute value equation of the form |ax + b| = c , first find the solutions to the two equations ax + b = c and ax + b = −c.
Rewrite the given equation |x + 11| = −6 as two equations.
The two equations are x + 11 = −6 and x + 11 = 6. Solve each for x.
| x + 11 = −6 | x + 11 = 6 | |
| x = −17 | Subtract 11 from both sides | x = −5 |
Now check if −17 and −5 are valid solutions to the given absolute value equation. Plug each solution into |x + 11| = −6 and simplify.
| |x + 11| = −6 | Given equation | |x + 11| = −6 |
| |−17 + 11| = −6 | Plug in values of x | |−5 + 11| = −6 |
| |−6| = −6 | Simplify inside absolute value | |6| = −6 |
| 6 = −6 | Apply absolute value | 6 = −6 |
Both x = −17 and x = −5 result in the false statement 6 = −6, so both solutions are extraneous.
Therefore, the given equation has zero solutions.
Things to remember:
-
To find the solutions to an absolute value equation of the form |ax + b| = c, first find the solutions to the two equations ax + b = c and ax + b = −c.
-
It may be necessary to plug solutions back into the given absolute value equation to check if they are valid or extraneous.
Linear Equations in Two Variable
Question
y = kx
The relationship between x and y is given by the equation above, where k is a constant. If y = 42 when x = 6, what is the value of y when x = 14 ?
Use the given pair of corresponding values (y = 42 when x = 6) to find the value of the constant k.
Explanation
Correct Answer: 98
To find the value of y when x = 14, first use the given pair of corresponding values (y = 42 when x = 6) to find the value of the constant k. Plug y = 42 and x = 6 into the given equation y = kx and solve for k.
| y = kx | Given equation |
| 42 = k(6) | Plug in y = 42 and x = 6 |
| 7 = k | Divide both sides by 6 to solve for k |
It is given that k is a constant, so its value does not change. Plug in k = 7 for k in y = kx.
| y = kx | Given equation |
| y = 7x | Plug in k = 7 |
Therefore, the relationship between x and y is modeled by the equation y = 7x. To find the value of y when x = 14, plug in x = 14 and solve for y.
| y = 7x | |
| y = 7(14) | Plug in x = 14 |
| y = 98 | Multiply |
When x = 14, the value of y is 98.
Things to remember:
- To find the value of a constant k in the equation y = kx, plug in a pair of corresponding values for x and y.
- If y = b when x = a, then a and b are corresponding values and form the (x, y) pair (a, b).
Linear Functions
Question
The equation d = 830 − 0.734T models the density d, in kilograms per cubic meter, of fuel oil at a temperature of T degrees Celsius (°C) above room temperature. What is the increase in temperature, in degrees Celsius, that is necessary to decrease the density by 1 kilogram per cubic meter?
| A. | |
| B. | |
| C. 830 | |
| D. 0.734 |
The rate of change of the given equation is the change in density per degree Celsius. Use this rate of change to determine the change in temperature that corresponds to a decrease in density of 1 kilogram per cubic meter.
Explanation
The slope-intercept form of a linear equation is y = mx + b, where m is the rate of change (slope) and b is the initial value (y-intercept).
The rate of change describes how one quantity changes with respect to another, while the initial value is a fixed amount of one of those quantities. The rate of change does not depend on the initial value.
The rate of change m of a quantity y per quantity x is equal to the change in y divided by the change in x.
The given equation d = 830 − 0.734T represents a linear relationship. Use the rate of change to find the increase in temperature that results in a decrease in density of 1 kilogram per cubic meter (kg/m3).
Compare the given equation to y = mx + b to identify the rate of change m. First rearrange d = 830 − 0.734T to match this form, and then identify the rate of change. Notice that d corresponds to y and T corresponds to x.
| y = mx + b | ||
| d = −0.734T + 830 | ⇒ | m = −0.734 |
The rate of change m = −0.734 is the change in density d per degree T and is equal to the change in density divided by the change in temperature.
Note: The rate of change is negative, so a change in temperature causes the opposite change in fuel oil density. When the temperature increases (positive change), density decreases (negative change).
The question asks for the increase (or change) in temperature that results in a decrease in density of 1 kilogram per cubic meter, so the change in density is −1 kg/m3. Let the change in temperature be x.
Plug in the rate of change (−0.734) and the change in density (−1), and then solve for x.
| Plug in values | |
| Multiply both sides by x | |
| Divide both sides by −0.734 |
Notice that this value matches an answer choice, so do not simplify this result. An increase in temperature T of degree Celsius will decrease the density of the fuel oil d by 1 kilogram per cubic meter.
Note: The rate of change of a linear equation is the slope of its graph, so it is also possible to analyze the slope of the graph of d = 830 − 0.734T to write the equation
(Choices A and C) 1830 and 830may result from mistaking the initial value (y-intercept) of the equation for the rate of change (slope). However, the initial value of a linear equation does not affect the amount by which the density changes per degree.
(Choice D) 0.734 may result from the misconception that the question asks for the decrease in density based on an increase in temperature of 1 degree, but the question asks for the increase in temperature that results in a decrease in density of 1 kilogram per cubic meter.
Things to remember:
-
The slope-intercept form of a linear equation is y = mx + b, where m is the slope (or rate of change) and b is the y-intercept (or initial value).
-
The rate of change of a quantity y per quantity x is equal to the change in y divided by the change in x.
Systems of Two Linear Equations in Two Variables
Question
The solution to the given system of equations is (x, y). What is the value of 4x+5y ?
It is possible to solve directly for the desired expression from the given system of equations.
Explanation
Correct Answer: 6
If a question asks for the value of an expression instead of a single variable (ex. x or y) based on a system of two equations, it may be possible to solve for the expression directly. The question asks for the value of 4x + 5y.
In the given system of equations, notice that the x-terms are opposite and the y-terms are the same. Add the equations to get an equation containing only y, and subtract the equations to get an equation containing only x.
Notice that the resulting equations contain the desired y-term and the desired x-term. Divide to isolate 5y and 4x in the equations.
| 6(5y) = 36 | Resulting equations | 12(4x) = 0 |
| 5y = 6 | Divide to isolate 5y and 4x | 4x = 0 |
Plug 4x = 0 and 5y = 6 into the desired expression 4x + 5y and simplify.
| 4x + 5y | Desired expression |
| 0 + 6 | Plug in 4x = 0 and 5y = 6 |
| 6 | Add |
The value of 4x + 5y is 6.
Things to remember:
If a question asks for the value of an expression instead of a single variable based on a system of two equations, check if it is possible to solve for the expression directly by adding or subtracting the equations.
Alternate Method :
Although less efficient, it is possible to use the elimination method to first solve for the individual values of x and y and then find the desired expression 4x + 5y.
The x-terms are opposite, so add the two equations to eliminate the x-term and then solve for 5y.
The value of y is , so plug into either equation to get an equation in terms of only x. Then solve for x.
| 6(4x) + 3(5y) = 18 | First equation |
| Plug in y = 6/5 | |
| 24x + 18 = 18 | Multiply on the left |
| 24x = 0 | Subtract 18 from both sides |
| x = 0 | Divide by 24 on both sides |
The value of x is 0 and the value of y is 65, so plug these values into the desired expression 4x + 5y.
| Desired expression | |
| Plug in x = 0 and y = 6/5 | |
| Simplify |
Things to remember:
To solve a system of equations with the elimination method, rewrite the system as a single equation in one variable:
- Rewrite the system so that a pair of variable terms is the same or opposite if they are not already.
- Add or subtract the equations to eliminate that variable.
Linear Inequalities in One or Two Variables
Question
Which of the following number lines represents the set of all solutions to 2x − 1 > 5 ?
| A.
|
|
| B.
|
|
| C.
|
|
| D.
|
First solve the given inequality for x, and then match the solution to the correct number line.
Explanation
To find the number line that represents the set of solutions to the given inequality, first solve the inequality for x.
To solve 2x − 1 > 5, isolate x so that it is by itself on one side of the inequality.
| 2x - 1 > 5 Given inequality |
| 2x > 6 Add 1 to both sides |
| x > 3 Divide by 2 on both sides |
The solution to the given inequality is x > 3.
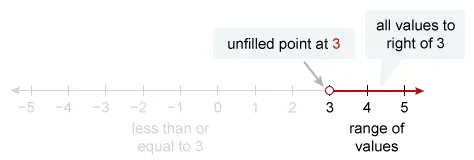
Therefore, the solution set includes all numbers greater than (but not equal to) 3. The number line that represents these solutions has an unfilled point at 3 and a bold line for all values to the right of 3.
The number line in Choice A represents the set of all solutions to 2x − 1 > 5.
(Choice B)This number line represents x < −3 and may result from a sign error when isolating x and mistakenly flipping the inequality sign. It is necessary to flip the inequality sign only when multiplying or dividing by a negative number.
(Choice C)This number line represents x > 2 and may result from a calculation error when isolating x.
(Choice D)This number line represents x < −2 and may result from the combination of errors described in Choices B and C.
Things to remember:
- To find solutions of an inequality, isolate the unknown so that it is by itself on one side of the inequality.
- On a number line:
- A filled point represents a specific value included in the data set.
- An unfilled point represents a specific value not included in the data set.
- A bold line represents a range of values.
How to Break Down SAT Algebra Problems Clearly
Understanding how to approach SAT algebra questions step by step can make even complex problems feel manageable. Instead of jumping straight to solving, it helps to read carefully, define variables, and translate information into equations. Whether you are working on linear equations, systems, or SAT algebra practice questions involving functions, a structured method improves accuracy.
Identify the Structure Before Solving
Understand what type of SAT algebra problem you are facing before doing any calculations. This helps you decide the fastest and most accurate solving method.
Tips:
- Check whether the question includes one variable, two variables, or a function rule.
- Look at the format for clues such as standard form, slope-intercept form, or factored form.
- Decide whether the problem requires solving, interpreting, or comparing expressions.
- Eliminate unnecessary information that does not affect the equation.
Translate Words → Equation → Expression
Many SAT algebra practice questions begin as real-world descriptions, so converting text to math is a key skill. Treat the scenario as a puzzle where each phrase corresponds to a mathematical action.
Tips:
- Identify what the question is asking you to find and assign variables.
- Replace key phrases like "total", "difference", "increased by", or "per" with operations.
- Keep expressions clear and organized before solving or simplifying.
- Read the final result again to confirm it fits the original context.
Look for Relationships (Slope, Intercepts, Changes)
When working with graphs or functions, focus on how quantities relate rather than looking only for a numerical result. Recognizing patterns speeds up solving and improves accuracy.
Tips:
- Identify the slope as the rate of change and the intercept as the starting point.
- Compare how changes in coefficients affect steepness, direction, or graph shifts.
- Check whether the problem is asking for interpretation rather than calculation.
- Use tables or patterns to verify relationships when multiple forms are presented.
When to Use a Quick Sketch for Functions
A fast sketch can make a complex algebra problem easier to visualize. You do not need a perfect graph, only something clear enough to help decision-making.
Tips:
- Sketch when the question involves comparing forms, direction of change, or intercepts.
- Draw only the essential points, such as slope and intercept, not every plotted value.
- Use the sketch to eliminate obviously incorrect answer choices.
- Keep the drawing simple to save time during the SAT.
Hard Algebra Problems: How the SAT Tries to Trick You
Some SAT algebra problems are written to challenge reasoning rather than straightforward memorization. You may see unusual phrasing, unnecessary numbers, or answer choices crafted to match common errors. These questions are meant to test precision and logical thinking. With steady SAT algebra practice, these patterns become easier to identify and manage.
Trap 1: Extra or Irrelevant Information
Some questions contain details that look important but do not affect the solution. The SAT exam includes this to see if you can filter what matters. Focusing only on values that contribute to an equation or function prevents confusion and saves time.
Trap 2: Answer Choices Based on Common Errors
Distractor choices often reflect mistakes such as sign errors, skipped steps, or incorrect simplification. Slowing down when distributing, combining terms, or dealing with negatives helps avoid falling for these traps.
Trap 3: Complicated or Unexpected Expression Forms
A linear or quadratic expression may appear in factored form, vertex form, or standard form simply to test whether you can interpret structure. Rewriting the expression into a more familiar format can make the problem easier to analyze and solve.
Trap 4: Misleading or Irregular Graph Details
Graphs sometimes use unusual scales, unlabeled axes, or intervals that do not increase consistently. Checking axes carefully before interpreting slope or intercepts prevents incorrect assumptions and improves accuracy.
Trap 5: Hidden Relationships in Word Problems
Some SAT algebra questions use language that implies mathematical meaning instead of stating it directly. Words like “remaining,” “each,” or “at least” hint at operations or inequality structures. Translating slowly and confirming the meaning ensures the equation models the scenario correctly.
Using exam-like resources, such as an SAT Practice Question Bank, can strengthen these skills, making real test algebra questions easier to tackle on test day.
Strategies to Solve SAT Algebra Questions Faster
Time management matters on the SAT, and knowing efficient approaches can help you move through challenging problems with confidence. Whether you are solving SAT algebra practice questions or working through official test items, the goal is to reduce unnecessary steps and avoid guesswork. With the right strategies, you can approach SAT algebra problems systematically and improve both speed and accuracy.
- Start With the Simplest Form: If an equation or function looks complicated, try simplifying before solving. Factoring, combining like terms, or converting to slope-intercept form often reveals the solution path quickly. A cleaner format makes it easier to plug in values or interpret the structure.
- Use the Answer Choices Strategically: Some algebra SAT math questions are faster when you test answer choices rather than solve traditionally. Substituting a value directly into the equation can help confirm whether a choice works. This approach is especially useful for inequalities, function tables, or systems.
- Know When to Estimate Instead of Solve Exactly: If multiple answers fall far apart numerically, estimation can get you to the correct choice faster. Focus on identifying reasonable ranges or spotting whether a value should be positive, negative, increasing, or decreasing.
- Recognize Patterns and Repeated Formats: SAT algebra questions often reuse the same structures, such as linear modeling, slope interpretation, or solving a basic system. Identifying familiar patterns reduces hesitation and helps you choose the correct method without overthinking.
- Skip and Return When Needed: If a problem feels unusually long or unclear, move past it and return later. Timing is important, and spending too long on a single question can reduce opportunities to gain easier points elsewhere in the section.
If you prefer learning through step-by-step instruction, our SAT prep course includes video lessons, guided examples, and strategy tips that walk you through every SAT algebra question type you will see on test day.
SAT Algebra: Frequently Asked Questions
How many algebra questions appear on the SAT?
Algebra makes up a large portion of the SAT Math section, so you can expect around one-third of the questions to be related to SAT algebra concepts. These items include linear equations, inequalities, systems, and function interpretation. Because of this consistent weighting, practicing SAT algebra questions can significantly boost your overall score. Strong skills in this area often make the test feel more predictable.
Do I need to memorize algebra formulas?
Most algebra formulas used on the SAT are based on concepts you already practiced in school. You do not need to memorize a long list, but you should be comfortable with slope, function notation, systems, and basic equation solving. The more familiar you are with these ideas, the faster you can solve SAT algebra practice questions. Knowing when and how to apply a formula matters more than simple memorization.
Is there Algebra 2 on the SAT?
Some students wonder whether Algebra 2 is on the SAT, and the answer is partly yes. While most questions come from Algebra 1, certain topics, such as exponential relationships and more complex functions, connect to Algebra 2 skills. These questions are still approachable with strong foundational knowledge. Consistent SAT algebra practice helps you work through both levels with confidence.
Are SAT algebra questions hard?
Difficulty varies, but many SAT algebra questions are designed to test reasoning rather than advanced math. The content itself is familiar, yet wording, structure, and answer choices can make a problem feel challenging. With practice, the patterns become easier to recognize. Building problem-solving strategies can make these questions feel much more manageable.
What algebra topics appear most often?
Linear equations, inequalities, systems, and function interpretation appear frequently, along with occasional exponential questions. These form the core of SAT algebra practice problems and consistently show up throughout the test. Because these topics repeat, building fluency with them provides a strong advantage. Recognizing formats and relationships can speed up solving significantly.
Do I get a formula sheet for algebra on the SAT?
The SAT provides a formula sheet, but it focuses mostly on geometry rather than algebra. This means you should already be familiar with common algebra rules before test day. Practicing SAT algebra practice questions helps reinforce these skills until they feel automatic. By the time you take the test, most algebra steps should feel natural.