AP® Calculus BC Unit 9 Review and Practice Test
Master AP® Calculus BC Unit 9 with UWorld’s in-depth review. Learn how to represent motion, area, and rate of change across multiple coordinate systems. With expert video lessons, clear study guides, and challenging practice tests, UWorld helps you connect geometry, calculus, and motion into one complete understanding. Strengthen your visualization and problem-solving skills to boost your performance on every AP Calc BC Unit 9 question.
Gain Clarity and Exam Confidence with UWorld’s AP Calculus Unit 9 Review
Unit 9 introduces new mathematical perspectives, including parametric, polar, and vector representations of motion and change. UWorld’s AP Calculus BC Unit 9 review breaks these topics into simple, visual explanations that connect directly to the AP Exam format. Every question and explanation helps you understand not just the computation but the geometric meaning behind it, which is essential for both multiple-choice and FRQs.
Engage with Polar and Parametric Functions
See motion come alive through UWorld’s detailed AP Calculus BC polar review and parametric lessons. Each video simplifies complex geometric behavior into step-by-step visuals, showing how derivatives define speed, direction, and curvature.
Make Learning Easy with Interactive Study Guides
UWorld’s interactive study guides make abstract coordinate systems feel intuitive. Each AP Calculus BC polar and parametric review page pairs visual graphs with the calculus that defines them. Instead of memorizing formulas, you’ll understand their origins and applications, vital for FRQs that demand explanation as much as computation.
Challenge Yourself with These AP Calculus BC Unit 9 Practice Test Questions
Question
If h is a vector-valued function defined by , then hʹʹ(t) =
| A. | |
| B. | |
| C. | |
| D. |
The second derivative of the vector-valued function h is the vector containing the second derivatives of each component of h.
Explanation
The second derivative of the vector-valued function h is the vector containing the second derivatives of each component of h.
To find the components of hʹʹ, differentiate each component of the given vector-valued function twice.
Use the chain rule to differentiate the composite function x(t) = e4t, and use the power rule to differentiate y(t) = t4 to find the components of hʹ.
The components of hʹ are xʹ(t) = 4e4t and yʹ(t) = 4t3. Now use the chain rule to differentiate xʹ(t), and use the power rule to differentiate yʹ(t) to find the components of hʹʹ.
Therefore, the second derivative of the given vector-valued function is .
(Choice A) may result from incorrectly applying the power rule to differentiate yʹ(t) = 4t3.
(Choice C) is the first derivative of h, but the question asks for the second derivative.
(Choice D) may result from not applying the chain rule when differentiating xʹ(t) = 4e4t.
Things to remember:
The derivative of a vector-valued function
is the vector of the derivatives of each component of f.
Question
If and , for t > 0, what is in terms of t ?
| A. | |
| B. | |
| C. | |
| D. |
To find the second derivative of a parametrically defined function in terms of t, first find in terms of t.
Explanation
The notation represents the second derivative of y with respect to x. To find the second derivative of a parametrically defined function in terms of t, first divide by to find in terms of t.
Then differentiate with respect to t and divide the result by :
Differentiate the equations for x and y independently with respect to t to find and . First use a negative exponent to rewrite the y equation as t−1.
| Given equations for x(t) and y(t) | ||
| Apply power rule to differentiate |
Now divide the expression for by the expression for to find .
| Parametric first derivative | |
| Substitute and | |
| Multiply by the reciprocal and simplify |
Differentiate with respect to t and then divide the result by . Use a negative exponent to rewrite the first derivative as and then differentiate with respect to t.
| First derivative | |
| Differentiate and simplify |
Now plug in and into the equation for and simplify.
| Parametric second derivative | |
| Substitute and | |
| Multiply by the reciprocal and simplify |
Therefore, .
(Choice B) may result from not dividing by .
(Choice C) is the first derivative of the parametric function , but the question asks for the second derivative .
(Choice D) is the result of mistakenly dividing by to determine .
Things to remember:
To find
in terms of t for a parametrically defined function, differentiate
with respect to t and then divide the result by
:
Question
A particle moves along the -plane with position given by the parametric equations x(t) = t2 – 7 and y(t) = 8 – 2t. In which direction is the particle moving as it passes through the point (−3, 4) ?
| A. Up and to the left | |
| B. Down and to the left | |
| C. Up and to the right | |
| D. Down and to the right |
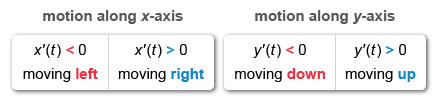
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).
Explanation
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).
Differentiate the given equations x(t) and y(t) with respect to to write equations for x'(t) and y'(t).
| Given equations for x and y | ||
| Differentiate |
Since y'(t) < 0 for all t, the particle is moving down for all t. It is possible to eliminate choices A and C.
To determine the horizontal direction of the particle as it passes through the point (−3, 4), it is first necessary to find the value of for which the position of the particle is (−3, 4). Substitute x(t) = −3 and y(t) = 4 and then solve each equation to find the value of that satisfies both equations.
Therefore, the particle passes through the point (−3, 4) when t = 2.
It was shown above that the particle is moving down for all t. Plug t = 2 into x'(t) to determine if the particle is moving to the left or to the right when it passes through the point (−3, 4).
| Equation for | |
| Plug in |
Since x'(2) > 0, the particle is moving to the right at time t = 2.
Therefore, when the particle passes through the point (−3, 4) it is moving down and to the right.
(Choice A) "Up and to the left" may be the result of mistakenly using the signs of y'(t) to determine the horizontal direction and x'(t) to determine the vertical direction.
(Choice B) "Down and to the left" may be the result of mistakenly plugging in the coordinates of the given point x = −3, y = 4 for the value of t in the equations for x'(t) and y'(t).
(Choice C) "Up and to the right" may be the result of an error when differentiating x'(t) .
Things to remember:
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).

Carry Unit 9 Practice Anywhere You Go
Keep your AP Calculus BC Unit 9 study routine flexible and effective. Whether you’re reviewing before class or solving vector motion problems on the go, the UWorld app keeps everything synced across devices. Study offline, track your progress, and access explanations at any time. Your full AP Calculus BC Unit 9 review experience fits wherever you are, so preparation never stops when you’re away from your desk!
Stand Out
with a Top Score on the AP Calculus BC Exam
Complete your comprehensive AP Calculus BC Unit 9 review to boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
Which major topics fall under “Parametric Equations, Polar Coordinates, and Vector-Valued Functions”?
AP Calculus BC Unit 9 focuses on extending calculus beyond standard Cartesian graphs. The unit explores how motion, area, and rate of change behave in parametric, polar, and vector forms. These ideas combine algebraic reasoning with geometric intuition, making them critical for problem-solving on both the MCQs and FRQs.
Core topics include:
- Finding derivatives of parametric functions and vector-valued functions
- Calculating the accumulation of change in length over an interval using a definite integral
- Determining the position of a particle moving in a plane
- Calculating velocity, speed, and acceleration of a particle moving along a curve
- Finding derivatives of functions written in polar coordinates
- Finding the area of regions bounded by polar curves
UWorld’s AP Calculus BC Unit 9 Review ties these ideas together with dynamic visuals and guided, step-by-step solutions. The platform doesn’t just show how to calculate derivatives, but shows why curves behave the way they do. By integrating geometric interpretation with calculus operations, UWorld helps students develop a conceptual fluency that turns complex multi-variable motion into manageable, logical reasoning, which the AP Exam rewards.
How should I prepare for an AP Calculus BC Unit 9 exam?
Success in AP Calculus BC Unit 9 requires comfort with visualizing motion and connecting calculus operations to geometry. Preparation should strike a balance between theory and timed problem-solving. The best approach is to build understanding, then train the application.
Follow this focused strategy:
- Start with visualization. Use UWorld’s videos to grasp how parametric and polar equations describe motion, slope, and area.
- Reinforce with guided practice. Work through the AP Calculus BC Unit 9 review study guides to summarize formulas, definitions, and key relationships.
- Test your timing. Attempt short quizzes using practice test sets under time constraints to simulate real exam pressure.
- Review thoroughly. Always read explanations, even for correct answers, to strengthen reasoning, not just accuracy.
This rotation of learn, apply, and reflect ensures retention and pattern recognition. Unit 9 questions test not only computation but also conceptual translation between coordinate systems. UWorld’s analytics show precisely where you slow down or misinterpret slope or area logic, helping you fix gaps early. By the time you reach the AP Exam, this steady exposure trains you to read multi-variable problems intuitively and answer with confidence.
How can I use UWorld to prepare for AP Classroom’s Progress Check MCQs and FRQs?
The College Board’s AP Classroom progress checks are designed to test your understanding of each unit’s core concepts, including AP Calculus BC Unit 9. These aren’t part of the official AP Exam but serve as valuable benchmarks. UWorld’s structure mirrors its intent, working to strengthen conceptual accuracy and reasoning clarity through guided practice.
Each topic in UWorld’s AP Calculus BC Unit 9 review includes Check-for-Understanding and FRQ-style questions that assess knowledge exactly like progress checks do. When you answer, you’re not just confirming facts but building analytical depth. The explanations detail why certain responses work and how errors emerge, mimicking the reflective process teachers expect during progress check reviews.
For the best results:
- Review one UWorld topic (parametric, polar, or vector) before attempting your classroom progress check.
- Revisit UWorld’s FRQ examples to practice structured justification, which directly improves written performance.
- Use analytics to pinpoint recurring mistakes before your teacher assigns similar problems.
This method aligns classroom readiness with AP Exam preparation. Students who pair UWorld practice with official progress checks report greater confidence, faster recognition of question patterns, and improved long-term retention, proof that learning through reasoning beats memorization every time.
How much time should I spend reviewing Unit 9 before the exam?
The ideal AP Calculus BC Unit 9 review plan spans 10-14 focused hours over 2-3 weeks before the AP Exam. This unit demands both computational fluency and spatial reasoning, so review time should combine conceptual study and visual practice.
Here’s a breakdown for maximum effectiveness:
- 3-4 hours: Review fundamentals of parametric differentiation and vector motion using UWorld’s videos.
- 4-5 hours: Practice interpreting polar graphs and solving arc length or area problems using AP Calculus BC Unit 9 practice test sets.
- 3-4 hours: Integrate all forms – parametric, polar, and vector – into timed mixed quizzes to simulate exam pacing.
- Each UWorld session reinforces learning through explanation, not repetition. Reviewing rationales after every question helps link derivative rules, trigonometric functions, and curve geometry in a seamless manner.
Spread the hours across short, consistent sessions rather than long, cramming blocks. Students who review this way not only improve memory retention but also develop a stronger sense of pattern recognition, making even complex motion questions feel predictable on test day.
How does UWorld help strengthen my geometric visualization skills for Unit 9?
Understanding geometry is central to Unit 9 AP Calculus BC. Many questions require you to visualize curves, directions, and motion across coordinate systems. UWorld’s visual-first approach makes abstract relationships tangible, helping you grasp how calculus explains motion rather than just computing results.
Every AP Calculus BC Unit 9 review question includes diagrams illustrating slope, direction, and curvature. When solving polar problems, you see how radius and angle interact to shape the curve. For parametric and vector problems, UWorld animates how velocity and acceleration change along a path.
This visual integration is key for retention. When students see how each variable transforms a curve, conceptual recall becomes effortless during exams. Over time, these graphical cues replace rote memorization with understanding as you begin to “see” solutions before solving them.
Regular UWorld practice builds what educators call spatial calculus fluency, the ability to interpret and manipulate equations as geometric behaviors. That mental shift allows you to approach any Unit 9 problem, no matter how complex, with calm precision and visual logic.
Are any free resources available for AP Calculus BC Unit 9?
Yes. There are several free resources available for AP Calculus BC Unit 9, but not all provide the structure and clarity needed for exam readiness. The College Board offers course outlines, sample problems, and videos that introduce parametric, polar, and vector topics. These materials explain the basics but often lack clear guidance or effective problem-solving strategies.
UWorld’s free trial is one of the most valuable resources for this unit. It includes video lessons, sample AP Calc BC Unit 9 review questions, and visual explanations that align closely with the AP Exam’s conceptual depth. Every question in the free trial is presented in the same analytical style found on the real exam, helping you connect geometric intuition to calculus computation.
To get the most from free materials, follow a structured plan:
- Spend the first few days revisiting basic formulas for slope, area, and motion.
- Practice two to three UWorld questions per day, reading each explanation carefully.
- Use the interactive graphs and notes to reinforce visual understanding.
Even UWorld’s free trial access teaches problem-solving rather than mechanical application. Combined with official outlines, this hybrid approach provides a free yet effective starting point for mastering Unit 9 AP Calc BC without sacrificing conceptual depth.
What types of questions are on the AP Calculus BC Unit 9 test?
The AP Calculus BC Unit 9 test evaluates how well students can apply calculus to non-Cartesian systems. Instead of traditional derivatives or integrals, the questions focus on interpretation, translation, and problem setup. You must connect geometric meaning with algebraic computation.
Typical question categories include:
- Parametric Equations: Find tangent lines, arc lengths, or speed using x(t) and y(t).
- Polar Coordinates: Determine slopes, enclosed areas, or curve intersections using r(θ).
- Vector-Valued Functions: Calculate velocity, acceleration, and total distance using vector relationships.
FRQs often combine multiple concepts, requiring written justification and interpretation of motion. MCQs, on the other hand, test speed, recognizing formulas, relationships, and geometric cues quickly. UWorld’s AP Calculus BC Unit 9 Review ensures familiarity with both formats. Every problem mirrors AP style, presenting realistic curve visuals and data-driven motion contexts. The explanations then translate each question into plain logic, explaining why the answer works and what it means.
After repeated UWorld practice, students report that polar and parametric setups feel intuitive, not intimidating. Recognizing question types becomes instinctive, which translates directly into higher accuracy and faster responses during the actual exam.
How does UWorld keep students motivated while preparing for AP Calculus BC Unit 9?
Studying AP Calculus BC Unit 9 can feel overwhelming because it merges algebraic manipulation with geometric reasoning. UWorld maintains high motivation by transforming complex study sessions into guided, measurable progress. Each question you solve contributes to visible improvement and encouragement, which is critical during intensive AP prep.
Motivation in UWorld comes from feedback. After every AP Calculus BC Unit 9 practice test, you receive analytics on accuracy, pacing, and mastery by topic. Seeing your weak points evolve into strengths transforms effort into confidence.
In addition, UWorld’s features keep studying engaging:
- Smart Flashcards: Let you turn difficult Unit 9 problems into personalized micro-quizzes.
- Mobile Sync: Enables quick practice sessions anywhere, anytime.
- Stepwise Explanations: Give immediate insight into every correct and incorrect option, ensuring every session teaches something new.
This steady cycle of progress tracking and active learning reduces burnout. Instead of passive reading, you’re continuously learning through small, rewarding wins. By the time the AP Exam arrives, confidence replaces anxiety, and you’ll know your preparation wasn’t random but reinforced through data, reasoning, and repetition.
How can I improve my score on the MCQs and FRQs for Unit 9?
To raise your score on AP Calc BC Unit 9 MCQs and FRQs, you must combine precise calculation with conceptual fluency. The top-performing students don’t just memorize formulas but understand what each represents geometrically.
Focus on these targeted improvements:
- For MCQs: Practice recognition. Many questions rely on identifying the correct derivative or setup quickly. UWorld’s ap calculus bc unit 9 review trains you to see patterns, such as the link between parametric velocity and slope or the structure of polar area integrals.
- For FRQs: Prioritize explanation. Write complete sentences connecting calculus to motion or area. UWorld’s modeled FRQ solutions demonstrate an ideal structure and justify reasoning in concise yet clear steps.
Reviewing both formats regularly helps align your thinking with the expectations of AP graders. UWorld’s feedback analytics highlight time usage, accuracy, and conceptual gaps, making your revision more data-driven and intentional.
Over time, this feedback loop shifts your performance from reactive to strategic. You’ll approach Unit 9 problems with clarity, seeing not just how to solve but why the method works, which is the mindset behind every consistent 5.
What is the "Parametric Equations, Polar Coordinates, and Vector-Valued Functions" unit's weight on the AP Calculus BC exam?
The AP Calculus BC Unit 9 topics collectively account for around 11-12% of the total AP Calculus BC Exam. This includes questions that test geometric understanding, motion interpretation, and integration in alternative coordinate systems. While not the largest content area, Unit 9 is considered one of the most conceptually demanding sections, often determining top-tier scores.
You can expect at least one FRQ or several MCQs covering these representations. AP Exam questions frequently blend these topics with earlier calculus principles, such as differentiation, applications of the chain rule, and integration techniques. This interconnected nature makes Unit 9 a synthesis unit, requiring you to apply knowledge flexibly rather than in isolation.
UWorld’s AP Calculus BC Unit 9 Review prepares you to handle this integration confidently. Each practice question demonstrates how polar slopes, parametric derivatives, and vector motion link back to earlier units. The detailed solutions not only show the calculation but also interpret how a curve’s geometry reveals its physical meaning.
Students who invest focused review time here typically see better results across multiple exam sections, since Unit 9 reinforces the reasoning skills central to calculus itself: understanding relationships between variables, interpreting change, and explaining outcomes logically.
What’s the best way to organize my formula sheet for integrals?
Even though the AP Exam provides a formula sheet, organizing your own version while reviewing Unit 9 AP Calculus BC can significantly improve memory recall. The goal isn’t just listing equations, but categorizing relationships logically so they become second nature during problem solving.
Structure your sheet like this:
- By Representation: Separate formulas for Cartesian, parametric, and polar coordinates.
- For Parametric Equations: Include arc length formulas with labeled examples.
- For Polar Equations: Note slope and area formulas
- For Vector Functions: Add magnitude, velocity, acceleration, and motion relationships.
- Connections: Add short notes that link each representation back to standard differentiation and integration concepts.
Reviewing your sheet regularly helps train your pattern recognition. When you later attempt UWorld’s AP Calc BC Unit 9 practice problems, you’ll notice how often these forms repeat across contexts.
This organization helps more than just memory, as it strengthens problem-solving intuition. Instead of searching for formulas, you’ll instantly identify which relationships apply, saving valuable exam time. The best formula sheet isn’t decorative, but a map of understanding.
Where can I find a good study guide for AP Calculus BC Unit 9?
A great AP Calculus BC Unit 9 study guide should go beyond definitions and formulas, and help you visualize, interpret, and apply calculus to motion and geometry. Unit 9 combines analytical thinking with spatial awareness, so the best resources seamlessly blend explanation and illustration.
UWorld’s interactive study guide for AP Calc BC Unit 9 Review does precisely that. It organizes topics by representation and uses color-coded visuals to demonstrate how calculus describes motion across these systems. For example, you’ll see slope fields translated into parametric velocity components, or polar equations converted into area integrals with annotated diagrams.
Each concept includes step-by-step walkthroughs of problems, followed by brief takeaways that summarize the logic. The guide also flags notes that point out common traps, like sign errors when interpreting slope direction or mixing up θ and t in derivatives.
When paired with UWorld’s practice tests, this structure allows students to shift from memorization to reasoning. Every formula gains purpose. By test day, you’re not recalling symbols, but you’re seeing relationships unfold. That’s the difference between a generic study guide and one built for genuine AP Exam performance.
What are the most common mistakes students make on Unit 9 questions?
Many students lose points in Unit 9 AP Calc BC, not because of complex math, but due to conceptual misunderstandings. This unit requires translating calculus across multiple representations, such as Cartesian, parametric, polar, and vector, and even strong students may misalign variables or misinterpret geometry.
Here are the most frequent errors:
- Mixing parameters: Confusing θ (polar) with t (parametric), leading to incorrect derivatives or limits.
- Ignoring geometric meaning: Treating formulas mechanically instead of visualizing what area or slope represents.
- Sign confusion: Forgetting direction in motion problems or misapplying negative radii in polar coordinates.
- Incomplete FRQ explanations: Providing only equations instead of a written justification about motion or curve behavior.
UWorld’s AP Calculus BC Unit 9 Review targets these mistakes directly. Each problem highlights not just how to compute but why the logic works. The explanations include visual diagrams showing curve direction, radius change, and slope movement, helping you avoid mechanical errors.
By studying these reasoning cues, you’ll build the confidence to interpret graphs intuitively, spot subtle sign shifts, and write precise justifications, the hallmarks of a 5-level AP performance.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Differential Equations
Applications of Integration
Infinite Sequences and Series