Bundle 3+ College Prep products for 20% off

AP® Calculus BC Unit 8 Review and Practice Test

Applications of Integration

AP® Calculus BC Unit 8 focuses on using integrals to solve real-world problems involving area, volume, and motion. Review key concepts and practice exam-style questions with detailed answer explanations to boost your AP Calc BC exam score.

AP Calculus BC prep course suite by UWorld

Excel in AP Calculus BC Unit 8 with Smart Review Tools

Tackle tough integration problems with ease. Our AP Calc BC Unit 8 review simplifies advanced concepts, connects them to real-world applications, and helps you prepare confidently for test day.

Watch

Engaging Video Lessons

Learn AP Calculus BC Unit 8 concepts through engaging video lessons that break down applications of integrals into simple, visual explanations. Understand how to calculate areas, volumes, and accumulated change step-by-step. Each video connects theory to real AP Calc BC exam questions, helping you grasp every topic with confidence.

Preview Video Lesson
Buy Now
UWorld’s AP Calc BC Video Lessons
UWorld’s AP Calculus BC Study Guide Prep book
Read

Interactive Study Guides

Explore AP Calculus BC Unit 8 with interactive study guides that make complex integration concepts easier to understand. Each guide covers topics like areas between curves, volumes, and motion problems in clear detail. Review formulas, examples, and visuals designed to help you retain key ideas and perform better on your AP Calc BC exam.

Preview Book
Buy Now
Practice

Try These AP Calculus BC Unit 8 Practice Test Questions

Test your understanding of AP Calculus BC Unit 8 with realistic practice questions on applications of integrals. Work through problems involving area, volume, and accumulation to strengthen your problem-solving skills. Each AP Calc BC Unit 8 practice test question is designed to match the style and difficulty of the real exam.
Try these sample practice questions with detailed answer explanations:
Applications of Integration Practice Tests

Question

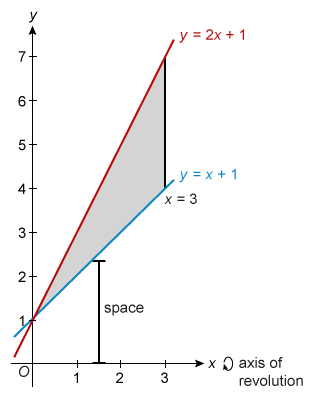
Which of the following is the volume of the solid generated by revolving the region bounded by the lines y = 2x + 1, y = x + 1, and x = 3 about the x-axis?

A. 9 π 2
B. 9 π
C. 27 π
D. 36 π

Explanation

To determine whether to use the disc or washer method, graph the given lines to see if there is space between the region and the x-axis.

reflexes

There is space between the region and the axis of revolution, so it is necessary to use the washer method to find the volume.

The top function is y = 2x + 1 and the bottom function is y = x + 1, so R(x) = 2x + 1 and r(x) = x + 1.  The region spans the interval of x-values [0, 3], so the limits of integration are 0 and 3.  Substitute the function and limits into the integral for the washer method and evaluate.

π ∫ x 1 x 2 ( ( R (x) 2 - (r (x) ) 2 ) dx Washer method integral
π ∫ 0 3 ( ( 2 x + 1 ) 2 - ( x + 1 ) 2 ) dx Substitute functions and limits
π ∫ 0 3 ( 4 x 2 + 4 x + 1 - ( x 2 + 2 x + 1 ) ) dx Expand binomials
π ∫ 0 3 ( 3 x 2 + 2 x ) dx Combine like terms
π [ x 3 + x 2 ] 0 3 Integrate
π [ 3 3 + 3 2 - ( 0 3 + 0 2 ) ] Apply FTC
36 π Simplify

Therefore, the volume of the solid is 36 π

Question

Which of the following gives the area of the region R bounded by the graph of y = ln x + 1 and the lines y = 3, x = 1, and x = e ?

A. ∫ e 3 ln x dx
B. ∫ 1 3 (e - ln x) dx
C. ∫ 1 e (ln x - 2) dx
D. ∫ 1 e (2 - ln x) dx

Explanation

It is given that the region R is bounded by the vertical lines x = 1 and x = e, so the area integral spans the interval [1, e].  Eliminate Choices A and B.

Region R is the area between the functions y = ln x + 1 and y = 3 on the interval [1, e].  To determine which is the top function and which is the bottom function, plug the endpoints of the interval into y = ln x + 1 and compare the resulting values to y = 3.

y = ln x + 1 Given function y = ln x + 1
y = ln 1 + 1 Plug in given x-values y = ln e + 1
y = 0 + 1 Evaluate logarithms y = 1 + 1
y = 1 Add y = 2

The function y = ln x + 1 is an increasing function that is less than 3 for x = 1 and x = e.  Therefore, y = 3 must be the top function and y = ln x + 1 must be the bottom function.

Substitute the functions f(x) = 3 and g(x) = ln x + 1 and the endpoints a = 1 and b = e into the formula for the area between two curves to find the integral that gives the area of region R.

∫ a b f( (x) - g (x)) dx Area of region R
∫ 1 e (3 - (ln x + 1) dx Substitute functions and values
∫ 1 e (2 - ln x) dx Distribute −1 and combine constants

The integral that gives the area of region R is ∫ 1 e (2 - ln x) dx (graph).

Question

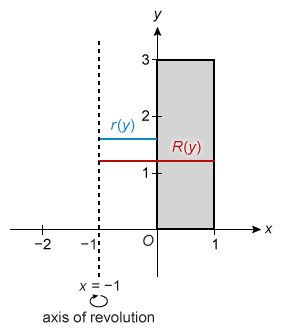
A program defines the dimensions of a certain coupling for a three-dimensional printer.  The coupling is defined as the rectangular area bound between x = 1, y = 3, and the x- and y-axes revolved around the vertical line x = −1.  What is the volume of the coupling?

A. 3𝜋
B. 9π
C. 12π
D. 15π

Explanation

It is given that the area revolves around a vertical line, so the volume integral is in terms of y.

Graph the given area and the axis of revolution to determine whether to use the disc or washer method.

There is space between the given area and the axis of revolution, so it is necessary to use the washer method.

The radii of each washer are R(y) = 1 − (−1) = 2 and r(y) = 0 − (−1) = 1, and the area spans the interval of y-values [0, 3].  Plug these values into the washer method volume integral and evaluate.

π ∫ y 1 y 2 ( ( R (y) ) 2 - ( r (y) ) 2 ) dy Washer method integral
π ∫ 0 3 ( ( 2 ) 2 - ( 1 ) 2 ) dy Plug in R(y) = 2, r(y) = 1, y1 = 0, and y2 = 3
π ∫ 0 3 3 dy Simplify integrand
π [ 3 y ] 0 3 Integrate
π [ 3 ( 3 ) - 3 ( 0 ) ] Apply FTC
9 π Simplify

Therefore, the volume of the coupling is 9 π

Buy Now
UWorld Dark Blue logo

Study Anywhere, Anytime

Study for AP Calculus BC Unit 8 wherever you are; watch short video lessons, solve practice problems, or review key formulas from your phone. With the UWorld app, your study materials are always within reach, making it easy to stay consistent and confident before exam day.

App Store
Google Play

Stand Out
with a Top Score on the AP Calculus BC Exam

Wrap up your AP Calculus BC Unit 8 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc BC Videos
  • Print & Digital Study Guide
  • 1800+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards & Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calculus BC Unit 8: Applications of Integration explores how definite integrals describe real-world change and accumulation. This unit applies mathematical concepts to motion, area, and volume, forming a key bridge between theory and application.

Here’s what you’ll study in this unit:

  • Average Value of a Function: Use definite integrals to find the mean output over an interval.
  • Modeling Particle Motion: Connect velocity and position using integrals.
  • Solving Accumulation Problems: Quantify change over time through integration.
  • Area Between Curves: Calculate the space enclosed by multiple functions.
  • Volume with Cross-Sections, Disc, and Washer Methods: Build 3D shapes from 2D regions.
  • Length of a Planar Curve: Use integrals to find the arc length of smooth curves.

With UWorld’s AP Calculus BC Unit 8 review and practice tests, you’ll see each of these applications in exam-style problems, helping you build strong problem-solving and conceptual understanding for test day.

Preparing for AP Calculus BC Unit 8 starts with a clear study structure. Begin by reading your notes or textbook to review the fundamentals of integration and its applications. Focus on topics like finding areas, volumes, and average values to refresh the key formulas and theorems.

Next, watch instructional videos to visualize concepts such as the disc and washer methods or motion modeling. Seeing problems worked out step-by-step helps you understand how integrals translate into geometric or physical meaning, making complex ideas easier to grasp.

Finally, practice with UWorld’s AP Calculus BC Unit 8 review. Solve realistic MCQs and FRQs that mirror the actual exam format, and use detailed explanations to learn from your mistakes. UWorld’s structured approach ensures you strengthen both accuracy and speed so you walk into test day confident and well-prepared.

For AP Calculus BC Unit 8, aim to spend one to two weeks focused solely on review before the exam. This unit, Applications of Integration, includes multiple essential concepts like areas, volumes, and motion, which often appear in both multiple-choice and free-response sections.

Divide your time strategically:

  • Days 1–3: Revisit lessons on definite integrals, disc and washer methods, and accumulation problems.
  • Days 4–6: Solve mixed practice questions and past FRQs related to integration applications.
  • Final days: Review key formulas, common errors, and speed drills to boost confidence.

If you’re unsure where to start, UWorld’s AP Calculus BC Unit 8 review provides a ready-made structure with topic-based questions and detailed feedback. It helps you use your time effectively, focusing on weak areas and reinforcing problem-solving accuracy before test day.

Yes, there are several excellent free options to help you prepare for AP Calculus BC Unit 8: Applications of Integration. You can start with Khan Academy, which offers comprehensive video lessons and practice problems covering areas, volumes, and motion using integrals.

The College Board website provides official practice materials, including free-response questions, multiple-choice examples, and detailed scoring guidelines that reflect real exam expectations. These resources help you understand the format and difficulty level of actual test questions.

For a more exam-focused experience, try the UWorld free trial for AP Calculus BC. It includes realistic Unit 8 practice questions, detailed explanations, and study tools that strengthen conceptual understanding and test-taking speed, all designed to help you feel confident on exam day.

The AP Calculus BC Unit 8 test includes a mix of multiple-choice questions (MCQs) and free-response questions (FRQs) that test your understanding of integration applications. You’ll encounter both calculator and non-calculator sections, assessing your ability to solve real-world problems using definite integrals.

Expect problems that involve:

  • Finding areas between curves and volumes using disc or washer methods.
  • Applying accumulation functions and the Fundamental Theorem of Calculus.
  • Solving motion problems involving velocity, position, and total distance traveled.
  • Determining average values or curve lengths using integrals.

For focused practice, use UWorld’s AP Calculus BC Unit 8 review and practice tests. Each question mirrors the exam’s style and rigor, providing detailed solutions that strengthen your reasoning and improve your performance under timed conditions.

Improving your FRQ performance for AP Calculus BC Unit 8 comes down to clarity, accuracy, and strategy. Start by reviewing past FRQs from College Board to understand common question types, such as volume calculations, average value problems, and motion-based integrals. Focus on showing every step, since partial credit is awarded for correct reasoning even if the final answer isn’t perfect.

Use a structured approach:

  • Clearly define variables and label units.
  • Write out integral expressions before solving.
  • Check if a graphing calculator is allowed and use it efficiently.
  • Always justify your answers with calculus-based reasoning, not guesses.

To strengthen your FRQ skills, practice with UWorld’s AP Calculus BC Unit 8 FRQs. Each problem includes step-by-step solutions and scoring insights that show how to earn every possible point, helping you turn your understanding into top-tier exam performance.

The “Applications of Integration” unit carries a significant portion of the AP Calculus BC exam, generally making up about 6–9% of the total score. Questions from this unit assess your ability to apply integrals to real-world contexts, including areas, volumes, and motion problems.

Expect both multiple-choice and free-response questions that require you to compute definite integrals, apply the disc or washer methods, and solve accumulation or particle motion problems. These questions test both conceptual understanding and problem-solving accuracy.

Using UWorld’s AP Calculus BC Unit 8 review and practice tests, you can tackle a variety of exam-style problems with detailed explanations. UWorld helps you identify weak areas, reinforce key concepts, and gain confidence in applying integration techniques effectively under timed conditions.

A well-organized formula sheet can save valuable time during the AP Calculus BC Unit 8 test. Group formulas by type, such as definite and indefinite integrals, disc and washer methods, accumulation functions, and motion equations. This makes it easier to quickly locate the right formula for each problem.

Include key integration techniques like substitution, integration by parts, and formulas for volumes and arc length. Highlight frequently used formulas or tricky integrals with color or symbols for quick reference. Keeping it concise helps prevent clutter and ensures you can quickly scan for the information you need.

UWorld’s AP Calculus BC Unit 8 review provides structured examples and practice problems that help you decide which formulas are essential. Using UWorld while building your formula sheet ensures that you focus on the concepts most likely to appear on the AP Calc BC exam and strengthens your problem-solving confidence.

UWorld’s AP Calculus BC Unit 8 review is one of the best ways to prepare for the Applications of Integration unit. It offers a structured approach with realistic practice questions, step-by-step solutions, and topic-specific explanations that strengthen your understanding of key concepts. UWorld also tracks your performance to highlight strengths and weaknesses, helping you focus on areas that need improvement. With its interactive tools, detailed feedback, and curated problem sets, UWorld makes it easier to grasp complex integration applications and build confidence for test day.

A great way to review AP Calculus BC Unit 8: Applications of Integration is to use a comprehensive study guide that covers all major topics, including areas between curves, volumes with disc and washer methods, accumulation functions, motion problems, and arc length. Focus on guides that break concepts into manageable sections with clear explanations and practice problems. For the most effective preparation, combine your coursework with UWorld’s AP Calculus BC Unit 8 review for realistic exam practice and targeted learning.

Students often lose points on AP Calculus BC Unit 8 questions due to misapplying integration techniques. Common errors include confusing disc and washer methods, forgetting to include constants when calculating indefinite integrals, or incorrectly setting up limits of integration for areas and volumes.

Other frequent mistakes involve misreading graphs in motion problems, neglecting the Fundamental Theorem of Calculus when computing accumulation functions, or making algebraic errors when simplifying integrals. Time management can also be an issue, causing rushed or incomplete solutions on longer free-response questions.

Practicing with UWorld’s AP Calculus BC Unit 8 review and practice tests can help you avoid these pitfalls. Its detailed step-by-step solutions, realistic exam-style questions, and performance tracking allow you to identify weak areas, correct common errors, and approach the AP Calc BC exam with confidence and accuracy.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus BC by exploring related units that build on these concepts.
Unit 1

Limits and Continuity
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 4

Contextual Applications of Differentiation
Unit 5

Analytical Applications of Differentiation
Unit 6

Integration and Accumulation of Change
Unit 7

Differential Equations
Unit 9

Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Unit 10

Infinite Sequences and Series
Scroll to Top

Beat AP Calc BC

Make Calculus Click
Before Exam Day
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.