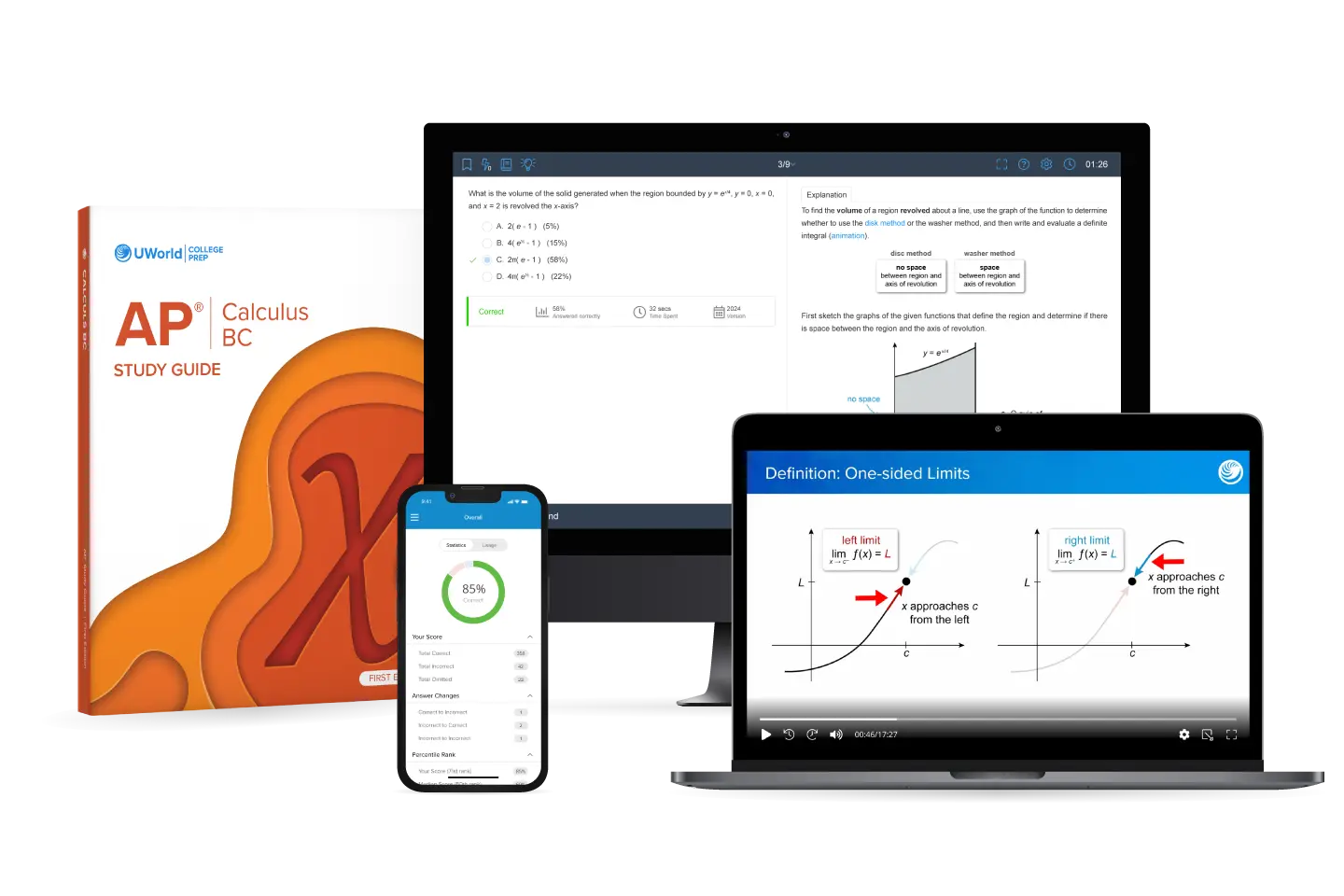
AP® Calculus BC Unit 7 Review and Practice Test
Understand and apply differential equations in AP® Calculus BC Unit 7 with UWorld’s in-depth review course. Learn how derivatives describe dynamic change through modeling, slope fields, and logistic growth. With expert video lessons, visual study guides, and realistic practice tests, UWorld prepares you for both conceptual mastery and exam precision. Strengthen problem-solving skills, analyze real-world models, and gain the confidence to score high on every AP Calc BC Unit 7 question.
Score High in Exam with UWorld’s AP Calculus BC Unit 7 Review
Move beyond memorizing methods by emphasizing reasoning and interpretation, as each lesson walks you through solving differential equations step-by-step while explaining how to read slope fields, apply separation of variables, and model population growth. By combining visual teaching with exam-style practice, UWorld ensures you understand both how and why these equations behave the way they do.
Engage and Learn Differential Equations
Differential equations describe the rate at which systems change, an idea that comes alive with UWorld’s videos. Each video simplifies slope fields, separation of variables, and exponential or logistic models into clear, visual explanations. Watch how a derivative defines the shape of a function or how equilibrium points form in a logistic differential equation. Designed for both review and retention, these lessons align perfectly with the structure of the AP Calc BC Unit 7 exam section.
Interactive Study Guides
UWorld’s interactive study guides for AP Calculus BC Unit 7 take complex ideas and make them accessible. Each topic, such as slope fields, initial value problems, exponential growth, and logistic differential equations, is broken down visually with color-coded steps. By connecting definitions to their graphical and algebraic forms, UWorld helps you understand both symbolic solutions and contextual meaning, an advantage that sets high scorers apart on test day.
Try These AP Calculus BC Unit 7 Practice Test Questions
Question
The number of catfish C raised on a catfish farm grow according to the logistic differential equation , where t is the time in years. If there are 250 catfish at time t = 0, for what value of C is the number of catfish growing most rapidly?
| A. 5000 | |
| B. 1000 | |
| C. 500 | |
| D. 0.4 |
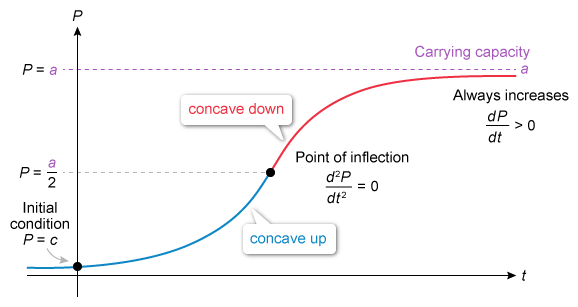
A population P that is modeled by a logistic differential equation is growing most rapidly when P is equal to half the carrying capacity a.
Explanation
A logistic differential equation is of the form ), where P is a population, k is a constant, and a is the upper bound or carrying capacity.
A population P grows most rapidly when the graph of the logistic differential equation changes concavity from up to down at the point of inflection.
The most rapid growth of the population occurs when P is equal to half the carrying capacity a.
To determine the carrying capacity, first rewrite the given equation in the general form of a logistic differential equation.
The general form of a logistic equation has a 1 as the first term in the parentheses, so factor 0.4C out of the parentheses in the given equation.
| Given logistic differential equation | |
| Multiply and divide by 0.4C to factor | |
| Simplify: | |
| Rewrite 0.001 as a fraction to match general form |
Now compare the resulting differential equation to the general form to identify the value of the carrying capacity a.
Divide the carrying capacity a = 1000 by 2 to see that the number of catfish is growing most rapidly when C = 500.
(Choice A) 5000 may result from incorrectly dividing 0.0004 by 0.4 to get a carrying capacity of 10,000.
(Choice B) 1000 is the carrying capacity, but the question asks for the value of C for which the number of catfish is growing most rapidly.
(Choice D) 0.4 is the value of k in the factored form of the given differential equation, but the population grows most rapidly when C is equal to half the carrying capacity a.
Things to remember:
A quantity P with the logistic differential equation
) has its greatest rate of change when P is equal to half the carrying capacity a.
Question
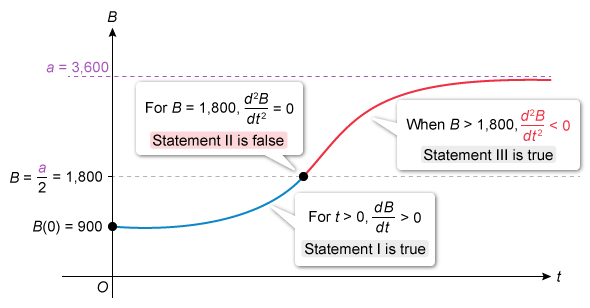
A population of butterflies B grows according to the logistic differential equation ), where t is the time in years and B(0) = 900. Which of the following statements are true?
I. For t > 0, .
II. For B = 900, .
III. When B > 1,800, .
| A. I only | |
| B. II only | |
| C. I and III only | |
| D. I, II, and III |
Consider the graph of the given logistic differential equation to analyze each statement.
Explanation
The solution to a logistic differential equation of the form ) with the initial condition P(0) = c has an upper bound or carrying capacity of a.
The graph of P(t) always increases, so . When , the graph changes concavity from up to down at a point of inflection, so .
To determine which of the statements are true, first compare the given equation to the general form of the logistic differential equation and identify the carrying capacity a.
The carrying capacity of the given equation is a = 3,600. Use the value of a to determine the point of inflection and sketch a graph of the logistic differential equation with the given initial condition of B(0) = 900.
Therefore, only statements I and III are true.
Things to remember:
The general form of the logistic differential equation for the quantity P with carrying capacity a is
).
Question
Let y = f(x) be the solution to the differential equation with initial condition f(2) = 1. What is the approximation for f(1) obtained by using Euler's method with two steps of equal length, starting with x = 2 ?
| A. −1 | |
| B. | |
| C. | |
| D. |
To approximate the y-value of a solution to a differential equation using Euler's method, first determine the step size.
Explanation
Euler's method is a numerical method used to approximate a solution of a differential equation of the form with an initial condition (x0, y0).
To approximate the y-value of a solution using Euler's method with n steps of equal length, apply the following recursive formula n times:
First subtract the given initial x-value (2) from the final x-value (1), and then divide the result by n = 2 to determine the step size .
Set up a table beginning with n = 0 and ending with n = 2, and enter the initial values x0 = 2 and y0 = 1. Add to the x-value from the previous step to get the x-value for the next step.
Now determine the new y-value yn + 1 in each step. Plug the current point (xn, yn) into f ′(xn, yn) = x + 2y, and then plug and the values of f ′(xn, yn) and yn into the Euler's method equation.
The approximation for f(1) obtained by using Euler's method with two steps of equal length, starting with x = 2, is .
(Choice A) is the approximation of ) obtained by using Euler's method with one step, but the question asks for the Euler's method approximation for f(1) with two steps.
(Choice C) is the approximation of ) obtained by using Euler's method with three steps, but the question asks for the Euler's method approximation for f(1) with two steps.
(Choice D) may result from mistakenly calculating Euler's method with a step size of instead of .
Things to remember:
To approximate the y-value of a solution to a differential equation using Euler's method with n steps of equal length, apply the following recursive formula n times:

Take Your Prep Anywhere You Go
Turn every free minute into a productive study session. Whether you’re reviewing slope fields or solving differential equations at your desk, the UWorld app lets you access AP Calc Unit 7 review materials anytime. Practice offline, review mistakes, and track performance across devices, so preparation fits seamlessly into your schedule.
Stand Out
with a Top Score on the AP Calculus BC Exam
Wrap up your AP Calculus BC Unit 7 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students
UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.
The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.
The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
Which major topics fall under “Differential Equations”?
AP Calculus BC Unit 7: Differential Equations centers on how calculus models systems that change continuously. This unit transforms derivative knowledge into tools for predicting behavior across time, motion, and growth. Students learn to write, solve, and interpret equations that describe these dynamic relationships.
The major subtopics include:
- Interpreting verbal descriptions of change as separable differential equations
- Sketching slope fields and families of solution curves
- Using Euler’s method to approximate values on a particular solution curve
- Solving separable differential equations to find general and particular solutions
- Deriving and applying exponential and logistic models
Each of these areas appears on the AP Exam in both multiple-choice and free-response sections. UWorld’s AP Calculus BC Unit 7 Review walks you through each concept visually and analytically, showing how rate-based relationships evolve into full models. By mastering how to interpret differential equations graphically and algebraically, you’ll gain the precision needed for every exam section. UWorld’s detailed step-by-step solutions help you connect the calculus to its meaning, ensuring that solving becomes intuitive, not mechanical.
How should I prepare for an AP Calculus BC Unit 7 exam?
Preparing for AP Calc BC Unit 7 requires equal focus on conceptual understanding and repetitive, structured practice. Differential equations test your ability to explain why systems behave as they do, not just how to solve them. The best strategy involves layering your preparation, starting with concept clarity and then applying it through timed problem-solving.
Follow this structured plan:
- Step 1: Learn visually. Watch UWorld’s differential equation videos to understand slope fields and the separation of variables conceptually.
- Step 2: Reinforce understanding. Review UWorld’s AP Calculus BC Unit 7 Review Study Guide to summarize definitions, formulas, and key methods.
- Step 3: Practice strategically. Attempt multiple practice test sets to simulate AP-style questions under real-time conditions.
- Step 4: Analyze performance. Use UWorld’s analytics to identify weak areas, such as interpreting slope fields or solving logistic models, and reattempt them until you achieve consistency.
The key is building comfort with both symbolic and contextual thinking. UWorld’s explanations don’t stop at the math as they explain the reasoning behind every step. By exam day, you’ll recognize question structures immediately and know exactly how to start, saving time and reducing anxiety.
How much time should I spend reviewing Unit 7 before the exam?
Time management is critical for AP Calculus BC Unit 7, which demands both conceptual retention and repeated exposure to applied problems. Ideally, dedicate 8-12 focused hours over 2 weeks solely to Unit 7 topics before your AP Exam. Spread this time evenly to balance comprehension, application, and review.
Start with 2-3 hours revisiting the key concepts, such as slope fields, separation of variables, and logistic differential equations. Use UWorld’s videos and study guides to refresh the “why” behind each formula. Next, devote 4-5 hours to hands-on problem-solving using AP Calculus BC Unit 7 practice test sets. Aim to complete questions in timed batches and always review every rationale afterward, even for correct answers.
In your final sessions, transition to an integrated review by mixing Unit 7 problems with earlier differentiation and integration topics. This simulates the AP Exam’s cumulative nature and builds agility across question types. UWorld’s Check-for-Understanding questions are especially helpful for quick diagnostics, as they efficiently flag any conceptual gaps.
By following this schedule, you’ll ensure not just recall but real fluency. Students who practice daily tend to retain more information and enter the exam with a calm, logical rhythm, which improves both accuracy and pacing.
Are any free resources available for AP Calculus BC Unit 7?
Yes. UWorld’s 7-day free trial provides access to AP Calculus BC Unit 7 review videos and practice questions, crafted to mirror actual exam rigor. Each question includes detailed explanations that not only give correct solutions but also unpack why those solutions work.
Additionally, the College Board’s AP Classroom platform provides topic outlines, sample problems, and videos that explain core concepts, such as slope fields and logistic growth. While these are helpful introductions, they tend to focus more on content coverage than exam performance.
To make the most of your free study time:
- Review one topic video per session, focusing on conceptual clarity rather than just formulas.
- Attempt a small set of practice problems and read through every explanation carefully.
- Revisit UWorld’s notes to avoid frequent student pitfalls, especially in slope interpretation and variable separation.
This combination of structured free materials and insight-driven reasoning gives you a measurable advantage. Even before upgrading to full access, the free UWorld resources help you build confidence, identify weak spots, and approach Unit 7 AP Calc BC with the analytical mindset the AP Exam expects.
What types of questions are on the AP Calculus BC Unit 7 test?
The AP Calculus BC Unit 7 test emphasizes conceptual modeling and interpretation. Questions go beyond computation, asking you to explain what differential equations represent and how they connect to real-world change. You’ll see both multiple-choice and free-response questions that test your ability to identify, construct, and solve relationships between functions and their rates.
Common question types include:
- Determining solution behavior from slope fields or graphs.
- Solving separable differential equations symbolically and verifying results.
- Modeling population, cooling, or growth scenarios with exponential or logistic equations.
- Interpreting constants, equilibrium points, and limits in context.
FRQs often require justification, where you’re showing not just the math but your reasoning. A single word or phrase can distinguish between partial and full credit, so clarity matters as much as computation.
UWorld’s AP Calculus BC Unit 7 review problems mirror this balance exactly. Each explanation breaks down both the procedural and interpretive logic, ensuring you practice the same depth expected on the AP Exam. After several rounds of timed quizzes and review cycles, you’ll recognize recurring structures and know instinctively how to approach each type.
How can I improve my score on the FRQs and MCQs for Unit 7?
Improving your FRQ and MCQ performance in AP Calc BC Unit 7 depends on precision, reasoning, and familiarity with question structure. Many students know how to compute derivatives but struggle to apply them within differential contexts, and this is where UWorld bridges the gap.
Focus on these two targeted strategies:
- For MCQs: Prioritize efficiency. UWorld’s AP Calculus BC Unit 7 Review includes step-level rationales showing which variables to isolate and which to ignore. Regular exposure trains your eye to quickly spot slope-field trends and logistic models.
- For FRQs: Emphasize explanation. AP graders reward clear reasoning. Use complete sentences to justify differential equation steps, reference units, and interpret the meaning in context. UWorld’s FRQ-style questions guide you in writing concise yet mathematically accurate justifications.
By alternating between both formats, you strengthen comprehension and adaptability. UWorld’s timed quiz mode simulates exam pacing, while post-session analytics reveal weak areas in real time. This data-driven feedback cycle ensures every session builds measurable improvement. Over several weeks, accuracy stabilizes, speed increases, and your written reasoning becomes naturally concise, qualities that consistently translate to higher AP Exam scores.
What is the "Differential Equations" unit's weight on the AP Calculus BC exam?
AP Calculus BC Unit 7: Differential Equations typically makes up 6-9% of the total AP Exam score. While that may seem modest, its impact is larger than the number suggests because it directly connects multiple major calculus concepts, such as derivatives, integration, and modeling. Questions involving slope fields, initial value problems, or logistic growth appear across both the multiple-choice and free-response sections.
This unit functions as a bridge between abstract calculus and real-world applications. On FRQs, you’ll often see one question partially or fully dedicated to differential equations, requiring you to describe solution behavior, find particular solutions, and interpret the meaning within context. Similarly, multiple-choice sections test whether you can link differential forms to their geometric and functional interpretations.
UWorld’s AP Calculus BC Unit 7 Review ensures you’re not just memorizing procedures but internalizing the connections. The review course highlights patterns that often recur in FRQs, such as identifying equilibrium points in logistic equations or verifying differential solutions through substitution. By learning these skills now, you’ll also strengthen performance in later exam topics such as integration and series convergence. Differential equations may represent a smaller slice of the test, but they distinguish fluent problem-solvers from surface learners.
What’s the best way to organize my formula sheet for integrals?
While AP Calc BC Unit 7 doesn’t focus solely on integrals, the integration techniques you’ve learned are essential for solving separable differential equations. A well-organized formula sheet acts as a quick mental map rather than a memorization tool, helping you recall relationships logically instead of hunting for disconnected facts.
Here’s how to structure it effectively:
- Group by function type: Separate trigonometric, exponential, and rational functions, labeling each with the corresponding antiderivative.
- Include common patterns: List forms alongside brief notes on their typical application.
- Highlight separation patterns: Annotate the integral setup and general solution form.
- Add reminder notes: Include steps for initial value problems, like integrate, apply constant, substitute known point, verify.
When paired with UWorld’s AP Calculus BC Unit 7 Review, your sheet becomes a reflection of understanding, not dependency. Reviewing it regularly ensures fluency under exam conditions. The goal isn’t to memorize every formula, but to recognize patterns quickly and understand how each connects to solving absolute differential equations efficiently.
How much time should I spend reviewing Unit 7 before the exam?
Students preparing for Unit 7 AP Calculus BC should plan to invest 10-12 total hours of structured review time over the two weeks preceding the AP Exam. This unit’s concepts: slope fields, separable equations, and logistic models require both repetition and conceptual thinking.
Break your review into three phases:
- Phase 1 (Concept Refresh): Spend 3-4 hours reviewing fundamentals using UWorld’s videos and annotated notes. Focus on understanding why differential equations model change.
- Phase 2 (Active Practice): Dedicate 5-6 hours to solving UWorld’s ap calculus bc unit 7 practice test questions, analyzing rationales, and identifying conceptual patterns.
- Phase 3 (Integration Review): Use 2-3 hours to mix Unit 7 problems with earlier differentiation and integration units. This simulates the interconnectedness of real exam questions.
Throughout your schedule, focus on spaced repetition rather than long sessions. UWorld’s dashboard and check-for-understanding quizzes enable you to assess your readiness daily, providing instant feedback on your strengths and areas for improvement. With consistent pacing and active feedback, 10 focused hours can transform into deep familiarity and fast recall under pressure.
How can I use UWorld to prepare for AP Classroom’s Progress Check MCQs and FRQs?
The College Board designs the AP Classroom progress checks to measure concept mastery within each unit, including AP Calculus BC Unit 7. While these aren’t part of the official exam, they closely reflect its structure and question logic. UWorld’s learning system complements these checks perfectly, and helps you not only score well on them but also build deeper exam readiness.
Each topic in UWorld’s AP Calculus BC Unit 7 review includes “Check-for-Understanding” questions similar in intent to progress check MCQs. They assess immediate comprehension of slope fields, separation of variables, and logistic differential equations. Completing them after each study session ensures you’re retaining what you’ve learned and spotting weak areas early.
When you later attempt official progress checks, the patterns will feel familiar because UWorld’s problems are written at the same analytical level and use identical phrasing cues. The FRQ-style questions further train you to explain solutions clearly and justify reasoning concisely, improving both progress check and exam performance.
By pairing these systems, students turn routine assignments into high-yield prep. You’re not just reviewing for class; you’re refining the analytical skills and confidence needed for full-length AP Exam success.
Where can I find a good study guide for AP Calculus BC Unit 7?
A strong AP Calculus BC Unit 7 study guide should do more than list formulas and help you understand how differential equations behave and how they connect to other calculus concepts. While textbooks and online summaries cover the basics, they often skip the reasoning that the AP Exam requires: explaining why solutions make sense in context.
UWorld’s interactive study guides fill that gap by blending visual learning with exam-style explanation. Each section begins with conceptual breakdowns, such as what slope fields represent, how to separate variables, and how logistic models describe realistic limits on growth. Then, it transitions into annotated examples that parallel real AP Exam questions.
Each page of UWorld’s AP Calculus BC Unit 7 Review emphasizes reasoning, not rote memorization. Notes and callouts within explanations highlight “exam traps,” clarifying why specific steps are practical and others are not. This combination of conceptual clarity and visual learning is ideal for last-minute review sessions or deeper study.
Whether you prefer print or digital, UWorld’s study guide gives you a roadmap, showing how Unit 7 connects earlier derivative concepts to later integration and series topics. It’s structured for students who want not just to solve equations but understand the logic driving them, which is precisely what high-scoring responses demonstrate on test day.
Can I find practice tests specifically for AP Calc BC Unit 7?
Yes. Several practice options exist for AP Calculus BC Unit 7, but the key is finding those that match the AP Exam’s style and difficulty. While some general calculus platforms offer mixed practice, UWorld’s targeted question sets for Differential Equations replicate the pacing, structure, and complexity of the real test.
Each AP Calculus BC Unit 7 practice test in UWorld’s library includes slope field interpretation, separation of variables, and logistic model applications. What makes these unique is their dual focus on exam readiness and conceptual depth. Every question comes with color-coded solution steps that explain how to move from setup to interpretation, not just computation.
To maximize results, take one short quiz daily (5-10 questions), then one full-length Unit 7 test weekly. Use UWorld’s performance analytics to track your accuracy, time spent, and conceptual errors. Over time, you’ll notice patterns like confusing rate signs or missing constants, and UWorld’s built-in notes feature lets you flag those instantly.
Practicing with exam-level materials ensures you enter the test familiar with every question format. By combining repetition, analysis, and immediate feedback, UWorld transforms simple practice into measurable improvements on exams.
What are the most common mistakes students make on Unit 7 questions?
Students often underestimate the conceptual nature of Unit 7 AP Calc BC questions. The most frequent mistakes occur when they treat differential equations mechanically rather than interpretively. Many know how to separate variables or integrate, but fail to connect results to real-world meaning, which is a key expectation on the AP Exam.
Common pitfalls include:
- Ignoring context: Students solve problems correctly but can’t explain what their solution represents in terms of growth or decay scenarios.
- Mishandling slope fields: Misreading direction patterns or failing to recognize equilibrium lines leads to incorrect interpretations.
- Forgetting constants or initial conditions: Missing “+C” terms or incorrect substitutions reduce full-credit FRQs to partial.
- Confusing logistic and exponential models: Students forget that logistic equations flatten near the carrying capacity, unlike exponential ones.
UWorld’s AP Calculus BC Unit 7 review helps eliminate these errors by teaching reasoning alongside procedure. Each question highlights not just how to solve but how to interpret. With repeated exposure, students begin to predict behavior, rather than just calculate it, which is a critical shift that leads to greater accuracy, clarity, and higher scores.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Applications of Integration
Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Infinite Sequences and Series