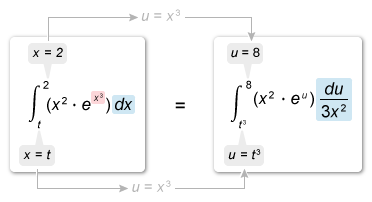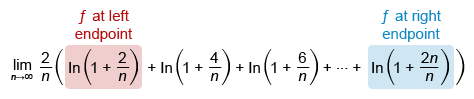Bundle 3+ College Prep products for 20% off

AP® Calculus BC Unit 6 Review and Practice Test

Integration and Accumulation of Change

If you’re preparing for AP® Calculus BC Unit 6, this guide helps you build a solid grasp of integration and accumulation concepts—core ideas that connect everything you’ve learned about change, motion, and area. Through guided practice, step-by-step examples, and exam-style questions, you’ll strengthen your problem-solving skills and get exam-ready with confidence.

AP Calculus BC prep course suite by UWorld

Strengthen Your Skills with Our AP Calculus BC Unit 6 Review

Learn how integration connects rates of change and accumulated quantities in real-world contexts. This AP Calc BC Unit 6 review breaks down key techniques, builds problem-solving confidence, and prepares you for success on the AP exam.

Watch

Engaging Video Lessons

Watch step-by-step explanations of integration techniques, including substitution, partial fractions, and integration by parts. These AP Calculus BC Unit 6 videos simplify complex topics and show how each method applies to real problems. Perfect for reviewing before practicing your AP Calc BC Unit 6 progress check MCQ Part A.

Preview Video Lesson
Buy Now
UWorld’s AP Calc BC Video Lessons
UWorld’s AP Calculus BC Study Guide Prep book
Read

Interactive Study Guides

Explore AP Calculus BC Unit 6 study guides that break down integration and accumulation of change into easy-to-follow steps. These interactive guides cover essential formulas, substitution rules, and integration by parts methods. Perfect for your unit 6 AP Calc BC review, they include visuals, examples, and practice tips to help you retain concepts and perform better on your exam.

Preview Book
Buy Now
Practice

Challenge Yourself with AP Calculus BC Unit 6 Practice Questions

Test your understanding of integration and accumulation concepts with realistic AP Calc BC Unit 6 practice questions. Each problem mirrors the difficulty of the actual exam, from substitution and parts to complex integration techniques. Use these exercises to strengthen problem-solving speed and accuracy before your AP Calculus BC Unit 6 progress check MCQ Part A and FRQs.
Try these sample practice questions with detailed answer explanations:
Integration and Accumulation of Change Practice Tests

Question

∫ x 3 cos x d x =

A. 3 x 2 sin x - ∫ x 3 sin x d x
B. x 3 sin x - 3 ∫ x 2 sin x d x
C. 1 4 x 4 sin x + C
D. 1 4 x 4 cos x + x 3 sin x + C
Hint :
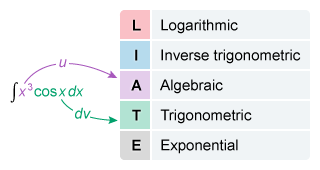
The functions cannot be rewritten algebraically or with u-substitution, so use integration by parts.

Explanation

The given integrand is the product of the functions x 3 and cos x. The functions cannot be rewritten algebraically or with u-substitution, so use integration by parts.

function of the limbic system structure

Follow the LIATE acronym to select u. Algebraic expressions (x3) are above trigonometric expressions (cos x),so let u = x3 and let dv = cos x dx (the remaining parts of the integrand).

function of the limbic system structure

Differentiate u = x3 and solve for du (see how), and integrate dv = cos x dx to find v.  Substitute u = x3, v = sin x, and du = 3x2 dx into the formula for integration by parts and simplify.

u v - ∫ v d u Integration by parts formula
x 3 ( (sin x) - ∫ (sin x) (3 x 2 d x) Plug in u = x3, v = sin x, and du = 3x2 dx
x 3 sin x - 3 ∫ x 2 sin x d x Simplify and apply constant multiple rule

Notice that the resulting expression matches one of the choices, so it is not necessary to integrate ∫ x 2 cos x d x .  From integration by parts, the given integral is equal to x 3 sin x - 3 ∫ x 2 sin x d x .

(Choice A)  3 x 2 sin x - ∫ x 3 sin x d x may result from mistakenly switching the expressions for u and du when substituting into the formula for integration by parts.

(Choice C)  1 4 x 4 sin x + C may result from mistakenly integrating each function in the given product individually.

(Choice D)  1 4 x 4 cos x + x 3 sin x + C may result from mistakenly applying the product rule for differentiation.

Things to remember:
If the integral of the product of two functions cannot be evaluated by u-substitution, use integration by parts:

∫ u d v = u v - ∫ v d u

Question

∫ - ∞ 2 x 2 e x 3 dx

A. e 8 3
B. e8
C. 3e8
D. divergent
Hint :
An improper integral of the form ∫ - ∞ 2 f (x) dx converges if lim t → - ∞ ∫ t 2 f (x) dx exists.

Explanation

An integral in which one or both limits of integration is infinite is an improper integral.

To evaluate an improper integral of this form, replace the infinite limit of integration with the variable t and then calculate the limit as t approaches −∞ .

∫ - ∞ 2 x 2 e x 3 dx = lim t → - ∞ ∫ t 2 x 2 e x 3 dx

The integrand contains a composite function of the form eu, where u = x3.  To use u-substitution, first differentiate u = x3 with respect to x and solve for dx to get du 3 x 2 = dx (calculation).

The limits of integration must be changed to values of u, so plug the limits of integration into u = x3 to rewrite them as values of u.  Substitute x3 = u, dx = du 3 x 2 , and the new limits of integration into the given integral.

activation synthesis hypothesis

Now simplify the resulting integral to eliminate the remaining x-terms, integrate, and apply the Fundamental Theorem of Calculus (FTC).

∫ t 3 8 (x 2 ⋅ e u ) du 3 x 2 Resulting integral in terms of u
1 3 ∫ t 3 8 e u du Cancel and apply constant multiple rule
1 3 e u | t 3 8 Integrate natural exponential function
1 3 (e 8 - e t 3 ) Apply FTC

Substitute the result above into the limit expression for the desired improper integral.

lim t → - ∞ ∫ t 2 x 2 e x 3 dx Improper integral rewritten as a limit
lim t → - ∞ (   1 3  (e 8 - e t 3  )  ) Substitute ∫ t 2 x 2 e x 3 dx = 1 3 ( e 8 - e t 3 )
1 3 lim t → - ∞ (e 8 - e t 3 ) Apply constant multiple rule for limits
1 3 (e 8 - 0) Evaluate: lim t → - ∞ e t 3 = 1 e ∞ 3
e 8 3 Simplify

Therefore, the value of the given integral is e 8 3 .

(Choice B)  e8 may result from mistakenly substituting dx = du x 2 (instead of dx = du 3 x 2 ) when rewriting the integral in terms of u.

(Choice C)  3e8 may result from mistakenly bringing out a constant multiple of 3 (instead of 1 3 ) when applying u-substitution.

(Choice D)  "Divergent" may result from assuming that an infinite limit of integration does not converge.

Things to remember:
To evaluate an improper integral, rewrite it as the limit of a definite integral:

∫ - ∞ a f (x) dx = lim t → - ∞ ∫ t a f (x) dx

Question

Which of the following expressions is equal to lim n → ∞ 2 n  ( ln ( 1 + 2 n )+ ln (1 + 4 n )+ ln (1 + 6 n )+ … + ln (1 + 2 n n ) ) ?

A. ∫ 0 2 ln x dx
B. ∫ 1 3 ln x dx
C. ∫ 0 1 ln (1 + x) dx
D. ∫ 1 3 ln (1 + x) dx
Hint :
The value of a definite integral ∫ a b f (x) dx can be expressed in the form lim n → ∞ ∑ i = 1 n f( a + Δ xi) Δ x , which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width ∆ x = b - a n .

Explanation

The value of a definite integral ∫ a b f (x) dx can be expressed in the form lim n → ∞ ∑ i = 1 n f (a + Δ xi) Δ x , which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width ∆ x = b - a n :

somatosensation

The given limit appears to be in the form of the limit of a right Riemann sum where f (a + Δ xi) = ln (1 + 2 n i) and ∆ x = 2 n .  First, verify that the general function is f (a + Δ xi) = ln (1 + 2 n i) and the subinterval width is ∆ x = 2 n (see how).

As n approaches infinity, the first term in a right Riemann sum approaches f(a), the value of f at the left endpoint of the interval [a, b].  The last term equals f(b), the value of f at the right endpoint of [a, b] (read more).

somatosensation

The left endpoint of the interval a is the lower limit of integration, and the right endpoint b is the upper limit of integration.

To determine which choice has the correct integrand f(x) and limits of integration [a, b], evaluate the limit as n approaches infinity of the first and last terms to find f(a) and f(b).

f(a) = lim n→∞ ln ( 1+ 2n ) Limits of first and last terms f(b) = lim n→∞ ln ( 1+ 2n n )
f(a) = lim n→∞ ln ( 1+ 2n ) Cancel n in right limit f(b) = lim n→∞ ln ( 1+2 )
f(a) = ln ( 1+0 ) Evaluate limits f(b) = ln ( 1+2 )
f(a) = ln1 Add f(b) = ln3

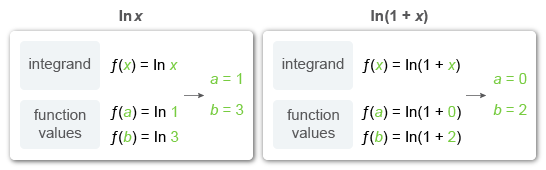
The choices include two possible integrands ln x and ln(1 + x).  The values of f(a) and f(b) could correspond to either integrand, so find the values of a and b that yield ln 1 and ln 3, respectively, for each integrand.

somatosensation

The given limit must equal ∫ 1 3 ln x dx or ∫ 0 2 ln (1 + x ) dx .  Of these two integrals, only ∫ 1 3 ln x dx is an answer choice.

(Choice A)  ∫ 0 2 ln x dx may result from incorrectly calculating limits of integration for the integrand ln x.

(Choice C)  ∫ 0 1 ln (1 + x ) dx may result from incorrectly calculating the upper limit of integration for the integrand ln(1 + x).

(Choice D)  ∫ 1 3 ln (1 + x) dx may result from incorrectly calculating limits of integration for the integrand ln(1 + x).

Things to remember:
The value of a definite integral ∫ a b f (x) dx can be expressed in the form lim n → ∞ ∑ i = 1 n f (a + Δ xi) Δ x , which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width ∆ x = b - a n .

Buy Now
UWorld Dark Blue logo

Learn Anytime, Anywhere

Whether you’re on your way to class, taking a study break, or relaxing at a café, keep your prep going with the UWorld app. Access AP Calculus BC Unit 6 review materials, video lessons, and practice tests anytime to stay consistent and confident with your integration and accumulation concepts.

App Store
Google Play

Stand Out
with a Top Score on the AP Calculus BC Exam

Wrap up your AP Calculus BC Unit 6 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc BC Videos
  • Print & Digital Study Guide
  • 1800+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards & Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calculus BC Unit 6 focuses on understanding how integration models change and accumulation in mathematical and real-world contexts. It builds essential skills for solving complex integral problems efficiently.

Key topics include:

  • Using definite integrals to calculate accumulated change over a specific interval.
  • Approximating integrals with Riemann Sums to estimate areas and totals when exact values are hard to find.
  • Exploring accumulation functions, the Fundamental Theorem of Calculus, and how they connect derivatives and integrals.
  • Finding antiderivatives and indefinite integrals to reverse differentiation and represent families of functions.
  • Applying properties of integrals and extended integration techniques to simplify complex problems.
  • Determining improper integrals to evaluate infinite intervals or unbounded functions.

With UWorld’s AP Calculus BC Unit 6 review and practice questions, you can strengthen each of these skills through clear explanations and step-by-step examples that mirror real AP Calc BC Unit 6 test problems.

Preparing for the AP Calculus BC Unit 6 exam is most effective when you follow a simple cycle: read, watch, and practice. Start by reading through your notes and AP Calc BC Unit 6 review materials to revisit integration rules, the Fundamental Theorem of Calculus, and accumulation concepts.

Next, watch AP Calculus BC Unit 6 video lessons that break down substitution, integration by parts, and other key techniques. Visual learning helps you see how formulas are applied and improves your problem-solving approach.

Finally, practice using AP Calc BC Unit 6 progress check MCQ Part A and FRQ questions to test your understanding under exam-like conditions. With UWorld’s AP Calculus BC Unit 6 practice tests and interactive explanations, you can identify weak areas, learn from mistakes, and build confidence for the real exam.

For AP Calculus BC Unit 6, plan at least one week of focused review to master integration and accumulation of change. Dedicate separate sessions for definite integrals, Riemann Sums, and integration techniques like substitution or parts. Reviewing smaller topics daily helps retain concepts and reduces stress closer to exam day.

Balance your time between reading theory and solving problems. Try working through a few AP Calc BC Unit 6 progress check MCQ Part A and FRQ questions each day to track improvement and identify gaps in understanding.

If you’re unsure how to organize your prep, UWorld’s AP Calculus BC Unit 6 review materials make it simple. With structured lessons, practice tests, and step-by-step solutions, UWorld helps you use your study time efficiently and feel fully prepared for the AP Calc BC Unit 6 test.

Yes! There are several great free resources to help you prepare for AP Calculus BC Unit 6. Start with Khan Academy, which offers clear video tutorials and interactive exercises on integration, Riemann Sums, and accumulation functions. It’s a great way to refresh concepts before diving into practice.

The College Board website also provides official AP Calculus BC materials, including Unit 6 progress check MCQs and FRQs, sample questions, and scoring guidelines. Reviewing these helps you understand the format and difficulty of actual exam questions.

For more in-depth practice, try UWorld’s free trial for AP Calculus BC Unit 6 review. You’ll get access to realistic questions, detailed solutions, and integration-focused study tools that make complex topics easier to understand—helping you build confidence and accuracy before test day.

The AP Calculus BC Unit 6 test includes a mix of multiple-choice and free-response questions (FRQs) that test your understanding of integration and accumulation of change. You’ll encounter problems on definite and indefinite integrals, accumulation functions, and the Fundamental Theorem of Calculus.

Expect to solve questions involving Riemann Sums, substitution, integration by parts, and improper integrals. Some questions require interpreting graphs, while others involve applying formulas to real-world rate and area problems. Knowing when to use a calculator is also important—some parts of the exam allow one, while others don’t.

To prepare effectively, use UWorld’s AP Calculus BC Unit 6 practice tests and review materials. Each question includes step-by-step explanations that mirror real exam problems, helping you strengthen problem-solving skills and gain confidence for your AP Calc BC Unit 6 progress check MCQ Part A and FRQ.

To score higher on the AP Calculus BC Unit 6 FRQs, focus on clarity, setup, and correct reasoning. Always show your work; even partial solutions can earn points. Review how to apply the Fundamental Theorem of Calculus and integration techniques like substitution and integration by parts, as these often appear in FRQs.

Practice writing complete responses under timed conditions. Many FRQs combine concepts such as accumulation functions, area under curves, and rate of change problems, so make sure you understand how to interpret each scenario mathematically.

Use UWorld’s AP Calculus BC Unit 6 review and practice questions to get familiar with the question format and scoring style. With detailed solutions and exam-style prompts, UWorld helps you identify common errors, refine explanations, and build the confidence needed to excel on test day.

The “Integration and Accumulation of Change” unit makes up about 17–20% of the AP Calculus BC exam, making it one of the most heavily tested sections. It covers key concepts like definite integrals, accumulation functions, and integration techniques, which are vital for solving real-world rate, area, and motion problems.

Expect multiple-choice and free-response questions that test your understanding of the Fundamental Theorem of Calculus, antiderivatives, and improper integrals. These skills also serve as a foundation for advanced units such as Differential Equations and Infinite Series.

Strengthen your grasp of these topics with UWorld’s AP Calculus BC Unit 6 review, featuring realistic progress check MCQs and FRQs that simulate the exam format and help you gain the precision and confidence needed for a top score.

A well-organized formula sheet helps you recall key integration concepts quickly during your AP Calculus BC Unit 6 review. Start by grouping formulas by type: basic integration rules, substitution, integration by parts, partial fractions, and trigonometric integrals. This structure helps you identify which technique applies to a given problem.

Next, include common antiderivatives and key relationships from the Fundamental Theorem of Calculus. Keep your notes clean and minimal; focus on formulas you tend to forget or confuse. Use color-coding or symbols to highlight patterns between related functions.

As you practice with UWorld’s AP Calculus BC Unit 6 progress check MCQ and FRQ-style questions, refine your formula sheet to focus on areas where you make mistakes. Over time, it becomes not just a study tool but a quick-reference guide that sharpens accuracy and speed.

UWorld’s AP Calculus BC Unit 6 review and practice questions are a great starting point for anyone looking for a reliable study guide. With its structured learning path, UWorld helps you build a deeper understanding of differentiation topics like the chain rule, implicit differentiation, and derivatives of inverse functions. The detailed explanations, visual solutions, and question-level feedback make complex ideas easier to grasp. Whether you’re studying for the AP Calculus BC Unit 6 test or brushing up before your final exam, UWorld’s comprehensive study guide and free trial provide the support you need to master this unit.

In addition to UWorld, you can strengthen your preparation with trusted academic resources and classroom materials that summarize formulas, show worked examples, and highlight common student mistakes. Websites like Khan Academy offer concise AP Calc BC Unit 6 review notes with topic explanations and short quizzes for quick practice. The College Board’s AP Classroom also features Unit 3 progress check MCQs and FRQs that mirror the format of real exam questions, making them ideal for self-assessment.

Many students lose points on AP Calculus BC Unit 6 questions by confusing definite and indefinite integrals or forgetting to apply the Fundamental Theorem of Calculus correctly. Others make algebraic or sign errors when using integration techniques like substitution or integration by parts.

Another common mistake is misinterpreting accumulation function graphs or neglecting to include the constant of integration when finding antiderivatives. Students also struggle with setting up Riemann sums and improper integrals, which can affect both accuracy and time management.

To avoid these pitfalls, review worked examples, check your setup before solving, and practice under timed conditions. UWorld’s AP Calculus BC Unit 6 review offers detailed explanations and instant feedback, helping you recognize and fix these errors before exam day.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus BC by exploring related units that build on these concepts.
Unit 1

Limits and Continuity
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 4

Contextual Applications of Differentiation
Unit 5

Analytical Applications of Differentiation
Unit 7

Differential Equations
Unit 8

Applications of Integration
Unit 9

Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Unit 10

Infinite Sequences and Series
Scroll to Top

Beat AP Calc BC

Make Calculus Click
Before Exam Day
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.