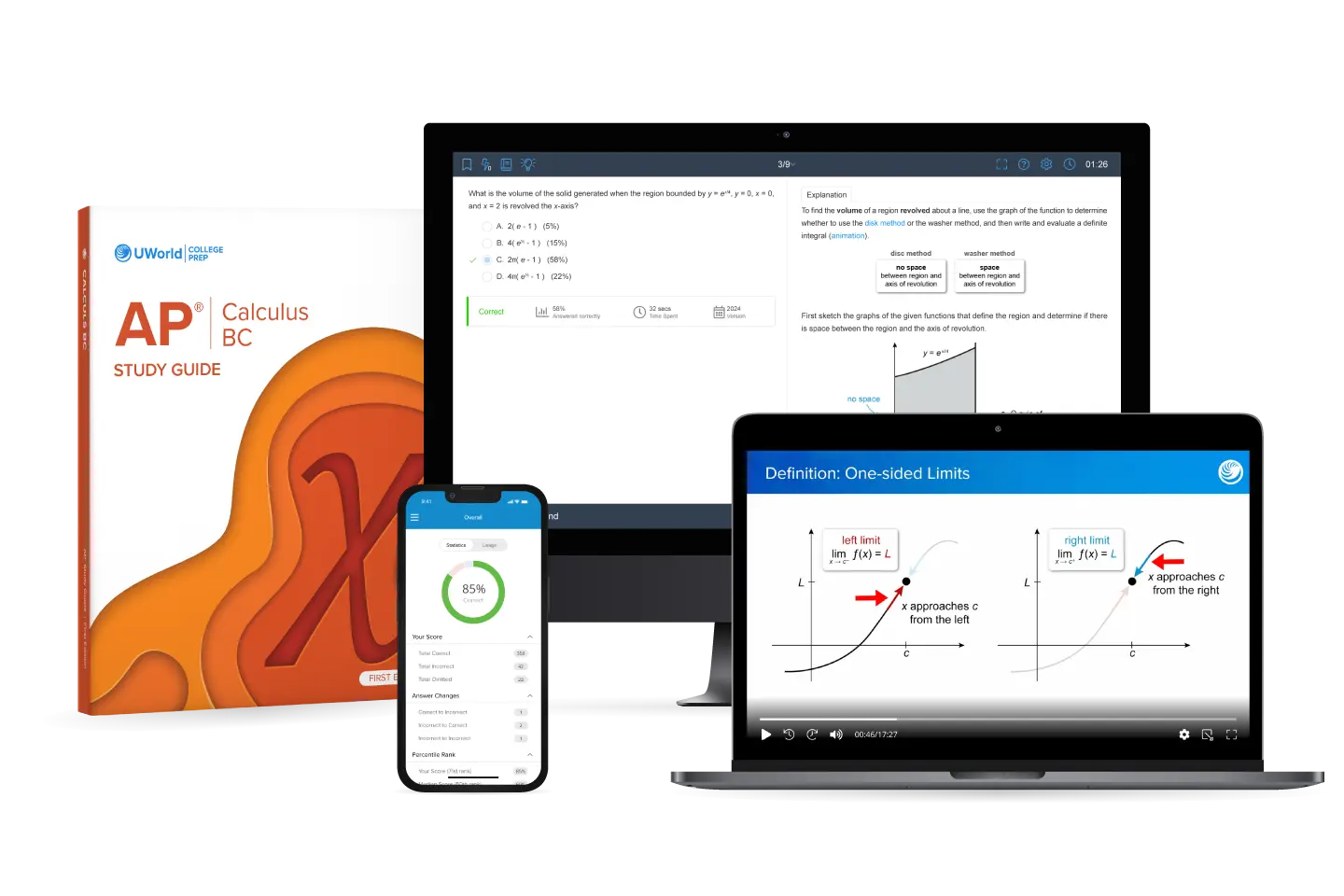
AP® Calculus BC Unit 4 Review and Practice Test
Excel in AP® Calculus BC Unit 4 by mastering how derivatives model motion, optimization, and real-world rates of change. UWorld’s AP Calc BC Unit 4 review combines expert instruction, visual study tools, and authentic exam-style questions to strengthen understanding and improve your AP score. From related rates to acceleration, every concept is taught for depth, accuracy, and speed under exam conditions.
Ace the Derivative Applications on the Exam with UWorld’s AP Calculus BC Unit 4 Review
Learn to interpret and apply derivatives to solve real-world problems through UWorld’s complete AP Calc BC Unit 4 prep course. Each explanation ties theory to practical application so you can tackle the AP Exam confidently. Whether calculating velocity, finding extrema, or analyzing concavity, you’ll approach every problem methodically with precision that earns points.
Learn with Engaging Video Lessons
Bring Calculus to life with concise, visual videos that simplify even the most abstract Unit 4 concepts. Each video demonstrates exactly how to structure solutions the AP Exam expects, helping you bridge understanding and execution in AP Calculus BC Unit 4 topics.
Interactive Study Guides for Faster Learning
UWorld’s AP Calculus BC Unit 4 review materials turn complex derivative applications into structured, easy-to-follow lessons See how each topic links to real AP Exam problems and practice writing clear, concise reasoning, which is an essential skill for both FRQs and MCQs.
Sharpen Your Skills with Realistic AP Calculus BC Unit 4 Questions
Question
A particle is moving along the x -axis with position given by At what time t in the interval is the particle's instantaneous velocity equal to its average velocity over the interval ?
| A. 0 | |
| B. | |
| C. | |
| D. 9 |
Hint :
The Mean Value Theorem guarantees the existence of at least one value of x=c in the closed interval [a,b] for which the instantaneous rate of change of a continuous and differentiable function f(x) equals the average rate of change of f on [a,b] .
Explanation
The velocity v(t) of a moving particle is given by the derivative of the particle's position function x(t) .
Since velocity is the derivative of position, the instantaneous velocity is the instantaneous rate of change of the position x . Similarly, the average velocity is the average rate of change (AROC) of the position x .
The Mean Value Theorem (MVT) guarantees that there exists at least one value of x in the closed interval [a,b] for which the instantaneous rate of change (IROC) of a continuous and differentiable function f(x) equals the average rate of change (AROC) of f on [a,b] .
To determine the value of t = c for which the instantaneous velocity equals the average velocity of the particle on the given interval, first differentiate the position function to find an equation for the instantaneous velocity to find an equation for the instantaneous velocity .
| Given position function | |
| Rewrite | |
| Differentiate: | |
| Simplify and rewrite and |
To calculate the average velocity of on , use the formula for average rate of change with the given function x:
| AROC formula | |
| Plug in a = 0 and b = 9 | |
| Evaluate for t = 0 and t = 9 | |
| Take the square root of 9 and 0 | |
| Simplify |
Now set the expression for the instantaneous velocity equal to the average velocity and solve for t.
| Set the instantaneous velocity = average velocity | |
| Substitute and | |
| Cross multiply | |
| Divide both sides by 2 | |
| Square both sides |
Therefore, the value of t in the interval 0 ≤ t ≤ 9 for which the particle's instantaneous velocity equals its average velocity is
(Choices A and D) 0 and 9 may result from the assumption that the particle's instantaneous velocity and average velocity are equal at one of the endpoints.
(Choice B) may result from setting the given position function x(t) , instead of the instantaneous velocity function x′(t) , equal to the average velocity.
Things to remember:
- The velocity of a moving particle is given by the derivative of the particle's position function. .
- The conclusion of the Mean Value Theorem guarantees the existence of at least one value x=c in the open interval (a,b) at which the instantaneous rate of change of a continuous function f(x) is equal to the average rate of change of f on the interval [a,b]
Question
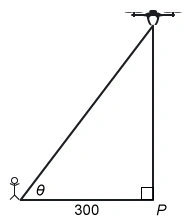
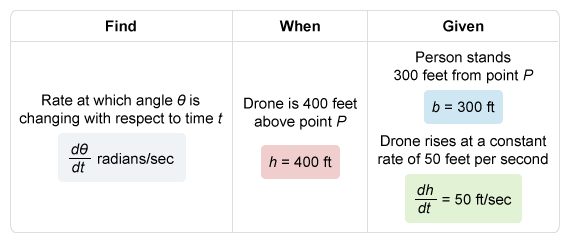
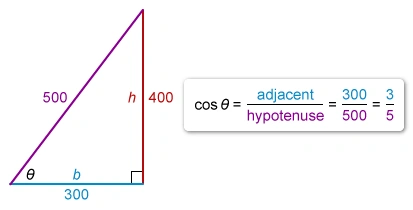
A person stands 300 feet from point P and watches a drone rise vertically from the point, as shown in the figure above. The drone is rising at a constant rate of 50 feet per second. What is the rate of change, in radians per second, of angle θ at the instant when the drone is 400 feet above point P ?
| A. | |
| B. | |
| C. | |
| D.
|
Hint :
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Explanation
To find a quantity when given the rates at which multiple variables are changing (related rates), first identify the quantity to be found, when it is to be found, and any other given values or rates.
The question asks for the rate of change in the angleθ when the drone's height h is 400 feet above point P. It is given that the person is 300 feet from point P, and the drone rises at a constant rate of feet per second.
A trigonometric equation for a right triangle that relates an acute angle θ of a right triangle to the lengths of the adjacent side b and opposite side h is
The angle θ and the length of the opposite side h are changing, but the adjacent side b remains constant. Plug the constant value b = 300 into the equation, differentiate with respect to time t,and solve for
| Equation for tangent of θ | |
| Plug in b = 300 | |
| Differentiate with respect to t | |
| Apply definition of secant | |
| Multiply both sides by cos 2θ |
The values of b and are given, and the trigonometric ratio for cos θ is However, the hypotenuse of the right triangle (the distance between the person and the drone) is unknown.
The height of the drone (400 feet) and the person's distance from point P (300 feet) correspond to a 3-4-5 Pythagorean triple, so the hypotenuse of the right triangle is 500 feet.
To find , substitute the values of b, , and cos θ into the equation for .
| Equation for with cos2 θ rewritten as (cos θ)2 | |
| Substitute values | |
| Simplify | |
| Multiply |
The rate of change of angle θ with respect to time t is radians per second.
(Choice B) may result from incorrectly differentiating tan θ as sec θ tan θ, instead of sec² θ.
(Choice C) may result from incorrectly differentiating tan θ as sin θ, instead of sec2 θ.
(Choice D) may result from incorrectly differentiating tan θ as cos² θ, instead of sec2 θ.
Things to remember:
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Question
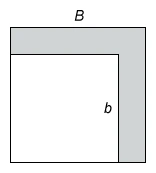
A region is bounded by two squares that have a common vertex at the bottom-left corner, as shown in the shaded region in the figure above. The side length of the outer square, B, is increasing at a constant rate of 3 meters per second, and the side length of the inner square, b, is decreasing at a constant rate of 1 meter per second. What is the rate of change, in square meters per second, of the area of the region at the instant when B is 5 meters and b is 4 meters?
| A. 4 | |
| B. 8 | |
| C. 22 | |
| D. 38 |
Hint :
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Explanation
To find a quantity when given the rates at which multiple variables are changing (related rates), first identify the quantity to be found, when it is to be found, and any other given values or rates.
The question asks for the rate of change in the shaded area when the side lengths B and b are 5 and 4 meters, respectively. Side length B is increasing and b is decreasing, so and meters per second.
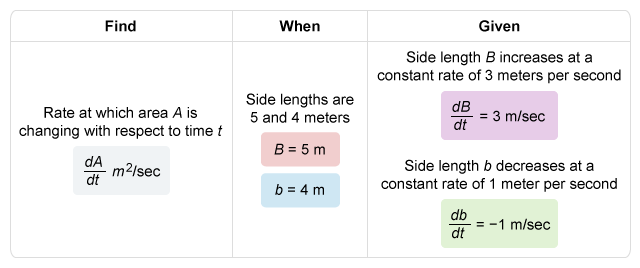
The area of the shaded region is given by the difference between the areas of the two squares. A square with side length s has area A = s2, so the shaded region has area A = B2 − b2.
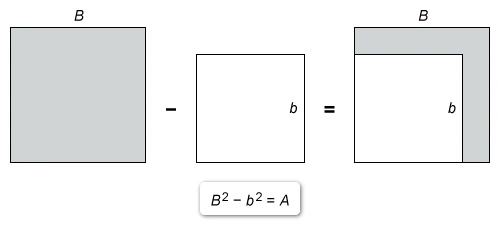
Now differentiate both sides of the equation with respect to t, plug in the given side lengths and rates of change, and evaluate
| Area of shaded region | |
| Differentiate with respect to t | |
| Plug in given values | |
| Simplify |
Therefore, the rate of change in the area of the shaded region at the given instant is 38 square meters per second.
(Choice A) 4 may result from the error described in Choice B and not including the constant multiple 2 when applying the power rule to differentiate (B − b)².
(Choice B) 8 may result from incorrectly using A = (B − b)² as the formula for the area of the shaded region, instead of A = B² − b².
(Choice C) 22 may result from incorrectly using as the rate of change for the smaller side length. The side length is decreasing, so the rate of change is negative.
Things to remember:
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.

Study On The Go
Stay exam-ready no matter where you are. Watch quick differentiation tutorials between classes, attempt Unit 4 AP Calc BC practice tests during commutes, or review optimization notes before bed. Every lesson, question, and guide syncs across devices, so your AP Calculus BC Unit 4 review is always organized and within reach.
Stand Out
with a Top Score on the AP Calculus BC Exam
Wrap up your AP Calc BC Unit 4 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
Which major topics fall under “Contextual Applications of Differentiation”?
AP Calculus BC Unit 4: Contextual Applications of Differentiation explores how derivatives describe change in physical and abstract systems. It’s where calculus meets real-world meaning. In this unit, you’ll learn how to connect derivative formulas with interpretation, using calculus to model, analyze, and predict change across motion, optimization, and growth problems.
The major topics include:
- Identifying relevant mathematical information in verbal representations of real-world problems involving rates of change
- Applying understandings of differentiation to problems involving motion
- Generalizing understandings of motion problems to other situations involving rates of change
- Solving related rates problems
- Local linearity and approximation
- L’Hospital’s rule
Each topic requires you to justify reasoning and communicate results clearly, the two skills that carry heavy weight in FRQs and MCQs on the AP Exam. UWorld’s AP Calculus Unit 4 review connects these abstract concepts to test-day logic with visuals, guided steps, and structured examples. By practicing with questions that mirror the AP style, you’ll develop fluency not only in problem-solving but also in writing mathematically sound explanations. This unit lays the groundwork for integration and motion in later units, making it a turning point in your AP Calculus BC preparation.
How does UWorld prepare me for the AP Calculus BC (Unit 4) exam?
UWorld prepares you for AP Calculus BC Unit 4 by strengthening conceptual control, analytical precision, and exam-oriented reasoning. The approach moves you from clear intuition to efficient execution without relying on mechanical memorization. The priority is your ability to interpret, justify, and communicate solutions in the format AP graders expect.
- Guided videos build intuition for motion, growth, related rates, and optimization, so each idea is understood before any procedure begins
- Interactive study guides connect equations, derivatives, graphs, and contextual meaning, tightening your recall and conceptual mapping
- AP-style practice sets expose you to real exam structure with full explanations that unpack each step, explain why it works, and clarify the final interpretation
- FRQ training forces disciplined communication by defining variables, justifying transitions, and framing answers within the problem’s context
- Timed quizzes replicate AP pacing and pressure to build fluency under constraints
Check for Understanding questions function as immediate progress audits after each subtopic. These items measure reasoning accuracy in real time and include explanations that model the precise calculus language used on the AP Exam. This structure sharpens memory, improves subtopic retention, and boosts performance on classroom progress checks. The same reasoning patterns extend directly to the official exam. The result is a preparation system that builds mastery through explanation, interpretation, and applied problem solving. UWorld positions you to handle Unit 4 MCQ and FRQ demands with clarity and to carry that mastery forward into the full AP Calculus BC exam.
Are there any free resources available for AP Calculus BC Unit 4?
Yes. Several high-quality resources can supplement your AP Calculus BC Unit 4 review, but UWorld’s free trial remains one of the most practical for focused, exam-style learning. It provides access to videos, practice questions, and rationales that mirror the format and difficulty of actual AP Exam problems. These materials help you preview the structure of UWorld’s full prep course and experience how its explanations guide your reasoning process. Beyond that, the College Board’s AP Classroom platform offers free topic outlines and sample Unit 4 AP Calc BC questions, which align with the core curriculum. However, these resources emphasize assessment rather than teaching. UWorld bridges that gap by combining instruction with active practice. Each question is accompanied by a detailed solution explaining both the calculus and the test-taking strategy behind it, something static resources can’t provide.
To maximize value, pair UWorld’s free materials with your class notes and official course framework. Watch one video per day, solve a few questions, and record mistakes in a short reflection log. That small, consistent routine helps strengthen weak areas while preparing you for deeper paid practice later. Even brief exposure to UWorld’s guided explanations can significantly improve conceptual clarity and test-day confidence.
What types of questions are on the AP Calculus BC Unit 4 test?
The AP Calculus BC Unit 4 test evaluates how well you can apply differentiation to solve real-world and abstract problems. It doesn’t focus on formula memorization but measures reasoning, justification, and interpretation. You’ll encounter both multiple-choice (MCQ) and free-response (FRQ) questions that require translating contextual information into calculus models.
The question types you’ll see include:
- Motion analysis: Finding velocity, acceleration, and distance using first and second derivatives.
- Related rates: Setting up and solving problems where multiple variables change together.
- Optimization: Determining maxima or minima for functions in real scenarios.
- Concavity and inflection: Using the second derivative to describe function behavior.
- Model interpretation: Explaining what a derivative means in context.
Each problem tests your ability to link symbolic manipulation to reasoning, which is exactly what UWorld’s AP Calculus BC Unit 4 review is built for. Every question in the platform mirrors AP Exam style, guiding you through setup, solution, and interpretation with clarity. The answer explanations also highlight typical AP scoring logic, helping you avoid subtle mistakes that cost points. By practicing these patterns repeatedly, you’ll move into the AP Exam able to identify question intent quickly and communicate complete, mathematically sound answers with confidence.
How much time should I spend reviewing AP Calculus BC Unit 4
AP Calculus BC Unit 4 demands spaced repetition because the exam tests interpretation of rates, motion, and optimization rather than formula recall. While 7 to 10 hours across 2 weeks is a reliable target for most students, you should focus on breaking the work into short sessions that cycle through relearning, applying, and analyzing. Revisit core differentiation ideas through concept videos until the meaning of a derivative in context is automatic. Move into targeted Unit 4 question sets and force yourself to read the full explanations even when your answer is correct. This exposes hidden reasoning gaps.
In the final stretch, switch to mixed timed quizzes that blend Unit 4 with adjacent areas. That shift builds the ability to interpret velocity, acceleration, and rate changes without stopping to rethink fundamentals. Stabilizing this unit strengthens performance across the entire course because AP Calc BC Unit 4 acts as the conceptual bridge from basic differentiation to the modeling ideas used later.
How can I improve my score on the FRQs and MCQs for Unit 4?
Raising your performance on AP Calc BC Unit 4 problems requires building a stable interpretation process for every derivative driven scenario. The exam measures your ability to read a situation, convert it into a mathematical structure, justify each step, and explain meaning in context. Strength in this unit comes from consistent reasoning, not shortcuts.
- Strengthen your first step. When you read an AP Calc BC Unit 4 prompt involving motion, identify position, velocity, and acceleration immediately. When you see quantities changing, identify the variables and the relationships that connect their rates. This front loaded clarity reduces hesitation and prevents setups that collapse later.
- Build a fixed structure for AP Calc BC FRQs. Define all variables at the start. Justify each algebraic move so the logic is visible. State what your final value represents in plain mathematical language. This structure aligns with the scoring rubric and removes ambiguity.
- Increase fluency by practicing AP Calc BC Unit 4 questions under time pressure. Use problems involving related rates, optimization, and motion interpretation until the setup becomes automatic. You want a process that remains stable even when the clock is tight.
After each practice session, isolate the source of every error. Most failures come from misreading the scenario, confusing variable relationships, or giving conclusions with no interpretation. Correct derivatives do not earn credit if the reasoning is unclear. Rebuild any concept that produces repeated mistakes. This method produces stronger interpretation, cleaner setups, sharper pacing, and more coherent explanations. Those improvements directly raise scores on AP Calc BC Unit 4 MCQs and AP Calc BC FRQs that test contextual applications of differentiation.
What is the "Contextual Applications of Differentiation" unit's weight on the AP Calculus BC exam?
AP Calculus BC Unit 4: Contextual Applications of Differentiation typically accounts for around 6-9% of the total exam score, depending on the year’s distribution. Although it appears early in the course, its influence extends across the entire exam because it connects directly to major concepts like motion, optimization, and growth modeling.
The unit’s weight lies not just in its percentage, but in its reach:
- Derivative interpretation underpins many questions from later units, including integration and motion analysis.
- Optimization and related rates form part of complex FRQs where multiple concepts overlap.
- Analytical reasoning developed here appears again in slope fields, parametric motion, and differential equations.
Mastering AP Calculus BC Unit 4 is essential for scoring high on the test. UWorld’s targeted review and practice simulate this integration by training you to approach problems with the same layered logic the exam demands. Even if only a fraction of questions belong explicitly to this unit, the reasoning patterns recur throughout the course. A strong grasp of Unit 4 can turn a borderline performance into a top-tier score.
Does UWorld let me review AP Calculus BC Unit 4 across multiple devices and continue studying offline?
Yes. UWorld’s platform makes AP Calculus BC Unit 4 review seamless across all devices, allowing you to learn anywhere and even access materials offline. You can start a session on your laptop, review explanations on your phone, and continue quizzes later on your tablet, and your data stays synced automatically. The UWorld app is built for students balancing busy schedules, enabling small, high-impact study bursts that still contribute to meaningful exam progress.
When you download the UWorld app, you can pre-load lessons and practice questions for offline use. This means that even without internet access, whether commuting, traveling, or studying in a low-connectivity area, you can continue practicing Unit 4 AP Calc BC questions uninterrupted. Once you reconnect, your progress, accuracy reports, and notes sync instantly across devices.
This flexibility is critical during exam season. Instead of waiting for long study windows, you can make steady progress in five- or ten-minute sessions, turning idle moments into productive learning time. Every question you review offline still provides the same detailed explanations, visuals, and reasoning found online. UWorld’s cross-platform design ensures that no matter where or how you study, you’re always building toward the same goal: mastering contextual differentiation for the AP Calculus BC Exam efficiently and consistently.
Where can I find a good study guide for AP Calculus BC Unit 4?
UWorld provides a fully interactive AP Calculus BC Unit 4 study guide crafted to match the College Board framework and the rigor of real exam questions. It goes beyond static notes, turning complex derivative applications into visual, step-by-step learning experiences that reinforce reasoning, not memorization.
Inside the guide you’ll find:
- Explanations linking motion graphs, slope analysis, and optimization models.
- Formula summaries organized by concepts, such as velocity, acceleration, related rates, and critical points.
- Worked examples with annotated solutions that show AP-style justification.
- Integrated “Check-for-Understanding” items that confirm mastery before advancing.
Unlike generic review sheets, UWorld’s guide mirrors the tone and format of exam reasoning, so you learn how to articulate calculus ideas precisely. Used alongside videos and practice test questions, it functions as both a teaching resource and a self-assessment tool. Every explanation connects derivative theory to exam-ready communication, thereby, training you to write concise, mathematically sound responses on test day.
Can I find practice tests specifically for AP Calc BC Unit 4?
Yes. UWorld offers AP Calculus BC Unit 4 practice tests created to match the complexity, structure, and pacing of the official AP Exam. Each set targets differentiation in context, such as motion, optimization, and related-rate scenarios with questions that reflect both multiple-choice logic and free-response rigor.
Every problem includes:
- Exam-style setup: Contextual wording identical to unit 4 ap calc bc prompts.
- Step-by-step solutions: Full rationales that explain not only how but why an answer is correct.
- Common-error analysis: Notes showing where students typically lose points and how to avoid them.
- Adaptive practice: Personalized question mixes that strengthen weak sub-topics before the exam.
Working through these sets builds automatic recognition of calculus patterns and helps you manage timing effectively. UWorld’s analytics track accuracy and improvement, turning practice data into actionable insight. By the time you reach the AP Exam, derivative applications, be it from velocity and acceleration to optimization, will feel familiar, logical, and completely within your control.
What are the most common mistakes students make on AP Calc BC Unit 4 questions?
Many students lose points in AP Calculus BC Unit 4 not because they lack knowledge, but because they misinterpret what derivatives represent in context. The most frequent mistake is treating differentiation mechanically rather than conceptually. Students often compute correct derivatives but fail to connect results to meaning, like explaining what a positive slope or zero acceleration indicates in a physical scenario.
Another recurring error is poor setup in related rate or optimization problems. A single missing variable relationship or incorrect assumption can derail the entire solution. Likewise, some skip labeling units, which costs clarity and sometimes points. Others over-rely on memorized formulas, ignoring whether conditions actually fit those models. To avoid these pitfalls, focus on interpretation first, calculation second. UWorld’s AP Calculus BC Unit 4 review materials emphasize understanding through visuals, step-by-step logic, and model reasoning. Each question includes complete justifications that illustrate how to translate numerical results into language that AP graders reward.
By training with these realistic exam-style questions, you’ll learn to identify traps instantly, organize work methodically, and express calculus ideas precisely. That shift from performing operations to explaining relationships is what separates a 3 from a 5.
What UWorld features are most useful for mastering AP Calculus BC Unit 4 concepts?
UWorld’s strength lies in how its tools transform AP Calculus BC Unit 4 from theory into an intuitive skill. The platform integrates several advanced learning features that guide you beyond rote calculation toward conceptual fluency, an essential shift for high-scoring AP students.
The most impactful features include Smart Flashcards, Performance Analytics, and Check-for-Understanding items. Flashcards allow you to instantly convert difficult practice questions into review notes, complete with solution explanations and visuals. You can tag these by topic, such as motion, optimization, or related rates, and revisit them in spaced intervals for retention. UWorld’s analytics, meanwhile, break your performance down by accuracy, topic strength, and time management, helping you pinpoint where comprehension gaps persist.
Another key feature is the interactive question explanation design: every problem contains diagrams, color cues, and reasoning chains that teach you how to think, not just how to compute. These make conceptual leaps like connecting slope, concavity, and change feel logical rather than abstract. By combining these tools in a steady study rhythm, you gain a 360-degree command of Unit 4 concepts and build the reasoning habits essential for both MCQs and FRQs.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Differentiation: Composite, Implicit, and Inverse Functions
Analytical Applications of Differentiation
Integration and Accumulation of Change
Differential Equations
Applications of Integration
Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Infinite Sequences and Series