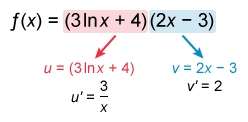AP® Calculus BC Unit 2 Review and Practice Test
If you’re preparing for AP® Calc BC Unit 2, this guide walks you through the essential ideas behind differentiation, from the formal definition to the most important derivative properties, you’ll use throughout the course. With step-by-step examples and exam-style questions, you’ll be able to practice strategically and track your progress as you work toward scoring high.
Boost Your Confidence and Score High with Our AP Calculus BC Unit 2 Review
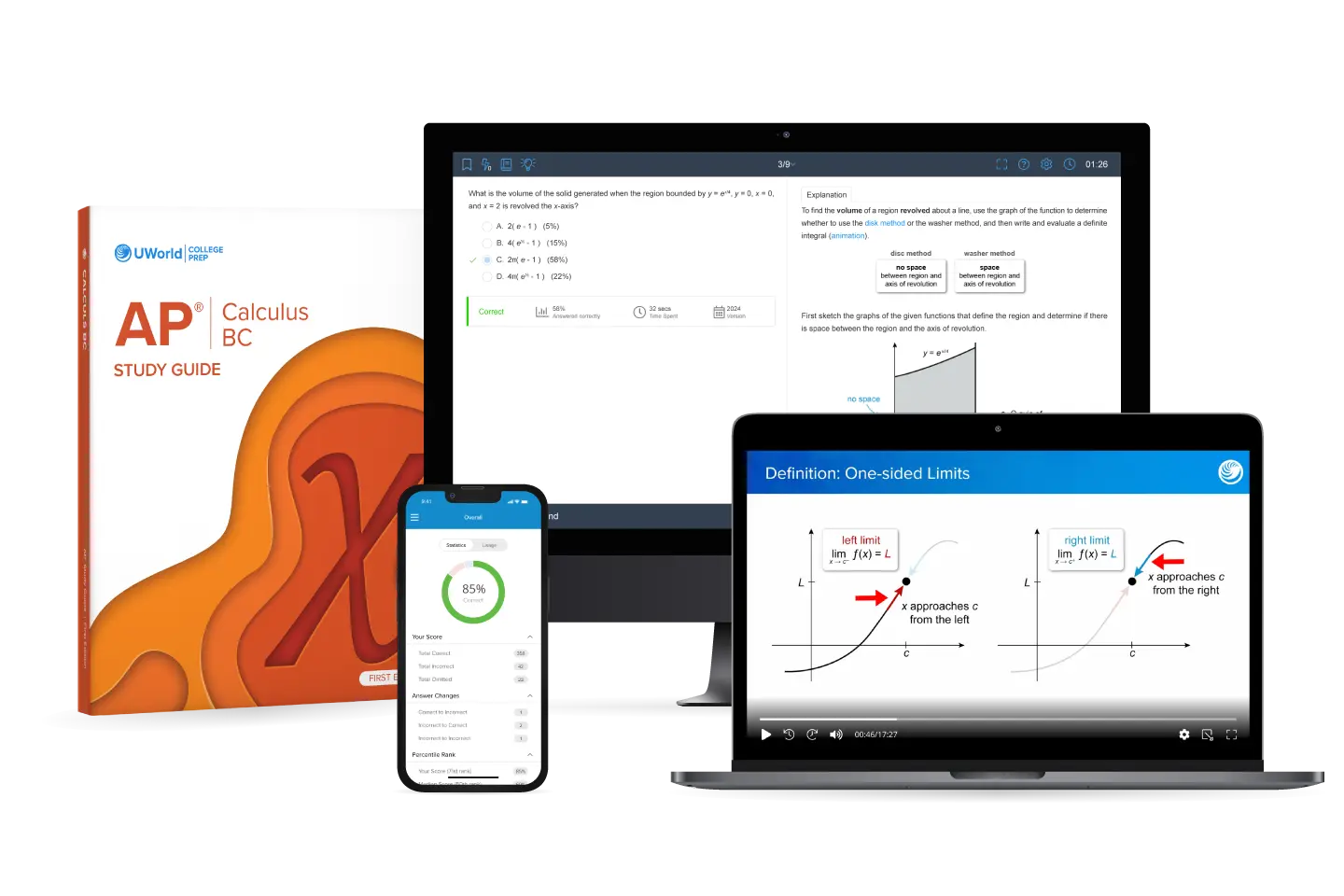
Get the support you need for a strong AP® Calculus BC Unit 2 review. Our expert-designed study materials break down limits, derivative definitions, and core rules into easy-to-follow lessons, helping you learn efficiently and build test-ready confidence.
Engaging Video Lessons
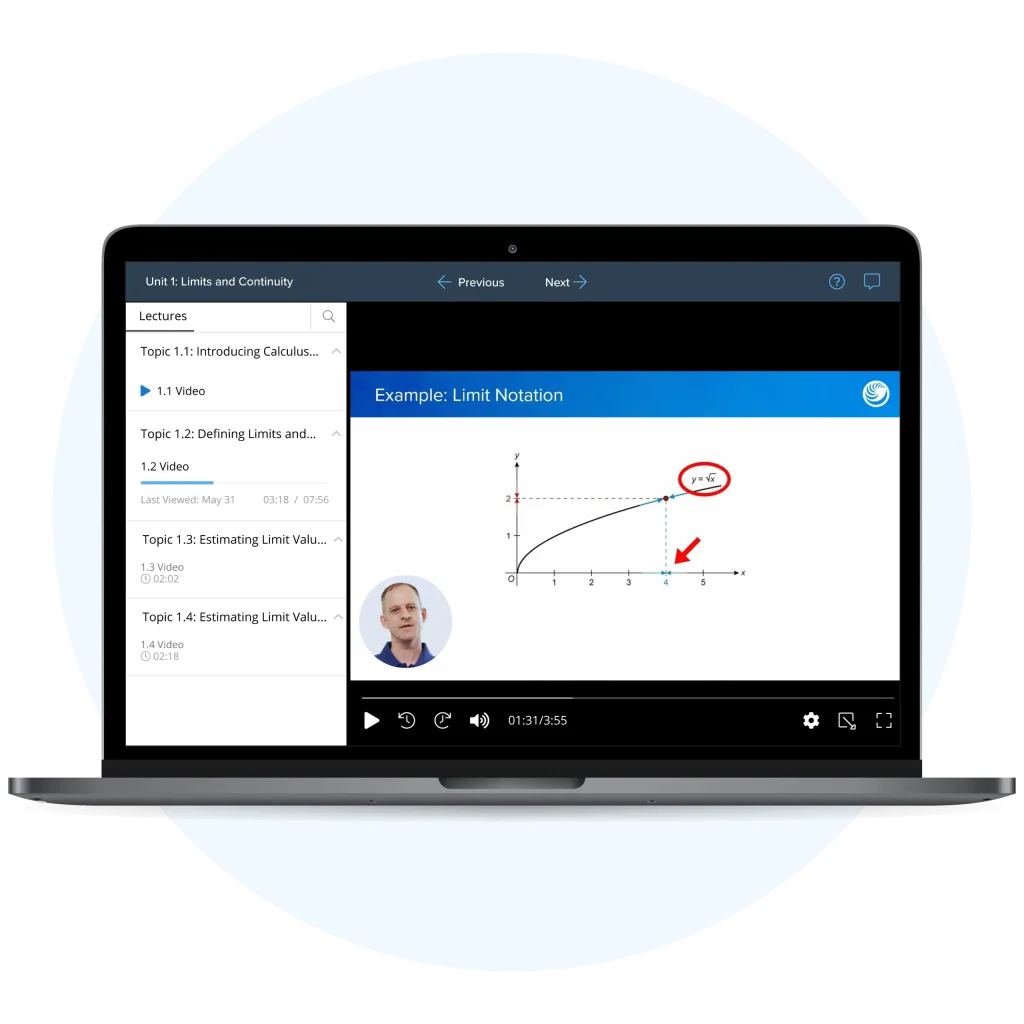
Stay focused and learn faster with our concise, engaging video lessons tailored for AP Calculus BC Unit 2. Instead of flipping through dense notes, you’ll get clear visual explanations that make differentiation concepts easier to understand and remember.
Interactive Study Guides
Our interactive guide for AP Calculus BC Unit 2 provides streamlined notes, clear visuals, and concept checkpoints that help you review efficiently. Everything is designed to match what you’ll see on test day, so your practice stays structured and effective.
Try These AP Calculus BC Unit 2 Practice Test Questions
Question
If f(x) = (3lnx + 4)(2x − 3), then f′(x) =
| A. | |
| B. | |
| C. | |
| D. |
Hint :
To find the derivative of the product of two functions, use the product rule.
Explanation
To find the derivative of the product of two functions, use the product rule:
First identify u and v from the given function f(x) = (3lnx + 4)(2x − 3), and then differentiate to determine u′ and v′.
(Choice A) may result from incorrectly calculating the derivative of the product as u′v′ instead of uv′ + vu′.
(Choice B) may result from incorrectly calculating the derivative of the product as u′ + v′ instead of uv′ + vu′.
(Choice D) may result from incorrectly calculating the derivative of the product as uu′ + vv′ instead of uv′ + vu′.
Things to remember:
To find the derivative of the product of two functions, use the product rule:
Question
If a function f is not differentiable at x = −2, which of the following statements must be true?
| A. f′(−2) = 0 | |
| B. f(−2) does not exist | |
| C.
does not exist |
|
| D.
does not exist |
Hint :
A function is differentiable at x = c only if its derivative at x = c exists.
Explanation
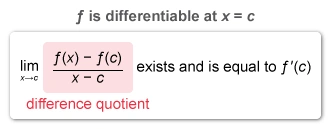
A function f is differentiable at x = c only if the derivative of f at x = c exists. If the derivative exists, then the limit of the difference quotient at x = c exists and is equal to the derivative.
Note: The limit of the difference quotient can also be expressed as
If f is not differentiable at x = −2, the derivative at x = −2 does not exist. Therefore, does not exist.
(Choice A) "f′(−2) = 0" may result from the misconception that if a function is not differentiable at a point, then its derivative is zero at that point instead of nonexistent.
(Choice B) "f(−2) does not exist" may result from assuming that if a function is not differentiable at a point, then the function does not exist at that point.
(Choice C) "does not exist" may result from mistaking the limit of f as x approaches −2 with the limit of the difference quotient as x approaches −2.
Things to remember:
A function f is differentiable at x = c if the derivative of f at x = c exists. If the derivative exists, the limit of the difference quotient
exists and is equal to the derivative f′(c).
Question
The oil temperature in a car's engine is modeled by T, where T(t) is the temperature in degrees Fahrenheit, and t is the time, in minutes, after the engine is started. Which of the following indicates that the oil is getting hotter 12 minutes after the engine is started?
| A. T(12) < 0 | |
| B. T(12) > 0 | |
| C. | |
| D. |
Hint :
The sign of the derivative of a function indicates whether the function is increasing or decreasing.
Explanation
The function T gives the temperature of the oil in the car's engine, so the derivative of T gives the instantaneous rate of change in the temperature of the oil.
The sign of T′ indicates whether the temperature T of the oil is increasing or decreasing. If the values of the function's derivative T′ are positive, then the values of T are increasing.
If the oil is getting hotter 12 minutes after the engine is started (at t = 0), the temperature of the oil is increasing at t = 12. Therefore, the derivative of T is positive at that time:
(Choice A) T(12) < 0 indicates that the temperature of the oil is negative at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
(Choice B) T(12) > 0 indicates that the temperature of the oil is positive at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
(Choice C) indicates that the temperature of the oil is getting cooler at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
Things to remember:
- The notation gives the derivative of a function y with respect to x.
- If the derivative of a function is positive, then y is increasing. If is negative, then y is decreasing.
Stand Out
with a Top Score on the AP Calculus BC Exam
Wrap up your AP Calc BC Unit 2 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What is AP Calculus BC Unit 2 and why is it important for the exam?
AP Calculus BC Unit 2 focuses on the definition and fundamental properties of derivatives, forming the base for nearly every major topic you’ll encounter later in the course. Many AP FRQs and MCQs, including AP Calculus BC Unit 2 progress check MCQ part A and AP Calculus BC Unit 2 progress check MCQ part B, directly test these skills, which makes developing a strong understanding of this unit essential for scoring well. A consistent AP Calc BC Unit 2 review also prepares you for applied concepts in Units 3, 4, and 5.
To study Unit 2 effectively, focus on:
- Understanding the derivative definition using limits and continuity.
- Practicing core rules (Power, Product, Quotient, Chain Rule).
- Analyzing graphs of fff, f′f’f′, and f′′f”f′′ to explain behavior and motion.
- Completing Unit 2 AP Calc BC progress-check sets to identify conceptual gaps.
- Using FRQ-style reasoning similar to what appears in AP Calc BC Unit 2 FRQ problems.
Building a solid conceptual foundation in Unit 2 allows you to approach later topics, including integration and series, with confidence. Regular practice with MCQs, FRQs, and timed exercises helps ensure both speed and accuracy on the AP Calculus BC exam.
Which topics are covered in AP Calculus BC Unit 2?
AP Calculus BC Unit 2 focuses on the definition and fundamental properties of derivatives, including rules for differentiation, continuity, and instantaneous rate of change. Key concepts appear repeatedly in AP Calculus BC Unit 2 progress check MCQ part A and part B, and AP Calc Unit 2 FRQs.
Major topics include:
- Derivative definition & rate of change: Average vs. instantaneous change.
- Continuity & differentiability: When derivatives exist.
- Core derivative rules: Power, sum/difference, constant multiple.
- Product & Quotient Rules: Essential for more complex functions.
- Trig & transcendental derivatives: sin, cos, e^x, ln(x).
UWorld’s AP Calculus BC Unit 2 resources guide you through each topic with step-by-step visuals, relevant examples, and practice questions. When combined with progress-check MCQs and classroom resources, they reinforce understanding, strengthen procedural fluency, and improve time-management for test day.
How should I study for the AP Calculus BC Unit 2 review?
A strong AP Calculus BC Unit 2 review focuses on understanding derivative definitions, mastering differentiation rules, and applying concepts to real problems. Working through the AP Calculus BC Unit 2 progress check MCQ Part A and Part B, along with AP Calculus BC Unit 2 FRQs, helps you build the skills needed for the exam. Early prep with AP Calculus BC Unit 2 practice test questions also boosts confidence and reduces errors on both MCQs and FRQs.
Study plan:
- Week 1: Understand the derivative as a limit and explore continuity and differentiability.
- Week 2: Practice core rules: Power, Sum/Difference, Product, and Quotient Rules.
- Week 3: Apply trig and exponential/log derivatives in computation and real-world problems.
- Final review: Complete mixed MCQs and FRQs, and revisit errors from Unit 2 AP Calculus BC review progress checks.
This structured study approach ensures that you not only memorize formulas but also understand their applications, improving your performance in timed exams and providing a strong foundation for subsequent AP Calculus BC units.
What’s the best study sequence for AP Calculus BC Unit 2?
For AP Calculus BC Unit 2, following a logical progression ensures mastery of derivative definitions, fundamental rules, and practical applications before attempting mixed exercises or timed tests.
Recommended sequence:
- Start with derivative definition & rate of change: Focus on limits, continuity, and instantaneous change.
- Core derivative rules: Master Power, Sum/Difference, Product, Quotient, and Chain Rules.
- Trig and transcendental derivatives: Learn derivatives of sin, cos, e^x, ln(x), etc.
- Applied problems: Solve motion, optimization, and related-rate exercises.
- Final review: Integrate all topics with mixed Unit 2 AP Calc BC exercises and timed practice tests.
Following this sequence ensures a strong conceptual foundation and smooth transition to more complex applications in later units. Consistent, stepwise practice builds confidence, reduces errors, and improves speed, preparing you to tackle both Unit 2 assessments and cumulative AP Calculus BC exam questions effectively.
What is the most effective AP Calculus BC Unit 2 review plan before the exam?
A well-structured AP Calc BC Unit 2 review builds understanding gradually while reinforcing problem-solving skills. Focusing on AP Calculus BC Unit 2 FRQs and AP Calc BC Unit 2 practice test questions for MCQ section ensures both conceptual mastery and exam readiness.
Suggested review timeline:
- 3 months before the exam: Review derivative definitions, limits, and continuity; watch short lessons on basic derivative rules; solve small practice problems to apply concepts.
- 1 month before the exam: Focus on Product, Quotient, and Chain Rules; practice trig and exponential/log derivatives; attempt AP Calc BC Unit 2 practice test weekly to check progress; create formula summaries and notes. UWorld’s AP Calculus BC Unit 2 lessons and practice sets provide step-by-step examples and interactive exercises that mirror real exam questions, helping you track progress effectively.
- 2 weeks before the exam: Work through mixed MCQs and FRQs, including applied rate-of-change problems; review errors, focus on interpretation, and refine pacing for exam conditions.
This timeline ensures steady progress, reinforces both computation and reasoning, and builds confidence in applying AP Calculus BC Unit 2 concepts under timed conditions. Consistent practice prepares students to tackle all Unit 2 topics efficiently on test day.
What are the main FRQ question types for AP Calculus BC Unit 2?
AP Calculus BC Unit 2 FRQs focus on derivative definitions, differentiability, and fundamental rules. Mastering these concepts through a targeted AP Calculus BC Unit 2 review helps you handle both computation and reasoning questions efficiently.
Common FRQ types include:
- Definition & interpretation tasks: Define the derivative or explain differentiability at a point.
- Rate-of-change/tangent-line problems: Use limits or derivatives to find slopes and interpret context.
- Derivative-rule application: Apply Power, Sum/Difference, Product, Quotient, and trig/exponential derivatives.
- Graph/continuity/differentiability questions: Determine where f′ exists and interpret slopes from graphs or tables.
- Mixed format: Combine computation with interpretation in multi-part questions.
Focus on FRQs that pair calculations with explanations to reinforce understanding. Practicing these consistently as part of your AP Calc BC Unit 2 review will strengthen both procedural skills and conceptual reasoning for the exam.
How can I use UWorld to improve my AP Calculus BC Unit 2 MCQ scores?
UWorld is designed to help students master AP Calc BC Unit 2 concepts through practice that mirrors the real exam. Using UWorld’s Unit 2 lessons, MCQs, and practice tests allows you to identify weak areas in derivative definitions, differentiability, and core derivative rules while reinforcing problem-solving skills.
Strategies to improve with UWorld:
- Timed practice sets: Complete UWorld’s MCQs to simulate exam conditions and build speed.
- Step-by-step solutions: Review detailed explanations to understand why each answer is correct or incorrect.
- Mix in FRQs: Apply derivative concepts to UWorld’s AP Calc BC Unit 2 FRQ questions to connect computation with reasoning.
- Track performance: Use UWorld’s progress analytics to focus on topics that need more practice.
How are derivative concepts connected in AP Calculus BC Unit 2?
Understanding how derivative concepts link together is essential for mastering AP Calculus BC Unit 2. The derivative definition forms the foundation, explaining rates of change and the slope of tangent lines. From there, the basic derivative rules, such as Power, Sum/Difference, Product, Quotient, and Chain Rules, allow you to compute derivatives efficiently.
Key connections:
- Definition → Rules: Knowing what a derivative represents helps you understand why the rules work.
- Derivative → Application: Apply derivatives to motion, optimization, and related-rate problems.
- Interpretation → Analysis: Use derivatives to analyze function behavior, such as increasing/decreasing intervals or local extrema.
By seeing these concepts as interconnected rather than isolated, you can approach Unit 2 AP Calc BC FRQs and MCQs with a deeper understanding, making problem-solving faster, more accurate, and more intuitive.
How can I retain formulas and key concepts from AP Calculus BC Unit 2?
Retention in AP Calculus BC Unit 2 relies on connecting formulas with their conceptual meaning. Simply memorizing rules isn’t enough; understanding why each derivative formula works helps you recall and apply them under exam conditions.
Strategies for better retention:
- Create a formula sheet: Include Power, Sum/Difference, Product, Quotient, and Chain Rules, along with derivatives of trig, exponential, and logarithmic functions.
- Use visual aids: Sketch tangent lines, slopes, or small graphs to link formulas to their geometric interpretation.
- Practice in context: Solve AP Calc BC Unit 2 FRQ and practice test problems applying each formula to real-world situations.
- Active recall with flashcards: Use UWorld’s AP Calculus BC formula sheets and digital flashcards to reinforce key rules and test yourself regularly.
Combining these approaches ensures that you don’t just memorize but deeply understand Unit 2 AP Calc BC formulas and concepts. Structured practice with UWorld’s tools improves both speed and accuracy, giving you confidence on MCQs and FRQs.
How do I study derivative analysis effectively for the AP Calculus BC Unit 2 test?
Studying derivative analysis in AP Calculus BC Unit 2 requires balancing conceptual understanding, computation, and interpretation. You need to connect derivative definitions, rules, and applications to solve MCQs and FRQs efficiently.
Effective strategies:
- Focus on core derivatives: Review Power, Sum/Difference, Product, Quotient, and Chain Rules, as well as trig, exponential, and logarithmic derivatives.
- Apply to real problems: Practice AP Calc BC Unit 2 FRQs that involve rates of change, tangent lines, and function analysis.
- Visualize and interpret: Draw graphs and slopes to understand how derivatives describe increasing/decreasing behavior, concavity, and extrema.
- Timed practice: Simulate exam conditions to improve speed and accuracy.
- Use UWorld tools: Leverage UWorld’s Unit 2 lessons, practice sets, and formula sheets for interactive problem-solving and step-by-step explanations.
By combining conceptual review, applied exercises, and guided practice with UWorld, you can strengthen both computation and reasoning skills, ensuring confidence and efficiency on the AP Calculus BC Unit 2 test.
What is the best AP Calculus BC Unit 2 practice-test format?
An effective AP Calc BC Unit 2 practice test balances multiple-choice and free-response questions to reflect the real exam. Focusing on both computation and interpretation ensures you are prepared for all question types.
Recommended format:
- MCQs: 25–30 questions covering derivative definitions, Power/Chain/Product/Quotient Rules, and applied rate-of-change problems.
- FRQs: 1–2 multi-part questions involving derivative computation, tangent lines, function analysis, and interpretation of slopes.
- Timing: 60–70 minutes total to simulate real exam pacing and reinforce time management skills.
- Review: Analyze mistakes to identify conceptual gaps versus procedural errors.
Practice with UWorld’s AP Calculus BC Unit 2 tests and explanations to simulate the real exam experience. Interactive feedback and detailed explanations help reinforce reasoning, clarify misunderstandings, and improve speed, accuracy, and confidence for the actual test.
When should I begin preparing for the AP Calculus BC Unit 2 test?
You should begin reviewing AP Calculus BC Unit 2 as soon as derivative concepts are introduced in class. Early preparation helps build a solid foundation in derivative definitions, differentiability, and derivative rules, which appear in both MCQs and FRQs.
Recommended timeline:
- 3–4 weeks before the test: Review basic derivative definitions, limits, and continuity; practice small computation problems.
- 2 weeks before the test: Focus on applying derivative rules (Power, Product, Quotient, Chain) and solve AP Calc BC Unit 2 practice test questions.
- Final week: Work through mixed MCQs and FRQs under timed conditions, emphasizing interpretation and error analysis.
Consistent short sessions (20–30 minutes daily) improve retention better than infrequent long sessions. Incorporating UWorld’s Unit 2 lessons, MCQs, and formula sheets can reinforce concepts, track progress, and build confidence for the exam.
What are the common mistakes students make in AP Calculus BC Unit 2?
In AP Calculus BC Unit 2, students often lose points on MCQs and FRQs because of small misunderstandings about derivatives.
Frequent mistakes include:
- Confusing differentiability with continuity, assuming a function is differentiable just because it’s continuous.
- Misapplying derivative rules, especially Product, Quotient, and Chain Rules.
- Forgetting to interpret slopes or rates of change in context on FRQs.
- Errors in limit calculations when defining derivatives from first principles.
- Overlooking the significance of points where derivatives do not exist.
To avoid these pitfalls, review errors from AP Calc BC Unit 2 progress-check MCQs and practice tests, and reinforce understanding with UWorld’s Unit 2 lessons, interactive explanations, and formula sheets. Consistent review and targeted practice help prevent these errors and improve both accuracy and confidence on exam day.
Where can I find AP Calculus BC Unit 2 notes, cheat sheets, or study guides?
High-quality AP Calculus BC Unit 2 study materials summarize essential concepts such as derivative definitions, differentiability, and core derivative rules. These resources help you review efficiently and reinforce understanding for both MCQs and FRQs.
Best options include:
- Comprehensive notes: Step-by-step explanations of derivative rules, examples, and applications.
- Cheat sheets: Quick-reference guides for formulas, derivative rules, and common problem types.
- Study guides: Structured review materials with visual aids, practice problems, and solved examples.
- UWorld resources: UWorld offers Unit 2 formula sheets, interactive flashcards, and guided lessons that mirror College Board® expectations, making it easy to reinforce concepts and track mastery.
Using a combination of concise cheat sheets, detailed notes, and UWorld’s interactive tools ensures you retain critical Unit 2 AP Calc BC concepts and are well-prepared for exam questions.
Are there downloadable AP Calculus BC Unit 2 study-guide PDFs and practice materials?
Yes, students can use College Board materials to review AP Calculus BC Unit 2 efficiently. The College Board provides official PDFs, sample MCQs, and FRQs that reflect the exact format, content, and level of difficulty found on the exam. These resources summarize key derivative rules, formulas, and problem types, allowing students to practice in a structured, exam-focused way and understand how the test assesses both computation and reasoning skills.
Additionally, UWorld offers Unit 2 study PDFs, interactive flashcards, and practice sets that provide step-by-step solutions and problem-solving strategies. Using these alongside official College Board resources ensures comprehensive preparation for Unit 2 AP Calc BC, strengthens conceptual understanding, and builds confidence for both MCQs and FRQs.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Differential Equations
Applications of Integration
Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Infinite Sequences and Series