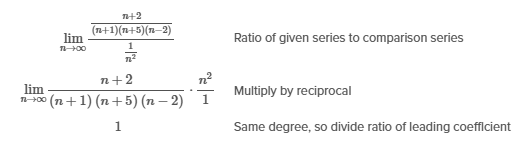AP® Calculus BC Unit 10 Review and Practice Test
Get ready for your Unit 10 AP® Calculus BC test with our comprehensive Infinite Sequences and Series review. This unit dives into convergence and divergence of series, Taylor and Maclaurin expansions, and power series applications, key topics that define success in advanced calculus. Our AP Calculus BC Unit 10 study guide includes exam-style MCQs, FRQs, and practice tests that reflect real AP exam expectations. Whether you’re reviewing formulas, solving step-by-step problems, or watching quick concept videos, this guide helps you master sequences and series with confidence before test day.
Boost Your Confidence and Score High with Our AP Calculus BC Unit 10 Review
Build the skills you need to excel on the AP Calculus BC Unit 10 test with focused lessons on infinite sequences and series. This unit challenges students to apply advanced calculus reasoning to analyze series convergence, Taylor series, and Maclaurin approximations. Our AP Calc BC Unit 10 review simplifies these complex ideas through structured lessons, clear visuals, and targeted practice questions designed to improve accuracy and confidence for both MCQs and FRQs.
Engaging Video Lessons
Challenging topics like infinite series convergence, Taylor and Maclaurin expansions, and radius of convergence are explained through short, engaging videos that simplify complex steps into clear visual logic. Each lesson focuses on understanding patterns, applying convergence tests, and connecting formulas to real AP exam questions. Learn faster and retain more with concise, high-yield videos crafted for the AP Calculus BC Unit 10 review experience.
Interactive Study Guides
Explore the AP Calculus BC Unit 10 study guide to master every concept in infinite sequences and series; from identifying convergence and divergence to working with Taylor polynomials and power series. Each topic is presented with clear definitions, solved examples, and formula breakdowns for quick recall. Visual aids and stepwise problem-solving methods make abstract ideas intuitive and practical for both MCQs and FRQs.
Try These AP Calculus BC Unit 10 Practice Test Questions
Question
If the first term of a geometric series is , which of the following series converges to ?
| A. | |
| B. | |
| C. | |
| D. |
The value to which a geometric series converges is equal to the sum of the geometric series.
Explanation
A geometric series is of the form , where a is a constant and r is the common ratio.
The value to which a geometric series converges is equal to the sum of the geometric series, where S is the sum, a1 is the first term, and r is the common ratio.
To determine which series has a first term a1 of and a sum of (converges to) , first calculate the common ratio. Plug the values of a1 and S into the formula above and solve for r.
| Sum of a geometric series formula | |
| Plug in and | |
| Multiply both sides by -1 | |
| Multiply both sides by common denominator 4(1-r) | |
| Simplify | |
| Subtract 1 from both sides and multiply both sides by -1 |
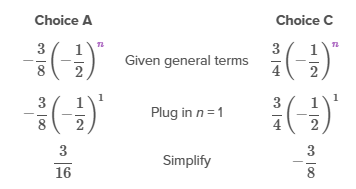
The common ratio is , so the series will be of the form . Eliminate Choices B and D because they do not have a common ratio of .
Now plug n = 1 into arn for the remaining two series to see which has a first term of .
Therefore, the series that converges to with a first term of is .
(Choice A) may result from assuming that a in the general series is equal to the first term a1, but a from the general formula is a different constant because the series starts at n = 1.
(Choice B) converges to , but the first term is instead of .
(Choice D) has a first term of , but converges to instead of .
Things to remember:
- A geometric series is of the form , where r is the common ratio.
- The value to which a geometric series converges is equal to the sum of the geometric series, where S is the sum, a1 is the first term, and r is the common ratio.
Question
Which of the following series converge?
| I. | II. | III. |
| A. I only | |
| B. II only | |
| C. II and III only | |
| D. I, II, and III |
If the general term an of a series includes an n in a factorial or an exponent, the ratio test may be used to determine its convergence.
Explanation
To determine the convergence of the given series, first determine which convergence test should be used.
Series I and II
The first two given series contain n in a factorial, so use the ratio test to determine their convergence. Evaluate for each series and determine whether the result is less than 1.
Find an+1 for each series (calculations). Then substitute the expressions for an and an+1 into the ratio test limit for both series, and compare the degrees to evaluate the resulting limits.
| Series I | Series II | |
|---|---|---|
|
Limit from ratio test |
||
|
Substitute expressions for an and an+1 |
||
|
Simplify and substitute simplified expressions for |
||
|
Evaluate limits |
Series I diverges because and Series II converges because 0 < 1. It is possible to eliminate Choices A and D because they include Series I.
Series III
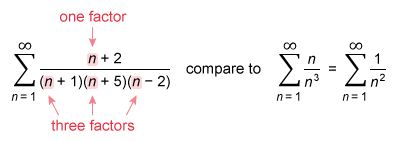
The third series is a rational expression with a higher degree in the denominator, so use the limit comparison test and compare the series with an appropriate p-series to determine its convergence.
To choose a p-series for comparison, disregard all but the number of factors of n in both the numerator and denominator of the given rational series. Simplify the result, if possible.
The comparison series is a p-series with p = 2, so it converges. Apply the limit comparison test , where and . Then compare the growth rates of the individual terms.
The limit is positive and finite and converges, so Series III converges. It is possible to eliminate Choices A and B because they do not include Series III.
Therefore, only Series II and III converge.
Things to remember:
-
If the general term an of a series includes an n in a factorial or an exponent, use the ratio test to determine its convergence.
-
Use the limit comparison test to determine the convergence or divergence of an infinite series that closely resembles a p-series by comparing the series to a simpler function.
Question
Which of the following series are absolutely convergent?
| A. II only | |
| B. III only | |
| C. I and II only | |
| D. I and III only |
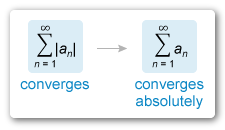
A series is absolutely convergent if converges.
Explanation
A series is absolutely convergent if converges.
To determine which of the given series converges absolutely, first find the absolute value of an for each series. For positive integer values of n, |(−1)n| = 1 and the value of each resulting fraction is positive.
Now choose an appropriate convergence test to determine whether each series converges or diverges.
Series I
The resulting series is the harmonic series, which diverges. The series diverges, so Series I does not converge absolutely. Therefore, it is possible to eliminate Choices C and D because they include Series I.
Series II
Apply the nth term test and compare the rates of growth to determine the convergence of the resulting series.
The limit is infinite, so the series diverges and Series II does not converge absolutely. Therefore, it is possible to eliminate Choices A and C because they include Series II.
Series III
Use exponent rules to rewrite the resulting series in the general form of a geometric series (calculation) and identify the value of the common ratio r.
The series is geometric, with a common ratio of . Therefore, the series converges since |r| < 1. Series III converges absolutely, so it is possible to eliminate Choices A and C because they do not include Series III.
Therefore, the series that is absolutely convergent is III only.
Things to remember:
A series
is absolutely convergent if
converges.

Study Anywhere, Anytime
Make your AP Calculus BC Unit 10 review fit your schedule. Solve infinite series practice questions during your commute, revisit Taylor and Maclaurin series lessons between classes, or read through your Unit 10 study guide at the café. With UWorld’s mobile-friendly platform, you can watch videos, take notes, and practice MCQs wherever you are, helping you stay consistent and confident.
Stand Out
with a Top Score on the AP Calculus BC Exam
Complete your AP Calculus BC Unit 10 review and continue mastering every unit to boost your overall performance. Consistent practice and conceptual clarity will set you apart as a standout candidate for competitive colleges and scholarships.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What is AP Calculus BC Unit 10 and why is it important for the exam?
AP Calculus BC Unit 10, titled Infinite Sequences and Series, is one of the most conceptually demanding sections of the course. It explores how infinite processes can produce finite results, an essential idea for higher-level calculus. Topics include sequence convergence, series convergence tests, and Taylor and Maclaurin series, all of which appear frequently on both AP Calc BC Unit 10 FRQs and MCQs.
Understanding Unit 10 is key because it builds directly on earlier concepts from limits and derivatives, applying them to infinite sums and approximations. Many AP Calculus BC Unit 10 practice test questions test your ability to decide whether a series converges and to use power series to represent functions.
To study effectively:
- Start with convergence tests (geometric, p-series, ratio, and alternating).
- Move to power and Taylor series expansions.
- Practice writing and interpreting Maclaurin polynomials.
Unit 10 deepens mathematical reasoning by connecting patterns, functions, and limits, a skill set vital for top scores on the AP Calculus BC exam.
What topics are covered in Unit 10 AP Calculus BC?
Unit 10 of AP Calculus BC, titled Infinite Sequences and Series, explores how infinite mathematical processes can lead to finite, meaningful results. These concepts are key to advanced calculus and appear frequently on AP Calc BC Unit 10 MCQs and FRQs. Understanding this unit is crucial for solving problems involving series convergence, approximation, and Taylor expansions.
Key topics in the AP Calculus BC Unit 10 review include:
- Sequences and Limits: Determining convergence or divergence using limit definitions.
- Infinite Series: Understanding partial sums and the meaning of convergence.
- Convergence Tests: Geometric, p-series, ratio, root, and alternating series tests.
- Power Series: Expressing functions as infinite polynomials within intervals of convergence.
- Taylor and Maclaurin Series: Constructing function approximations and estimating remainders.
- Applications: Using series for function modeling, error estimation, and real-world problems.
Once you review each topic, reinforce your understanding through AP Calculus BC Unit 10 progress check practice sets and Unit 10 AP Calc BC practice tests. These help identify gaps, improve conceptual clarity, and prepare you for exam-style reasoning. Building mastery across these areas ensures a strong foundation for tackling both theoretical and applied questions in Unit 10 AP Calculus BC and beyond.
How should I study for the AP Calculus BC Unit 10 review?
Preparing for AP Calculus BC Unit 10 requires both conceptual understanding and steady practice with convergence tests, series manipulations, and function approximations. Since this unit extends limits and derivatives into infinite processes, it’s one of the most analytical topics covered in AP Calc BC Unit 10 review lessons and exams.
To study effectively:
- Start with theory: Review definitions of sequences, limits, and convergence using your AP Calc BC Unit 10 study guide.
- Learn the tests methodically: Master geometric, ratio, root, and alternating series tests through guided examples.
- Practice pattern recognition: Identify which convergence test applies to a given series type.
- Apply real-world examples: Connect Taylor and Maclaurin series to function approximations and error analysis.
- Test retention regularly: Use short Unit 10 AP Calculus BC practice tests to check your understanding of infinite series and convergence behavior.
Incorporating structured practice through progress check-style sets helps you assess comprehension and accuracy after each concept. Reviewing feedback from your attempts allows you to pinpoint weak areas and build confidence for the AP Calc BC Unit 10 test.
By combining stepwise learning, consistent practice, and timed review sessions, you’ll develop the reasoning skills needed to handle both conceptual and computational questions on the AP Calculus BC Unit 10 exam.
What’s the best study sequence for AP Calculus BC Unit 10?
A well-structured study sequence for AP Calculus BC Unit 10 helps you progress from fundamental definitions to complex applications like Taylor and Maclaurin series. Since Unit 10 involves multi-layered reasoning, following a logical order ensures you fully grasp the relationships between sequences, series, and convergence behavior before attempting the more advanced polynomial approximations tested on AP Calc BC Unit 10 FRQs and MCQs.
Recommended sequence for your AP Calc BC Unit 10 review:
- Begin with sequences: Understand how to determine convergence using limit definitions.
- Explore infinite series: Learn about geometric and p-series to build the foundation for more advanced tests.
- Study convergence tests: Focus on ratio, root, and alternating series tests, identifying when each applies.
- Move to power series: Practice expanding functions into series and identifying intervals of convergence.
- Finish with Taylor and Maclaurin series: Learn how to approximate functions and estimate remainders.
As you move through each section, take mini Unit 10 AP Calculus BC practice tests or checkpoint quizzes to reinforce learning. Integrating brief review sessions after each topic solidifies retention and prepares you for mixed-topic questions that often appear in the AP Calc BC Unit 10 test. This layered approach ensures conceptual clarity and strong performance on the final exam.
What is the most effective AP Calculus BC Unit 10 review plan before the exam?
To prepare efficiently for AP Calculus BC Unit 10, it’s best to follow a time-based plan that combines theory, problem-solving, and timed review. Infinite sequences and series require repeated exposure, so organizing your review over several weeks will ensure a deep understanding of convergence tests and Taylor/Maclaurin expansions before test day.
3 Months Before the Exam:
- Review sequence and series basics from Units 8 and 9 to strengthen foundational understanding.
- Study convergence tests in detail; geometric, ratio, and alternating series are especially common in AP Calc BC Unit 10 FRQs.
- Watch short review videos and take structured notes from the How to Study for AP Calculus BC guide to pace your learning.
1 Month Before the Exam:
- Practice Unit 10 AP Calculus BC MCQs and written problems involving power and Taylor series.
- Focus on error estimation, radius of convergence, and remainder terms.
- Start short AP Calculus BC Unit 10 practice tests to build familiarity with exam-style phrasing.
2 Weeks Before the Exam:
- Attempt timed FRQs and mixed-series sets that combine convergence, partial sums, and function approximation.
- Review your notes and formula sheet daily.
- Revisit difficult convergence problems through practice sets for mastery.
A consistent, layered approach helps you retain the logic behind each test and apply it flexibly during your AP Calc BC Unit 10 test.
What are the main FRQ question types for AP Calculus BC Unit 10?
The AP Calculus BC Unit 10 FRQs test how well you understand the logic and application of infinite sequences and series. These questions often require students to justify convergence, find remainders, or use Taylor and Maclaurin series to approximate function values. Unit 10 problems are concept-heavy, so showing clear reasoning is as important as getting the final answer.
Common FRQ question types include:
- Convergence and Divergence Proofs: Explaining why a given series converges using tests such as the Ratio or Alternating Series Test.
- Taylor and Maclaurin Series Applications: Deriving and using polynomial approximations to estimate function values.
- Error Estimation and Remainder Analysis: Using Lagrange’s error bound to discuss approximation accuracy.
- Interval of Convergence: Determining where a power series converges or diverges.
- Connections to Prior Units: Applying derivatives and integrals when building series representations of functions.
When practicing Unit 10 AP Calc BC FRQs, focus on clarity in explanation, correct notation, and justification for each conclusion. Many scoring points come from reasoning rather than computation. Reviewing examples from past FRQs and practicing question types found in AP Calculus BC Unit 10 practice tests helps you strengthen accuracy and timing for the exam.
How can I improve my accuracy on AP Calculus BC Unit 10 MCQs and practice questions?
Improving accuracy on AP Calculus BC Unit 10 MCQs comes down to understanding convergence logic and avoiding common conceptual traps. This unit challenges students to distinguish between convergence tests, identify interval boundaries, and interpret function approximations correctly; all skills tested frequently in AP Calc BC Unit 10 practice questions and progress check-style reviews.
Here’s how to build precision and consistency:
- Identify keywords in each problem: Look for cues like “absolute convergence,” “radius of convergence,” or “alternating series,” which hint at the correct test to apply.
- Review formulas frequently: Memorize ratio and root test conditions, along with Taylor and Maclaurin series expansions for standard functions.
- Track your error patterns: Keep a small log of mistakes from your Unit 10 AP Calc BC MCQs, note whether they’re algebraic, conceptual, or interpretation-based.
- Practice mixed question sets: Combine sequence and series topics to mimic real test variability.
If using UWorld, focus on its Unit 10 AP Calculus BC practice test questions that provide instant feedback and reasoning for each answer. Reviewing the explanations, especially for incorrect attempts, strengthens your understanding of how each convergence decision is made. Over time, this active learning method improves accuracy, pacing, and confidence for the AP Calculus BC Unit 10 exam.
How are infinite sequences and series connected in AP Calculus BC Unit 10?
In AP Calculus BC Unit 10, infinite sequences and series are two closely related ideas that form the backbone of advanced calculus. A sequence is an ordered list of numbers approaching a limit, while a series is the sum of those terms. Understanding how sequences lead to convergent or divergent series is essential for solving both AP Calc BC Unit 10 MCQs and FRQs.
Here’s how they connect:
- A convergent sequence approaches a single finite value, setting the groundwork for a convergent series.
- A series is formed by adding sequence terms; it converges only if the corresponding sequence of partial sums approaches a limit.
- Convergence tests; like the ratio, root, and alternating series tests, help determine whether infinite sums behave predictably.
- Taylor and Maclaurin series extend this logic by representing entire functions as infinite sums, letting you approximate complex behavior through polynomial terms.
Recognizing this relationship helps you understand why sequences and series are central to the AP Calculus BC Unit 10 review. They unify concepts from earlier units on limits and derivatives, allowing you to apply infinite reasoning to real-world and theoretical problems, a crucial skill for top performance on the AP Calc BC Unit 10 test.
How can I retain complex formulas and convergence tests in AP Calculus BC Unit 10?
Retaining the many convergence tests and formulas in AP Calculus BC Unit 10 can be challenging because the unit blends theoretical logic with procedural detail. Students often struggle to recall which test applies where, especially during AP Calc BC Unit 10 MCQs or timed FRQs. Building long-term recall requires structured repetition and visual organization.
Here’s how to strengthen retention:
- Create a categorized chart: Group tests by type: comparison, ratio, root, and alternating series and note each test’s condition for convergence or divergence.
- Use visual cues: Sketch convergence behavior or geometric representations for alternating and power series.
- Apply spaced repetition: Review your AP Calc BC Unit 10 formulas daily for short sessions rather than one long cram session.
- Practice through application: Work on Unit 10 AP Calculus BC practice questions that ask you to identify the correct convergence test.
- Summarize logic in your own words: After solving a question, restate why a test applies, this deepens conceptual memory.
For quick review, many students create a Unit 10 AP Calc BC cheat sheet summarizing test conditions, key formulas, and error bounds. Revisiting this sheet before practice sessions helps solidify recall and reduces second-guessing during the AP Calculus BC Unit 10 test.
How do I study infinite series and Taylor expansions for the Unit 10 test?
Mastering infinite series and Taylor expansions in AP Calculus BC Unit 10 means developing fluency with both theory and problem-solving. These topics often appear in Unit 10 AP Calc BC FRQs and MCQs, testing your ability to derive, approximate, and interpret function behavior using series.
Here’s a focused way to study effectively:
- Start with concept review: Revisit partial sums, convergence, and divergence. Understand how infinite processes build finite results.
- Memorize common series: Learn the Maclaurin series for sine, cosine, exponential, and logarithmic functions, as these recur frequently in AP Calc BC Unit 10 practice tests.
- Work through derivations: Don’t just memorize, practice deriving Taylor polynomials from the definition to grasp their logic.
- Connect to error estimation: Understand how remainder terms indicate the accuracy of approximations.
- Alternate practice formats: Combine untimed conceptual sets with timed quizzes to balance understanding and pacing.
These strategies ensure a deeper comprehension of how infinite processes model real functions, one of the most advanced applications in calculus. Regular mixed practice and review of feedback from progress check-style questions improve precision and confidence before the AP Calculus BC Unit 10 exam.
How can I improve my accuracy on AP Calculus BC Unit 10 MCQs and practice questions?
Improving accuracy on AP Calculus BC Unit 10 MCQs and practice problems requires consistent, targeted review of both conceptual understanding and computational precision. Unit 10 focuses heavily on infinite sequences, convergence, and series tests, which appear frequently across multiple-choice and free-response sections. The key is not just memorizing tests but knowing when and how to apply them.
Here’s how to build precision and consistency:
- Identify common traps: Review typical mistakes in ratio, root, and alternating series tests, especially sign errors or incorrect limit evaluation.
- Work progressively: Begin with untimed sets from your AP Calc BC Unit 10 study guide, then transition to timed quizzes that simulate exam pressure.
- Track your reasoning: Note which step causes errors; setup, test choice, or arithmetic and reattempt similar problems.
- Use visual cues: Sketch convergence behavior or partial sum graphs to reinforce understanding.
- Practice FRQs regularly: Many AP Calc BC Unit 10 FRQs include conceptual explanations about convergence that clarify theory beyond calculations.
Frequent review through structured progress check practice sets, such as those in UWorld, helps you refine logical reasoning, identify weak points, and approach Unit 10 AP Calculus BC review questions with confidence.
What is the best AP Calculus BC Unit 10 practice test format?
An ideal AP Calculus BC Unit 10 practice test mirrors the structure, pacing, and difficulty of the real exam while focusing on infinite sequences and series. A balanced format helps you evaluate both conceptual mastery and problem-solving endurance.
Here’s a recommended setup:
- 30–35 MCQs: Include a mix of convergence tests, partial sums, and Taylor or Maclaurin series. Alternate between calculator and non-calculator questions to reflect the AP format.
- 2 FRQs: One problem should test convergence/divergence using comparison or ratio tests; the other should focus on constructing or analyzing Taylor series representations.
- Timing: Complete the test in 60–70 minutes, followed by a short review session to analyze missed questions and identify patterns in reasoning errors.
- Reference Sheet: Keep your AP Calc BC Unit 10 formulas handy for quick recall during early practice rounds, but phase them out as you gain confidence.
Regular simulation of this format using Unit 10 AP Calculus BC practice tests strengthens endurance, accuracy, and timing, all critical for scoring well on the official exam. Reviewing test explanations afterward helps connect procedural work with conceptual understanding, a key differentiator between a 3 and a 5 on the AP Calculus BC test.
When should I begin preparing for the AP Calculus BC Unit 10 test?
The best time to start preparing for the AP Calculus BC Unit 10 test is while your class begins introducing infinite sequences and series. Since this unit ties together multiple previous topics; like limits, derivatives, and integration, steady review from the start helps you build a strong foundation. Early preparation prevents confusion between convergence tests and allows more time to practice Taylor and Maclaurin series, which often appear in both MCQs and FRQs.
Here’s a suggested preparation timeline:
- During Class Instruction: After each lesson, solve a few AP Calc BC Unit 10 practice problems on sequence behavior, convergence, and partial sums to reinforce understanding.
- 2 to 3 Weeks Before the Test: Review all major convergence tests; comparison, ratio, root, and alternating and attempt mixed sets from your AP Calculus BC Unit 10 study guide.
- One Week Before the Test: Take short, timed quizzes using AP Calc BC Unit 10 MCQs and FRQs focusing on Taylor polynomials, remainder terms, and error bounds.
- Final Days: Summarize key formulas and convergence criteria in a Unit 10 AP Calc BC cheat sheet for quick recall.
This structured timeline supports long-term retention, boosts problem-solving accuracy, and ensures confidence in every concept tested on the AP Calculus BC Unit 10 review and final exam.
What are the common mistakes students make in AP Calculus BC Unit 10?
Students often find AP Calculus BC Unit 10 one of the most challenging because it blends algebraic precision with conceptual reasoning. Missteps in identifying convergence or applying tests correctly can lower accuracy on both MCQs and FRQs. Understanding where errors typically occur helps you avoid them during your Unit 10 AP Calc BC review and practice sessions.
Common mistakes include:
- Confusing convergence tests: Applying the ratio test when the comparison or alternating series test is more appropriate.
- Ignoring test conditions: Forgetting to check that terms are positive or decreasing before using a specific test.
- Sign errors in alternating series: Neglecting the absolute value in ratio/root tests or mismanaging signs when series alternate.
- Overlooking interval of convergence: Failing to test endpoints when finding power series intervals.
- Misinterpreting remainders: Confusing the meaning of the remainder term in Taylor and Maclaurin series approximations.
To minimize these mistakes, practice structured AP Calc BC Unit 10 progress check MCQs and FRQs that include rationales for both correct and incorrect reasoning. Reviewing solutions instead of just final answers improves conceptual clarity and ensures stronger performance on the AP Calculus BC Unit 10 test.
Where can I find AP Calculus BC Unit 10 notes, cheat sheets, or study guides?
Reliable AP Calculus BC Unit 10 notes and study guides summarize key ideas from infinite sequences and series, making it easier to review convergence tests and Taylor expansions efficiently. Look for resources that align with the College Board’s Course and Exam Description (CED) to ensure full topic coverage.
Here’s what a useful study guide should include:
- Formulas and Definitions: Essential AP Calc BC Unit 10 equations, such as nth-term tests, ratio and root test formulas, and Taylor/Maclaurin series expansions.
- Examples: Worked problems showing step-by-step reasoning for convergence and divergence.
- Visual Aids: Graphs illustrating partial sums and convergence behavior.
- Cheat Sheets: Quick-reference summaries that condense test conditions and formulas into a single page for efficient review.
UWorld’s AP Calc BC Unit 10 study guide complements classroom instruction with visual explanations, progress-check practice questions, and targeted review tools. Pairing it with official College Board outlines ensures complete readiness for the AP Calculus BC Unit 10 review and exam.
Are there downloadable AP Calculus BC Unit 10 study guide PDFs and practice materials?
Yes. You can find downloadable AP Calculus BC Unit 10 study guide PDFs and practice materials that simplify complex topics like infinite sequences, series convergence, and Taylor expansions. These resources are great for structured review and quick revision before tests.
When selecting materials, look for:
- Topic coverage: Ensure the guide includes convergence and divergence tests, ratio and root test examples, and Taylor/Maclaurin series derivations.
- Exam-style practice: Choose worksheets or AP Calc BC Unit 10 practice tests with both MCQs and FRQs modeled after real exam questions.
- Answer rationales: Resources with detailed explanations help you understand your reasoning process and correct mistakes efficiently.
UWorld provides downloadable and printable AP Calc BC Unit 10 review PDFs, flashcards, and practice sets that combine theory with application. Using these alongside official College Board content gives you a comprehensive, self-paced approach to mastering Unit 10 AP Calculus BC before exam day.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Differential Equations
Applications of Integration
Parametric Equations, Polar Coordinates, and Vector-Valued Functions