Bundle 3+ College Prep products for 20% off

AP® Calculus AB Unit 5 Review and Practice Test

Analytical Applications of Differentiation

Prepare for your AP® Calculus AB Unit 5 test with our complete Analytical Applications of Differentiation review. This unit deepens your understanding of how derivatives describe function behavior, including extrema, concavity, and motion. You’ll learn to apply derivatives to real-world contexts, analyze graphs, and solve optimization problems with precision. Our AP Calc AB Unit 5 review combines high-yield video lessons, an interactive study guide, and Unit 5 practice tests that reflect the actual AP exam format.

AP Calculus AB prep course suite by UWorld

Boost Your Confidence and Score High with Our AP Calculus AB Unit 5 Review

Master AP Calculus AB Unit 5: Analytical Applications of Differentiation with all the tools you need to succeed. This AP Calc AB Unit 5 review explains how derivatives describe function behavior, from identifying extrema and points of inflection to analyzing concavity and motion. Strengthen your problem-solving skills with unit 5 AP Calc AB practice tests and MCQs that mirror the style and difficulty of the actual exam, and reinforce every concept through UWorld’s detailed Unit 5 study guide and step-by-step lessons.

Watch

Engaging Video Lessons

Understand how derivatives reveal the behavior of functions with short, visual lessons designed for clarity. UWorld’s AP Calculus AB Unit 5 videos simplify complex ideas like concavity, extrema, and optimization, showing how each connects to real-world motion and rates of change. These AP Calc AB Unit 5 video lessons use step-by-step visualizations to make problem-solving intuitive, helping you review efficiently before your next quiz or exam.

Preview Video Lesson
Buy Now
UWorld’s AP Calc AB Video Lessons and Online Study Guide
UWorld’s AP Calculus AB Study Guide Prep book
Read

Interactive Study Guides

Our AP Calculus AB Unit 5 study guide covers every topic in the College Board’s CED. Built-in knowledge checks reinforce your understanding of extrema, concavity, and optimization, so you know exactly what to review for your AP Calc AB Unit 5 review.

Preview Book
Buy Now
Practice

Try These AP Calculus AB Unit 5 Practice Test Questions

Get exam-ready with AP Calculus AB Unit 5: Analytical Applications of Differentiation practice tests. Our AP Calc AB Unit 5 practice tests include exam-style problems that strengthen your understanding of extrema, concavity, and optimization. Use this unit 5 AP Calculus AB review to sharpen your derivative applications and build the confidence to excel on test day.
Try these sample practice questions with detailed answer explanations:
Analytical Applications of Differentiation Practice Tests

Question

The derivative of a continuous function f is given by f ′ (x) = 4 x 2 - 12 x 2 for x > 0. If f(1) = 16 and f(4) = 19, what value of x in the open interval (1, 4) satisfies the conclusion of the Mean Value Theorem for f on the closed interval [1, 4] ?

A. 1
B. 3
C. 2 3
D. 2

Hint :

The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value in the interval (a, b).

Explanation

The Mean Value Theorem (MVT) guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change (AROC) of f on [a, b] for at least one x-value c in the interval (a, b).

Instantaneous rate

To determine the value of x = c that satisfies the MVT for f on the closed interval [1, 4], first use the given function values to calculate the (AROC) of f(x) on [1, 4].

f (4) - f (1) 4 - 1 AROC formula for a = 1 and b = 4
19 - 16 4 - 1 Plug in f(4) = 19 and f(1) = 16
1 Simplify

The average rate of change of f(x) on [1, 4] is equal to 1, so set the given instantaneous rate of change  f ′ (x) = 4 x 2 - 12 x 2 equal to the average rate of change 1 and solve for x.

4 x 2 - 12 x 2 = 1 Set instantaneous rate of change equal to AROC
4 x 2 - 12 = x 2 Multiply both sides by x2
3 x 2 = 12 Add 12 and subtract x2 on both sides
x 2 = 4 Divide both sides by 3
x = ± 2 Take the square root of both sides

The solution x = −2 is not in the interval (1, 4), so the only value that satisfies the MVT for f on the closed interval [1, 4] is x = 2.

(Choice A) 1 is the value of the average rate of change of f on [1, 4], but the question asks for the value of x that satisfies the MVT on [1, 4].

(Choice B) 3  may result from mistakenly setting f ′ equal to zero instead of setting f ′ equal to the average rate of change.

(Choice C) 2 3  may result from incorrectly calculating the average rate of change as 3.

Things to remember:
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value in the interval (a, b).

Question

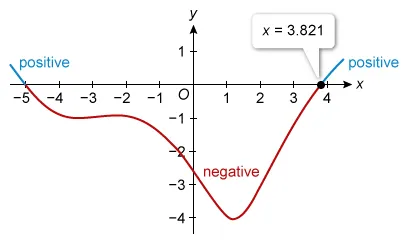
The function g is defined by g (x) = - 5 + 6 + x 2 - 7   sin   x . If the function f is an antiderivative of g, which of the following is the x-coordinate of the location of a local minimum for the graph of y = f(x) ?

A. −5.058
B. −3.391
C. 1.216
D. 3.821

Hint :

An antiderivative f of a function g is any function whose derivative is g.

Explanation

An antiderivative f of a function g is any function whose derivative is g. It is given that f is an antiderivative of g, so the derivative of f is g.

Antiderivative of g

A local (relative) minimum on the graph of f(x) occurs at any value of x where f′(x) = g(x) is zero or undefined (a critical point on the graph of f) and changes from negative to positive.

To find the x-value of the relative minimum of f, graph its derivative  g (x) = - 5 + 6 + x 2 - 7   sin   x  and locate any zeros where the graph changes from negative to positive.

The graph Positive Negative

The graph of f ′ = g changes from negative to positive at only one point, so the graph of y = f(x) has a relative minimum at x = 3.821.

(Choice A) −5.058 is the x-coordinate of a local maximum on the graph of f, but the question asks for the x-value of a local minimum.

(Choices B and C) −3.391 and 1.216 are x-coordinates of relative minimums on the graph of g(x), but the question asks for a relative minimum on the graph of f(x) = g ′(x).

Things to remember:

  • An antiderivative of a function f is any function F whose derivative is f.

  • A local minimum of a continuous function f(x) occurs at any value of x at which f ′(x) is zero or undefined and f ′ changes from negative to positive.

Question

The function f is continuous on the closed interval [−1, 5]. If f(−1) = −3 and f(5) = 3, which of the following conditions would guarantee that there is a number c in the open interval (−1, 5) where f ′(c) = 1 ?

A.

f is differentiable on the open interval (−1, 5).
B. f is not differentiable on the open interval (−1, 5).
C. lim x → k f (x) = f (k) for all k on the open interval (−1, 5).
D. f ′(k) = 0 for at least one value of k in the open interval (−1, 5).

Hint :

The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).

Explanation

The Mean Value Theorem (MVT) guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).

To guarantee there is a number c in the open interval (−1, 5) where f ′(c) = 1, first verify the average rate of change is 1 between the given points f(−1) = −3 and f(5) = 3 (calculation).

The MVT guarantees that f ′(c) = 1 if the MVT conditions are met for f on the interval [−1, 5]. It is given that f is continuous on [−1, 5], but no information is given about the differentiability of f on (1, 5).

The MVT applies to the continuous function f on [−1, 5] and guarantees that f ′(c) = 1 for at least one value of c in (−1, 5) only if f is differentiable on the open interval (−1, 5).

(Choice B) "f is not differentiable on the open interval (−1, 5)" indicates that the MVT does not apply to the function on the interval, but the question implies that the MVT does apply.

(Choice C) " lim x → k f (x) = f (k) for all k on the open interval (−1, 5)" indicates that the function is continuous on the open interval, but the MVT also requires differentiability.

(Choice D) "f ′(k) = 0 for at least one value of k in the open interval (−1, 5)" is the conclusion of Rolle's Theorem, but the question requires justifying the conditions of the MVT.

Things to remember:
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).

Buy Now
UWorld Dark Blue logo

Study Anywhere, Anytime

Tackle AP Calculus AB Unit 5 practice tests on the go, review topic videos between classes, or dive into your study guide while waiting for friends. Everything you need for your AP Calculus AB Unit 5 review is always at your fingertips with the UWorld app.

App Store
Google Play

Stand Out
with a Top Score in AP Calculus AB

Complete your AP Calculus AB Unit 5 review and keep building your mastery across all units with UWorld. Achieving a top score can enhance your academic profile and open doors to competitive college programs and scholarship opportunities.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc AB Videos
  • Print & Digital Study Guide
  • 1400+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards & Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calculus AB Unit 5, titled Analytical Applications of Differentiation, focuses on using derivatives to analyze how functions behave. This unit explains how to determine where a function is increasing or decreasing, identify extrema, analyze concavity, and locate inflection points. Students also explore optimization and motion problems, applying derivatives to real-world and graphical contexts. Mastering these ideas is key to understanding relationships between variables and preparing for integration topics in later units.

UWorld’s AP Calculus AB Unit 5 review and study guide provide visual examples, detailed explanations, and real exam-style problems. This structured approach helps you connect theory with application and gain the confidence to succeed on your AP Calc AB Unit 5 test or practice test.

Unit 5 AP Calc AB, also known as Analytical Applications of Differentiation, builds on derivative concepts to help students interpret and predict function behavior. This unit focuses on applying derivatives to real-world and theoretical problems through graphical, numerical, and analytical reasoning.

Key topics covered include:

  • Extrema and Critical Points: Using derivatives to locate local and absolute maxima and minima.
  • Concavity and Inflection Points: Determining where a function curves upward or downward and identifying changes in curvature.
  • The First and Second Derivative Tests: Analyzing function behavior to justify increasing/decreasing intervals and concavity.
  • Optimization Problems: Solving real-world scenarios involving maximum or minimum values.
  • Motion and Rate-of-Change Applications: Applying derivatives to describe velocity, acceleration, and movement along a curve.

UWorld’s AP Calculus AB Unit 5 study guide and QBank are aligned with the College Board’s Course and Exam Description (CED). Each topic includes AP Calc AB Unit 5 practice test questions and visual explanations to make your AP Calculus AB Unit 5 review efficient, targeted, and exam-ready.

A well-designed AP Calculus AB Unit 5 study guide should teach both the “why” and the “how” behind each derivative application. UWorld’s print and digital materials for AP Calc AB Unit 5 follow the College Board’s CED and walk you through analytical applications of differentiation; covering extrema, concavity, inflection points, and optimization. Every section includes short self-check activities and quick practice examples that confirm your grasp of each concept before you move ahead.

The AP Calculus AB Unit 5 notes PDF, available in the UWorld app, features visual graphs, concise explanations, and built-in flashcards with a personalized planner for flexible study sessions. You can also try a free trial to explore how UWorld’s integrated read-watch-practice method streamlines your learning compared with typical class notes or online worksheets. While additional College Board or classroom resources can complement your preparation, UWorld’s platform should be your main source for a complete, efficient AP Calculus AB Unit 5 review.

The AP Calculus AB Unit 5 test focuses on applying derivatives to analyze and interpret the behavior of functions. Students encounter both multiple-choice and free-response questions that assess their understanding of extrema, concavity, and optimization concepts introduced in this unit.

Common question types include:

  • Graphical analysis of increasing/decreasing intervals and points of inflection.
  • Derivative-based justifications using the First and Second Derivative Tests.
  • Optimization problems involving real-world maximum and minimum values.
  • Motion and related rates questions connecting velocity, acceleration, and position.
  • Interpretation of graphical data and reasoning from slope and tangent behavior.

UWorld’s AP Calc AB Unit 5 review and practice tests mirror these formats, featuring problems that reflect the rigor and style of the actual exam. Each AP Calculus AB Unit 5 practice test includes detailed visual explanations, helping you master every topic in Analytical Applications of Differentiation.

Before taking your AP Calculus AB Unit 5 test, make sure you have a strong understanding of the fundamental derivative concepts introduced in earlier units. You should be able to calculate derivatives accurately, interpret their meaning, and apply them to real-world and graphical scenarios.

Key concepts to review include:

  • Identifying and classifying critical points, extrema, and inflection points.
  • Applying First and Second Derivative Tests to determine function behavior.
  • Solving optimization problems involving maximum and minimum values.
  • Understanding how concavity and slope describe motion, acceleration, and rates of change.
  • Analyzing graphical representations to predict behavior using the derivative relationship

UWorld’s AP Calculus AB Unit 5 study guide, video lessons, and practice tests give you all the tools you need to strengthen these skills. By reading concise explanations, watching step-by-step demonstrations, and practicing with AP Calc AB Unit 5 review questions, you’ll gain the confidence and accuracy needed to excel on both unit tests and the full AP Exam.

Yes. UWorld offers a free trial that gives you access to selected AP Calculus AB Unit 5 practice tests, multiple-choice questions, and visual explanations from expert instructors. This allows you to experience how derivative applications are taught and tested before subscribing to the full program.

The free version highlights how UWorld’s AP Calc AB Unit 5 review platform connects theory with practice, helping you learn how extrema, concavity, and optimization appear in real exam questions. You can explore how each problem is broken down step by step, with graphs and reasoning that reinforce understanding.

Combining the UWorld free trial with official College Board materials or classroom notes creates a balanced study plan. However, UWorld remains the most efficient primary resource for mastering the analytical applications of differentiation and preparing for your AP Calculus AB Unit 5 test.

While a full study plan is always best, UWorld provides concise reference tools that can serve as an effective AP Calculus AB Unit 5 cheat sheet for quick review. These summaries highlight essential derivative concepts and applications from Analytical Applications of Differentiation, making them perfect for last-minute study sessions or on-the-go practice.

Key topics covered in these short reference materials include:

  • Rules for finding extrema, concavity, and inflection points.
  • Optimization strategies using derivatives.
  • First and Second Derivative Tests for analyzing graphs.
  • Real-world motion and rate-of-change applications.
  • Critical terms and formulas essential for the AP Calc AB Unit 5 test.

These quick references are available through the UWorld app, along with flashcards and AP Calculus AB Unit 5 notes PDF materials for structured learning. They’re designed to complement, not replace, full-length AP Calculus AB Unit 5 review and practice tests that provide deeper understanding and exam readiness.

The most effective AP Calculus AB Unit 5 flashcards focus on key derivative applications and help reinforce understanding through active recall and repetition. UWorld’s flashcard system is designed to complement your AP Calc AB Unit 5 review, offering structured practice on critical Unit 5 concepts and definitions from Analytical Applications of Differentiation.

Each deck includes:

  • Core terminology such as extrema, concavity, inflection point, and optimization
  • Step-by-step derivative strategies and problem-solving reminders
  • Concept links connecting derivatives to motion, velocity, and acceleration
  • Graph-based examples that visualize how derivatives describe function behavior

UWorld’s digital flashcard system works seamlessly across devices and adapts to your performance using spaced repetition to improve long-term retention. You can tag tricky topics for extra review, track progress, and instantly connect each flashcard to related AP Calculus AB Unit 5 practice questions for complete reinforcement.

A strong AP Calculus AB Unit 5 review integrates reading, watching, and active practice. UWorld combines all these methods in one structured platform to help you master Analytical Applications of Differentiation.

  • Read: Begin with UWorld’s AP Calculus AB Unit 5 study guide, featuring clear explanations and visual graphs that simplify concepts like extrema, concavity, inflection points, and optimization.
  • Watch: Learn through UWorld’s high-yield video lessons that break down derivative applications into real-world examples, showing how slope, motion, and rate of change connect to function behavior.
  • Practice: Strengthen comprehension with AP Calc AB Unit 5 practice tests and problem sets designed to mirror the real exam. Each question includes step-by-step solutions and visual reasoning to reinforce accuracy.
  • Active Recall & Spaced Repetition: Use UWorld’s adaptive flashcard system to revisit challenging calculus concepts and formulas at spaced intervals, improving retention and long-term understanding.
  • Timed Practice: Simulate real exam conditions with the AP Calculus AB Unit 5 test to build pacing, focus, and problem-solving efficiency under pressure.
  • Targeted Review & Tracking: Use UWorld’s progress dashboard to analyze results, identify weak areas, and track growth through analytics that show improvement over time during your AP Calculus AB Unit 5 review.

UWorld’s integrated approach ensures comprehensive preparation, guiding you from concept mastery to confident performance on your AP Calculus AB Unit 5 test and the full AP Exam.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus AB by exploring related units that build on these concepts.
Unit 1

Limits and Continuity
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 4

Contextual Applications of Differentiation
Unit 6

Integration and Accumulation of Change
Unit 7

Differential Equations
Unit 8

Applications of Integration
Scroll to Top

Crack AP Calc AB

Get Exam Ready
In Less Time
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.