Bundle 3+ College Prep products for 20% off

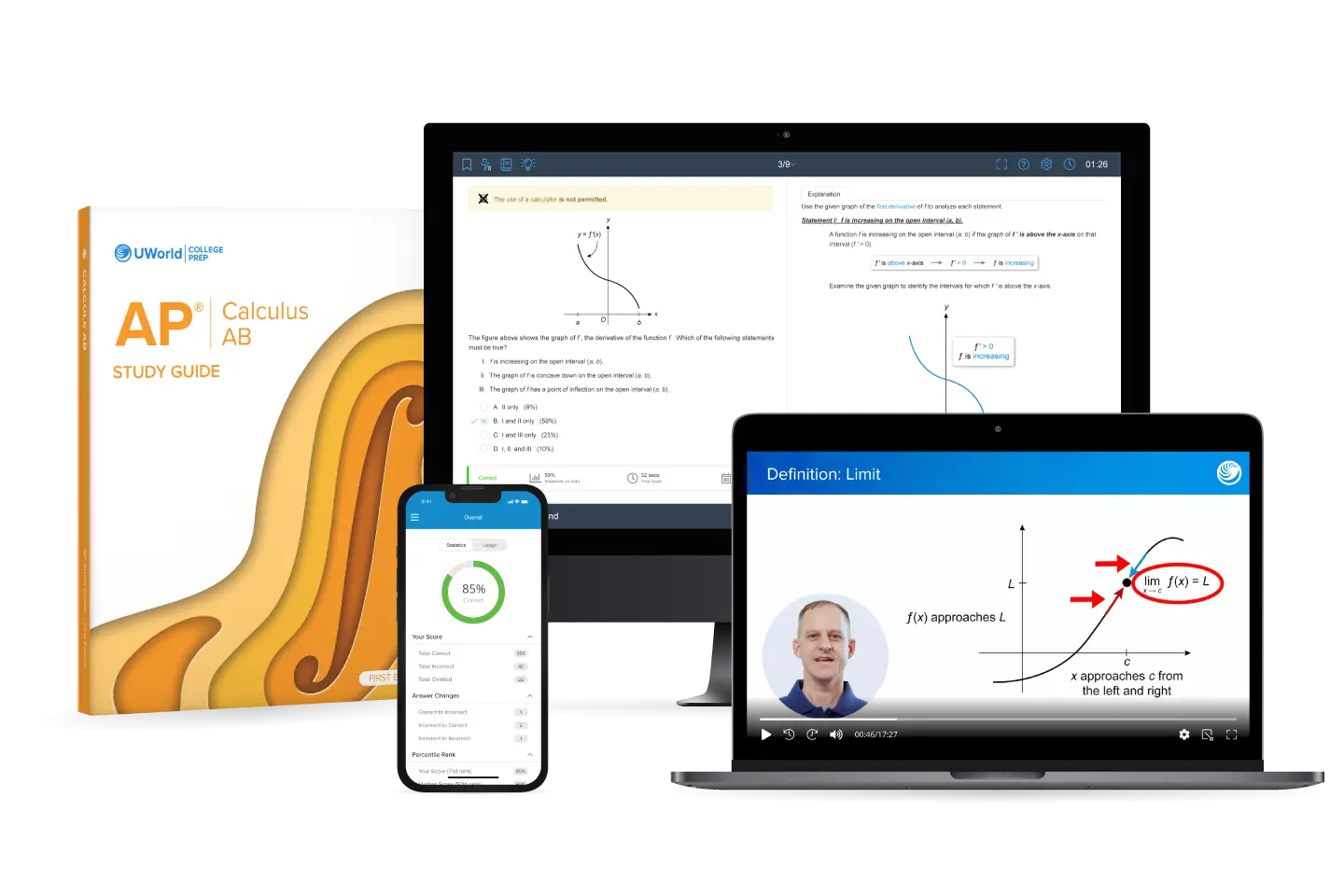
AP Calculus AB Unit 4 Review and Practice Test

Contextual Applications of Differentiation

Grasp the real-world power of derivatives, bridging pure calculus and applied motion, showing how rates of change drive everything from velocity to optimisation. UWorld’s AP® Calculus Unit 4 review covers everything you need to tackle the toughest MCQs and FRQs confidently. Through interactive videos, expertly-written study guides, and exam-style practice questions, you’ve got all the tools to succeed in the exam in one integrated platform.

AP Calculus AB prep course suite by UWorld

Solve Real-World Calculus Problems Accurately
with Our AP Calc AB Unit 4 Review

From learning about motion, optimization, and related rates, you master the application of derivatives with resources that simplify complex differential problems into clear, visual explanations that help you connect calculus to real-world problems.

Watch

See Differentiation in Action

Are you wondering about motion, growth, and chance? Don’t worry; our engaging video library turns abstract derivatives into stories you remember. Learn how velocity and acceleration connect, interpret slope and concavity, and how related rates tie multiple variables together. Each video is expertly stitched to be concise, visually clear, and loaded with AP-exam level examples.

Preview Video Lesson
Buy Now
UWorld’s AP Calc AB Video Lessons and Online Study Guide
UWorld’s AP Calculus AB Study Guide Prep book
Read

Understand Derivatives Beyond Formulas

Don’t let your brain think that you need to memorize concepts. With UWorld’s interactive study guides for Unit 4, each section combines visuals, examples, and summaries to help you interpret derivatives in context. Go from understanding to reasoning and solving scenarios. You’ll see how calculus explains real-life change with a step-by-step guide.

Preview Book
Buy Now
Practice

Strengthen Your Understanding of AB Unit 4 via Real-Exam Questions

UWorld’s AP Calculus AB Unit 4 practice questions are powered with detailed explanations and mirror the real-exam environment, so you develop exam endurance. With timed-practice tests and analytics, you can work on your shortcomings and avoid common derivative mistakes. Learn how to step up equations, use correct notation, and think like an AP grader.
Try these sample practice questions with detailed answer explanations:
Contextual Applications of Differentiation Practice Tests

Question

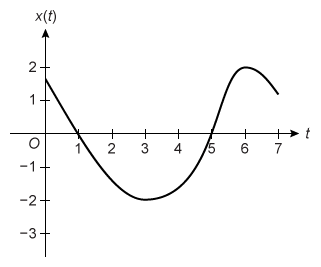
The graph above shows the position x t at time t of a particle moving along a straight line for 0 < t < 7 The graph has horizontal tangents at t = 3 and t = 6 and a point of inflection at t = 5 . For what values of t is the velocity of the particle decreasing?

A. 0 < t < 5
B. 5 < t < 7 only
C. 0 < t < 3 and 6 < t < 7
D. 0 < t < 1 and 5 < t < 7

Hint :

The velocity v t of a particle moving along a straight line is decreasing when v ′ t < 0

Explanation

To determine the interval(s) on which the velocity of a particle is decreasing from the graph of the position function, first recall that the velocity function v(t) is the derivative of the position function x(t).

v ( t ) = x ′ ( t )

If the velocity is decreasing, then the derivative of velocity v'(t) must be negative and therefore the second derivative of the position function x''(t) must also be negative.

v ′ ( t ) < 0
⇓
x ″ ( t ) < 0

The second derivative of a function determines the concavity of its graph. Since x''(t) < 0, identify where the graph of x(t) is concave down.

The graph of x(t) has a point of inflection at t = 5, so the graph changes concavity at that point.

The graph of x(t) is concave down on the interval 5 < t < 7, so the velocity is decreasing on 5 < t < 7 only.

(Choice A) 0 < t < 5 is the interval on which the velocity is increasing, but the question asks for the interval on which the velocity is decreasing.

(Choice C) 0 < t < 3 and 6 < t < 7 may be a result of identifying the intervals on which the velocity is negative rather than the interval on which the velocity is decreasing.

(Choice D) 0 < t < 1 and 5 < t < 7 may be a result of identifying intervals on which x(t) > 0 rather than on which the velocity is decreasing.

Things to remember:

To determine when the velocity of a function is decreasing from the graph of its position function, identify when the graph of x(t) is concave down.

Question

The volume of a cube with edges of length x centimeters is given by V = x 3 cubic centimeters. If the volume of the cube is increasing at a constant rate of 45 cubic centimeters per minute, at what rate is x changing, in centimeters per minute, with respect to time at the instant when x = 3 ?

A. 5 3
B. 5 2
C. 15
D. 5

Hint :

To solve a related rates problem, first identify the rate to be found, the given rate, and any other given values.

Explanation

The rate at which a quantity changes is given by the derivative of that quantity with respect to time. To solve a related rates problem in which one rate is given and another rate is to be found, first identify the rate to be found, when it is to be found, and the given rate.

To find the rate at which x is changing with respect to time dx dt when x = 3 , differentiate both sides of the volume equation with respect to time t. Then plug in the given values for dV dt and x and solve for dx dt .

V=x3 Volume of a cube with edge length x
dV dt = 3x2 dx dt Differentiate both sides with respect to t: d dt [un] =nun-1 dudt
45=3(3)2 dxdt Plug in dVdt=45 and x=3
45=27 dxdt Simplify right side: 3(3)2=3(9)=27
45 27 = dxdt Divide both sides by 27
5 3 = dxdt Reduce: 45 27 = 5·9 3·9 = 53

Therefore, x is changing at the rate of 5 3 centimeters per minute at the instant when x = 3 .

(Choice B) 52 may be a result of incorrectly differentiating the given expression for volume: ddt [x3] ≠ 3·2 dxdt .

(Choice C) 15 may be a result of improperly differentiating the volume equation to get dVdt =3x2 and solving for x rather than differentiating both sides of the volume equation with respect to t to get dVdt =3x2 dxdt and solving for dxdt .

(Choice D) 5 may be a result of neglecting to multiply by 3 when differentiating the expression for volume: ddt [x3] ≠ x2 dxdt .

Things to remember:

  • To solve a related rates problem in which one rate is given and another rate is to be found, first identify the rate to be found, when it is to be found, and the given rate.

Question

lim x → 1 2 [ sin ( 2 πx ) ln ( 2 x ) ] is

A. - π
B. 0
C. π
D. nonexistent

Hint :

To evaluate a limit of the form lim x → c f ( x ) g ( x ) , first directly substitute x = c into the function.

Explanation

To evaluate a limit of the form lim x → c f ( x ) g ( x ) , first directly substitute x = c into the function and simplify. If the result yields an indeterminate form, apply L'Hospital's Rule.

lim x → 1 2 [ sin ( 2 π x ) ln ( 2 x ) ] Given limit
sin ( 2 π · 1 2 ) ln ( 2 · 1 2 ) Plug in x = 1 2
0 0 Evaluate: sin π = 0 and ln 1 = 0

Direct substitution results in the indeterminate form 0 0 , so apply L'Hospital's Rule by differentiating the numerator and denominator independently, and then evaluate the limit again.

The numerator and denominator are composite functions of the form sin u and ln u , so use the chain rule to differentiate.

lim x → 1 2 d d x [ sin ( 2 πx ) ] d d x [ ln ( 2 x ) ] Apply L'Hospital's Rule
lim x → 1 2 2π cos ( 2πx ) 1 x Differentiate numerator and differentiate denominator independently
- 2 π 2 Evaluate limits of numerator and denominator
- π Simplify

Therefore, lim x → 1 2 [ sin ( 2 πx ) ln ( 2 x ) ] is −π.

(Choice B) 0 may result from assuming the indeterminate form 0 0 = 0.

(Choice C) π may result from using an incorrect derivative: d dx [ sin x ] ≠ − cos x.

(Choice D) "Nonexistent" may result from assuming that the indeterminate form 0 0 means that the limit does not exist.

Things to remember:

  • If a limit yields an indeterminate form, apply L'Hospital's Rule: Differentiate the numerator and denominator independently and then evaluate the limit.
Buy Now
UWorld Dark Blue logo

Study That Travels With You

From solving derivative problems during study hall to watching short videos between classes and reviewing concepts on the bus, UWorld’s app is the perfect travel companion. Turn every spare moment into score-boosting AP Calculus AB Unit 4 practice sessions.

App Store
Google Play

Stand Out
with a Top Score in AP Calculus AB

Finish your AP Calculus AB Unit 4 review and continue mastering all units with UWorld. Boost your performance and make yourself a standout candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc AB Videos
  • Print & Digital Study Guide
  • 1400+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards & Digital Notebook
  • Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calc AB Unit 4 focuses on applying derivative concepts to real-world contexts. You’ll explore motion problems, optimization, related rates, and differentiation in modeling change. Connect calculus notation to interpretation, and understand how the derivative describes velocity, acceleration, and growth trends. Key areas include:

  • Applying understanding of differentiation to problems involving motion
  • Identifying relevant mathematical information in verbal representations of real-world problems involving rates of change
  • Generalizing understandings of motion problems to other situations involving rates of change
  • Solving related rates problems
  • Local linearity and approximation
  • L’Hospital’s rule

The unit builds your ability to think contextually by translating words into equations, equations into graphs, and graphs into conclusions. It’s one of the most application-heavy sections of AP Calculus AB and is essential for success on the progress check FRQs and the whole exam.

Preparation should focus equally on concept understanding and problem application. Review the derivative rules from earlier units, then connect them to real-world motion and rate problems. Here’s what UWorld’s experts recommend:

  • Review foundational differentiation formulas and meanings
  • Watch video lessons on particle motion and related rates
  • Work through the Unit 4 study guide examples, paying attention to how equations are modeled from words
  • Practice FRQs and MCQs from the Unit 4 Qbank
  • Revisit errors, ensuring you understand the logic behind each step

Timed practice is key. AP questions often test your ability to interpret results quickly, like determining whether a particle is speeding up or slowing down. The more you practice under pressure, the more fluent your calculus reasoning becomes.

Yes. UWorld provides a 7-day free trial including Unit 4 lessons, study materials, and practice questions. It’s ideal for testing how our platform explains contextual applications of differentiation with clarity and depth. UWorld’s AP Calculus AB Unit 4 review includes video walkthroughs, interactive study guides, timed practice tests, and detailed explanations for each question. They go beyond explaining what, how, and why, preparing you with professional guidance.

Once you upgrade, you can access the review course to cover every unit anytime. Also, you can use College Board and Khan Academy’s resources to supplement your UWorld review, and see the difference for yourself. What makes UWorld stand out is its focus on active learning methodology that follows the watch, read, and practice way of studying. Look no further than the resources offered by the best AP instructors.

The AP Calculus AB Unit 4 test involves applying derivatives to real-world and contextual problems. Expect a blend of multiple-choice questions (MCQs) that assess conceptual understanding and free-response questions (FRQs) that measure your ability to reason, explain, and connect calculus to real motion or geometric change.

In the MCQ section, you’ll encounter questions involving position, velocity, and acceleration relationships in particle motion. Based on the signs of derivatives, you can also expect problems with optimisation, related rates, and whether a particle is speeding up or slowing down.

FRQs are typically multi-step and require interpretation. You might write equations for motion, justify sign changes, or explain results in context (“The particle is moving left because velocity < 0”). UWorld’s AP Calculus AB Unit 4 practice tests replicate this exam style perfectly, helping you transition from pure computation to complete analytical reasoning.

Improving your FRQ performance for Unit 4 depends on mastering how to explain calculus in words. AP graders don’t just want correct math; they want evidence of understanding. Each response must show logical progression from setup to conclusion, with supporting explanations at every step.

Here’s how you can refine your FRQ strategy:

  • Restate the problem setup clearly by defining variables and what each represents.
  • Show complete differentiation steps with logical progression.
  • Include units and context, and ensure that everything is clearly explained.
  • Label extrema correctly in optimization problems, explaining why they are maxima or minima.
  • Justify your reasoning, so graders don’t have to infer your logic.

Practicing under exam conditions with UWorld’s related rates and particle-motion FRQs is critical. Reviewing their detailed explanations helps you internalize phrasing, structure, and notation that align with AP grading rubrics, and ensure partial credit even when the final value isn’t perfect.

Unit 4: Contextual Applications of Differentiation typically represents 10-15% of the AP Calculus AB exam. Its influence extends far beyond that percentage because the concepts of motion, optimization, and related rates appear repeatedly throughout the course and in future AP Calculus BC content.

This unit serves as a crucial bridge between computation and application. You’ll use it in graph interpretation, modeling change, and solving real-world rate problems. Both multiple-choice and free-response sections include derivative-based questions that rely on Unit 4 logic, especially in interpreting acceleration, concavity, and slope changes.

The unit is a transition point where calculus becomes analytical thinking, and investing extra time here yields long-term score payoff on every subsequent unit and the cumulative exam.

The best AP Calculus AB Unit 4 study guide doesn’t just list formulas, but helps you connect why derivatives work in applied settings. UWorld’s interactive study guide delivers that balance of clarity, visualization, and exam relevance.

A comprehensive Unit 4 guide should include:

  • Concise explanations
  • Color-coded visuals
  • Worked examples that model AP-style FRQs, including setup and justification
  • Practice checkpoints after every section to reinforce understanding
  • Common error alerts explaining why students lose points on progress checks.

UWorld’s guide builds conceptual depth through structured visuals and layered examples. Pair it with the video lessons and Unit 4 progress check practice questions for an integrated review experience. This way, you’ll remember the steps and internalize how derivatives describe change in any context.

Yes. UWorld provides dedicated AP Calculus AB Unit 4 practice tests mirroring the format, rigor, and style of the College Board exam. Each test focuses on the contextual applications of differentiation, helping you apply theoretical understanding to particle motion, optimization, and related-rates problems with full-length explanations.

These practice sets include both MCQs and FRQs. The MCQs sharpen your recognition of calculus patterns while FRQs strengthen your ability to reason, write, and justify solutions step by step. Every question comes with a line-by-line explanation, covering equation setup, differentiation, and interpretation of results.

By consistently working through these Unit 4-specific tests, you’ll recognize AP-style phrasing, develop stronger analytical instincts, and improve accuracy and speed. These targeted drills are ideal for Unit 4 progress checks, midterms, or your final AP Calculus AB exam prep.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus AB by exploring related units that build on these concepts.
Unit 1

Limits and Continuity
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 5

Analytical Applications of Differentiation
Unit 6

Integration and Accumulation of Change
Unit 7

Differential Equations
Unit 8

Applications of Integration
Scroll to Top

Crack AP Calc AB

Get Exam Ready
In Less Time
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.