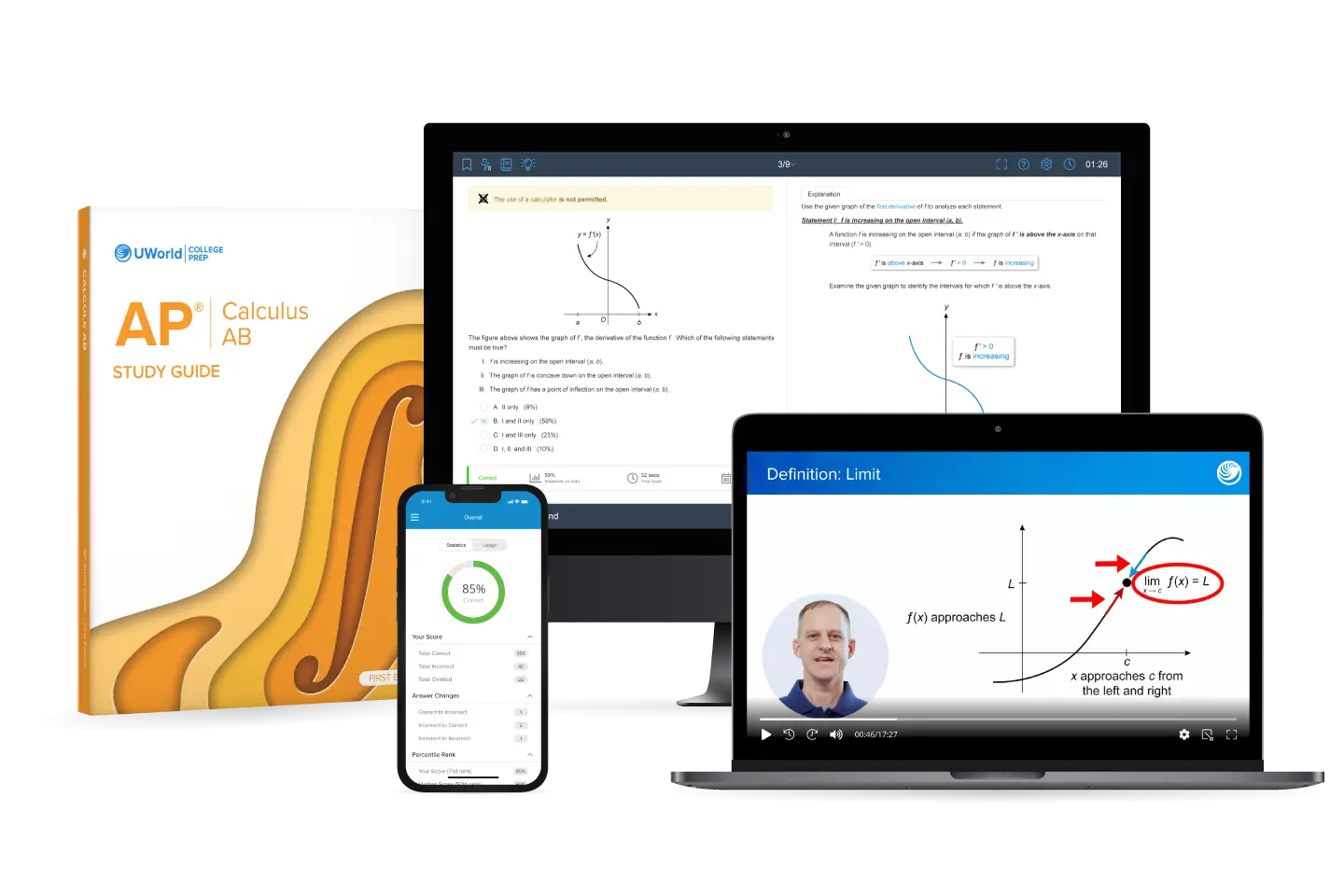
AP® Calculus AB Unit 3 Review and Practice Test

Differentiation: Composite, Implicit, and Inverse Functions

Mastering differentiation in AP® Calc AB can just be your turning point in the exam. With UWorld’s AP Calc AB Unit 3 review, you’ll move beyond basic rules and learn how derivatives reveal deep relationships between functions. Each concept is taught through interactive video, guided explanations, and AP-style practice tests that mirror the official exam. Go from tackling tough questions to understanding and strategically solving each confidently.

Approach Every Problem Confidently with Our AP Calculus AB Unit 3 Review

Stay ahead of your mates by developing a firm grasp of differentiation techniques, with the only review you need to score higher in the exam. UWorld’s AP Calc AB Unit 3 review breaks down complex functions into simple, solvable parts with videos, examples, and practice problems that mirror the AP exam style.

Watch

From Chain Rule to Inverse Derivatives, Visualize Each of Them

Our extensive video library covers each concept, be it the chain rule, implicit differentiation, or the derivative of inverse functions, with real AP examples and step-by-step problem solving, so you don’t have to worry about memorizing. These videos help you recognize patterns, apply formulas quickly, focus on logic, and avoid common derivative mistakes.

Preview Video Lesson

Read

Simplify Every Differentiation Problem

Powered by interactive visuals that take you through the logic behind, UWorld’s interactive study guides take a step further by focusing on example-based learning and summaries that make calculus rules stick. Understand when and why to use the chain rule, master implicit equations, and how inverse functions' derivatives relate to slope reciprocity.

Practice

Sample Questions That Make the Difference

Tackle AP-style unit 3 differentiation problems that teach you how to set up, solve, and explain derivative relationships. Take timed practice tests and analyze detailed solutions describing how and why each step works, which is ideal for mastering MCQs and FRQs.

Try these sample practice questions with detailed answer explanations:

Differentiation: Composite, Implicit, and Inverse Functions Practice Tests

Question

If $f ((x)) = cos ((x^{2} - \frac{3 π}{2}))$ , then $f^{'} ((\sqrt{3 π)}) =$

	A. $- 2 \sqrt{3 π}$
	B. $- sin ((2 \sqrt{3 π)})$
	C. $1$
	D. $2 \sqrt{3 π}$

Hint :

Use the chain rule to differentiate a composite function.

Explanation

To find f^′(c), the value of the derivative of a function f at x = c, first differentiate f and then plug x = c into f^′(x).

The given function $f ((x)) = cos ((x^{2} - \frac{3 π}{2}))$ is a composite function of the form cos u, where $u = x^{2} - \frac{3 π}{2}$ is the inside function.

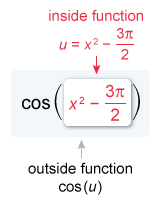
To find the derivative of a function of the form cos u, use the chain rule.

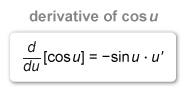
First differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x.

$f (x) = \cos (x^{2} - \frac{3 π}{2})$	Given function
$f^{'} ((x)) = - sin ((x^{2} - \frac{3 π}{2})) \cdot \frac{d}{dx} ((x^{2} - \frac{3 π}{2}))$	Apply chain rule
$f^{'} ((x)) = - sin ((x^{2} - \frac{3 π}{2})) ((2 x))$	Differentiate

To evaluate $f^{'} ((\sqrt{3 π}))$ , plug $x = \sqrt{3 π}$ into $f^{'} ((x))$ and simplify the result.

$f^{'} (x) = - \sin (x^{2} - \frac{3 π}{2}) (2 x)$	Derivative of $f$
$f^{'} (\sqrt{3 π}) = - \sin ({(\sqrt{3 π})}^{2} - \frac{3 π}{2}) (2 \sqrt{3 π})$	Plug in $x = \sqrt{3 π}$
$f^{'} (\sqrt{3 π}) = - \sin (3 π - \frac{3 π}{2}) (2 \sqrt{3 π})$	Evaluate: ${((\sqrt{3 π}))}^{2} = 3 π$
$f^{'} (\sqrt{3 π}) = - \sin (\frac{3 π}{2}) (2 \sqrt{3 π})$	Simplify: $3 π - \frac{3 π}{2}$ $= \frac{6 π}{2} - \frac{3 π}{2}$
$f^{'} (\sqrt{3 π}) = 2 \sqrt{3 π}$	Evaluate: $sin ((\frac{3 π}{2})) = - 1$

Therefore, $f^{'} (\sqrt{3 π}) = 2 \sqrt{3 π}$ .

(Choice A) $- 2 \sqrt{3 π}$ may result from differentiating $\cos x$ incorrectly: $\frac{d}{d x} [\cos x] \neq \sin x$ .

(Choice B) $- \sin (2 \sqrt{3 π})$ may result from not using the chain rule: $\frac{d}{d x} [f (g (x))] \neq f^{'} (g^{'} (x))$ .

(Choice C) $1$ may result from not using the chain rule: $\frac{d}{d x} [f (g (x))] \neq f^{'} (g (x))$ .

Things to remember:

To find the derivative of a composite function, use the chain rule:

\frac{d}{d x} [f (u (x))] = f^{'} (u (x)) \cdot u^{'} (x)

Question

If $y = 2 sin x - e^{3 x}$ , then $\frac{d^{3} y}{d x^{3}} =$

	A. 2 cos x − 3e^3x
	B. −2 sin x − 9e^3x
	C. −2 cos x − e^3x
	D. −2 cos x − 27e^3x

Hint :

The notation $\frac{d^{3} y}{d x^{3}}$ represents the third derivative of y with respect to x.

Explanation

The notation $\frac{d^{3} y}{d x^{3}}$ represents the third derivative of y with respect to x. To find the third derivative:

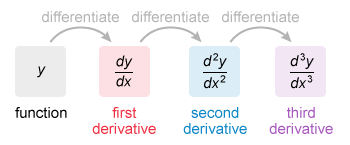
Differentiate each term of the given function y = 2sinx − e^3x to find the first derivative.

Use trigonometric differentiation rules to differentiate the first term. The second term is a composite function of the form e^u where u = 3x, so use the exponential chain rule to differentiate.

$y = 2 \sin x - e^{3 x}$	Given function
$\frac{dy}{dx} = 2 cos x - e^{3 x}$	Apply constant and trigonometric rules to differentiate first term
$\frac{dy}{dx} = 2 cos x - 3 e^{3 x}$	Differentiate second term

To find the second derivative, differentiate the first derivative.

$\frac{d y}{d x} = 2 \cos x - 3 e^{3 x}$	First derivative
$\frac{d^{2} y}{d x^{2}} = - 2 sin x - 3 e^{3 x}$	Apply constant and trigonometric rules to differentiate first term
$\frac{d^{2} y}{d x^{2}} = - 2 sin x - 3 e^{3 x} \cdot 3$	Apply constant and exponential rules to differentiate second term
$\frac{d^{2} y}{d x^{2}} = - 2 sin x - 9 e^{3 x}$	Simplify

Now differentiate the second derivative to find the third derivative.

$\frac{d^{2} y}{d x^{2}} = - 2 \sin x - 9 e^{3 x}$	Second derivative
$\frac{d^{3} y}{d x^{3}} = - 2 cos x - 9 e^{3 x}$	Apply constant and trigonometric rules to differentiate first term
$\frac{d^{3} y}{d x^{3}} = - 2 cos x - 9 e^{3 x} \cdot 3$	Apply constant and exponential rules to differentiate second term
$\frac{d^{3} y}{d x^{3}} = - 2 cos x - 27 e^{3 x}$	Simplify

Therefore, the third derivative of y = 2 sin x − e^3x is $- 2 cos x - 27 e^{3 x} .$ .

(Choice A) 2 cosx − 3e^3x is the first derivative of 2sinx − e^3x, but the question asks for the third derivative.

(Choice B) −2sinx − 9e^3x is the second derivative of 2sinx − e^3x, but the question asks for the third derivative.

(Choice C) $- 2 \cos x - e^{3 x}$ may result from not applying the chain rule to differentiate the second term.

Things to remember:

The notation $\frac{d^{3} y}{d x^{3}}$ represents the third derivative of y with respect to x.
To find the derivative of a composite function, use the chain rule.

Question

The table above gives selected values for a differentiable and increasing function g and its derivative. If g⁻¹ is the inverse function of g, what is the value of (g⁻¹)′(4) ?

	A. $- 5$
	B. $- 3$
	C. $\frac{1}{2}$
	D. $\frac{1}{5}$

Hint :

If g^-1 is the inverse of the function g, then the derivative of g^-1 at the point (a, b) is the reciprocal of the derivative of g at the point (b, a).

Explanation

If g⁻¹ is the inverse of the function g, then the derivative of g⁻¹ at the point (a, b) is the reciprocal of the derivative of g at the point (b, a):

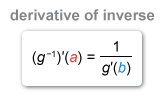
To find (g⁻¹)′(4), first use the table to find the value of x for which g(x) = 4. The table shows that g contains the ordered pair (−1, 4), so it's inverse g⁻¹ must contain the ordered pair (4, −1).

Plug a = 4 an b = −1 into the equation above, and then identify and plug in the value of gʹ(−1) from the given table.

${(g^{- 1})}^{'} (a) = \frac{1}{g^{'} (b)}$	Derivative of the inverse of g
${(g^{- 1})}^{'} (4) = \frac{1}{g^{'} (- 1)}$	Plug in a=4 and b=-1
${(g^{- 1})}^{'} (4) = \frac{1}{2}$	Plug in g'(-1)=2

Therefore, the value of ${(g^{- 1})}^{'} (4)$ is $\frac{1}{2}$ .

(Choice A) $- 5$ is the value of $g^{'} (4)$ , but the question asks for the value of ${(g^{- 1})}^{'} (4)$ .

(Choice B) $- 3$ is the value of $g^{'} (4)$ , but the question asks for the value of ${(g^{- 1})}^{'} (4)$ .

(Choice D) $\frac{1}{5}$ result from mistakenly taking the negative reciprocal of $g^{'} (4)$ , instead of the reciprocal of $g^{'} (- 1)$ , to calculate ${(g^{- 1})}^{'} (4)$ .

Things to remember:

If g^-1 is the inverse of the function g, then the derivative of g^-1 at the point (a, b) is the reciprocal of the derivative of g at the point (b, a).

{(g^{- 1})}^{'} (a) = \frac{1}{g^{'} (b)}

AP Calc Unit 3 on Your Fingers

No matter where you are, UWorld’s Mobile app ensures your preparation is always at your fingertips. From studying differentiation on the bus, watching a quick chain rule tutorial, or solving implicit differentiation MCQs, your AP Calc Unit 3 preparation never stops!

Stand Out
with a Top Score in AP Calculus AB

Finish your AP Calculus AB Unit 3 review and continue mastering all units with UWorld. Boost your performance and make yourself a standout candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription

Dream Score Plan

360-Day

^$169

Deep Learning Plan

180-Day

^$149

Score Booster Plan

90-Day (No print book, only digital)

^$129

Introductory Plan

30-Day (No print book, only digital)

^$99

Buy Now!

Get our all-in-one course today!

Focused AP Calc AB Videos
Print & Digital Study Guide
1400+ Exam-style Practice Questions
Customizable Quiz Generator
Adjustable Study Planner
Realistic Timed Test Simulation
Colorful Visual Explanations
Progress Dashboard
Smart Flashcards & Digital Notebook

Explore our free trial and frequently asked questions.

7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.

Frequently Asked Questions (FAQs)

What are the main topics covered in AP Calculus AB Unit 3: Differentiation: Composite, Implicit, and Inverse Functions?

AP Calculus AB Unit 3 covers advanced differentiation techniques, specifically the chain rule, implicit differentiation, and inverse function derivatives. It’s where calculus transitions from simple formulas to multi-layered problem solving. You’ll learn how derivatives describe relationships between intertwined functions, and how to apply them in equations where y isn’t isolated.

Core topics include:

Chain rule for differentiating composite functions
Implicit Differentiation
Differentiation of general and particular inverse functions
Determining higher-order derivatives of functions

This unit connects abstract calculus to practical reasoning, appearing heavily in Unit 3 progress check MCQs and FRQs. Mastering Unit 3 will strengthen the foundation for later topics, like motion, optimization, and integration, which depend on understanding composite relationships and implicit reasoning within derivative contexts.

How should I prepare for an AP Calculus AB Unit 3 exam?

Success in AP Calculus AB Unit 3 depends on balancing conceptual understanding with consistent practice. It’s not just about memorizing formulas but knowing when and how to apply them. To prepare effectively, approach each concept with purpose, clarity, and repetition.

Here’s what our experts recommend:

Start with UWorld’s composite, implicit, and inverse differentiation video lessons
Take handwritten notes by writing formulas like the chain rule by hand for memory retention
Practice Unit 3 progress check MCQs to test your recall under exam-style pressure
Solve FRQs weekly, focusing on step-by-step justification, not just final answers
Review detailed explanations after every practice session to understand your mistakes

Remember, AP graders reward reasoning as much as accuracy. In implicit differentiation, showing how dy/dx is derived earns partial credit even if the final value slips.

Are any free resources available for AP Calculus AB Unit 3?

Yes. UWorld offers a 7-day free trial that gives you access to AP Calculus AB Unit 3 lessons, practice questions, and study materials designed to strengthen your understanding of composite, implicit, and inverse differentiation. During this trial, you can explore interactive video lessons that visually break down key topics like the Chain Rule and Implicit Differentiation, as well as detailed explanations for every question.

Each problem includes step-by-step reasoning that helps you understand why certain approaches work and how to avoid common errors. You’ll also get access to sample Unit 3 progress check MCQs and FRQs modeled after the official AP exam. This trial period allows students to experience UWorld’s teaching approach, combining visual learning, structured explanations, and exam-style practice before committing to the full course. For students starting their AP Calculus AB Unit 3 review, these free resources are a smart way to build confidence and evaluate your current level of understanding.

What types of questions are on the AP Calculus AB Unit 3 test?

The AP Calculus AB Unit 3 test features multiple-choice and free-response questions that test your ability to apply differentiation techniques in various contexts. You can expect problems involving the Chain Rule, Implicit Differentiation, and Inverse Function Derivatives, often embedded in equations where variables interact or functions are nested.

In the MCQs, you might calculate dy/dx for an implicit relation, identify which differentiation rule applies, or evaluate a derivative at a specific point. FRQs, on the other hand, require a complete demonstration of reasoning, showing how to set up equations, differentiate correctly, and interpret results. The Unit 3 progress check MCQs and FRQs are designed in the same style as the official AP exam, making them an ideal resource for targeted practice. By regularly solving problems and reviewing detailed explanations, you’ll develop speed and clarity in handling complex differentiation questions.

How can I improve my score on the Free-Response Questions (FRQs) for Unit 3?

Improving your FRQ AP Calculus AB Unit 3 performance begins with structured reasoning and precise communication. The key is showing your process, not just the answer. AP Graders give credit for correct methods, clear notation, and logical justification, even if minor algebra errors occur.

To score higher:

Write complete solutions, and define all variables before differentiating
Label derivatives for clarity
Use proper notation in Chain and Implicit Differentiation
Interpret your results and don’t just compute
Review past FRQs to understand how scoring guidelines reward justification.

UWorld’s FRQ examples train you to think like a grader and anticipate what needs explanation. Over time, you’ll internalize strong habits: starting each response with the given, applying the derivative rule carefully, and concluding with a clear, contextual statement. The goal isn’t speed but structured precision that reflects genuine understanding.

What is the "Differentiation: Composite, Implicit, and Inverse Functions" unit's weight on the AP Calculus AB exam?

Unit 3 accounts for roughly 9-13% of the AP Calculus AB exam, but its influence extends far beyond that percentage. This unit introduces the most essential differentiation techniques, Chain Rule, Implicit Differentiation, and Inverse Function Derivatives, foundational to understanding later units on motion, optimization, and integration.

You’ll see them embedded within Unit 4 motion problems, Unit 5 related rates, and Unit 6 integration by substitution. Mastering these topics early gives you a significant advantage in all subsequent units. The College Board includes FRQs and MCQs that assess your ability to apply these derivative techniques in contextual scenarios, making Unit 3 one of the most skill-intensive sections of the course. Viewing this unit as your “differentiation foundation” ensures long-term payoff across the AP Calculus AB curriculum.

Where can I find a good study guide for AP Calculus AB Unit 3?

The ideal AP Calculus AB Unit 3 study guide transforms complex rules into understandable logic. UWorld’s interactive study guide helps you visualize the relationships between functions and their derivatives while reinforcing techniques through worked examples.

A strong Unit 3 study guide should include:

Clear, step-by-step explanations with layered examples
Visual representations
Practice problems that mirror Unit 3 progress check MCQs
Error analysis sections explaining why common mistakes occur
Quick-reference formula sheets to simplify revision

The UWorld study guide uses vivid diagrams, concise summaries, and real AP problem breakdowns to build intuitive understanding. Combined with lesson videos and progress check-style tests, it becomes an end-to-end prep solution that ensures you fully grasp composite, implicit, and inverse differentiation before test day.

Can I find practice tests specifically for AP Calc AB Unit 3?

Yes. UWorld offers specialized AP Calculus AB Unit 3 practice tests designed to match the exact tone, rigor, and structure of the official AP exam. These targeted practice sets focus on the repetition and variety needed to build mastery. Each test contains a mix of multiple-choice and free-response problems that emphasize both procedural fluency and conceptual understanding.

Every solution includes an in-depth explanation with mathematical reasoning, clarifying the correct answer and why it’s correct. By consistently working through these Unit 3 practice tests, you’ll learn to navigate the AP exam’s precise wording, avoid common mistakes, and approach each differentiation problem confidently and quickly. This focused preparation makes transitioning to full-length AP Calculus AB tests much smoother.