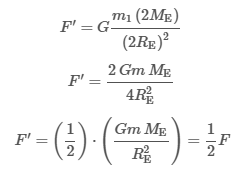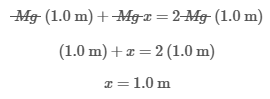AP® Physics 1 Practice Tests & Questions
Ace the AP® Physics 1 test with expertly crafted practice exams, sample tests, and practice problems from our Question Bank (QBank). With 450+ realistic AP Physics 1 questions and detailed explanations, you’ll master concepts faster and earn college credit on your schedule and budget.
Access Includes
- 450+ AP Physics 1 Practice Questions
- Customizable Quiz Generator
- Realistic Timed Physics 1 practice exam Simulation
- Colorful Visual Explanations
- Step-by-Step Solutions
- Adjustable Smart Study Planner
- Progress Dashboard
- Smart Flashcards
Try These AP Physics 1 Practice Questions
Kinematics Practice Test
Passage
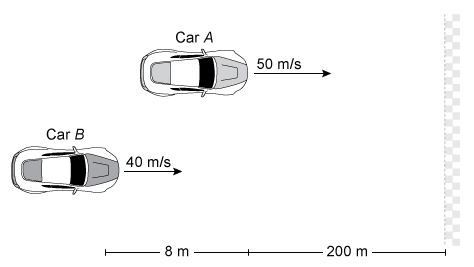
Two race cars approach the finish line of a race, as shown in the figure above. Cars A and B travel with speeds of 50 m/s and 40 m/s, respectively. At the instant shown, car A is 200 m from the finish line and car B is 8 m behind car A.
Question
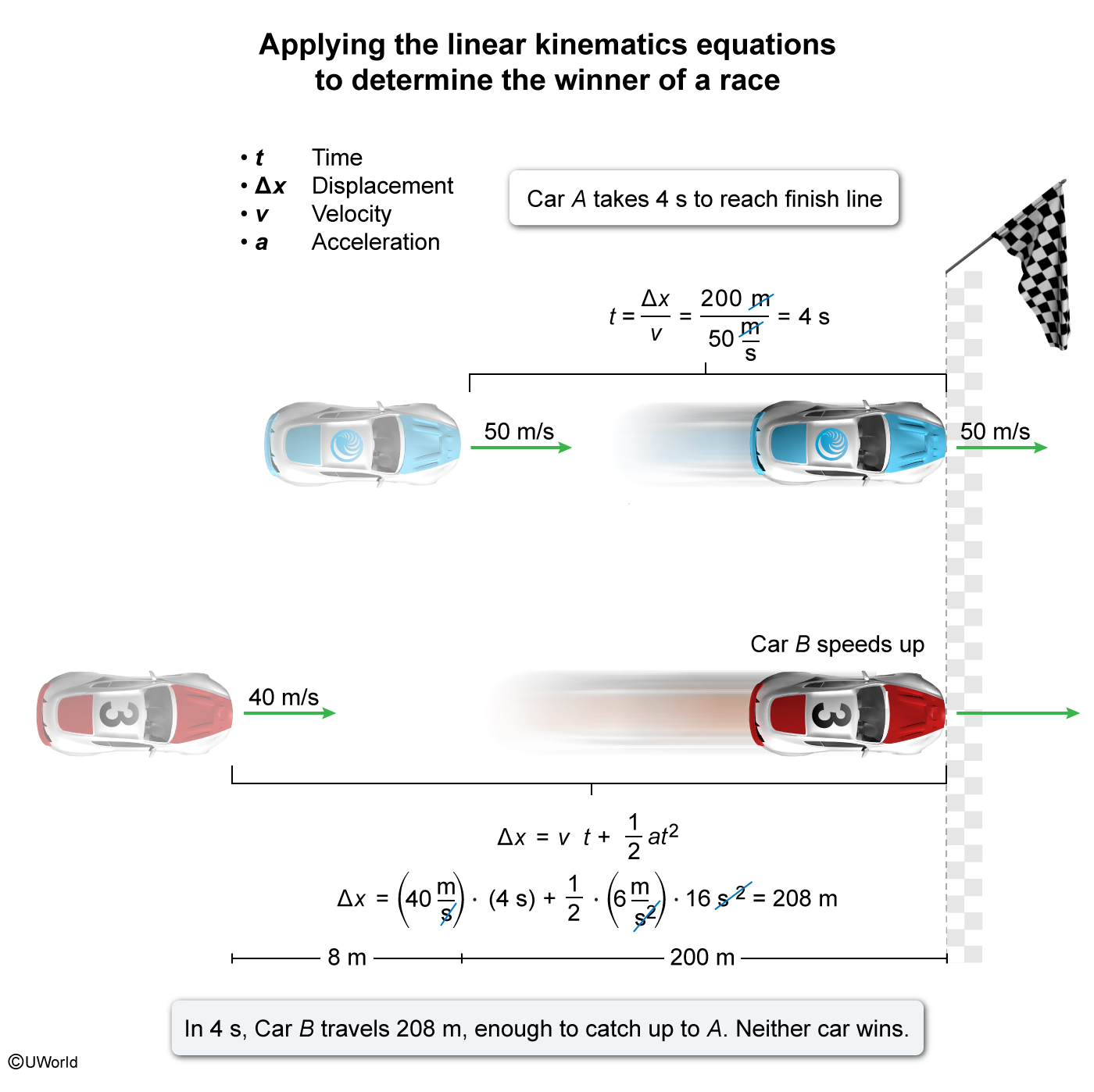
Car A continues to travel at 50 m/s toward the finish line, but car B begins to speed up with a constant acceleration of 6 m/s2. Which car wins the race?
| A. Car A | |
| B. Car B | |
| C.The car with the greatest speed at the finish line | |
| D. Neither; both cars reach the finish line at the same time |
Explanation
The position x and velocity v of an object experiencing a constant acceleration a are related through linear kinematics equations. Moreover, the displacement Δx (ie, the change in the object's position) equals the product of the initial velocity vi and the time t summed together with one-half the product of a and t2:
In this question, car A approaches the finish line at a constant speed of 50 m/s, so its acceleration is zero (a = 0). Consequently, the time it takes for car A to travel the 200 m to the finish line equals the ratio of Δx and vi:
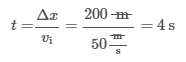
During the same 4 s interval, car B has a constant acceleration of 6 m/s2. Inserting t = 4 s, the acceleration a = 6 m/s2, and car B's initial velocity vi = 40 m/s into the linear kinematics equation yields:
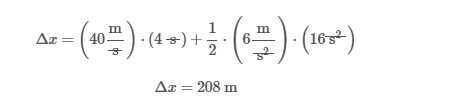
Because car B was initially 8 m behind car A, car B was initially a total of 208 m from the finish line. However, in the 4 s interval car B was able to gain ground and catch up to car A. Therefore, neither car wins the race because both reach the finish line at the same time.
(Choice A) Although car A has a greater initial velocity and is ahead of car B, car B catches up by accelerating.
(Choice B) This result follows from an error in applying the linear kinematics equation, such as forgetting the factor of one half in the second term of the equation.
(Choice C) Car B has a greater speed than car A at the finish line, but both cars reach the finish line at the same time.
Things to remember:
The displacement of an object undergoing a constant
acceleration can be determined from the linear kinematics equations.
Passage
Two race cars approach the finish line of a race, as shown in the figure above. Cars A and B travel with speeds of 50 m/s and 40 m/s, respectively. At the instant shown, car A is 200 m from the finish line and car B is 8 m behind car A.
Question
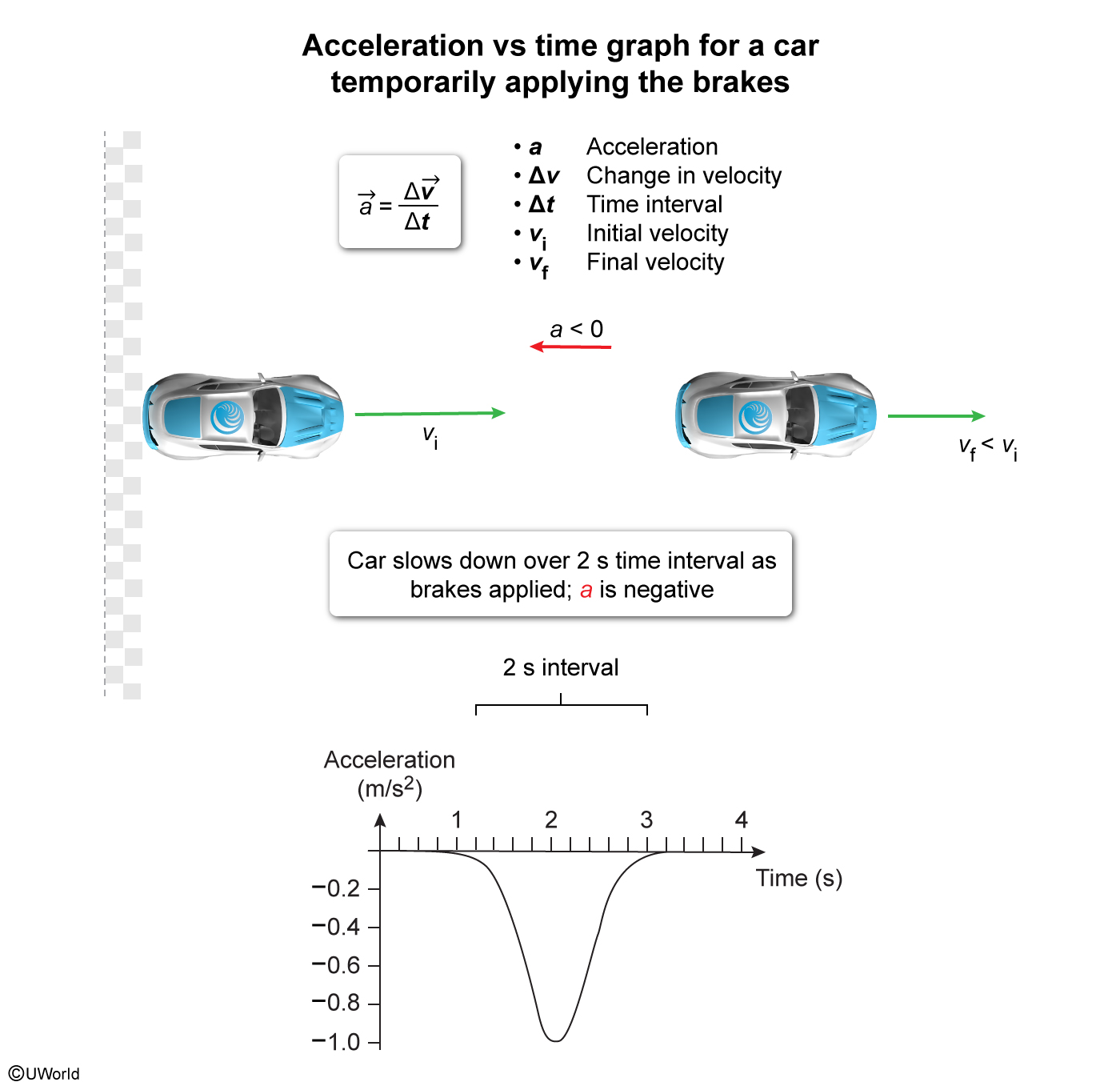
After crossing the finish line, the driver of car A steps on the brakes for 2 s and then releases them. Which of the following graphs best represents car A's acceleration as a function of time?
A. 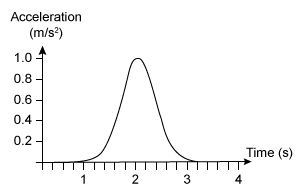
|
|
B. 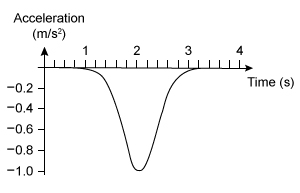
|
|
C. 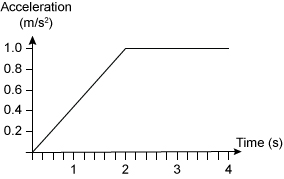
|
|
D. 
|
Explanation
The acceleration a of an object is a vector quantity that equals the change in the object's velocity Δv over an interval Δt:
In this question, car A moves in one dimension (ie, horizontally to the right). When the driver steps on the brakes for 2 s after crossing the finish line, the car slows down. Consequently, the car's final velocity vf is less than the car's initial velocity vi, and both Δv and a are negative:
When the driver releases the brakes, the acceleration becomes zero and the car again moves at a constant velocity. Because the acceleration becomes negative for an interval of 2 s and then returns to zero, the graph shown in Choice B best represents the acceleration of the car as a function of time.
(Choice A) This graph has the right shape but because the acceleration is positive, it corresponds to the driver stepping on the gas for 2 s, not hitting the brakes.
(Choices C and D) In these graphs, the acceleration increases (or decreases) from zero for 2 s, but after 2 s the acceleration remains constant. This behavior is inconsistent with the driver releasing the brakes and the acceleration returning to zero.
Things to remember:
Acceleration equals the change in velocity over time. An object that is slowing down experiences a negative acceleration.
Question
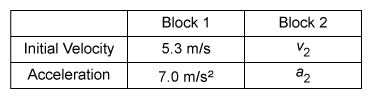
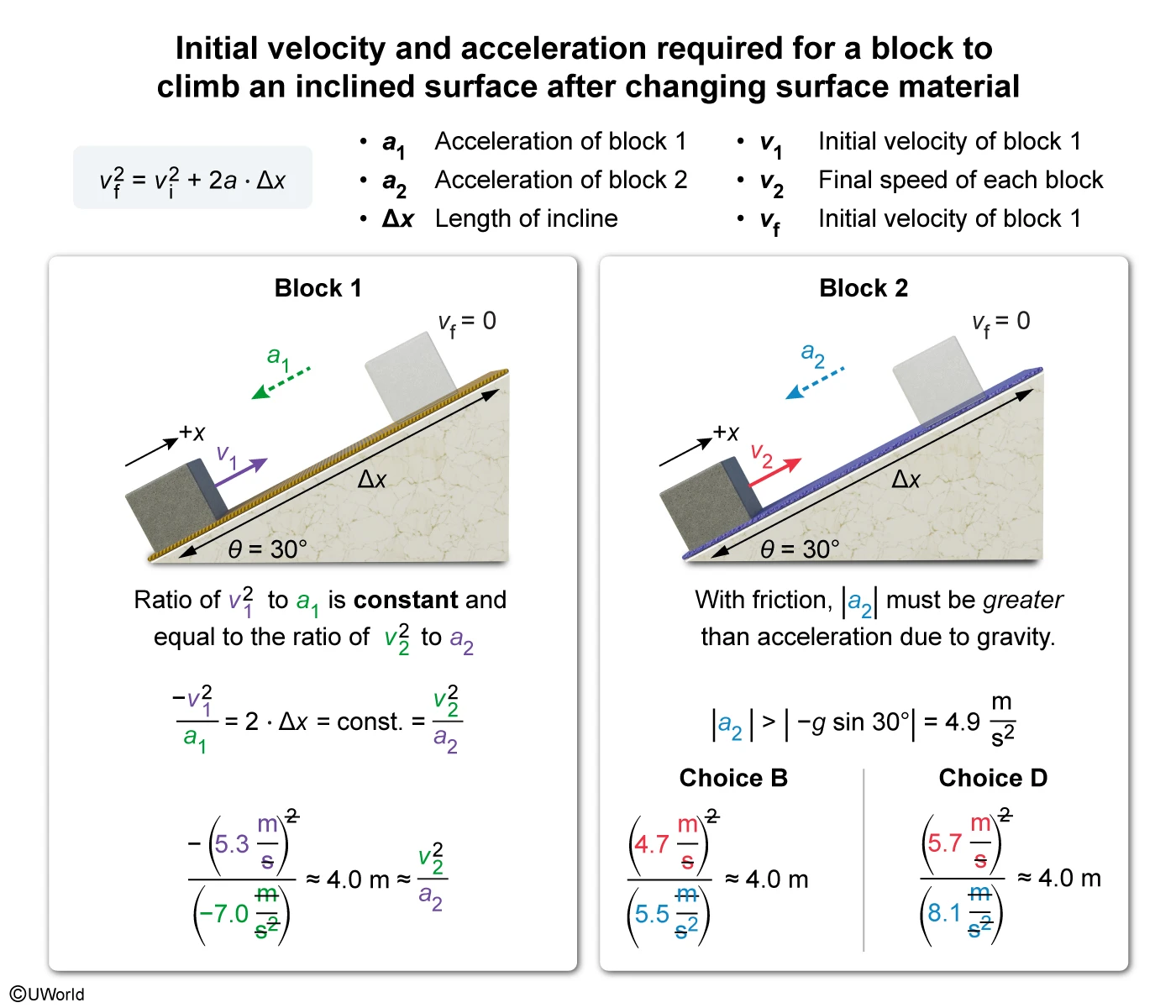
The data in the table above was recorded during an experiment in which two blocks were projected up a rough surface inclined at 30˚. After the launch of block 1, the rough material of the surface was changed to a different rough material. Both blocks began at the bottom of the incline and covered the same distance before coming to rest. What are the possible magnitude values of v2 and a2 of block 2? Select two answers.
A.
|
|||||
B.
|
|||||
C.
|
|||||
D.
|
Explanation
The motion of an object in one dimension is described by its position x, velocity v, and acceleration a. Acceleration is a vector quantity and is defined as the change in velocity Δv over an interval t. In cases where a is constant, Δx and the Δv (from initial v i to final v f), and t are related via the linear kinematic equations:
In this question, each block covers the same displacement Δx with different accelerations. Hence, each block requires a different initial velocity to reach the top. The equation relating v i, v f, a, and Δx is:
The vf in each case is zero, as the blocks come to rest at the top of the incline. Rearranging the equation yields:
Consequently, the ratio of the square of vi to a is always constant for the same length Δx. Thus, a proportionality can be established:
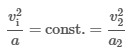
Substituting the values from the table yields the constant:
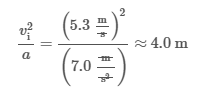
Thus, the ratio of vi2 to a must be approximately equal to 4.0 m (i.e., Δx is 2.0 m). Furthermore, because friction acts against the block's motion, the magnitude of a must be greater than the component of gravitational acceleration, which also acts against the block’s motion:
With Choice A eliminated (), the ratios can be calculated for B, C, and D:
Therefore, the possible values for v₂ and a₂ are those listed in Choice B and Choice D.
(Choice A) The ratio of to is correct in Choice A, but the acceleration cannot be less than that provided by gravity (4.9 m/s²).
(Choice C) The ratio of to must be approximately equal to 4.0 to traverse the entire incline.
Things to remember:
The constant acceleration of a moving object can be calculated from the linear kinematics equations
given information about the changes in the object's position and/or velocity over a time interval.
Dynamics Practice Test
Question
A rock climber has suspended herself within a narrow crevice by pressing her hands and feet outward against the walls such that she is not slipping. Which of the following statements are true about the forces of friction and gravity on the climber? Select two answers.
| A. The force of friction and the force of gravity act in opposite directions. | |
| B. The force of gravity on the climber is greater in magnitude than the friction forces. | |
| C.The climber is in static equilibrium. | |
| D. The friction forces are greater in magnitude than the force of gravity on the climber. |
Explanation
According to Newton's second law of motion, the sum of the forces ΣF on an object equals the product of the object's mass m and acceleration a:
Moreover, for an object to be in static equilibrium, the net force on the object must equal zero and the object must be stationary:
In this question, the climber is not moving and thus is in static equilibrium. Consequently, the climber experiences a downward force of gravity (ie, weight W) in the vertical direction and an upward force of total static friction Ff, which is a force between objects that prevents them from sliding past one another.
Furthermore, static friction will always act in a direction that maintains static equilibrium. Therefore, the total force of friction and force of gravity act in opposite directions, and the climber is in static equilibrium.
(Choice B) If the force of gravity is greater in magnitude than the friction forces, then the climber will slide and move down. Consequently, the climber will no longer remain in static equilibrium.
(Choice D) Because the climber is not moving, the net force must be equal to zero. Hence, the forces must be equal in magnitude and opposite in direction.
Things to remember:
In static equilibrium, the sum of all forces acting on
the object is zero and the object is stationary.
Question
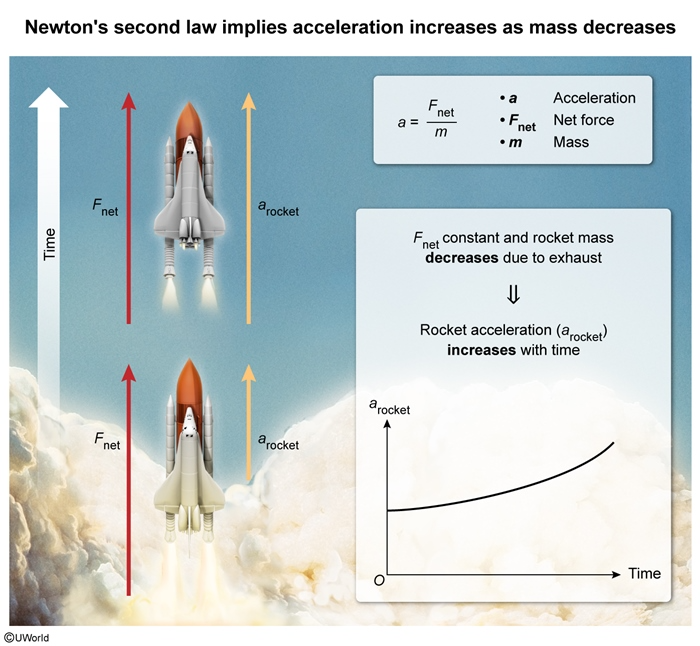
A rocket experiences a constant net force during its ascent. As it burns fuel, the rocket loses mass in the form of exhaust. Which of the following graphs best represents the acceleration arocket of the rocket as a function of time during its ascent?
A. 
|
|
B. 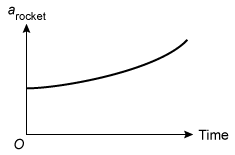
|
|
C. 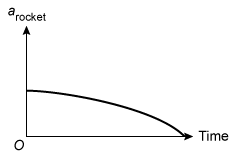
|
|
D. 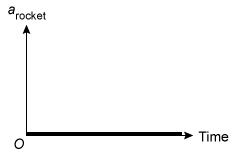
|
Explanation
Newton's second law of motion implies the acceleration (a) of an object is directly proportional to the net force Fnet exerted on the object and inversely proportional to the mass m of the object:
In this question, the rocket experiences a constant net force as it ascends, but it loses mass as fuel is burned and expelled as exhaust. Hence, the rocket's mass mrocket is decreasing with time. Because Newton's second law implies that acceleration is inversely proportional to mass, it follows that the rocket's acceleration arocket is an increasing function of time:
Therefore, Choice B is correct because it is the only graph that represents arocket as an increasing function of time.
(Choice A) The rocket's acceleration would be constant if the net force and the rocket mass are constant. However, the rocket's mass decreases and its acceleration increases.
(Choice C) As the mass of the rocket decreases, Newton's second law implies that its acceleration increases, not decreases.
(Choice D) Because the rocket experiences a non-zero net force, Newton's second law implies the acceleration of the rocket is not zero.
Things to remember:
An object's acceleration is directly proportional to the
net force applied and inversely proportional to the object's mass. For a constant net force,
decreasing the mass of an object will increase its acceleration.
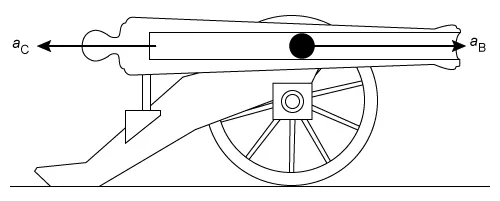
Question
During the process of firing, a cannon accelerates in one direction with a magnitude aC while the cannonball accelerates in the opposite direction with a magnitude of aB, as shown above. On which, if either, does the greater force act?
| A. The cannon | |
| B. The cannonball | |
| C.Neither; the forces acting on each are the same magnitude. | |
| D. The answer cannot be determined without knowing the masses of the cannon and cannonball. |
Explanation
A free-body diagram shows all external force vectors acting on an object or system. Newton's second law of motion implies that the acceleration a of an object is the ratio of the net force Fnet exerted on the object to the object's mass m:
Newton's third law of motion implies that forces arise from interactions. When object A exerts a force on object B, a reaction force equal in magnitude and opposite in direction is generated back on A by B:
In this question, the process of firing causes both cannon and cannonball to accelerate in opposite directions with magnitudes aC and aB, respectively. The interaction between the cannon and the cannonball produces one force on the cannonball and a second force of equal magnitude in the opposite direction on the cannon:
Furthermore, Newton's second law implies that for a given force on an object, the acceleration is inversely proportional to the object's mass:
Consequently, any difference in acceleration can be attributed to the difference in mass, not force. Therefore, although the cannon and cannonball have different masses and accelerations, the magnitude of the forces acting on the cannon and cannonball are the same.
(Choices A and B) The difference in acceleration between the cannon and cannonball is due to the difference in mass of the objects, not a difference in force acting on them. Newton's third law implies that the force on the cannon is equal in magnitude to the force on the cannonball.
(Choice D) Newton's third law implies that the magnitude of the forces on the cannon and cannonball are equal. The difference in acceleration is due to the difference in mass, not force.
Things to remember:
Newton's third law of motion implies that an interaction between two objects produces forces on each object of equal magnitude. Newton's second law of motion implies that the acceleration of an object is the ratio of net force to its mass.
Circular Motion and Gravitation Practice Test
Passage
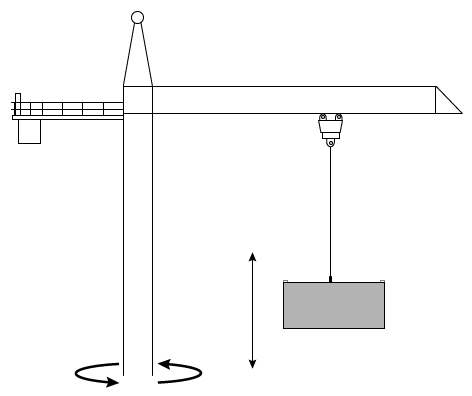
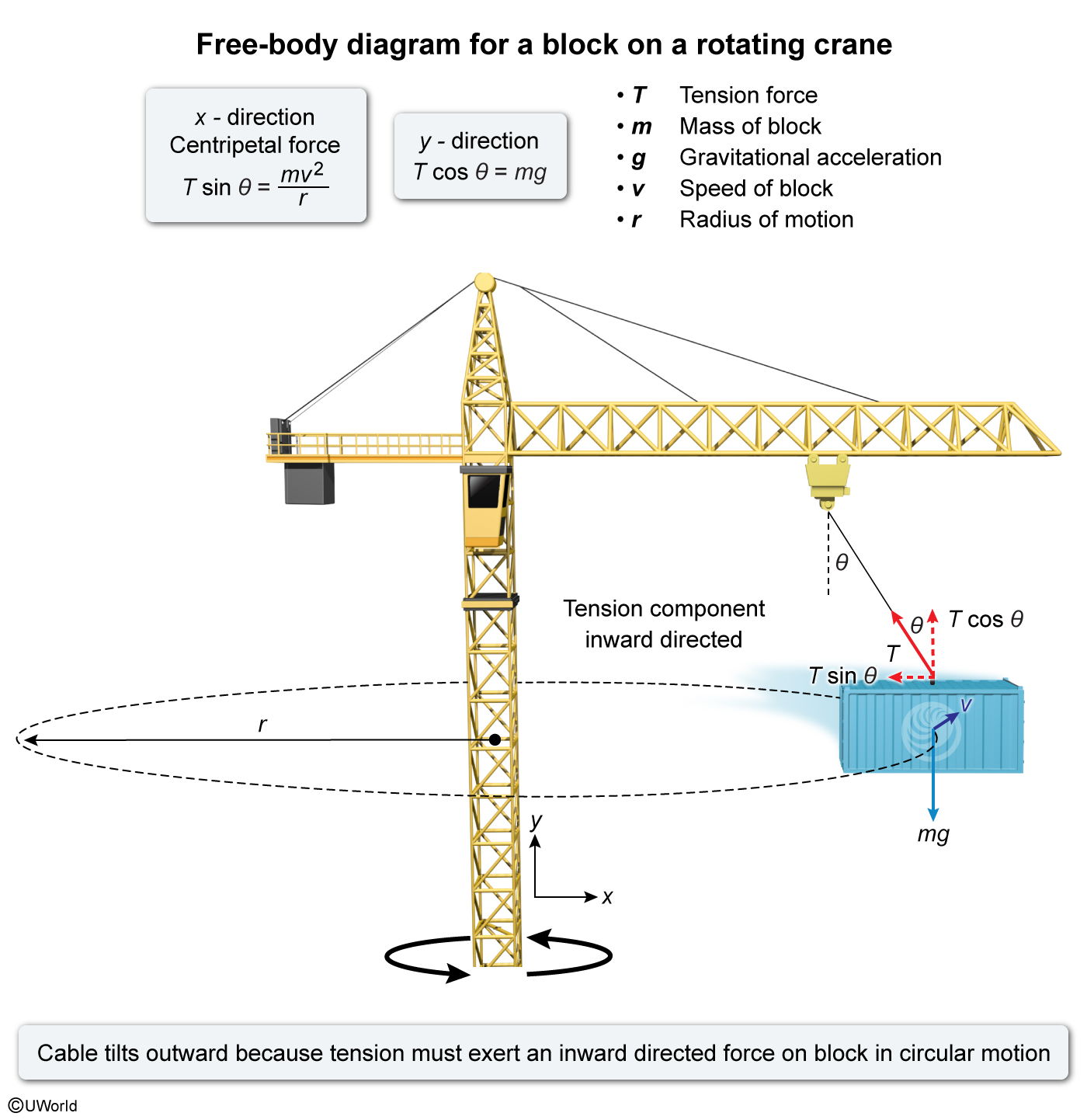
A building company uses a crane to raise and lower materials at a construction site. The cable near the end of the crane moves blocks up and down, and the crane can rotate about its central vertical axis, as shown in the diagram above.
Question
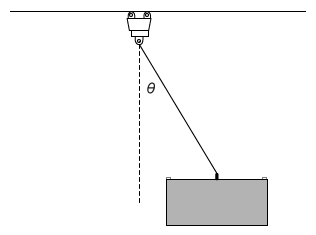
As the crane moves to reposition a block, it begins to rotate with a constant velocity about its vertical axis. As the crane rotates, the block and cable tilt outward with an angle θ, as shown above. Which of the following best explains why the block and cable tilt outward?
| A. As the block rotates in a circular path, the cable must exert an inwardly directed force on the block. | |
| B. As the block rotates in a circular path, the cable must exert an outwardly directed force on the block. | |
| C. As the block rotates in a circular path, there is an inwardly directed component of the gravitational force. | |
| D. As the block rotates in a circular path, there is an outwardly directed component of the gravitational force. |
Explanation
When an object moves in uniform circular motion, the magnitude of its velocity is constant but the direction of its velocity is constantly changing. Consequently, an object of mass m in uniform circular motion experiences a centripetal acceleration a c, and Newton's second law of motion implies there is a net centripetal force F c that equals the product of m and a c:
In this question, as the crane rotates the block moves at a constant velocity v in a circular path of radius r. Hence, a radial inwardly directed F c must be exerted on the block. F c equals the block's mass m multiplied by a c, which is also equal to the ratio of v 2 and r:
The behavior of the cable-block system can be analyzed by introducing an xy-coordinate system and constructing a free-body diagram showing the components of the forces in each direction. In this case, x is in the radial direction and y is vertically upward. The weight of the block is always directed vertically downward but because the block and cable tilt outward with angle θ, there are x- and y-components of the cable tension T.
In the y-direction, there is zero net force but in the x-direction, the net force equals F c. Resolving the tension in each direction yields:
Therefore, the cable and block must tilt outward so that the cable can exert an inwardly directed force on the block.
(Choice B) The net force on an object in uniform circular motion is directed radially inward, not radially outward.
(Choices C and D) The gravitational force on the block always points vertically downward, and therefore it exerts zero force in the radial direction.
Things to remember:
An object in uniform circular motion experiences a net inwardly
directed (centripetal) force. A free-body diagram can be used to visualize the centripetal force on an
object.
Question
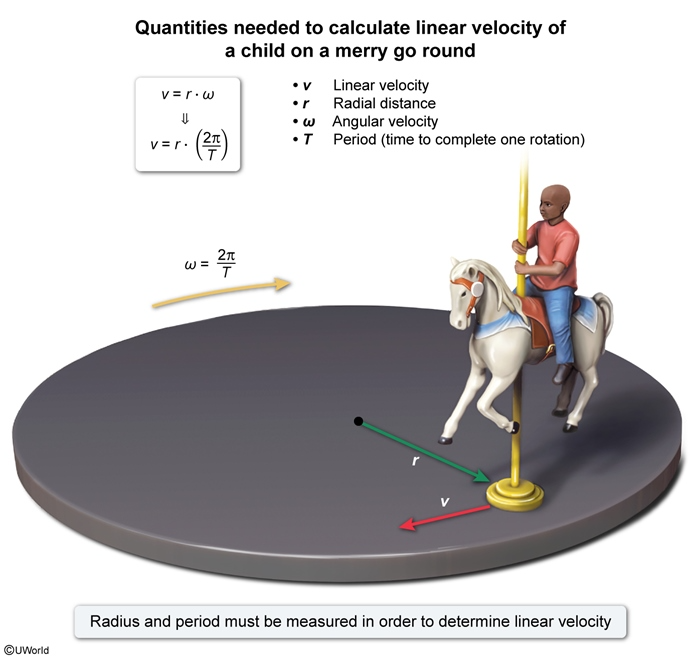
A student has been asked to determine an approximate value for the linear velocity of a child on a merry-go-round when it is rotating with an unknown, but constant angular velocity ω, as shown above. Which of the following quantities must be measured to determine the linear velocity? Select two answers.
| A. The period of rotation of the merry-go-round | |
| B. The mass of the child | |
| C. The radial distance of the child from the center of the merry-go-round | |
| D. The mass of the merry-go-round |
Explanation
The linear velocity of an object is equal to the change in the object's displacement Δx over a time interval Δt:
If the object is rotating in a circular path at a radial distance r from the axis of rotation, Δx equals the product of r and the angular displacement Δθ:
Substituting this equation into the velocity equation shows that v is the product of r and the angular velocity ω:
Furthermore, if the object is rotating at a constant angular velocity, then ω can be determined from the ratio of the angular displacement through one complete rotation (Δθ = 2π radians) and the time T to complete that rotation (ie, the period) Δt = T:
Consequently, linear velocity is:
which is the ratio of circumference 2πr to period. In this question, the student must determine the linear velocity of the child sitting on a merry-go-round rotating with constant angular velocity. The above equation for v therefore implies that the student must measure both the child's radial distance from the center r and the merry-go-round's period of motion T.
(Choices B and D) The mass of the child and the merry-go-round are unnecessary to determine the linear velocity of the child. Only the radius and the period are needed.
Things to remember:
The linear velocity of an object in uniform circular motion is the product of radius and angular velocity, which can be determined from the period of motion.
Question
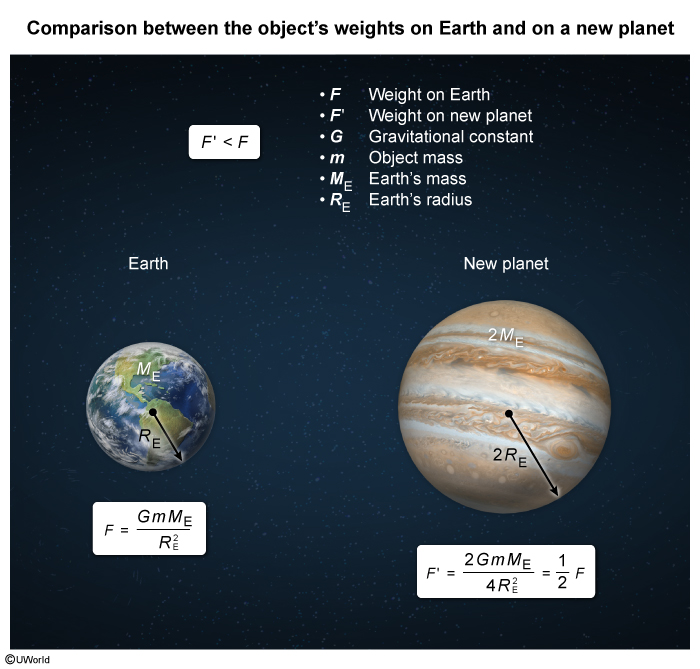
An object with weight F on Earth is moved to a planet that has twice the mass and twice the diameter of Earth. How does the magnitude of the object's weight F' on the new planet compare to that of the object's weight F on Earth?
| A. | |
| B. | |
| C. | |
| D. F′ can be greater or less than F, depending on the mass of the object. |
Explanation
According to Newton's law of universal gravitation, the strength of the gravitational field (g) created by an object of mass M is directly proportional to M and inversely proportional to the square of the distance r 2 from the center of mass of the object:
The universal gravitational constant G equals 6.67 × 10−11 m3 kg−1 s−2 . The gravitational force F g experienced by an object of mass m is equal to:
In this question, Earth has mass M E and radius R E, so the gravitational force (ie, weight) experienced by an object on Earth's surface is equal to:
On the new planet with mass 2M E (ie, twice the mass of Earth) and radius 2R E, the object will weigh F':
Consequently, the object will weigh half as much as it does on Earth, and therefore F' < F.
(Choice B) The larger diameter of the new planet more than compensates for the additional mass of the planet. Therefore, the object weighs less.
(Choice C) The object cannot weigh more because the larger radius of the new planet decreases the gravitational field strength by a factor of ¼ whereas the greater mass increases the gravitational field strength only by a factor of 2.
(Choice D) Although the mass of the object remains the same, it will weigh less on the new planet regardless of its mass.
Things to remember:
The gravitational field on the surface of a planet is
directly proportional to the planet's mass and inversely proportional to square of the planet's
radius. Changes in a planet's mass and radius can change the strength of the planet's
gravitational field.
Energy Practice Test
Question
A child slides down from the same height along three frictionless slides A, B, and C. Slide A is straight and slides B and C are curved, as shown above. The child reaches the bottom of slide B in less time than going down A or C. For which slide is the change in the gravitational potential of the child-Earth system the greatest?
| A. A | |
| B. B | |
| C. C | |
| D. The change in gravitational potential energy is the same for all slides. |
Explanation
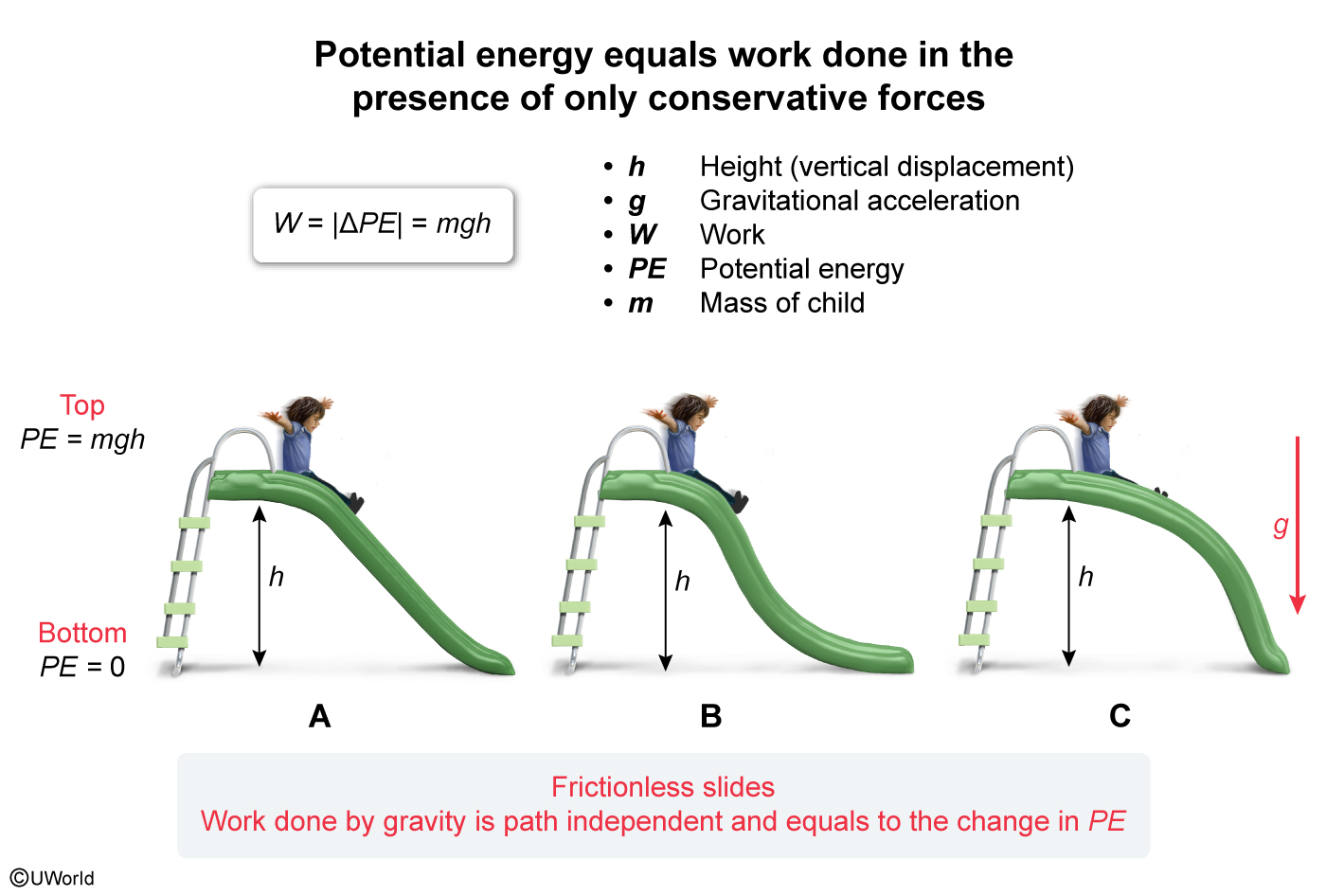
When an object is only subjected to conservative forces (eg, gravity), the work W done is independent of the path taken by the object as the force is applied. Consequently, the work done is equal to the negative of the change in the gravitational potential energy (PE):
The PE equals the product of mass m, height h, and gravitational acceleration g:
In this question, three frictionless slides with different path shapes are given, and gravity is the only force present that does work on the child. The path shape of each slide is not significant due to the absence of friction; the work done by gravity on the child is independent of the path and time taken, and equals the change in PE.
Furthermore, the child starts and ends at the same vertical position for each slide, so the value of h (vertical displacement) is the same for all three slides. Therefore, the child experiences the same change in gravitational PE on each slide.
(Choices A, B, and C) The child starts and ends at the same height for each slide. Therefore, gravitational PE is the same for all three slides.
Things to remember:
Work done on an object is independent of the path when the object is
subjected only to conservative forces. The change in gravitational potential energy depends only on
the vertical change in position, not on the path taken.
Passage
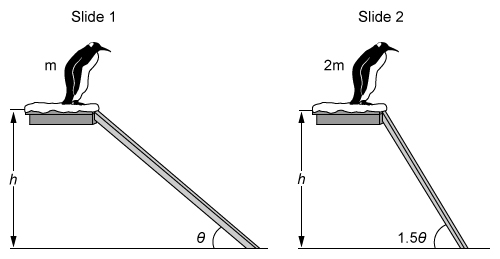
A penguin of mass m slides from rest down a frictionless slide of height h at an angle of θ with the ground. A second penguin of mass 2m slides from rest down a frictionless slide of the same height h, but at an angle of 1.5θ with the ground, as shown above.
Question
How does the kinetic energy of the two penguins at the ground compare, and why?
| A. The first penguin reaches the ground with a greater kinetic energy because Slide 1 is longer. | |
| B. The second penguin reaches the ground with a greater kinetic energy because the work done on the penguin is greater. | |
| C. The two penguins reach the ground with the same kinetic energy because the slides have the same vertical height. | |
| D. The two penguins reach the ground with the same kinetic energy because mechanical energy is conserved. |
Explanation
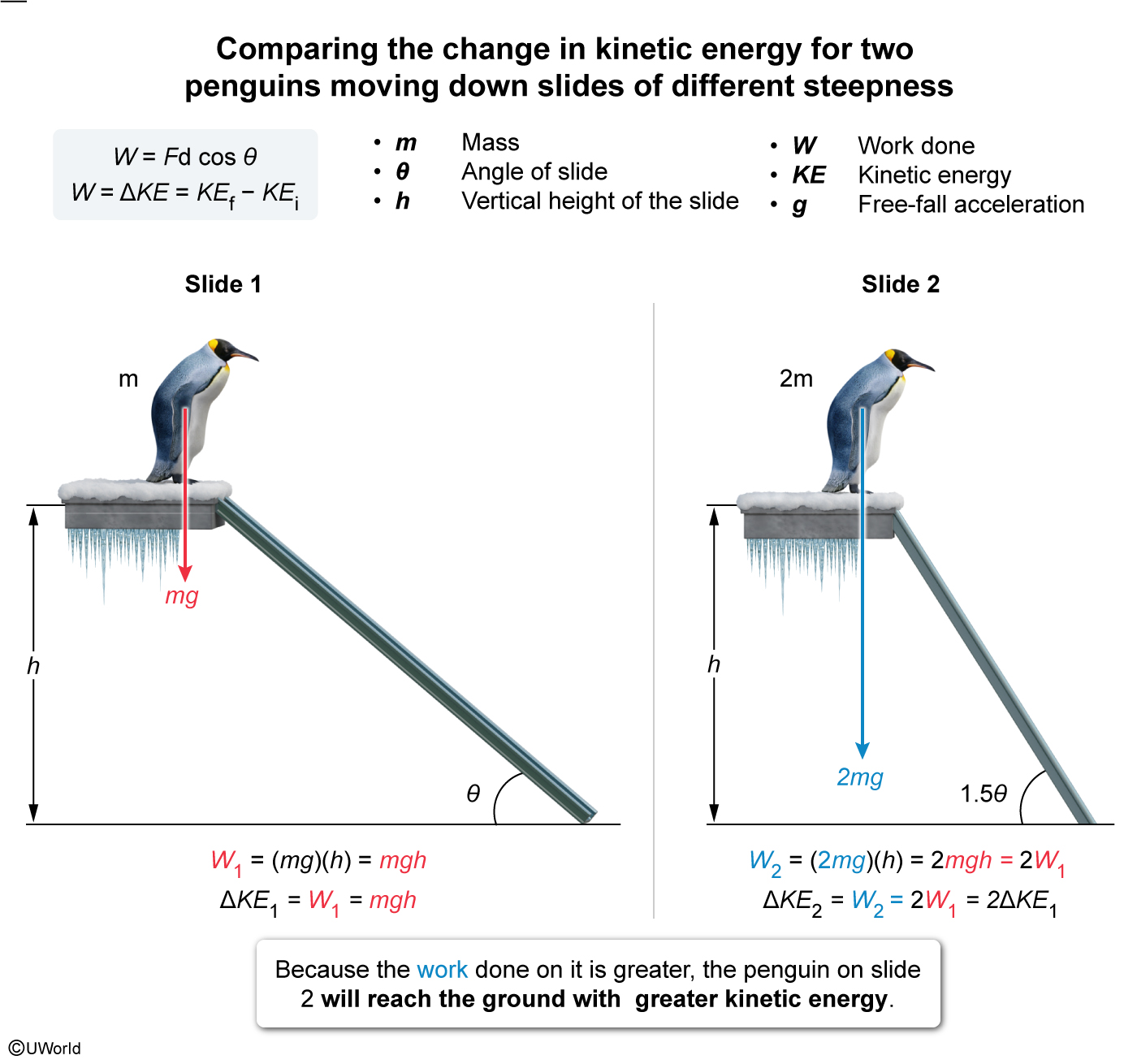
The work W done on an object is equal to the product of the magnitude of the force F exerted on the object, the magnitude of the object's displacement d, and the angle θ between the force and displacement vectors:
Furthermore, according to the work-energy theorem, the net work done W net on an object equals its change in kinetic energy ΔKE:
In addition, for conservative forces (eg, gravity), the work done is independent of the path the object takes as it moves between a final position x f and an initial position x i.
In this question, the downward gravitational force (ie, weight) mg is a conservative force that does work W 1 on the penguin moving a vertical distance h down slide 1:
Thus, the work done equals the change in kinetic energy ΔKE 1 of the penguin:
The work done W 2 on the penguin moving down the second slide is the product of the force 2mg and the same vertical distance h:
Therefore, because the work done on it is greater, the second penguin reaches the ground with a greater kinetic energy:
(Choice A) Slide 1 is longer, but ΔKE equals W net and the work done on the second penguin is greater because it has more mass.
(Choice C) The slides do descend the same vertical height h, but ΔKE equals W net and the work done on the second penguin is greater because it has more mass.
(Choice D) Mechanical energy is conserved, but the penguin with more mass undergoes a greater change in gravitational potential energy and experiences a greater change in kinetic energy.
Things to remember:
The work done on an object equals the product of force and
displacement. The work done by a conservative force (eg, gravity) is independent of the path the
object takes.
Question
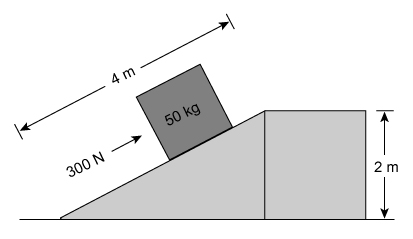
A student exerts a force of 300 N to push a box with mass 50 kg up a rough incline a distance of 4 m, as shown above. As a result of being pushed up the incline, the box is raised 2 m above the ground. Assuming the box begins and ends at rest, the work done by the force of friction in moving the box up the incline is most nearly
| A. −220 J | |
| B. 0 J | |
| C. 980 J | |
| D. 1,200 J |
Explanation
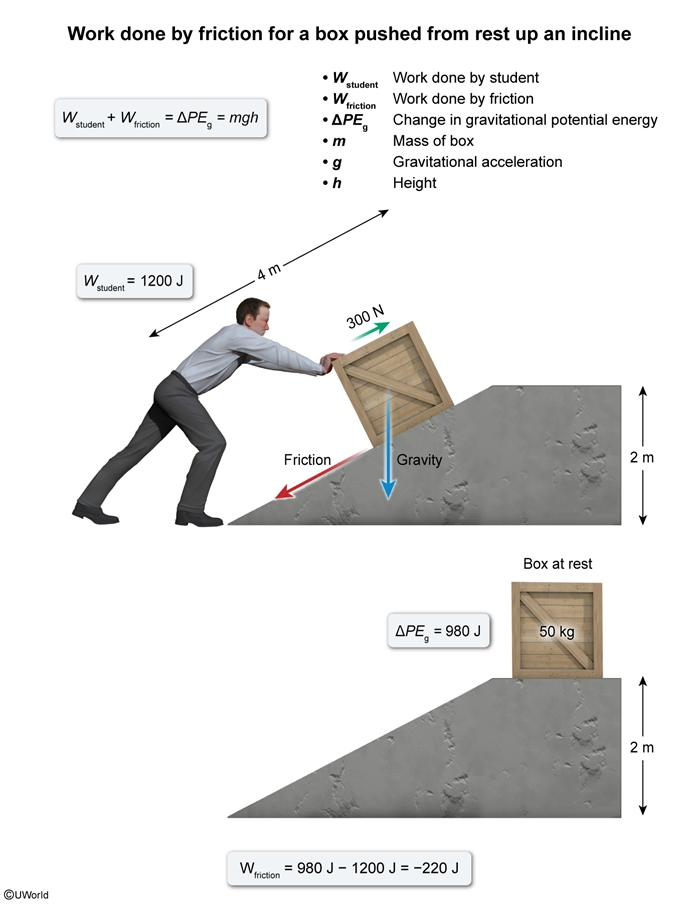
According to the work-energy theorem, the net work W net done on an object equals the change in the object's kinetic energy (ΔKE):
When both conservative forces (eg, gravity) and nonconservative forces (eg, friction) act on the object, the net work is the sum of the work done by the conservative forces W c and the work done by the nonconservative forces W nc:
Furthermore, the work done by conservative forces equals the negative of the change of the potential energy (ΔPE):
Inserting these equations into the work-energy theorem yields:
Hence, W nc equals the sum of ΔKE and ΔPE (ie, the change in the total mechanical energy):
In this question, two nonconservative forces (the pushing force of the student and the force of friction) do work on the box. In addition, the work done against gravity changes the system's gravitational potential energy (PE g) as the box is raised:
Substituting the height h = 2 m, box mass m = 50 kg, and gravitational acceleration g = 9.8 m/s2 yields:
Because the box begins and ends at rest, ΔKE = 0. Consequently,
The work done by the student is the product of the force magnitude and the distance up the incline:
Therefore, the work done by friction equals:
(Choice B) The change in the box's KE is zero, but the work done by friction is the difference between the change in PE and the work done by the student.
(Choices C and D) 980 J and 1,200 J are the work done against gravity and the work done by the student, respectively. However, the work done by friction is negative and equal to the difference of these two values.
Things to remember:
The work done by nonconservative forces equals the change in the
system's total mechanical energy.
Momentum Practice Test
Question
Some students release a bouncy ball from a known height above a flat, horizontal surface. The ball collides with the surface and bounces upward. Which of the following pieces of equipment would yield a measured quantity that would be enough to determine whether the ball's collision with the floor was elastic?
| A. Balance | |
| B. Meterstick | |
| C. Force sensor | |
| D. Spring scale |
Explanation
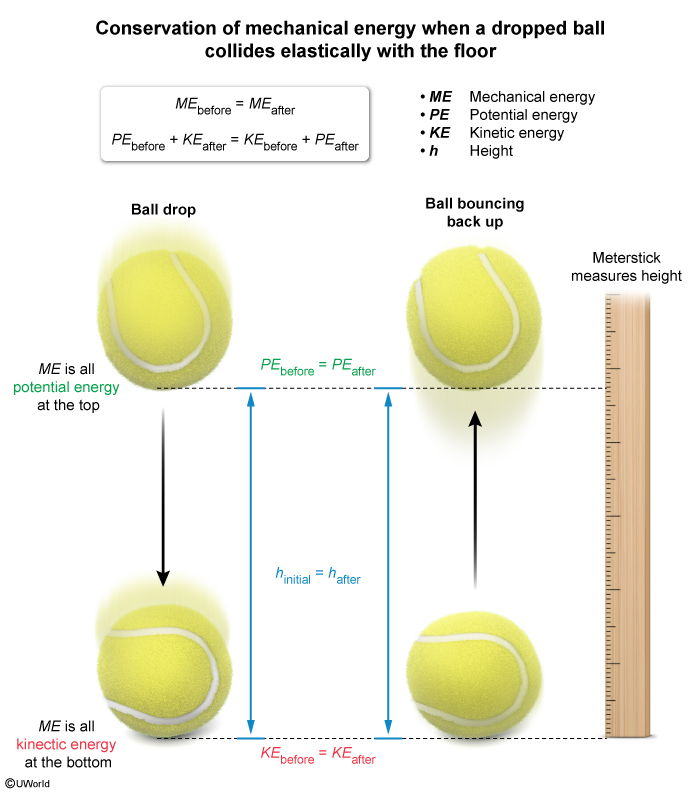
In an elastic collision, where colliding objects have very small interaction time and no energy is lost, the total kinetic energy (KE) is conserved:
In this question, a ball is dropped from a known initial height. The total mechanical energy of the ball is the sum of the ball's gravitational potential energy and kinetic energy at any point on the ball's path. The ball's mechanical energy is initially all in the form of potential energy. However, when the ball hits the floor, the mechanical energy has all transformed into kinetic energy.
If no energy is lost due to interaction between the ball and the floor, the collision is elastic. Hence, when the ball bounces upward, it has the same mechanical energy and bounces back to the same initial height.
If the final height is the same as the initial height, then mechanical energy is conserved and the collision is elastic. Therefore, using a meterstick to measure the final height of the ball after bouncing upward is the easiest method to determine if the collision is elastic.
(Choices A and D) A balance or a spring scale are used to measure the ball's mass. The ball's mass is constant during the collision and has no effect on any physical quantity afterward.
(Choice C) A force sensor (placed on the ground, under the ball) could aid in determining the speed (or kinetic energy) of the ball as it bounces upward, but only if the mass of the ball is known.
Things to remember:
In an elastic collision, no loss of mechanical energy is
observed during the collision (ie, total mechanical energy is conserved).
Question
A bowling ball with mass of m b moving at v b,i strikes a bowling pin with a smaller mass of m p, initially at rest. After the collision, the final velocity of the ball and pin are measured as v b,f and v p,f, respectively. Which of the following principles must be applied to determine whether the collision is elastic or inelastic, and why?
| A. Conservation of momentum, because Newton's third law of motion requires that the force the ball exerts on the pin is equal in magnitude to the force that the pin exerts on the ball. | |
| B. Conservation of momentum, because the impulse that the ball exerts on the pin is equal to the impulse that the pin exerts on the ball. | |
| C. Conservation of kinetic energy, because the ball transfers all its kinetic energy to the pin. | |
| D. Conservation of kinetic energy, because momentum is conserved in all collisions but kinetic energy is only conserved in elastic collisions. |
Explanation
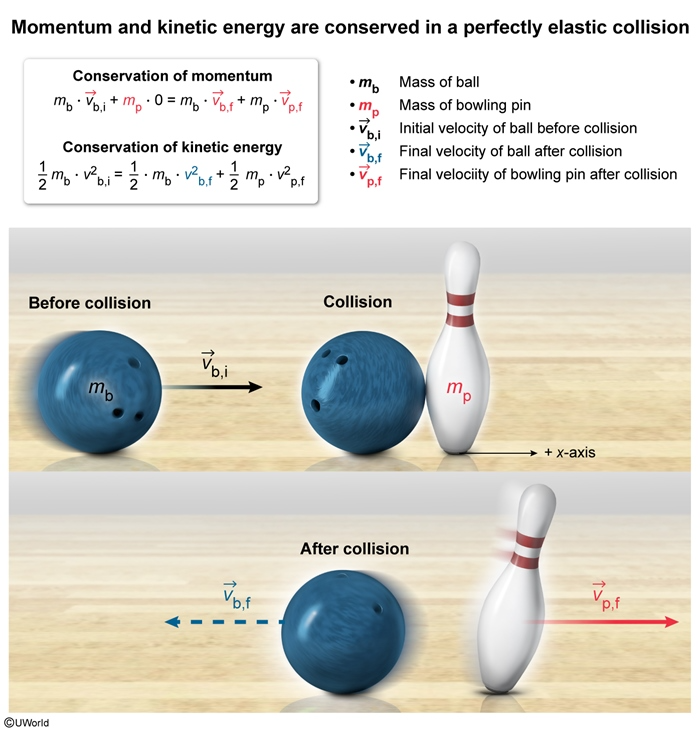
The momentum P of a moving object is equal to the object's mass m multiplied by its velocity v:
Newton's second law of motion implies that the change in momentum ΔP over a time interval Δt is equal to the net force F exerted on the object:
The change in momentum of an object (defined as the impulse, I) is
A collision, an interaction between two objects (e.g., A and B) over time, is governed by Newton's third law of motion, which states that interaction forces arise in equal and opposite pairs. Hence, the impulses exerted on each object are equal and opposite:
Consequently, the changes in momentum are equal and opposite, and total momentum is conserved in all collisions:
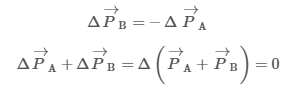
However, the type of collision dictates whether kinetic energy (KE) is conserved. In an elastic collision, no energy is lost due to the interaction of objects, and the kinetic energy of the objects before and after the collision are equal:
Therefore, momentum is conserved and only conservation of kinetic energy can be used to determine whether the collision between the bowling ball and the pin is elastic.
(Choices A and B) Momentum is conserved in all collisions, so the conservation of momentum cannot solely be used to determine the type of collision.
(Choice C) Kinetic energy is conserved in elastic collisions. However, it is not because all the ball's kinetic energy is transferred to the pin but because both objects' kinetic energy before and after the collision are equal.
Things to remember:
Total momentum is conserved in all collisions, both elastic and inelastic. Total kinetic energy is
conserved only in elastic collisions.
Question
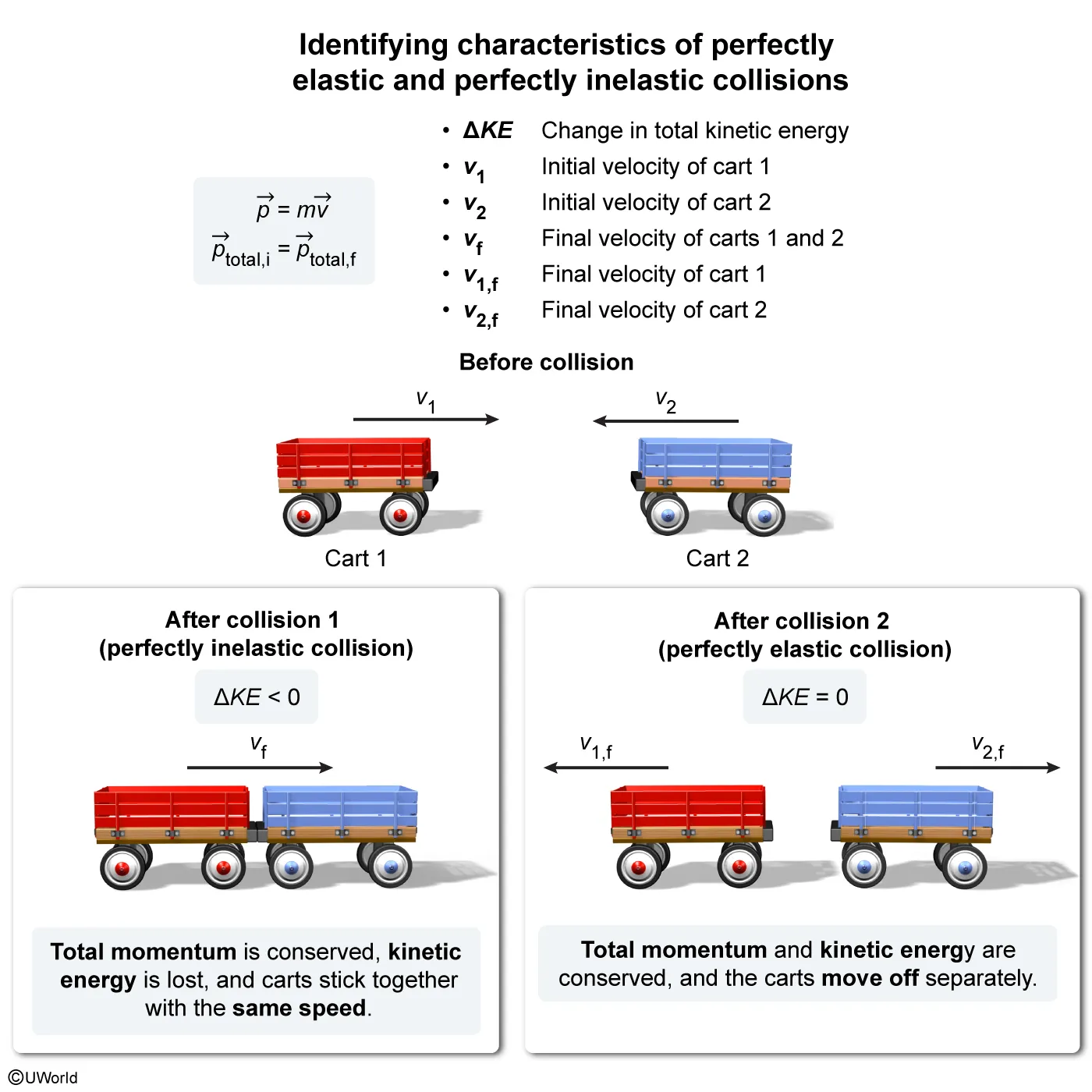
A student oversees two collisions in a lab setting. In collision 1, the two carts stick together in a perfectly inelastic collision. In collision 2, the same two carts exhibit a perfectly elastic collision. Which of the following statements about the collisions must be true? Select two answers.
| A. The final speed of each cart after the collision is the same in collision 1 but different in collision 2. | |
| B. The total momentum before and after collision 1 and collision 2 remains constant. | |
| C.The kinetic energy dissipated in collision 2 is greater than that in collision 1. | |
| D. The kinetic energy dissipated in collision 2 is equal to zero. |
Explanation
Momentum p is the product of the mass m and the velocity v of an object:
In a system of objects, the total momentum ptotal is defined as the sum of the individual momenta:
In a perfectly inelastic collision, two objects A and B moving in one dimension (ie, the x-direction) collide and stick together, moving as one object with the same final velocity vf. Because the forces of the collision are internal to the system, conservation of momentum implies that:
In a perfectly elastic collision, A and B collide and bounce off one another, moving off separately after the collision. Hence, no kinetic energy (KE) is lost in the collision, and the total KE of the system is conserved. Furthermore, conservation of momentum implies that:
Although total momentum is conserved in all collisions, the total kinetic energy of the system is not conserved (and some is dissipated) in an inelastic collision.
In this question, collision 1 is a perfectly inelastic collision and collision 2 is a perfectly elastic collision. Therefore, the total momentum is conserved in both collisions, and the kinetic energy dissipated in collision 2 equals zero.
(Choice A) Although the final speed of each cart after collision 1 must always be the same, the final speed of each cart after collision 2 could be the same under certain circumstances (and therefore not always different).
(Choice C) Kinetic energy is dissipated in inelastic collisions and conserved in perfectly elastic collisions. Hence, the kinetic energy dissipated in collision 1 is greater than that in collision 2.
Things to remember:
Momentum is conserved in collisions if no net external forces act on the system. In a perfectly inelastic collision, kinetic energy is dissipated, and the two objects stick together and move off with the same velocity. In a perfectly elastic collision, kinetic energy is conserved, and the two objects move off separately.
Simple Harmonic Motion
Question
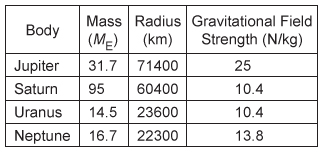
The mass, radius, and gravitational field strengths for four planets in our solar system are listed in the table above. Each planet's mass is given as a multiple of the mass of Earth M E. Which of the following correctly ranks the period P of identical pendulums near the surfaces of each planet?
| A. | |
| B. | |
| C. | |
| D. |
Explanation
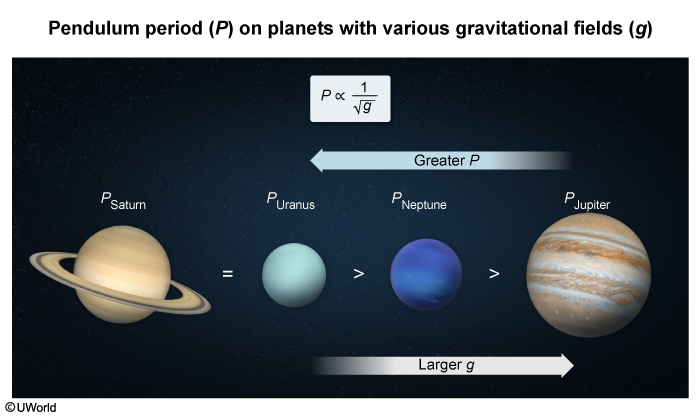
The period (P) of an object in simple harmonic motion is defined as the time it takes for the object to complete one cycle. For an ideal pendulum, the P of the pendulum bob is directly proportional to the square root of the pendulum length (L) but inversely proportional to the square root of the strength of the gravitational field (g):
The gravitational field strength g produced by an object of mass (M) is defined as the acceleration due to gravity experienced by a second, smaller object of mass m:
where (F g) is the gravitational force. Therefore:
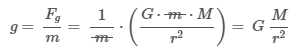
where G is the gravitational constant and r is the distance between the centers of the two objects.
In this question, P for a pendulum is considered on four planets in our solar system. The given table contains the values of M, the surface radius (r = R), and g for each planet. However, only the last column is relevant because P is proportional to (ie, the period is related to both and R). The pendulum will have the greatest value of P on the planet(s) with the smallest value of g . Therefore, it follows from the table that:
(Choice A) P is greatest when g is weakest, not just when the radius is greatest.
(Choice B) Here the values of P coincide with the mass ordered from largest to smallest. However, the value of P decreases as mass increases.
(Choice C) P decreases with an increase in g. In this answer, the planet with greatest P is listed as the planet with the greatest g rather than the smallest g.
Things to remember:
The gravitational field strength of a planetary object depends on both its mass and its radius. Larger values of gravitational field strength will produce smaller periods of a pendulum.
Question
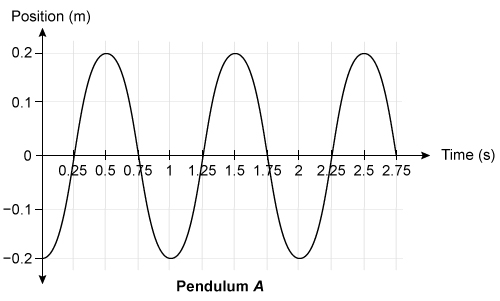
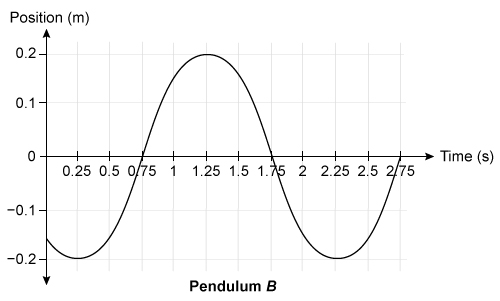
Two pendulum systems, A and B, are released and oscillate in a classroom lab. A motion detector is used to produce a graph of horizontal position as a function of time for each bob, as shown above. Which of the following statements about the oscillating systems are correct? Select two answers.
| A. Pendulum A is shorter than pendulum B. | |
| B. Pendulum B has a greater mass than pendulum A. | |
| C. Both pendulum systems oscillate with equal amplitude. | |
| D. Both pendulum systems move with equal speed at 1.5 s. |
Explanation
A pendulum is a system consisting of a mass m (ie, the bob) attached to the end of a light string or a rod with length L. When the bob is displaced a small angle θ (eg, θ ≤ 10°) from its equilibrium position (ie, hanging straight down), a component of the bob's weight acts as a restoring force and pushes the bob back to equilibrium. This force F is approximately the ratio of the linear displacement from equilibrium x and L:
The pendulum moves back and forth in simple harmonic motion like a mass-spring system because F has the form of an elastic force, with an effective spring constant k equal to:
Hence, the period of a pendulum T equals:
where g is the free-fall acceleration at a given location. Consequently, the bob's mass and the amplitude (ie, the maximum displacement of the bob from equilibrium) have no effect on the period.
In this question, two pendulum systems oscillate in the same location. Thus, both systems experience the same gravitational field strength. The period for each pendulum is represented on its graph of position as a function of time as the separation time between two consecutive maxima (or two consecutive minima):
Hence, the period for A is half that of B:
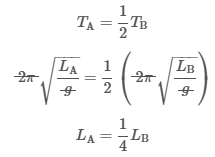
The amplitude A of each pendulum can be determined from the maximum positive (or negative) position on the graph:
Therefore, pendulum A is shorter than pendulum B, and both systems oscillate with the same amplitude.
(Choice B) The mass of a pendulum does not affect its period of oscillation for small angles (θ ≤ 10°) of oscillation.
(Choice D) The speed of each pendulum at 1.5 s is equal to the instantaneous slope of each graph at that time and is greater for pendulum B than for pendulum A.
Things to remember:
The period of a pendulum depends on its length and free-fall acceleration but not its mass or amplitude.
Question

Three blocks are suspended vertically from three springs and set into oscillation. The mass m, spring constant k, and the amplitude A of each setup are indicated above. Which of the following correctly relates the period of oscillation T of each block?
| A. | |
| B. | |
| C. | |
| D. |
Explanation

An object attached to a spring is subject to an elastic force governed by Hooke's law and therefore oscillates in simple harmonic motion. The period T of a mass-spring system depends on the square root of the ratio of the oscillating object's mass m to spring constant k:
Hence, the amplitude of the object′s motion does not affect the period of an oscillating mass-spring system.
In this question, the period of each mass-spring system can be determined using the provided mass and spring constant for each setup:
Therefore, the period for spring 1 and spring 2 are equal, and both are less than the period for spring 3:
(Choice A) A period ranking of T1 < T2 < T3 follows the rankings of the masses m1 < m2 < m3, but period also depends on the spring constant.
(Choice B) A period ranking of (T2 = T3) < T1 follows the rankings of the spring constants (k2 = k3) < k1, but period also depends on mass.
(Choice C) A period ranking of (T1 = T3) < T2 follows the rankings of the amplitudes (A1 = A3) < A2, but period does not depend on amplitude.
Things to remember:
The period of a mass-spring system depends on both mass and the spring constant, but not amplitude.
Torque and Rotational Motion
Question
A student dives into a pool from a height of 10 m. The diver is in a tuck and is rotating with angular momentum L as she descends into the pool. Halfway to the water, she extends her arms and legs so her body is elongated. If air resistance is negligible, which of the following accurately describes the change in angular speed of the diver after she elongates her body?
| A. The angular speed is unchanged because there is no net external torque on the diver. | |
| B. The angular speed is unchanged because the mechanical energy of the diver does not change. | |
| C. The angular speed decreases because her rotational inertia increases. | |
| D. The angular speed increases because her angular momentum increases. |
Explanation

Angular momentum (L) is defined as an object's rotational inertia (I) multiplied by its angular speed (ω):
Furthermore, the rotational inertia of any object rotating about an axis through its center is directly proportional to the product of the object's mass (m) and the square of the radial distance (r) from the axis of rotation:
Moreover, when no external torque is applied on the object, the change in the object's angular momentum is zero, and the angular momentum of the system is conserved:
In this question, the L of the diver is conserved because the gravitational force applies zero torque as she falls. When the diver elongates her body, she redistributes mass farther from the axis of rotation, increasing r and thus increasing her I. Because L is constant, her ω must also decrease. Therefore, increasing rotational inertia results in a decreasing angular speed when angular momentum is conserved.
(Choices A and D) Because angular momentum is conserved (remains unchanged), increasing rotational inertia results in a decreased angular speed.
(Choice B) Mechanical energy of the diver is conserved. However, angular speed decreases when rotational inertia increases because angular momentum is conserved.
Things to remember:
Angular momentum conservation implies that increasing rotational
inertia results in a decreased angular speed.
Question
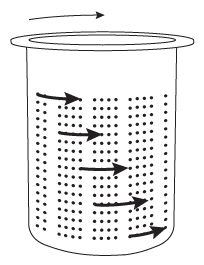
A system composed of a washing machine drum and the water in the drum spins freely as water escapes from holes in the side of the drum, as shown above. Which of the following must be correct about the resulting change in angular momentum of the system once the water has escaped?
| A. The angular momentum of the system changes by an amount equal to the momentum of the escaping water. | |
| B. The angular momentum of the system is constant. | |
| C. The angular momentum of the system increases. | |
| D. The angular momentum of the system decreases. |
Explanation
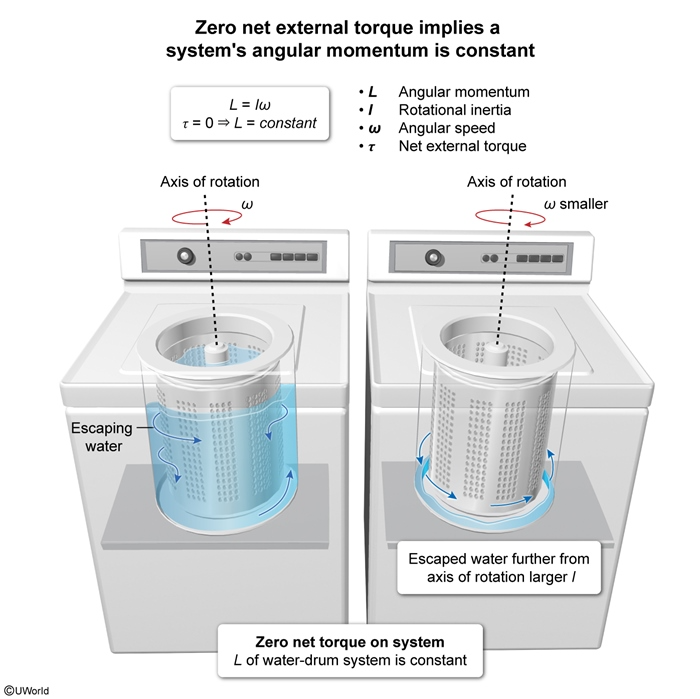
The angular momentum L of a rotating system equals the product of the system's rotational inertia I and angular speed ω:
Rotational inertia is a quantity that indicates how the mass of a system is distributed relative to the axis of rotation. The object's rotational inertia is larger (smaller) if more of a system's mass is located further away from (closer to) its axis of rotation.
When applied to a rotating system, Newton's second law of motion implies that the change in the angular momentum ΔL over time interval Δt equals the net external torque τ applied to the system:
However, when the net torque is zero, there is conservation of angular momentum and L is constant:
In this question, the system composed of the drum and the water experiences zero net external torque because the drum spins freely. Hence:
Therefore, the angular momentum of the system is constant.
(Choice A) The momentum of the escaping water does not equal the change the system's L. Only a net external torque can change L.
(Choice C) The I of the drum-water system increases as the water escapes and travels further away from the axis of rotation. However, conservation of angular momentum implies ω decreases and L remains constant.
(Choice D) The ω of the system decreases as I increases, but L remains constant because no external net torque is applied.
Things to remember:
Angular momentum of a system is conserved when there is zero net
torque exerted on the system. Therefore, a change in rotational inertia results in a change in a
system's angular speed, not angular momentum.
Question
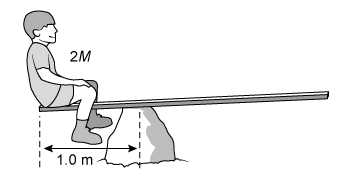
The figure above shows a child with mass 2M sitting at the end of a plank with a length of 4.0 m and a uniform mass M. The child is sitting a distance of 1.0 m to the left of the fulcrum, as shown above. How far from the child of mass 2M must a second child with mass M sit to keep the plank in equilibrium?
| A. 1.0 m | |
| B. 2.0 m | |
| C. 3.0 m | |
| D. 4.0 m |
Explanation
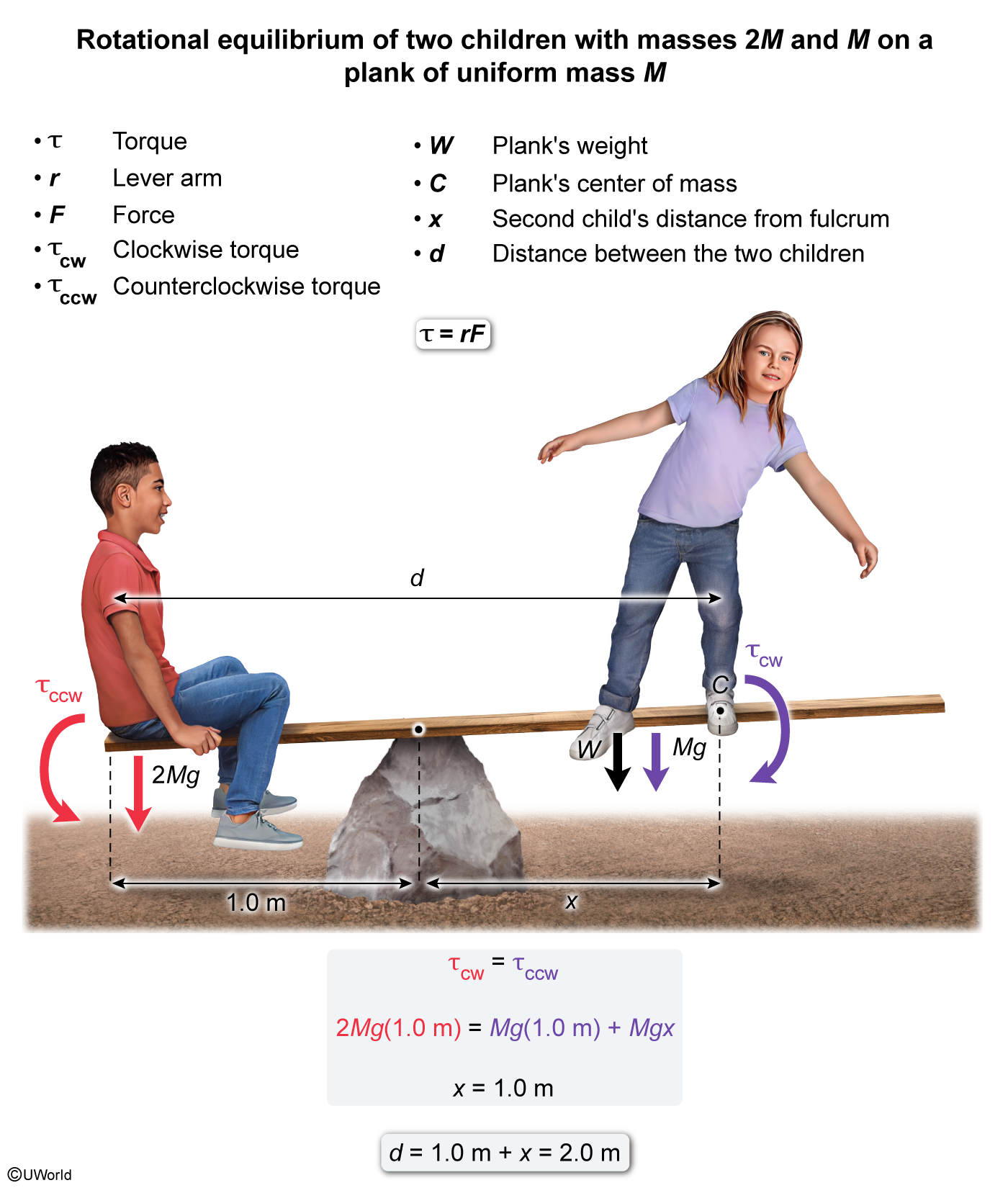
Torque is generated when a force F acts a perpendicular lever arm distance r⊥ away from an axis of rotation:
Rotational equilibrium is achieved when the sum of torques in the clockwise direction and in the counterclockwise direction (assigned a negative sign by convention) is zero:
Therefore:
In this question, the child with mass 2M sits 1.0 m from the fulcrum. The weight W of the child is a perpendicular force applied to the plank resulting in a torque in the counterclockwise direction:
On the other hand, two forces produce a clockwise torque on the plank: the weight of the plank located at its center of mass (COM) and the weight due to the second child of mass M. The COM of the plank is at a distance of 1.0 m to the right of the fulcrum, and the child sits at an unknown distance x to the right of the fulcrum. Consequently, the total torque produced in the clockwise direction is:
Applying the rotational equilibrium condition, the clockwise torque is equal to the counterclockwise torque:
Solving for x yields:
This means the second child must sit 1.0 m to the right of the fulcrum. Therefore, the second child is 2.0 m away from the first child:
(Choice A) If the second child sits 1.0 m from the first child, then the second child is sitting at the fulcrum and therefore generates zero balancing torque.
(Choices C and D) If the second child is 3.0 m or 4.0 m away from the first, then the clockwise torque will exceed the counterclockwise torque and disturb rotational equilibrium.
Things to remember:
Torque is the product of force and the perpendicular lever arm distance. Rotational equilibrium is achieved when the net torque on an object is equal to zero.
Make the AP Physics 1 Exam Feel Like Practice
Our AP Physics 1 practice tests and quizzes are just like the exam and make you think critically. They’ll teach you to spot trick answers, handle time pressure and boost your confidence for test day! Practice with realistic exam simulations so test day feels like just another practice run.
One Click AP Physics 1 Quizzes
Practice Under Real Exam Conditions
Study with Exam-Aligned Questions
Achieve Higher AP Physics 1 Exam Scores with Smart Study Tools
Exceptional Explanations for Every AP Physics 1 Question
Understand the “why” behind each concept with clear, step-by-step breakdowns. Our vivid explanations simplify complex ideas so you’ll ace the AP Physics 1 test. With visuals and cognitive learning principles, you’ll retain knowledge longer and avoid common pitfalls.
Flashcards & Notes That Help You Actually Remember
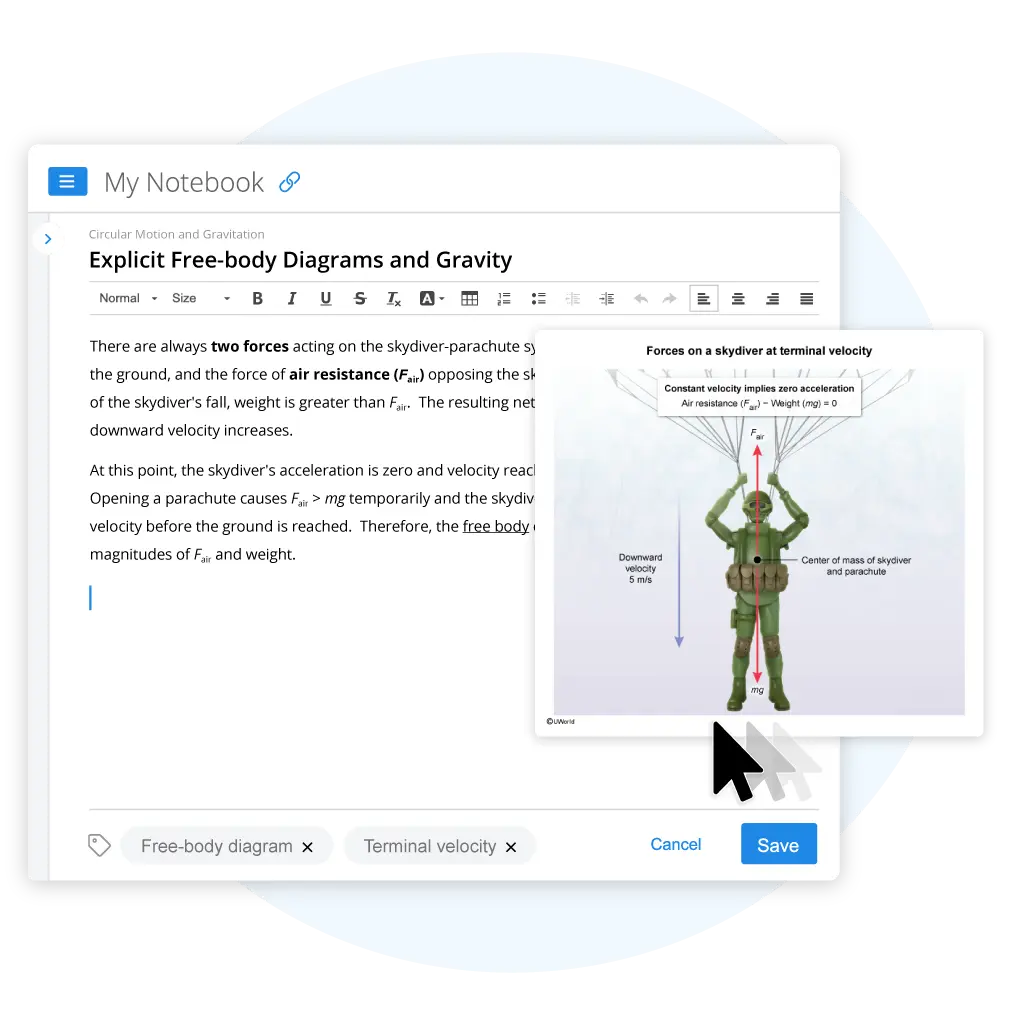
Create digital flashcards to practice the concepts you struggle with most, like how conservation of momentum applies in collisions or the difference between static and kinetic friction, helping you remember information months later, not just for the next unit quiz. Use My Notebook to organize key concepts from AP Physics 1 practice questions in the format that works best for you, whether that’s bullet points for steps to solve a kinematics problem, free-body diagrams for different scenarios, or detailed notes on how energy conservation applies to simple harmonic motion. One-click transfer from explanations to your flashcards or notebook means everything you need stays in one organized place.
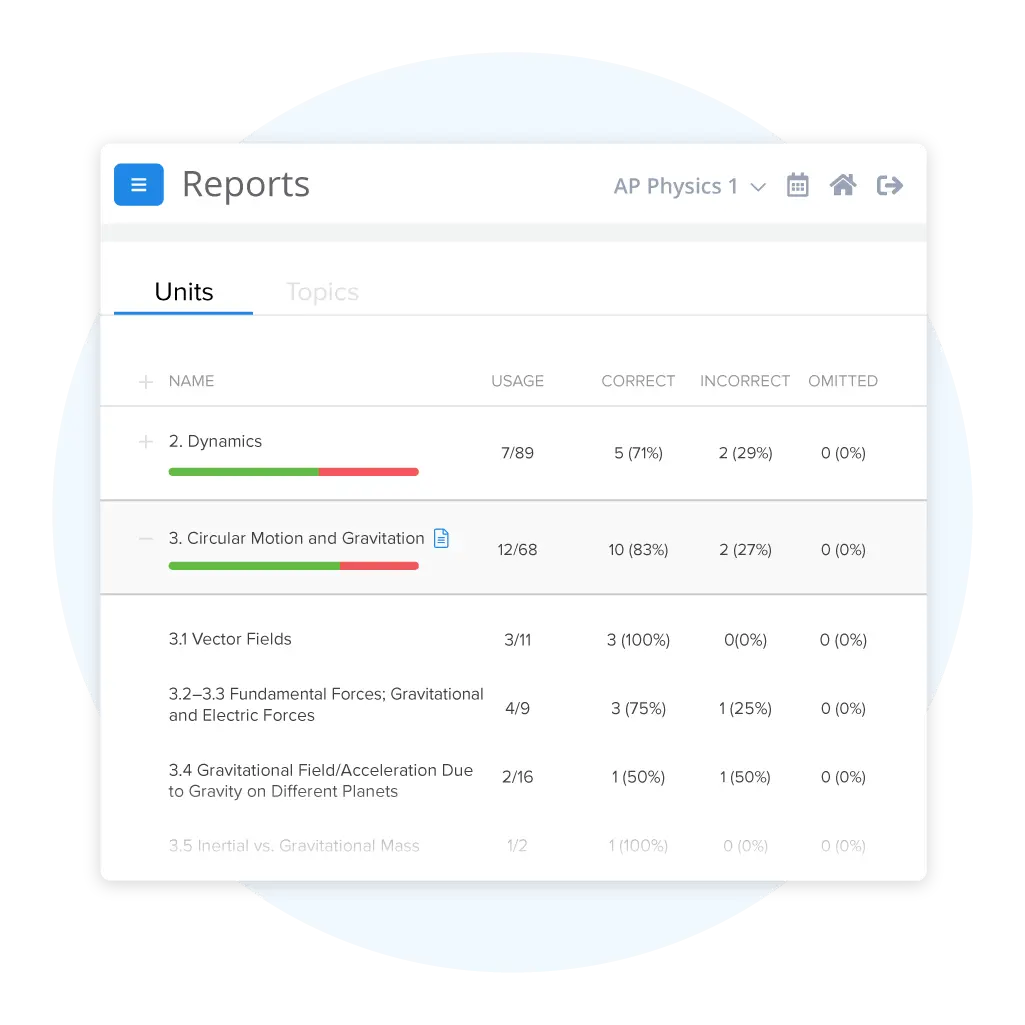
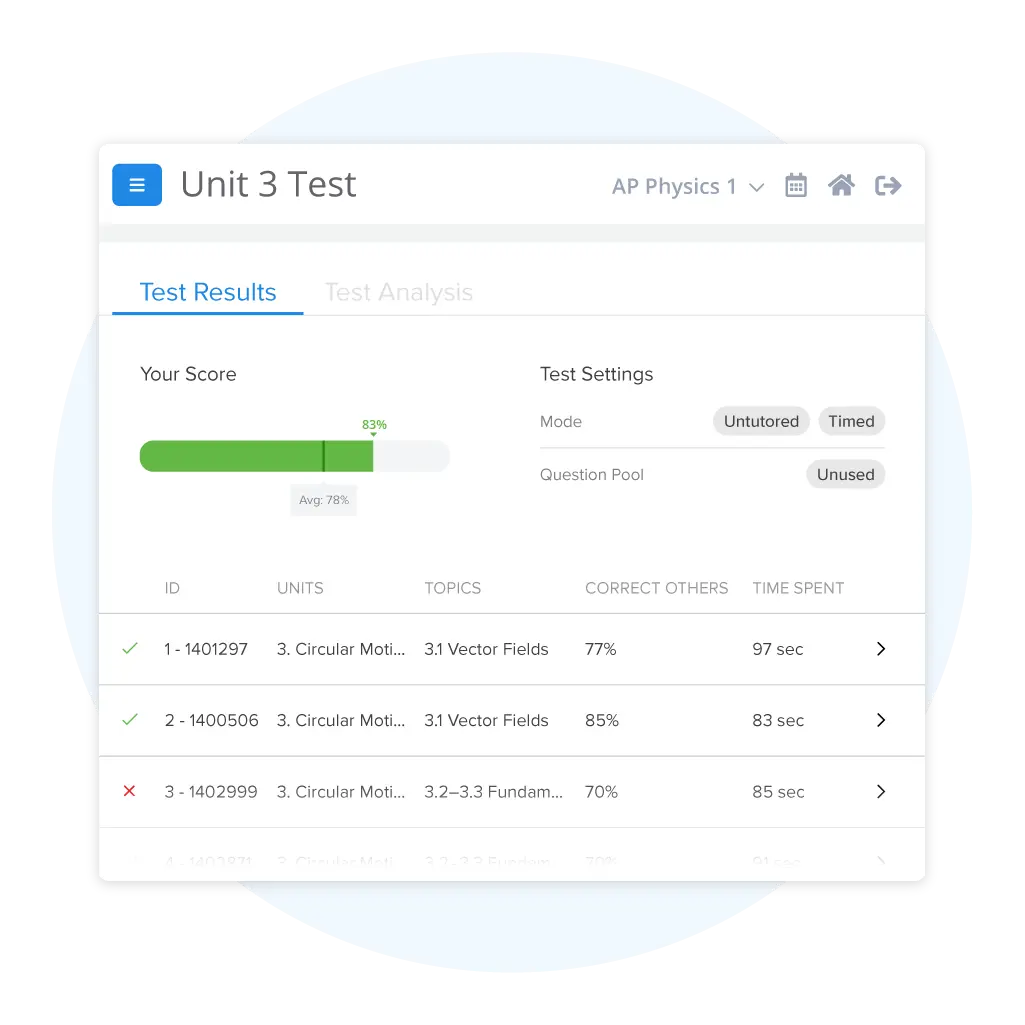
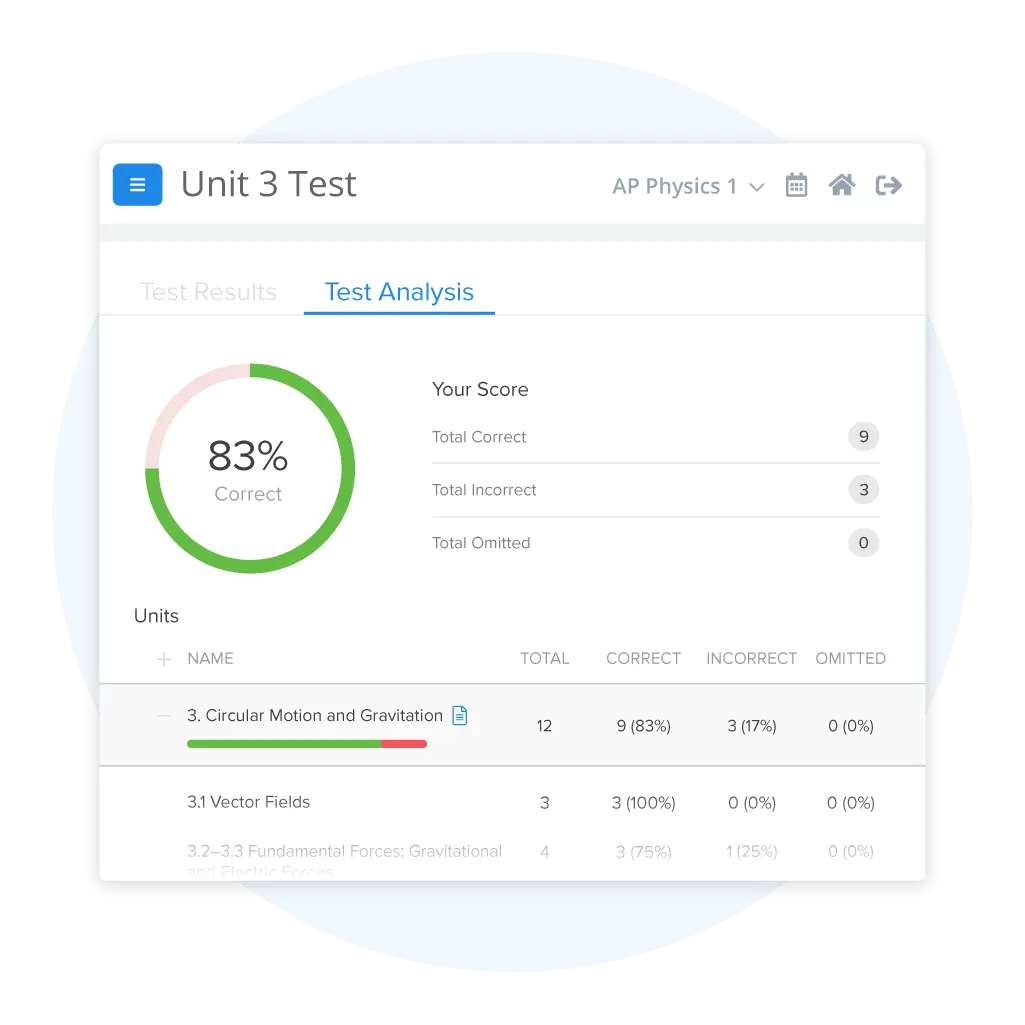
Track Your Progress and Target Weak Spots
See exactly where you stand with detailed performance tracking across all your AP Physics 1 practice tests and practice questions. Our analytics dashboard shows which topics you're crushing and which ones need more work. Focus your study time on actual weak areas, stop wasting time on stuff you already know, and watch your scores improve.
Pick Your AP Physics 1 Prep Package
Everything you need to pass the AP Physics 1 exam
450+ AP Physics 1 Practice Questions (MCQs)
Custom AP Physics 1 Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
450+ AP Physics 1 Practice Questions (MCQs)
Custom AP Physics 1 Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
Realistic FRQ Practice with Scoring Guide*
Score-Predicting Full-Length AP Physics 1 Mock Exam*
Print and Digital Study Guide
90+ Check-for-Understanding Questions
Expert-led Video Lessons
* Coming Winter 2025/Spring 2026
AP Physics 1 Practice Test Reviews
UWorlds multiple choice questions are similar to the ones on the official AP exam and allowed me to time myself for each question. This was very helpful for me as I was able to answer questions faster and could finish the questions on the actual exam. The explanations for each question went in-depth and gave important details pertaining to events in the timeline. Through this, I was able to gain important skills for the exam and get a 5.
Before, I had a hard time studying and staying focused because it was just boring, but now with UWorld, not only can I focus, but I actually feel motivated to learn!
The explanations were clear and I could practice the question based on units. I got a 5 in the end!! So, I think it’s very helpful and I’ll be using it to study for my future exams 🙂 You guys provide so many different functions to help students like me, and I really appreciate it, it’s really worth the money.
AP Physics 1 Practice Tests: Frequently Asked Questions (FAQs)
How closely do UWorld's AP Physics 1 practice tests match the real exam?
Why choose UWorld’s AP Physics 1 practice exam over free online options?
Does the UWorld AP Physics 1 question bank cover all required topics?
Yes. Our AP Physics 1 practice test generator and question bank provides comprehensive coverage of all 8 units from the College Board curriculum:
- Kinematics
- Force and Translational Dynamics
- Work, Energy and Power
- Linear Momentum
- Torque and Rotational Dynamics
- Energy and Momentum of Rotating Systems
- Oscillations
- Fluids
With more than 450 AP Physics 1 practice questions, you can build customized tests and quizzes across all topics or focus on specific units where you need targeted review.
What’s the best way to use AP Physics 1 practice tests as part of my study routine?
Start by using our bank of AP Physics 1 practice questions in short, topic-focused quizzes to identify your knowledge gaps. After each AP Physics 1 practice test or quiz, we encourage students to meticulously review the detailed explanations for every question, including those you answered correctly. This helps you master the underlying physics concepts, not just memorize answers.
Throughout your prep, use the performance dashboard to track which AP Physics units and concepts need more attention, then create targeted AP Physics 1 practice exams to drill on them. This focused strategy is the most efficient path to building the deep conceptual understanding required for a 5 on the exam.