AP® Physics 1 Equation and Formula Sheet

While the AP® Physics 1 equation sheet is hugely beneficial to students as a quick-check resource, it is still crucial to understand the material provided and be able to explain what the equations and/or expressions represent. In addition, it is expected that students have seen and used each of the listed equations in their AP Physics 1 classes and that the variables provided in the list of unit symbols are largely conventional and quickly recognized.

In any case, a student must be able to apply the equations and information provided in the AP Physics 1 formula sheet to scenarios presented in the multiple-choice and free-response sections of the AP Physics 1 exam. Below, you will find everything you need to know about the information provided on the AP Physics 1 equation sheet:

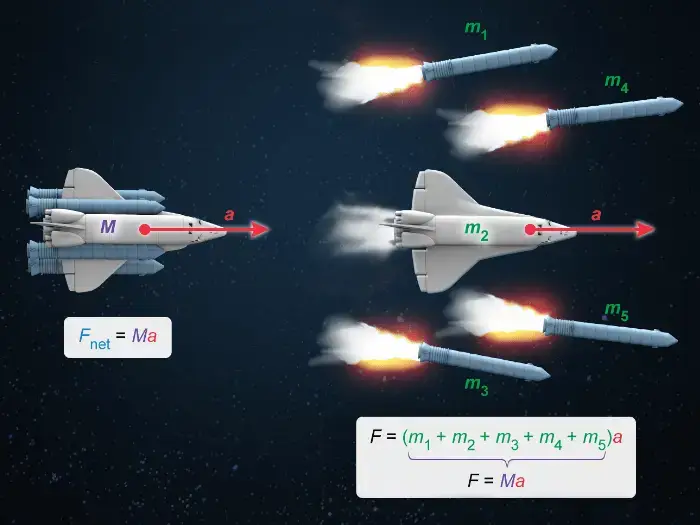
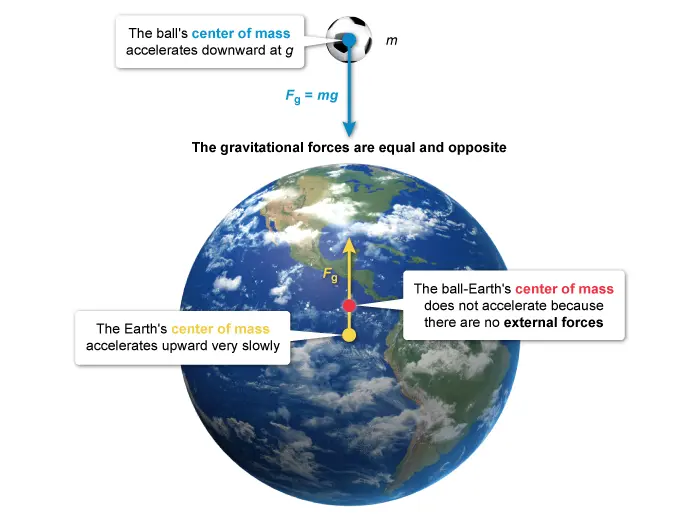
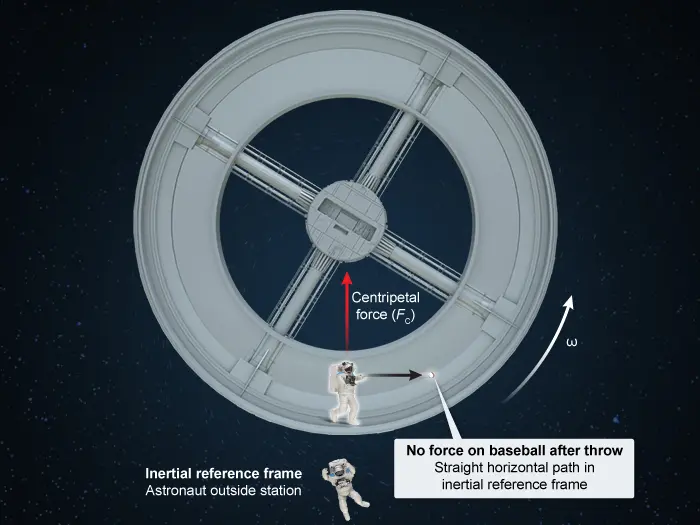
What is the AP Physics 1 Equation Sheet & Formula Sheet?

The AP Physics 1 equation sheet provides students with critical information necessary for success on the AP Physics 1 exam. The sheet includes the major equations used in each unit, the trigonometric functions used in the course, and other related constants, conversion factors, unit symbols, and prefixes. At first glance, a student might be overwhelmed by the AP Physics 1 formula sheet. However, the main purpose of the sheet is to provide an organized array of AP Physics 1 equations so that a student does not need to memorize everything.

Constants and conversion factors

Students are provided with important constants that are often needed throughout the AP Physics 1 exam. These values are typically naturally occurring and do not change:

Proton mass, m_p= 1.67 x 10^-27 kg	Electron charge magnitude, e = 1.60 x 10^-19 C
Neutron mass, m_n= 1.67 x 10^-27 kg	Coulomb's law constant, k = 1/4_πε₀ = 9 x 10⁹ N.m²/ C²
Electron mass, m_e= 9.11 x 10^-31 kg	Universal gravitational constant , G = 6.67 x 10^-11 m³/ kg.s²
Speed of light, c = 3.00 x 10⁸ m/s	Acceleration due to gravity at Earth's surface, g = 9.8 m/s²

Unit symbols

Next on the AP Physics 1 formula sheet are the unit symbols. There are many symbols, including greek letters, that can be used to represent the physical units associated with a number. Most symbols are chosen by convention and are used in the same way throughout various textbooks. Therefore, as shown below, the AP Physics 1 equation sheet provides a list of all the symbols that might be used on the AP Physics 1 exam:

meter	m	joule	J
kilogram	kg	watt	W
second	s	coulomb	C
ampere	A	volt	V
kelvin	K	ohm	Ω
hertz	Hz	newton	N
degree Celsius	°C

Prefixes

The scientific prefixes are used throughout various disciplines to represent large and small numbers in a more readable way. Thus, the prefixes listed below are printed on the AP Physics 1 equation sheet for easy reference:

Factor	Prefix	Symbol
10¹²	tera	T
10⁹	giga	G
10⁶	mega	M
10³	kilo	k
10^-2	centi	c
10^-3	milli	m
10^-6	micro	µ
10^-9	nano	n
10^-12	pico	p

Values of trigonometric functions for common angles

A chart on the AP Physics 1 formula sheet includes the values for the sine, cosine, and tangent at several common angles. These are known as trigonometric values:

θ	0°	30°	37°	45°	53°	60°	90°
sinθ	0	1/2	3/5	√2/2	4/5	√3/2	1
cosθ	1	√3/2	4/5	√2/2	3/5	1/2	0
tanθ	0	√3/3	3/4	1	4/3	√3	∞

Equations commonly used in physics for mechanics

The AP Physics 1 equation sheet contains all of the formulas and relationships that are needed to solve problems related to one-dimensional kinematics, Newton's laws of motion, work and energy, impulse and momentum, rotational motion, and simple harmonic motion. The breakdown of these equations is explained below:

One-dimensional motion

v_x = v_x0+a_xt

This equation represents the definition of constant acceleration. The final velocity of an object is equal to its initial velocity plus the product of the object's acceleration and the time the object is accelerating for.

v : speed, x : position, a : acceleration, t: time

x = x₀+v_x0 t + ¹⁄₂a_xt²

This equation can be used to relate the position, initial velocity, acceleration, and time for an object moving in one dimension. This relationship shows that the position of an object under constant acceleration is quadratic with respect to time.

x : position, v : speed, a : acceleration, t: time

v ²_x = v ²_x0 + 2a_x (x -x₀ )

This equation shows that the final velocity of an object squared is equal to its initial velocity squared plus the product of its acceleration and displacement (multiplied by 2).

v : speed, x : position, a : acceleration

Newton's laws of motion

a→ = ^ΣF→⁄_m = ^F→_net⁄_m

This equation is Newton's second law of motion. The acceleration of an object is directly proportional to the net force acting on the object and inversely proportional to its mass.

a : acceleration, F : force, m : mass

|F_f→| ≤ μ|F_n→|

This equation describes the relationship between the force of friction and the normal force. The force of friction is always less than or equal to the product of the coefficient of friction and the normal force.

μ : coefficient or friction, F : force, f : frequency

a _c = ^{v ²}/_r

This equation indicates that the centripetal acceleration for an object moving in circular motion is equal to the ratio of the velocity squared and the radius of the circular path.

a : acceleration, v : speed, r : radius or separation

|F_s→| = k |x→|

This equation represents the spring force. The spring force is equal to the product of the spring constant and the displacement of the spring from its equilibrium position.

F : force, k : spring constant, x : position

ρ = ^m/_V

This equation is the equation for density. Density is equal to the ratio of the mass of an object to its volume.

ρ : density, m : mass , V : volume

|F_g→| = G^m₁m₂/_{r ²}

This equation is Newton's law of gravitation. The force of gravity between two objects is directly proportional to the product of the gravitational constant and each mass, while inversely proportional to the square of the distance between the masses.

F : force, m : mass , r : radius or separation

g→ = ^{F_g →}/_m

This equation shows that the gravitational field strength (ie, gravitational acceleration) that an object experiences is equal to the ratio of the gravitational force acting on the object and its mass.

F : force, m : mass

Work and energy

K = ¹/₂ mv ²

This equation represents the kinetic energy of an object, which is equal to the product of one-half the mass of the object and the square of its velocity.

K : kinetic energy, m : mass, v : speed

ΔE = W = F_|| d = Fd cosθ

This equation is the work-energy theorem. The change in energy of a system (ie, the work done) is equal to the product of the parallel component of the net force acting on an object and its displacement.

E : energy, W : work done on a system , F : force, d : distance

P = ^ΔE/_Δt

This equation can be used to determine the power output of a system, which represents the rate of change of energy with respect to time.

P : power, E : energy, t : time

U_s = ¹/₂ kx ²

This equation is the potential energy stored within a spring. This type of elastic potential energy is equal to the product of one-half the spring constant and the square of the displacement of the spring from its equilibrium position.

U : potential energy, k : spring constant, x : position

ΔU_g = mg Δy

This equation describes the change in the gravitational potential energy of a system, which is equal to the product of the mass of the object, the gravitational field strength, and the displacement of the object throughout the field.

U : potential energy, m : mass , y : height

U_G = -G ^m₁m₂/_r

This equation alternatively describes the gravitational potential energy between two objects, which is directly proportional to the negative product of the gravitational constant and each mass, while inversely proportional to the distance between the masses.

U : potential energy, m : mass , r : radius or separation

Impulse and momentum

p→ = mv→

This equation represents the definition of linear momentum. The momentum of an object can be determined from the product of its mass and velocity.

p : momentum, m : mass , v : speed

Δp→ = F→Δ t

This equation is the impulse-momentum theorem. The change in momentum of an object or system is equal to the product of the force acting on the system and the time over which the force acts.

p : momentum, F : force , t: time

Rotational motion

θ = θ₀ + ω₀t + ¹/₂ αt ²

This equation can be used to relate the angular position, initial angular velocity, angular acceleration, and time for an object moving in rotational motion. This relationship shows that the angular position of an object under constant angular acceleration is quadratic with respect to time.

θ : angle, ω : angular speed, t: time , α : angular acceleration

ω = ω₀ + αt

This equation represents the definition of constant angular acceleration. The final angular velocity of an object is equal to its initial angular velocity plus the product of the object's angular acceleration and the time for which it accelerates.

ω : angular speed, t: time , α : angular acceleration

α→ = ^Στ→⁄_I = ^τ→_net⁄_I

This equation is Newton's second law of motion in the rotational sense. The angular acceleration of an object is directly proportional to the net torque acting on the object and inversely proportional to its rotational inertia.

α : angular acceleration, τ : torque , I : rotational inertia

τ = r_⊥F = rF sinθ

This equation shows the relationship between a linear force and a torque. To determine the torque generated by a force, compute the product of the force, the distance the force is applied from a rotational axis (ie, the lever arm), and the angle between the force and the lever arm.

τ : torque, F : force, θ : angle, r : radius or separation

L = I ω

This equation indicates the definition of angular momentum. The angular momentum of an object can be determined from the product of its rotational inertia and its angular velocity.

L : angular momentum, I : rotational inertia, ω : angular speed

ΔL = τ Δt

This equation is the impulse-momentum theorem in the rotational sense. The change in angular momentum of an object or system is equal to the product of the torque acting on the system and the time over which the torque acts.

L : angular momentum, τ : torque , t: time

K = ¹/₂ I ω²

This equation displays the rotational kinetic energy of an object, which is equal to the product of one-half the rotational inertia of the object and the square of its angular velocity.

K : kinetic energy , ω : angular speed, I : rotational inertia

Simple harmonic motion

x = Acos ( 2Πft )

This equation shows that the position of a point within an oscillating medium is equal to the product of the amplitude and the cosine of the frequency and time.

x : position, A : amplitude, f : frequency, t: time

T = ^2Π/_ω = ¹/_f

This equation is the simple relationship between frequency, angular frequency, and period. The period is inversely proportional to the frequency. However, the period is directly proportional to 2*pi and inversely proportional to angular frequency.

T : period, ω : angular speed, f : frequency

T_s = 2 Π√^m/_k

This equation represents the period of an oscillating mass-spring system. The period is equal to the product of 2*pi and the square root of the ratio between the mass and the spring constant.

T : period, m : mass, k : spring constant

T_p = 2 Π√^ℓ/_g

This equation gives the relationship for the period of a swinging pendulum. The period of the pendulum is equal to the product of 2*pi and the square root of the ratio between the length of the pendulum and the gravitational field strength.

T : period, ℓ : length

Equations commonly used in physics for geometry and trigonometry

The AP Physics 1 equation sheet also contains all of the mathematical formulas and relationships that could be needed to deal with geometry and trigonometry. These equations can be used to determine areas, volumes, and right-triangle side and angle relationships.

Rectangle

A = bh

Triangle

A = ¹/₂ bh

Circle

A = πr²

C = 2πr

Rectangular Solid

V = ℓwh

Cylinder

V = πr²ℓ

S = 2πrℓ + 2πr²

Sphere

V = ⁴/₃πr³

S = 4πr²

A = area

C = Circumference

V = Volume

S = surface area

b = base

h = height

ℓ = length

w = width

r = radius

Right triangle

c² = a² + b²

sin θ = ^a/_c

cos θ = ^b/_c

tan θ = ^a/_b

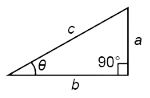
Geometry

The equations necessary to calculate the area, circumference, volume, and surface area are provided for a rectangle, triangle, circle, rectangular solid, cylinder, and sphere. The area of a rectangle and a triangle are most useful from this section as they are needed to determine the area under the curve for various graph-related questions.

Trigonometry

The right triangle relationships listed on the equation sheet are extremely important when dealing with vector relationships on the AP Physics 1 exam. The sine, cosine, and tangent of an angle within a right triangle are related to specific ratios involving the length of the sides of the right triangle. Moreover, the Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides of the triangle.

Using the AP Physics 1 Formula Sheet

As you work through multiple-choice and free-response questions for the AP Physics 1 exam, be sure to reference the AP Physics 1 equation sheet often! Prior to taking the exam, you should become familiar with the layout of the AP Physics 1 formula sheet (ie, where in the formula sheet certain equations/constants are located) so that you can quickly find them when solving a problem.

With this knowledge, you'll be able to quickly find equations and information as needed on exam day!

The equations for “Electricity” and “Waves” are no longer covered on the AP Physics 1 exam.