We will start by breaking down the format of Section II of the AP Calculus BC exam and giving tips to maximize your points on the FRQs. In the following sections, we have also included a few examples of AP Calculus BC free-response questions you might see on the exam. By the end of this article, you will know how to practice AP Calculus BC FRQs as you prepare for your upcoming AP Calculus BC exam.
Format of the AP Calculus BC Free-Response Section
Let’s start this section by answering the most frequently asked question: “How many FRQs are on the Calculus BC exam?” The FRQ section of the AP Calculus BC exam is split into two parts: Part A and Part B. Part A consists of two questions on which you are allowed to use a calculator, and you are given 30 minutes to complete them. Part B consists of four questions for which a calculator is not allowed, and you get one hour to address this part.
The entire Section II accounts for 50% of the total points on the exam, where each question is weighted the same regardless of whether it is in Part A or B. The questions cover all 10 units of the AP Calculus BC course. The table below summarizes the crucial information about the format of the MCQ section on the AP Calculus BC exam:
| Section II | Part A | Part B |
| No. of Questions | 2 FRQs | 4 FRQs |
| Exam Weight | 16.7% | 33.3% |
| Time Allotted | 30 minutes | 1 hour |
| Calculator Usage | Permitted | Not Permitted |
How to Answer AP Calculus BC’s Free-Response Questions
Here are some tips for approaching the FRQ section of the AP Calculus BC exam:
-
Read all the questions thoroughly.
Begin by reading through all the questions in the section. Identify the topics you’re most confident in and start with those. This strategy helps you secure easy points early, boosts your confidence, and allows you to focus on the more challenging questions later.
-
Annotate important information.
As you read each question, add notes or highlight key details such as vocabulary, given values, function definitions, and the specific quantity asked. This will help you stay focused on what matters most. Pay attention to vocabulary like "relative maximum" and recall its meaning in calculus, such as when the derivative equals zero and changes from positive to negative or when the second derivative is negative.
-
Treat each part of every FRQ independently.
Some parts of the FRQ questions may be related. For instance, Part A might ask you to estimate a Riemann sum, and Part B might ask you to determine if your result in Part A is overestimated or underestimated. Even if you are unsure about your Part A answer, proceed with Part B as if your Part A answer were correct. Readers grade each part independently, so you can still earn full points for Part B by providing the correct interpretation, regardless of any errors in Part A.
-
Organize your work.
As you prepare for the exam, use the College Board® scoring guidelines to study what kinds of things they instruct the readers to look for. When you answer questions on the exam, only include the information you need to score points. If you need to write things down as you work toward your answers, do so in the question booklet.
-
Save time, draw a line.
If you make an error and catch it, do not erase it. Instead, draw a line or X through the sections you don’t want the readers to consider. Doing this saves time over erasing.
-
Show your work.
Unless the question explicitly tells you to simplify or give a numerical answer, leave your answers in their original, complete form. The scorers will accept your response in any format as long as you've completed the work required by the question. While preparing for the exam, understand the scoring guidelines and study the sample answers from the College Board. This will give you an even better idea of when you should or should not simplify your answers.
-
Use your calculator wisely for Part A.
The following are four functionalities that the College Board expects your graphing calculator to do:
- Plot the graph of a function within an arbitrary viewing window.
- Find the zeros of functions (solve equations numerically).
- Numerically calculate the derivative of a function.
- Numerically calculate the value of a definite integral.
You are not expected to show intermediate steps when you need to do any of these four things in a Part A FRQ. Just show the setup correctly, plug it into your calculator, and give the numerical answer.
-
Return to Part A.
If you haven't completed your responses in Part A and find extra time after tackling the Part B questions, revisit the Part A questions to complete any unfinished work. However, remember that you won't have access to your calculator during this time, which may restrict what you can accomplish.
Correct any mistakes in setting up an integral or equation, even if you can't compute the result without a calculator. Setting up the problem correctly can still earn you points, even without arriving at the correct numerical answer.
AP Calculus BC free-response question examples
Here are some examples of AP Calc BC FRQs from past exams to illustrate the different questions you will see on the exam. These questions come directly from the College Board and are an excellent source to practice with.
One of the question types that appear most frequently on the AP Calculus BC exam is a table of data modeling some real-world scenarios. The College Board will use the table to test concepts that allow you to calculate approximate values, like average rate of change and Riemann sums. The intermediate value theorem is another concept that is easily tested with tabular data. An example of this type of question (#4 from 2022) is shown below, with highlights demonstrating these common elements.
| t (days) |
0 | 3 | 7 | 10 | 12 |
| r ‘ (t ) (centimeters per day) |
−6.1 | −5.0 | −4.4 | −3.8 | −3.5 |
An ice sculpture melts in such a way that it can be modeled as a cone that maintains a conical shape as it decreases in size. The radius of the base of the cone is given by a twice-differentiable function r , where r (t ) is measured in centimeters and t is measured in days. The table above gives selected values of r’ (t ), the rate of change of the radius, over the time interval 0 ≤ t ≤ 12.
- Approximate r” (8.5) using the average rate of change of r’ over the interval 7 ≤ t ≤ 10. Show the computations that lead to your answer, and indicate units of measure.
- Is there a time t, 0 ≤ t ≤ 3, for which r’ ( t ) = −6 ? Justify your answer.
- Use a right Riemann sum with the four subintervals indicated in the table to approximate the value of ∫120r’ (t ) dt.
- The height of the cone decreases at a rate of 2 centimeters per day. At time t = 3 days, the radius is
100 centimeters and the height is 50 centimeters. Find the rate of change of the volume of the cone with respect
to time, in cubic centimeters per day, at time t = 3 days. (The volume V of a cone with radius r and height h is V = 1⁄3 πr 2h. )
Ref: College Board: Example 1 is on page 8 of
https://secure-media.collegeboard.org/apc/ap22-frq-calculus-bc.pdf
Another commonly asked free-response question in the AP Calculus BC exam is understanding meaning within a context. You will be asked to calculate a quantity and give an interpretation of what that quantity means within the given scenario. You will have to present your inference with the correct units, requiring you to understand how a derivative or integral changes the units of a function. This often occurs within a table question, but not always. The question below (2018 #2) is one such question.
Researchers on a boat are investigating plankton cells in a sea. At a depth of h meters, the density of plankton cells, in millions of cells per cubic meter, is modeled by p(h) = 0.2h2e-0.0025h2 for 0 ≤ h ≤ 30 and is modeled by f(h) for h ≥ 30. The continuous function f is not explicitly given.
- Find p’ (25). Using correct units, interpret the meaning of p’ (25) in the context of the problem.
- Consider a vertical column of water in this sea with horizontal cross sections of constant area 3 square meters. To the nearest million, how many plankton cells are in this column of water between h = 0 and h = 30 meters?
- There is a function u such that 0 ≤ f(h) ≤ u(h) for all h ≥ 30 and ∫∞30u (h ) dh. = 105. The column of water in part (b) is K meters deep, where K > 30. Write an expression involving one or more integrals that gives the number of plankton cells, in millions, in the entire column. Explain why the number of plankton cells in the column is less than or equal to 2000 million.
- The boat is moving on the surface of the sea. At time t ≥ 0, the position of the boat is (x(t), y(t)), where x'(t) = 662 sin(5t ) and y'(t) = 880 cos(6t). Time t is measured in hours, and x(t) and y(t) are measured in meters. Find the total distance traveled by the boat over the time interval 0 ≤ t ≤ 1.
Ref: College Board: Example 2 is on page 3 of
https://apcentral.collegeboard.org/pdf/ap18-frq-calculus-bc.pdf
Another thing to note about the FRQ section of the AP Calculus BC exam is that the College Board aims to test your ability to interpret data from a number of different presentations: functions, graphs, and tables. The question below (2022 #5) shows a graph of a function and asks about several concepts that tend to give students a lot of trouble: area and volume from Unit 8 and improper integrals from Unit 6.
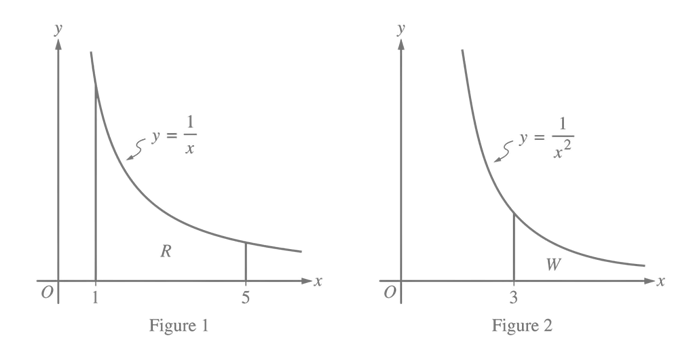
5. Figures 1 and 2, shown above, illustrate regions in the first quadrant associated with the graphs of y = 1 x and y = 1 x2 , respectively. In Figure 1, let R be the region bounded by the graph of y = 1 x , the x-axis, and the vertical lines x = 1 and x = 5. In Figure 2, let W be the unbounded region between the graph of y = 1 x2 , and the x-axis that lies to the right of the vertical line x = 3.
- Find the area of region R
- Region R is the base of a solid. For the solid, at each x the cross section perpendicular to the x-axis is a rectangle with area given by xe x/5. Find the volume of the solid.
- Find the volume of the solid generated when the unbounded region W is revolved about the x-axis.
Reference College Board: Example 3 is on page 9 of
https://secure-media.collegeboard.org/apc/ap22-frq-calculus-bc.pdf
On the AP Calculus BC exam, the sixth and final FRQ is always a power series from Unit 10. Most often, it includes a Taylor or Maclaurin polynomial or series, but it can take various forms. The example below is from 2021, and it includes a number of different techniques and concepts from throughout Unit 10. Study power series thoroughly and be prepared for this concept to feature prominently in an FRQ.
The function g has derivatives of all orders for all real numbers. The Maclaurin series for g is given by g(x) = ∞ Σ n = 0 (-1)n xn 2en + 3 on its interval of convergence.
State the conditions necessary to use the Integral test to determine convergence of the series ∞ Σ n = 0 1 en . Use the integral test to show that ∞ Σ n = 0 1 en converges.
Use the limit comparison test with the series ∞ Σ n = 0 1 en to show that thee series g (1) = ∞ Σ n = 0 (-1)n 2en + 3 converges absolutely.
- Determine the radius of convergence of the Maclaurin series for g.
The first two terms of the series g (1) = ∞ Σ n = 0 (-1)n 2en + 3 are used to approximate g (1). Use the alternating series error bound to determine an upper bound on the error of approximation.
Ref: College Board: Example 4 is on page 10 of
https://apcentral.collegeboard.org/pdf/ap21-frq-calculus-bc.pdf
How can I practice AP Calculus BC free-response questions?
The best way to practice for the AP Calculus BC exam is to use the College Board's previous years' exams. Our AP Calculus BC Online Prep Course offers comprehensive lessons on key topics, which you can watch or read to help maximize your score.
- Practice what you know:
Start by focusing on areas that align with your current knowledge. Begin with manageable sections of past FRQs to build your skills as you progress through the curriculum.
- Comprehensive FRQ Practice (Untimed):
Once you've mastered the content, practice full FRQ sections. Focus on recent exams, as question formats may change over time. Use the scoring guidelines and College Board rubrics to assess your work and understand how answers are graded.
For additional resources on approaching FRQ concepts, optimize your study time with our AP Calculus BC Study Guide, available in print and digital formats. This guide targets the material you need to master, helping you focus on areas that need improvement most.
- Comprehensive FRQ Practice (Timed):
Simulate real exam conditions by timing yourself while completing full FRQ sections. This will help you develop time management skills and prepare for the pressure of the actual exam.
- Full-length MCQ + FRQ Practice (Timed):
Once you feel confident with FRQs, tackle timed practice for both sections to replicate the full AP Calculus BC exam experience. Explore our AP Calculus BC Practice Questions for more MCQs to create a practice test.
Frequently Asked Questions
How are the AP Calculus BC free-response questions graded?
AP Calculus BC FRQs are graded by high school teachers and college professors using scoring guidelines provided by the College Board. A head reader resolves any grading ambiguities.
How long is the FRQ section of the AP Calculus BC exam?
The FRQ section of AP Calculus BC is an hour and a half long, split into two parts: 2 questions (30 minutes) and 4 questions (1 hour). You have an average of 15 minutes to answer each FRQ.
Where can I get the AP Calculus BC past exam FRQs?
You can find questions from past exams released on the AP Central website.
References
- AP Calculus AB and BC Course and Exam Description. (Fall, 2020). apcentral.collegeboard.org. Retrieved on December 13, 2024 from https://apcentral.collegeboard.org/media/pdf/ap-calculus-ab-and-bc-course-and-exam-description.pdf
- AP Calculus BC. (n.d.). apstudents.collegeboard.org. Retrieved on December 13, 2024 from https://apstudents.collegeboard.org/courses/ap-calculus-bc
- AP Calculus BC. (n.d.). apstudents.collegeboard.org. Retrieved on December 13, 2024 from https://apstudents.collegeboard.org/courses/ap-calculus-bc/assessment
- AP Calculus BC Free-Response Questions. (2018). apcentral.collegeboard.org. Retrieved on December 13, 2024 from https://apcentral.collegeboard.org/media/pdf/ap18-frq-calculus-bc.pdf
- AP Calculus BC Free-Response Questions. (2021). apcentral.collegeboard.org. Retrieved on December 13, 2024 from https://apcentral.collegeboard.org/media/pdf/ap21-frq-calculus-bc.pdf
- AP Calculus BC Free-Response Questions. (2022). secure-media.collegeboard.org. Retrieved on December 13, 2024, from https://secure-media.collegeboard.org/apc/ap22-frq-calculus-bc.pdf
Read More About AP Calculus BC Exam
Answering MCQs appears simple, but the correct answer can differ by a small margin. Here, we show you how to approach the right answer in AP Calculus BC Multiple Choice Questions.
AP Calculus BC Study Plan & TipsWhether you want to get a head start this summer or wait until two weeks before the exam preparation, we break down the essential tips and tricks regardless of your timeframe.
AP Calculus BC Exam FormatConfused about the AP Calculus BC Exam Format? Read this article for in-depth information on the AP Calculus BC Exam structure—question types, topic-wise weights, and more.
About AP Calculus BC ExamWondering if AP Calculus BC is right for you? Get thorough exam information on AP Calculus BC, including what’s on the exam, why to take it, exam prerequisites, and exam difficulty.
Best AP Calculus BC Study Guide ComparisonCompare the best AP Calculus BC study guides! See how Kaplan, Barron's, and Princeton Review stack up against UWorld for comprehensive exam prep.
Best AP Calculus BC Prep Course ReviewDiscover the best AP Calculus BC prep courses! This in-depth review helps you compare options and pick the course that meets your needs.
How to Self-Study for AP Calculus BCSelf-studying for AP Calculus BC? Use this proven step-by-step guide to master concepts, stay organized, and achieve top exam scores.