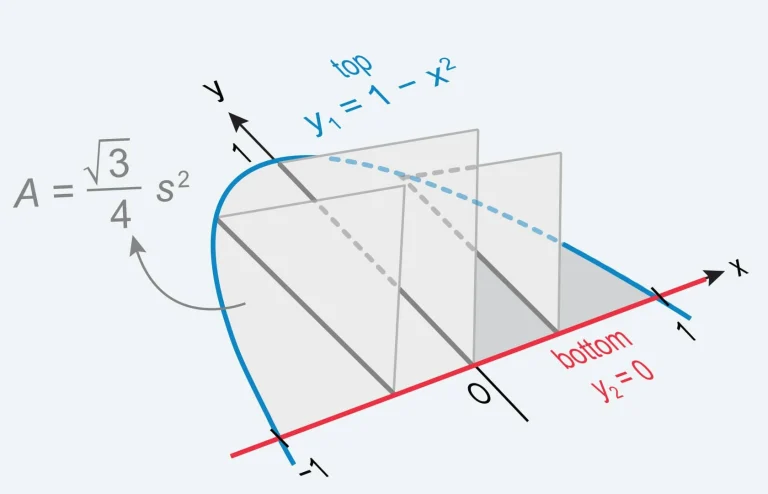
We’ve simplified the AP Calculus AB curriculum into easy-to-digest sections. This page offers a complete AP Calculus AB course outline, covering everything from prerequisites to key concepts and topics.
As you progress on your AP Calculus AB journey, our AP Calculus Study Guide can help you learn step by step as you go through the class or prepare for your AP exam. You can get it print or digital book format, and it’s made to explain every concept clearly and easily.
AP Calculus AB Units, Topics, and Key Concepts
The AP Calc AB course comprises two primary components — Course Content and Mathematical Practices. As you progress through the course, you will learn the essential mathematical practices through the course content. Together, these components prepare you to build a solid foundation in Calculus AB and hprepare you for success on the exam. The course content is further divided into units. Each unit is based on the three big ideas that provide the foundation upon which the course is structured.
Before you starting AP Calculus AB, it’s important to know the skills you’ll need to succeed. Prerequisite high school courses include Algebra, Geometry, Trigonometry, and Precalculus. These classes will help you develop reasoning skills with algebraic symbols and structures—key foundations for mastering Calculus.
Additionally, an AP Calc AB prep course can strengthen your foundation, making the class more manageable and boosting your confidence for the challenging AP Calculus AB exam.
AP Calculus AB’s Three Big Ideas
The curriculum for this course revolves around three AP Calculus AB key concepts or big ideas that provide the foundation upon which the course is structured. As you progress through the Cal AB course, you’ll find that each of these key concepts is interwoven into the course units. Let’s take a look at what these big ideas include:
- BIG IDEA 1: Change (CHA)
Using derivatives to describe rates of change of one variable with respect to another or using definite integrals to describe the net change in one variable over an interval of another, allows you to understand the concept of ‘change’ in a variety of contexts. The first big idea of Change (CHA) helps you to understand the relationship between integration and differentiation as expressed in the Fundamental Theorem of Calculus.
- BIG IDEA 2: Limits (LIM)
The second idea of Limits (LIM) teaches you to understand essential ideas, definitions, formulae, and theorems in calculus: for example, continuity, differentiation, and integration.
- Differentiation: Defining the derivative of a function, estimating derivatives at a point, connecting differentiability and continuity, determining derivatives of constants, sums, differences, constant multiples, and trigonometric functions. You’ll also need to learn about composite, implicit, and inverse Functions.
- Integration: Finding the average value of a function, applying accumulation functions, finding the area between curves of functions, and determining volumes from cross-sections and revolutions. You’ll also need to study the Fundamental Theorem of Calculus, finding anti-derivatives and indefinite integrals, and integrating using substitutions.
- BIG IDEA 3: Analysis Of Functions (FUN)
Understanding and analyzing the behaviors of functions by relating limits to differentiation, integration, and infinite series and relating each of these concepts to the others.
These three big ideas are spread across 8 units to help students learn each concept step by step. Together, the big ideas and the units form the structure of the Calculus course, similar to how college courses and textbooks are organized. Let’s go through each of the 8 units to see how they work together to build a strong understanding of Calculus.
The Eight AP Calculus AB Units and Their Topics
The AP Calculus AB units contain the course material you’ll learn throughout your AP classes. Based on what you study in these units, the AP Calculus AB exam will test you with 45 multiple-choice questions (MCQs) and six free-response questions (FRQs).
Remember the AP Calculus AB key concepts or big ideas that we talked about earlier on this page? As we outline each AP Calculus AB unit, we will also see which of those big ideas spiral across the course units. Each of the eight units comes with specific topics you’ll learn during your course.
Understanding how these AP Calculus AB topics are categorized will help you focus on them in detail. It will also help you identify your strengths and weaknesses, so you know exactly which unit and topic to work on during your revision. We’ve also included the relative exam weight for every unit, so you get all the info in one place. If you’re curious about any particular AP Calculus AB unit, click on the unit widgets below to learn more!
UNIT 1: Limits and Continuity
Exam Weightage: 10-12 % | Class periods ~ 22-23
This unit introduces you to the idea of change, which is the reason we study calculus. Calculus allows us to generalize knowledge about motion and apply it to diverse problems involving change. Using the concept of limits, you’ll learn the subtle distinction between evaluating a function at a point and considering what value the function is approaching after a point in time. As you move through this unit, you’ll learn how to determine change by justifying claims about limits and continuity through definitions, theorems, and properties.
The big ideas explored in this unit:
- Big Idea 1: Change – Can change occur in an instant?
- Big Idea 2: Limits – How does knowing the value of a limit, or that a limit does not exist, help you to make sense of interesting features of functions and their graphs?
- Big Idea 3: Analysis Of Functions – How do we close loopholes so that a conclusion about a function is always true?
In this unit, you will learn:
- How the average rate of change of a function can closely approximate the rate of change at an instant: Topic 1.1.
- What a limit is, how to express it, and how to calculate or approximate it from a table, graph, or function: Topics 1.2 – 1.4.
- Properties of limits and how to simplify them with algebra and trigonometry: Topics 1.5 – 1.7, 1.9.
- How limits of known functions can provide information about an unknown function using the squeeze theorem: Topic 1.8.
- What continuity is and how to identify when a function or graph is discontinuous at a point or over an interval: Topics 1.10 – 1.13.
- How to find infinite limits and limits at infinity, and what information these limits can provide about a function’s asymptotes: Topics 1.14 – 1.15.
- How continuity can prove the existence of a function value using the intermediate value theorem: Topic 1.16.
UNIT 2: Differentiation: Definition and Fundamental Properties
Exam Weightage: 10-12 % | Class periods ~ 13-14
This unit will develop your concept of differentiation, and how it is used to determine instantaneous rates of change. You will also learn to use a graphing calculator and explore how its various operations affect slopes of tangent lines. This exercise will help you develop a solid grasp of the basic rules and properties of differentiation.
The big ideas explored in this unit:
- Big Idea 1: Change – How can a state determine the rate of change in high school graduates at a particular level of public investment in education (in graduates per dollar) based on a model for the number of graduates as a function of the state’s education budget?
- Big Idea 2: Limits – Why do mathematical properties and rules for simplifying and evaluating limits apply to differentiation?
- Big Idea 3: Analysis Of Functions – If you knew that the rate of change in high school graduates at a particular level of public investment in education (in graduates per dollar) was a positive number, what might that tell you about the number of graduates at that level of investment?
In this unit, you will learn about the following AP Calculus AB topics:
- How to find an average rate of change using a difference quotient: Topic 2.1.
- What a derivative is, its relationship to an instantaneous rate of change, and how to calculate or estimate it using the limit of a difference quotient or a table: Topics 2.2 – 2.3.
- How continuity and differentiability are related: Topic 2.4.
- How to calculate the derivative of different families of functions: Topics 2.5, 2.7, 2.10.
- Properties of derivatives and advanced differentiation techniques: Topics 2.6, 2.8 – 2.9.
UNIT 3: Differentiation: Composite, Implicit, and Inverse Functions
Exam Weightage: 9-13% | Class periods ~ 10-11
In this unit, you’ll learn how to differentiate composite functions using the chain rule and apply that understanding to determine derivatives of implicit and inverse functions. The unit revolves around the principle that for composite functions, y is a function of u while u is a function of x. This unit is one of the most important units in the AP Calculus course, as mastering the chain rule is essential to your success in all future units.
The big ideas explored in this unit:
- Big Idea 3: Analysis Of Functions – If pressure experienced by a diver is a function of depth and depth is a function of time, how might we find the rate of change in pressure with respect to time?
- More advanced differentiation techniques: Topics 3.1 – 3.5.
- How to differentiate a function multiple times: Topic 3.6.
UNIT 4: Contextual Applications of Differentiation
Exam Weightage: 10–15% | Class periods ~ 10-11
Unit 4 begins by understanding average and instantaneous rates of change in problems involving motion. The unit then identifies differentiation as a common underlying structure to build an understanding of change in various contexts. You’ll also learn to apply L’Hopital’s Rule to determine limits of indeterminate forms.
The big ideas explored in this unit:
- Big Idea 1: Change – How are problems about position, velocity, and acceleration of a particle in motion over time structurally similar to problems about the volume of a rising balloon over an interval of heights, the population of London over the 14th century, or the metabolism of a dose of medicine over time?
- Big Idea 2: Limits – Since certain indeterminate forms seem to actually approach a limit, how can we determine that limit, provided it exists?
In this unit, you will learn about the following AP Calculus AB topics:
- What the derivative means in a real-world context: Topic 4.1 – 4.3.
- How to calculate a rate of change when two or more rates are related: Topic 4.4 – 4.5.
- How to approximate values of a function using a line tangent to the function at a nearby x-value: Topic 4.6.
- How to efficiently calculate difficult limits with L’Hopital’s Rule: Topic 4.7.
UNIT 5: Analytical Applications of Differentiation
Exam Weightage: 15-18% | Class periods ~ 15-16
This unit will focus on the analytical application of differentiation to obtain formal conclusions through reasoning, definitions, and theorems. You’ll learn to present justification for their conclusions about the behavior of functions over certain intervals or the locations of extreme values or points of inflection. The unit concludes this study of differentiation by applying abstract reasoning skills to justify solutions for realistic optimization problems.
The big ideas explored in this unit:
- Big Idea 3: Analysis Of Functions – How might the Mean Value Theorem be used to justify a conclusion that you were speeding at some point on a certain stretch of highway, even without knowing the exact time you were speeding?
- What additional information is included in a sound mathematical argument about optimization that a simple description of an equivalent answer lacks?
In this unit, you will learn about the following AP Calculus AB topics:
- How differentiability can prove the existence of a derivative value in an interval using the mean value theorem: Topic 5.1.
- What information the derivative can provide about the graph of a function like extreme values, intervals of increasing/decreasing, points of inflection, and intervals of concavity: Topics 5.2 – 5.9.
- How to use the derivative to optimize a quantity within a context: Topics 5.10 – 5.11.
- How implicit differentiation can provide information about a relation: Topic 5.12.
UNIT 6: Integration and Accumulation of Change
Exam Weightage: 17-20% | Class periods ~ 18-20
This unit is one of the most important units in the AP Calculus AB course. In this unit, you’ll learn the relationship between differentiation and integration using the Fundamental Theorem of Calculus. Just as differentiation determines instantaneous rate of change at a point, integration determines the accumulation of change over an interval. This unit forms the foundation for future units in this course because you’ll have to deploy the concept of Integration to various realistic and geometric applications.
The big ideas explored in this unit:
- Big Idea 1: Change – Given information about a rate of population growth over time, how can we determine how much the population changed over a given interval of time?
- Big Idea 2: Limits – If compounding more often increases the amount in an account with a given rate of return and term, why doesn’t compounding continuously result in an infinite account balance, all other things being equal?
- Big Idea 3: Analysis Of Functions – How is integrating to find areas related to differentiating to find slopes?
In this unit, you will learn:
- What a definite integral is, its relationship with accumulation of change and area, and how to approximate the area under a curve with Riemann sums: Topics 6.1 – 6.5.
- Properties of definite integrals: Topics 6.6 – 6.7.
- What an antiderivative is and its relationship with indefinite integrals: Topic 6.8.
- Advanced integration techniques: Topics 6.9 – 6.10, 6.14.
Note: Topics 6.11 – 6.13 are taught in the Calculus BC course.
UNIT 7: Differential Equations
Exam Weightage: 6-12% | Class periods ~ 8-9
In this unit, you’ll learn to set up and solve separable differential equations. This unit will teach you to translate mathematical information from one representation to another by matching equations and slope fields, rewriting verbal statements as differential equations, and sketching slope fields that match their symbolic representations.
The big ideas explored in this unit:
- Big Idea 3: Analysis Of Functions – How can we derive a model for the number of computers, C, infected by a virus, given a model for how fast the computers are being infected, dC dt , at a particular time?
In this unit, you will learn:
- How to model a context with a differential equation: Topics 7.1 – 7.2.
- How to use a slope field to estimate solutions to differential equations: Topics 7.3 – 7.4.
- How to find a general or particular solution to a differential equation: Topics 7.6 – 7.7.
- How to model exponential growth or decay with a differential equation and how to solve it: Topic 7.8.
Note: Topics 7.5 and 7.9 are taught in the Calculus BC course.
UNIT 8: Applications of Integration
Exam Weightage: 10–15% | Class periods ~ 19-20
This unit teaches you to find the average value of a function, model particle motion, and net change, and determine areas and volumes defined by graphs and functions. This unit also involves geometric applications of integration. The aim of this unit is to develop an understanding of Integration that can be transferred across these and many other applications.
The big ideas explored in this unit:
- Big Idea 1: Change – How is finding the number of visitors to a museum over an interval of time based on information about the rate of entry similar to finding the area of a region between a curve and the x-axis?
In this unit, you will learn:
- How to use a definite integral to find the average value of a function on an interval: Topic 8.1.
- What the definite integral means in a context: Topics 8.2 – 8.3.
- How to use a definite integral to find the area between curves: Topics 8.4 – 8.6.
- How to use a definite integral to find the volume of a solid with a cross-section of a particular geometric shape: Topics 8.7 – 8.8.
- How to use a definite integral to find the volume of a solid of revolution: Topics 8.9 – 8.12.
Note: Topic 8.13 is taught in the Calculus BC course.
Mathematical Practices for AP Calculus AB
The AP Calculus AB Mathematical Practices describe the skills you should acquire while exploring the Calc AB course units. There are 4 Mathematical Practices, and they form the core skills you need to develop to succeed in the exam. The AP Calculus AB course should enable you to integrate content with the practices mentioned below. With sufficient repetition and revision, you’ll be able to transfer these skills to the AP exam. Now, let's look at how the College Board® categorizes these core Mathematical Practices:
-
Implementing Mathematical Processes
This is the first practice you will learn during the AP Calculus AB course. As the name suggests, this Mathematical Practice will help you determine expressions and values using mathematical procedures and rules, and teach you how to implement those rules to solve problems.
-
Connecting Representations
This Mathematical Practice will teach you to translate mathematical information from a single representation or across multiple representations.
-
Justification
Justifying how you deduce the solution to a mathematical problem is crucial for the Free-Response Section of the AP Calculus AB exam. This Mathematical Practice will equip you with reasoning skills to logically establish the steps required to solve problems.
-
Communication and Notation
Understanding and solving a problem are not enough. You also need to know the correct way to communicate it. With the help of this Mathematical Practice, you’ll learn to use correct notation, language, and mathematical conventions to communicate results or solutions.
“Remember to apply the core skills and Mathematical Practices you learned during your course content. Developing a clear understanding of the concepts and theorems and mastering the skill to apply those concepts effortlessly is the key to unlocking that 5 on your AP Calculus AB exam!”
As you journey through each AP Calculus AB concept and topic, remember to go back and review the big ideas that each of these units encompasses. Knowing the fundamentals of a subject is the core of a solid learning process.
Preparing for your AP Calculus AB exam? Our course is thoughtfully designed to provide the perfect balance of learning and practice for your success. With our Watch, Read, Practice method, you’ll enjoy engaging video lessons that break down each topic, study guide materials that simplify tough concepts, and exam-like practice questions to refine your skills. Plus, our digital performance tracking ensures you stay focused on the areas that matter most. Start your AP Calculus AB journey today and see the difference!
Frequently Asked Questions
What are the most important topics in AP Calculus AB?
Below is a list of the most recurring AP Calc AB topics, based on their weight in the exam:
- (17-20%) Unit 6: Integration and Accumulation of Change
- (15-18%) Unit 5: Analytical Applications of Differentiation
- (10-15%) Unit 4: Contextual Applications of Differentiation
- (10-15%) Unit 8: Applications of Integration
- (10-12%) Unit 1: Limits and Continuity
- (10-12%) Unit 2: Differentiation: Definition and Fundamental Properties
What is the hardest unit topic in AP Calculus AB?
The hardest unit topics in the AP Calculus AB exam are primarily Unit 5: Analytical Applications of Differentiation and Unit 6: Integration and Accumulation of Change. These units not only carry the highest weight on the exam but also present significant conceptual challenges.
References
- AP Calculus AB. (n.d.). apcentral.collegeboard.org. Retrieved December 10, 2024, from https://apcentral.collegeboard.org/courses/ap-calculus-ab
- AP Calculus AB Course Overview. (2020). apcentral.collegeboard.org. Retrieved December 10, 2024, from https://apcentral.collegeboard.org/media/pdf/ap-calculus-ab-course-overview.pdf
- AP Calculus AB and BC Course and Exam Description. (2020). apcentral.collegeboard.org. Retrieved December 10, 2024, from https://apcentral.collegeboard.org/media/pdf/ap-calculus-ab-and-bc-course-and-exam-description.pdf
Read More About AP Calculus AB
How to Study for AP Calculus AB
Everything you need to know about the AP Calculus AB course content! Here’s our thorough study plan from our expert educators and score 5 effortlessly.
Are you curious about the AP Calculus AB exam format? This guide offers you a detailed break-up of the exam format, types of questions on the exam, and more!
Wondering how AP Calculus AB scoring works? Visit our article on scoring and score distribution—including the minimum score requirements for colleges.
How to Self Study for AP Calculus AB
Want to ace AP Calculus AB on your own? Follow this expert self-study guide with tips, tricks, and tools to prepare effectively for the exam.
Best AP Calculus AB Study Guide Comparison
Compare the best AP Calculus AB study guides! See how Kaplan, Barron's, and Princeton Review stack up against UWorld for comprehensive exam prep.
Best AP Calculus AB Prep Course Comparison
Searching for top AP Calculus AB prep courses? Read this review to compare the best courses and choose the perfect one for your success.