The AP Calculus AB exam consists of two major sections: multiple-choice questions (MCQs) and free-response questions (FRQs). The FRQ section of the AP Calculus AB exam is split into Part A and Part B. Part A consists of 2 free-response questions that you are allowed to use a calculator on and get 30 minutes to complete. Part B consists of 4 free-response questions that you cannot use a calculator on. You get 1 hour for this part. Questions in each part are weighted the same.
The entire free-response section accounts for 50% of the total points on the exam. Questions cover the 8 units of the AP Calculus AB course:
- Unit 1: Limits and Continuity
- Unit 2: Differentiation: Definition and Fundamental Properties
- Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
- Unit 4: Contextual Applications of Differentiation
- Unit 5: Analytical Applications of Differentiation
- Unit 6: Integration and Accumulation of Change
- Unit 7: Differential Equations
- Unit 8: Applications of Integration
| Section II | Part A | Part B |
|---|---|---|
| No. of Questions | 2 FRQs | 4 FRQs |
| Exam Weight | 16.7% | 33.3% |
| Time Allotted | 30 minutes | 1 hour |
| Calculator Usage | Permitted | Not Permitted |
How to Answer AP Calculus AB Free-Response Questions
Here are some tips for approaching the FRQ section of the AP Calculus AB exam:
- Read all the questions thoroughly. As you read through test questions, you will notice concepts that you are more familiar with. Answer these first to get them out of the way, build your confidence, and give you more time to focus on questions you may struggle with.
- Underline important information. When reading through the question stem, underline vocabulary, given values, function definitions, and any quantities the question asks for. This will help you key in on the important aspects of the question. Analyze vocabulary words thoroughly. For example, if a question says “relative maximum,” think about what that means in terms of calculus, like “derivative equals 0 and changes sign from positive to negative,” and “second derivative is negative.”
- Treat each part of every FRQ independently. Some parts of the questions are related to each other. For example, in Part A, they may ask you to estimate a Riemann sum, then in Part B to interpret whether your answer in Part A is an overestimate or underestimate. Even if you are not confident in your response to Part A, answer Part B. Readers are instructed to grade every answer independently, so you can still get full points on Part B even if your answer to Part A is incorrect but you interpreted it correctly.
- Organize your work. As you prepare for the exam, use the College Board® scoring guidelines to study. When you answer questions on the exam, only include the information requested to score points. If you need to jot down your thoughts as you work toward an answer, do so in the question booklet.
- Don’t erase. If you make an error, do not erase it. Instead, draw a line or X through the sections you don’t want the readers to consider. This saves time and keeps your work organized.
- Don’t simplify. Leave your answers in their complicated form unless a question explicitly tells you to simplify or give a numerical answer. By understanding the scoring guidelines and studying the College Board’s sample questions, you will get a better idea of when you should or should not simplify your answers.
- Don’t overwork on Part A. The College Board expects your graphing calculator to have these functionalities that you can use in Part A:
- Plot the graph of a function within an arbitrary viewing window.
- Find the zeros of functions when solving equations numerically.
- Calculate the derivative of a function numerically.
- Calculate the value of a definite integral numerically.
You do not have to show any intermediate steps for Part A FRQs. Simply show the set up correctly, plug it into your calculator, and give the numerical answer.
- Return to Part A. If you have time to review your answers to Part A questions after finishing Part B, you will not be allowed access to your calculator. Should you notice an error in setting up an integral or equation, fix it even if you can’t calculate the result without a calculator. You may get points for the correct setup even without the correct numerical answer.
To dive deeper into mastering AP Calculus, an AP Calculus Study Guide can help you consolidate your knowledge. Available in both print and e-book formats, this comprehensive guide provides step-by-step explanations to prepare for every part of the exam, including the free-response section.
AP Calculus AB Free-Response Question Examples
Here are some examples of AP Calc AB FRQs from past exams to illustrate the different kinds of questions you will see on the exam. These questions come directly from the College Board. For a more structured approach to mastering the AP Calculus AB exam, consider enrolling in an AP Calc AB Prep Course. This course breaks down key concepts and prepares you with guided lessons, video lessons, practice tests, and time management tips to boost your performance.
One of the question types that appears most frequently on the AP Calculus AB exam is a table of data modeling a real-world scenario. The table tests concepts that allow you to calculate approximate values such as average rate of change and Riemann sums. The intermediate value theorem is another concept that is tested with tabular data. An example of this type of question (#4 from 2022) is shown below, with highlights demonstrating these common elements.
| t (days) |
0 | 3 | 7 | 10 | 12 |
| r ' (t ) (centimeters per day) |
−6.1 | −5.0 | −4.4 | −3.8 | −3.5 |
An ice sculpture melts in such a way that it can be modeled as a cone that maintains a conical shape as it decreases in size. The radius of the base of the cone is given by a twice-differentiable function r , where r (t ) is measured in centimeters and t is measured in days. The table above gives selected values of r' (t ), the rate of change of the radius, over the time interval 0 ≤ t ≤ 12.
- Approximate r'' (8.5) using the average rate of change of r' over the interval 7 ≤ t ≤ 10. Show the computations that lead to your answer, and indicate units of measure.
- Is there a time t, 0 ≤ t ≤ 3, for which r' ( t ) = −6 ? Justify your answer.
- Use a right Riemann sum with the four subintervals indicated in the table to approximate the value of ∫120 r' (t ) dt.
- The height of the cone decreases at a rate of 2 centimeters per day. At time t = 3 days, the radius is 100 centimeters and the height is 50 centimeters. Find the rate of change of the volume of the cone with respect to time, in cubic centimeters per day, at time t = 3 days. (The volume V of a cone with radius r and height h is V = 1⁄3 πr 2h. )
Reference: College Board: https://secure-media.collegeboard.org/apc/ap22-frq-calculus-ab.pdf
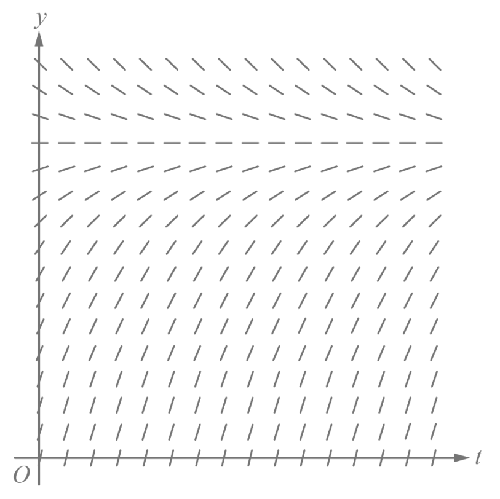
Another commonly asked free-response question tests whether you understand a meaning within a context. You will be asked to calculate a quantity and give an interpretation of what that quantity means within the given scenario. You will have to present your inference with the correct units, requiring you to understand how a derivative or integral changes the units of a function. This often occurs within a table question. The question below (2021 #6) is an example. Also shown in Part A is a slope field from Unit 7, a commonly tested concept in AP Calculus AB FRQs.
A medication is administered to a patient. The amount, in milligrams, of the medication in the patient at time t hours is modeled by a function y = A(t ) that satisfies the differential equation dy⁄dt = 12 − y⁄3. At time t = 0 hours, there are 0 milligrams of the medication in the patient.
- A portion of the slope field for the differential equation dy⁄dt = 12 − y⁄3 is given below. Sketch the solution curve through the point (0, 0).
- Using correct units, interpret the statement lim t→∞ A (t ) = 12 in the context of this problem.
- Use separation of variables to find y = A (t ), the particular solution to the differential equation dy⁄dt = 12 − y⁄3 with initial condition A (0) = 0.
- A different procedure is used to administer the medication to a second patient. The amount, in milligrams, of the medication in the second patient at time t hours is modeled by a function y = B (t ) that satisfies the differential equation dy⁄dt = 3 − y⁄t + 2. At time t = 1 hour, there are 2.5 milligrams of the medication in the second patient. Is the rate of change of the amount of the medication in the second patient increasing or decreasing at time t = 1 ? Give a reason for your answer.
Reference: College Board: https://apcentral.collegeboard.org/pdf/ap21-frq-calculus-ab.pdf
Another question tests your ability to interpret data from a number of different presentations: functions, graphs, and tables. The question below (2022 #2) shows a graph of a function and asks about area and volume from Unit 8 and related rates from Unit 4. Related rates showed up twice in 2022, once in #2c below and again in #4d (shown above).
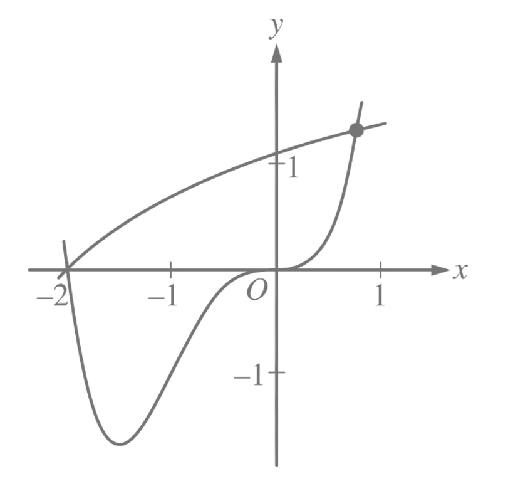
1. Let ƒ and g be the functions defined by ƒ(x ) = ln (x + 3) and g (x ) = x4 + 2x3. The graphs of ƒ and g, shown in the figure above, intersect at x = −2 and x = B, where B > 0.
- Find the area of the region enclosed by the graphs of ƒ and g .
- For −2 ≤ x ≤ B, let h (x ) be the vertical distance between the graphs of ƒ and g . Is h increasing or decreasing at x = −0.5 ? Give a reason for your answer.
- The region enclosed by the graphs of ƒ and g is the base of solid. Cross sections of the solid taken perpendicular to the x -axis are squares. Find the volume of the solid.
- A vertical line in the xy - plane travels from left to right along the base of the solid described in part (c). The vertical line is moving at a constant rate of 7 units per second. Find the rate of change of the area of the cross section above the vertical line with respect to time when the vertical line is at position x = −0.5.
Reference: College Board: https://apcentral.collegeboard.org/pdf/ap22-frq-calculus-ab.pdf
How Can I Practice AP Calculus AB Free-Response Questions?
The best way to practice for the AP Calculus AB exam is to use the College Board's previous exams. Whether you’re learning and practicing in your AP class or studying on your own, prioritize using the most recent exams because the College Board changes how it asks questions over time. Use the scoring guidelines to grade yourself. Study the rubrics that the College Board provides. After taking a few sections, start timing yourself so you’re prepared for the exam day experience.
To practice effectively and identify your strengths and weaknesses, using an AP Calculus Question Bank will provide a wide range of questions from past exams and detailed answer explanations. It’s a great tool for exam-like practice that builds confidence.
Frequently Asked Questions
How are the AP Calculus AB free-response questions graded?
How long is the FRQ section of the AP Calculus AB exam?
Where can I get FRQs from past AP Calculus AB past exams?
References
- AP Calculus AB. (n.d.). Collegeboard.org. Retrieved March 12, 2024, from https://apcentral.collegeboard.org/courses/ap-calculus-ab
- AP Calculus AB Course Overview. (2021). Collegeboard.org. Retrieved March 12, 2024, from https://apcentral.collegeboard.org/media/pdf/ap-calculus-ab-course-overview.pdf
- AP Calculus AB and BC Course and Exam Description. (2020). Collegeboard.org. Retrieved March 12, 2024, from https://apcentral.collegeboard.org/media/pdf/ap-calculus-ab-and-bc-course-and-exam-description.pdf
- Chief Reader Report on Student Responses: 2023 AP Calculus AB/BC Free-Response Questions. (2023). Collegeboard. Retrieved March 12, 2024, from https://apcentral.collegeboard.org/media/pdf/ap23-cr-report-calculus.pdf
- AP® Calculus AB Scoring Guidelines. (2023). Collegeboard. Retrieved March 12, 2024, from https://apcentral.collegeboard.org/media/pdf/ap23-sg-calculus-ab.pdf
Related Topics
How to Approach AP Calculus AB MCQs
Answering MCQs appears simple, but a correct answer can differ by a small margin. Here’s how to approach the right answer on AP Calculus AB MCQs.
AP Calculus AB Study Plan & Tips
Whether you want to get a head start this summer or wish to wait until 2 weeks before the exam to prep, we provide tips to help you study.
Preparing for AP Calculus AB? Get thorough exam information including what’s on the exam, why to take it, prerequisites, and the difficulty level.
How to Self Study for AP Calculus AB
Want to ace AP Calculus AB on your own? Follow this expert self-study guide with tips, tricks, and tools to prepare effectively for the exam.
Best AP Calculus AB Study Guide Comparison
Compare the best AP Calculus AB study guides! See how Kaplan, Barron's, and Princeton Review stack up against UWorld for comprehensive exam prep.
Best AP Calculus AB Prep Course Comparison
Searching for top AP Calculus AB prep courses? Read this review to compare the best courses and choose the perfect one for your success.