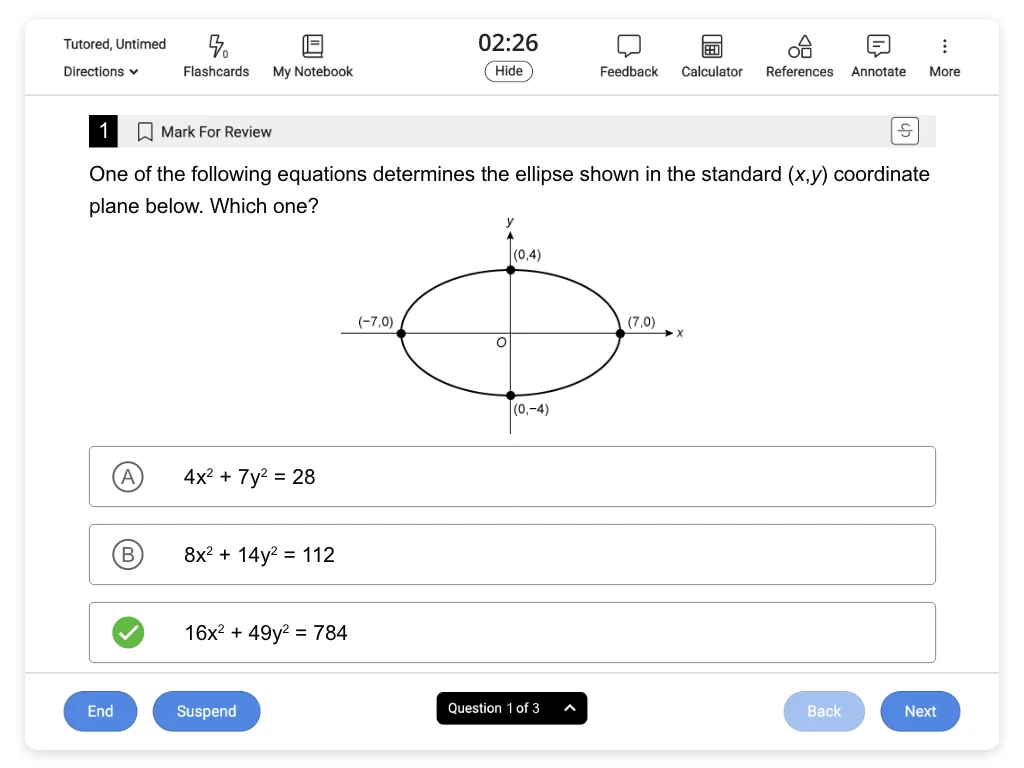
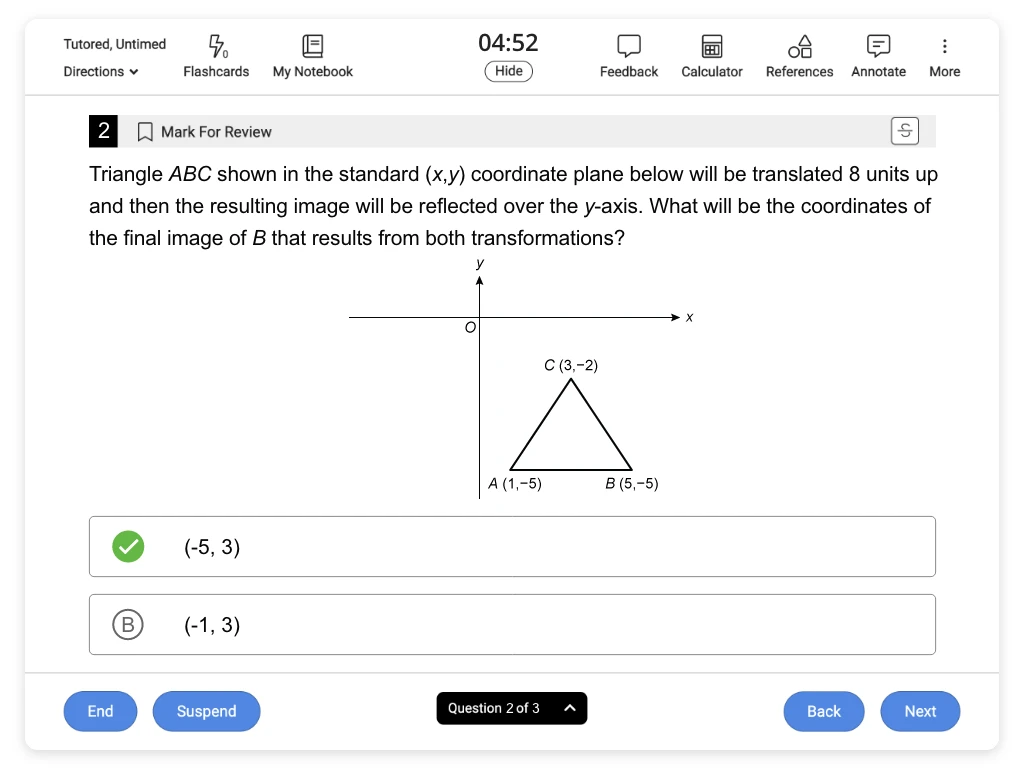
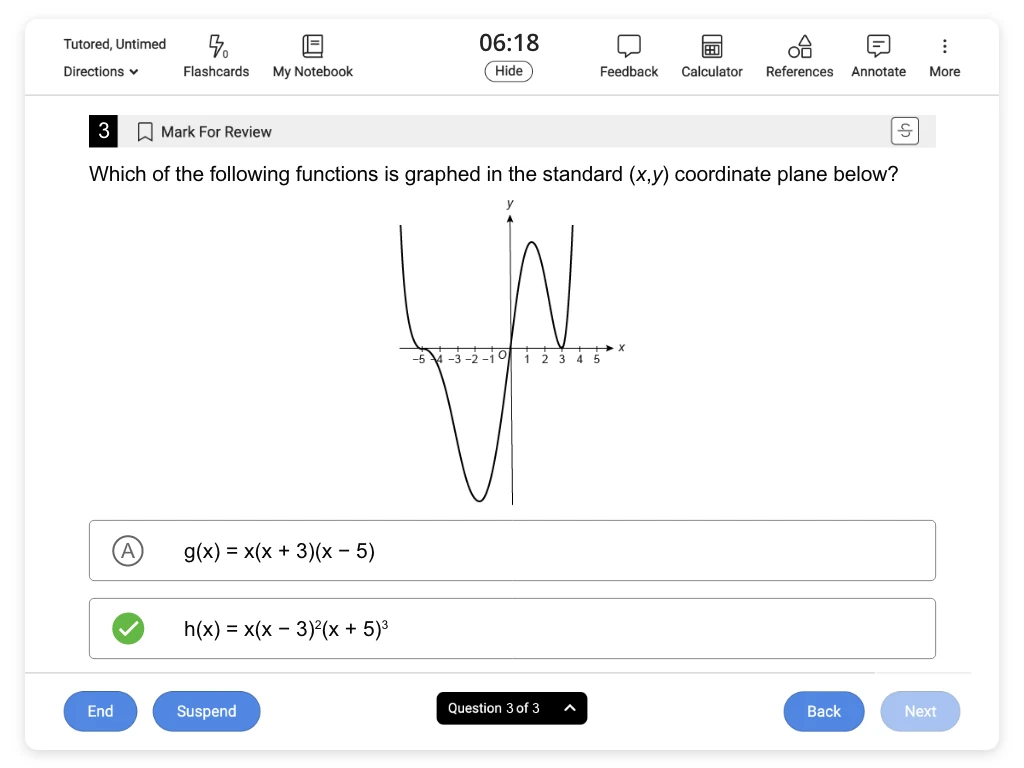
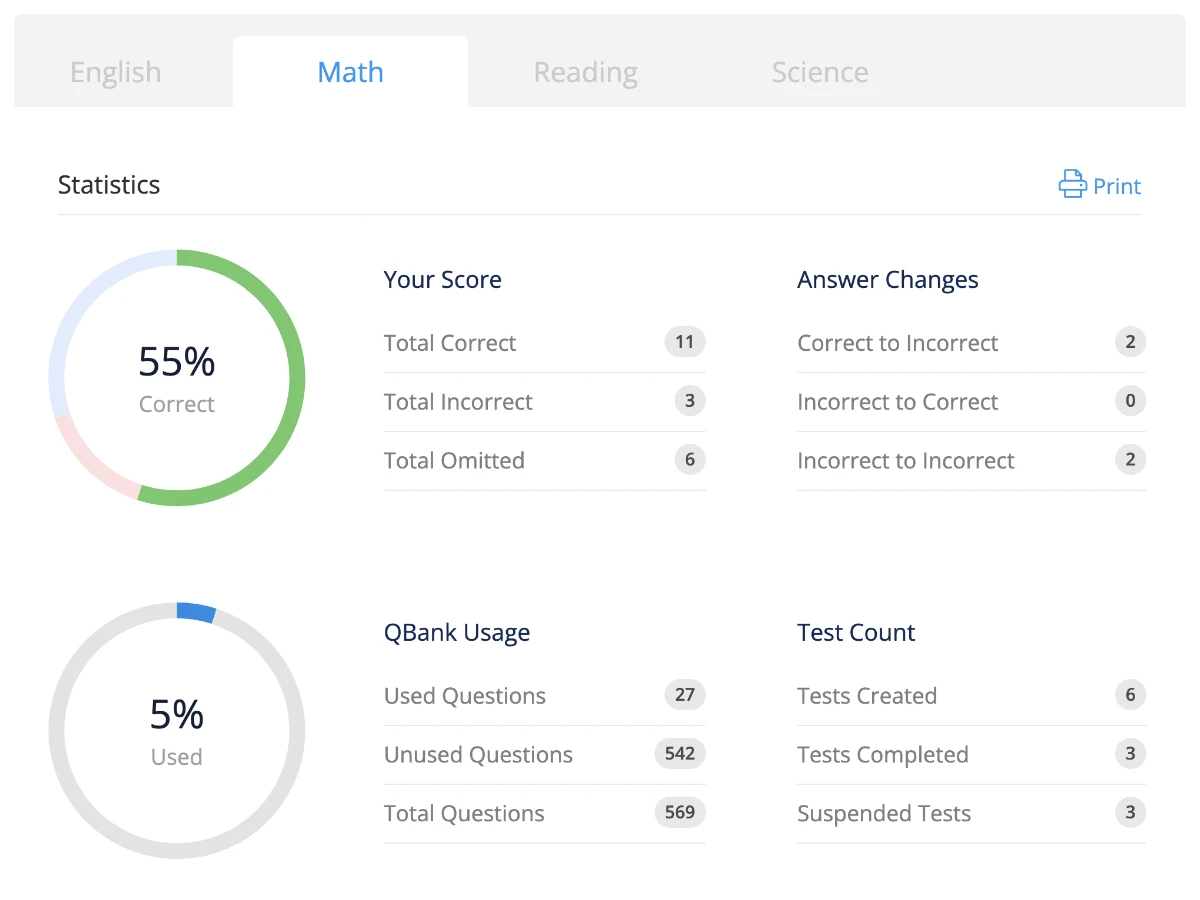
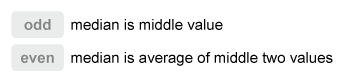Sample ACT® Math Problems & Questions
No Credit Card Required
Free Sample ACT Math Problems
Question
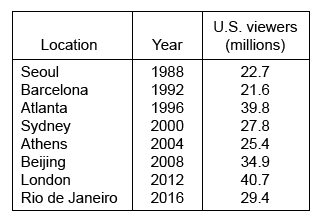
The Summer Olympic Games are among the most-watched internationally televised sporting events and have been held in over 20 different countries. The table below gives the number of U.S. viewers, in millions, for 8 Summer Olympics opening ceremonies located in different international cities.
What is the median number of viewers, in millions, of these 8 Summer Olympics opening ceremonies?
| A. 26.6 | |
| B. 27.8 | |
| C. 28.6 | |
| D. 30.2 |
Hint :
The median is the middle of a numerically ordered data set. When the number of values is odd, the median is the middle value. When it is even, the median is the average of the two middle values.
Explanation
The median of a data set with an even number of values is the average of the middle two values when all values are ordered numerically.
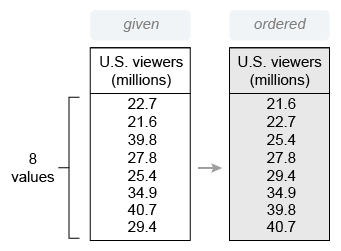
The given data set has 8 values, but the values are not in order. First order the number of U.S. viewers from least to greatest.
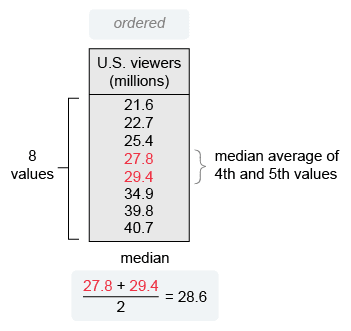
There are 8 values in the given table, so the median is the average of the 4th and 5th ordered numbers.
The median number of U.S. viewers of these 8 Summer Olympics opening ceremonies is 28.6 million.
(Choice A) 26.6 is the average of the middle two values of the unordered list of numbers of viewers. However, the median is the average of the middle two values when all values are ordered numerically.
(Choice B) 27.8 is the smallest of the middle two values of the ordered list of numbers of viewers. However, the median of a data set with an even number of values is the average of the middle two values.
(Choice D) 30.2 is the mean of the number of viewers. However, the question asks for the median of the number of viewers.
Things to remember:
The median is the middle value of a data set that is ordered numerically. When the number of values is odd, the median is the middle value. When it is even, the median is the average of the two middle values.
Question
A box contains 12 flavored candies: 5 lime, 4 cherry, 1 orange, and 2 grape. Which of the following expressions gives the probability of choosing, at random and without replacement, a cherry candy for the first choice, a lime candy for the second choice, and a cherry candy for the third choice?
| A.
|
|
| B.
|
|
| C.
|
|
| D.
|
Hint :
The probability that dependent events occur is equal to the probability that the first event occurs multiplied by the probability that each consecutive event occurs, given that each preceding event has already occurred.
Explanation
The candies are chosen without replacement (they are not replaced in the box after being chosen), so each event of choosing a candy affects the probability of the events that follow. Therefore, the events are dependent.
The probability that dependent events occur is equal to the probability that the first event occurs multiplied by the probability that each consecutive event occurs, given that each preceding event has already occurred.
The 1st event is that a cherry candy is chosen and not replaced in the box. The 2nd event is that a lime candy is chosen and not replaced, and the 3rd event is that a cherry candy is chosen and not replaced.
Therefore, the probability that a cherry candy is chosen first, a lime candy is chosen second, and a cherry candy is chosen third is:
Use the following formula to find the probability P of each event:
P(cherry 1st)
The first event is that a cherry candy is chosen first from the box.
The number of desired outcomes for choosing cherry is the number of cherry candies in the box.
The total number of possible outcomes for choosing cherry is the total number of candies in the box.
It is given that there are 4 cherry candies in the box, and it is given that the box contains a total of 12 candies. Therefore, the probability of choosing a cherry first is .
P(lime 2nd)
The probability that a lime candy is chosen second depends on the first event that a cherry candy is chosen, so it is the probability given that the first chosen candy is cherry.
The number of desired outcomes is the number of lime candies after a cherry candy is removed.
The number of possible outcomes is the number of candies remaining after a cherry candy is removed.
It is given that the full box had 5 lime candies. After a cherry candy is removed, there are still 5 lime candies and a total of 12 − 1 = 11 candies remaining.
Therefore, the probability of choosing a lime candy second is .
P(cherry 3rd)
The probability that a cherry candy is chosen third depends on the first event and the second event, so it is the probability given that the first chosen candy is cherry and the second chosen is lime.
The number of desired outcomes is the number of cherry candies remaining. The total number of possible outcomes is the number of candies remaining after a cherry and lime candy are removed.
It is given that the full box had 4 cherry candies. A cherry candy and then a lime candy were removed, so there are 4 − 1 = 3 cherry candies remaining and a total of 12 − 2 = 10 candies remaining.
Therefore, the probability of choosing a cherry candy third is .
P(cherry 1st, lime 2nd, and cherry 3rd)
Now multiply the individual probabilities to find the probability that all three events occur.
|
|
Probability of cherry 1st, lime 2nd, and cherry 3rd |
| Plug in probabilities |
The probability of choosing, at random and without replacement, a cherry candy first, a lime candy second, and a cherry candy third is .
(Choice A) may result from mistaking the total number of candies in the box to be 12 with each choice. However, the total number of candies in the box decreases by 1 each time a choice is made without replacement.
(Choice B) is the probability of choosing a cherry candy, a lime candy, and a cherry candy with replacement instead of without replacement.
(Choice C) may result from mistaking the number of cherry candies in the box for the third choice to be 4. However, the number of cherry candies in the box decreases by 1 each time a cherry candy is chosen without replacement.
Things to remember:
-
To find the probability of a single event, use the following formula:
-
Two events are dependent if one event affects the other.
-
To find the probability that two dependent events occur, multiply their individual probabilities together.
Question
For all real values of x, which of the following is the solution set of 3x + 9 ≥ −12 ?
| A. x ≤ −1 | |
| B. x ≥ −1 | |
| C. x ≤ −7 | |
| D. x ≥ −7 |
Hint :
To find the solution set of an inequality in one variable, isolate the variable by itself on one side of the inequality.
Explanation
The solution set of an inequality with one variable is the set of all values of the variable that make the inequality true. To find the solution set, solve for the variable in the inequality.
To solve for x in the given inequality 3x + 9 ≥ −12, subtract 9 from both sides and divide by 3 to isolate x so it is by itself on one side of the inequality.
| 3x + 9 ≥ −12 | |
| 3x ≥ −21 | Subtract 9 from both sides |
| x ≥ −7 | Divide both sides by 3 Note: The inequality sign remains unchanged because 3 is positive. |
Therefore, the solution set of the given inequality is x ≥ −7.
(Choice A) x ≤ −1 may result from a combination of the errors described in Choices B and C.
(Choice B) x ≥ −1 may result from incorrectly subtracting −12 − 9 to get −3 (instead of −21).
(Choice C) x ≤ −7 may result from mistakenly reversing the direction of the inequality. The inequality sign only reverses as a result of multiplying or dividing both sides by a negative number.
Things to remember:
- To find the solution set of an inequality in one variable, isolate the variable by itself on one side of the inequality.
- The solution set of an inequality is the set of all values that make the inequality true.
Question
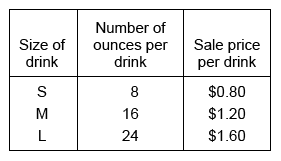
Bart's Burgers sells different sizes of drinks. The number of ounces and the sale price per drink for each of the 3 sizes are given in the table below. The sale price is the amount a customer pays for that drink.
The average sale price per ounce of a large (L) drink is closest to which of the following amounts?
| A. $0.07 | |
| B. $0.15 | |
| C. $0.20 | |
| D. $0.67 |
Hint :
Use the given table to identify the sale price and the number of ounces per large (L) drink.
Explanation
The average price per item is equal to the price of the items divided by the number of items.
The question asks for the average sale price per ounce of a large (L) drink.
The total price of the items is the price per L drink.
The total number of items is the ounces per L drink.
Identify from the given table that the price of an L drink is $1.60 and the number of ounces in an L drink is 24.
Plug these values into the formula above and divide to find the average sale price per ounce.
| Average sale price per ounce | |
| Plug in price and number of ounces | |
| Divide | |
| Round to match answer choices |
The average sale price per ounce of a large (L) drink is $0.07.
(Choice B) $0.15 may result from mistakenly dividing the number of ounces in a large drink by an incorrect price, but the average sale price per ounce is price divided by ounces.
(Choice C) $0.20 may result from mistakenly dividing the price of a large drink by the number of ounces in a small drink (instead of in a large drink).
(Choice D) $0.67 may result from a calculation error when dividing $1.60 by 24 to get $0.66… (instead of $0.066…).
Things to remember:
The average price per item is equal to the price of the items divided by the number of items.
Question
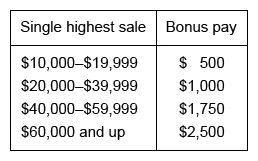
An electronics company has an incentive program in which account representatives can earn money based on their monthly sales. Representatives can earn bonus pay based on their single highest sale for the month.
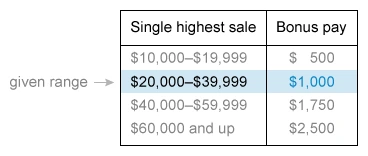
In a certain month, account representatives at the electronics company earned bonus pay that totaled $9,500. What is the maximum number of representatives whose single highest sale that month could have been in the range of $20,000–$39,999?
| A. 4 | |
| B. 5 | |
| C. 9 | |
| D. 10 |
Hint :
The maximum number of representatives whose single highest sale could have been in the given range is equal to the greatest whole number of bonuses for that range that could have been paid with the given total bonus.
Explanation
The number of representatives is equivalent to the number of bonuses paid, so find the maximum number of bonuses that could have been paid with the given total.
Divide the given total bonus pay by the bonus for a single highest sale in the range of $20,000–$39,999 to determine the maximum number of bonuses.
The given total bonus pay was $9,500.
To determine the bonus for a single highest sale in the range of $20,000–$39,999, use the given table.
The bonus for a single highest sale in the given range is $1,000.
Divide the given total bonus pay (9,500) by the bonus for each sale (1,000) to determine the maximum number of bonuses that could have been paid.
| Maximum number of bonuses | |
| Plug in values | |
| Divide |
The number of bonuses paid must be a whole number. The largest whole number less than 9.5 is 9, so the maximum number of bonuses that could be paid is 9.
Therefore, the maximum number of representatives is 9.
(Choices A and B) 4 and 5 may result from mistakenly dividing the highest value ($39,999) in the given range by the total bonus pay ($9,500).
(Choice D) 10 may result from mistakenly rounding 9.5 up to 10. However, the total bonus pay ($9,500) is not enough to pay a bonus of $1,000 to 10 representatives.
Get Exam-Ready with Exam-Like ACT Math Examples
Unlimited Exam-level Examples
Customized to Your Study Needs
Understand the “Why” Behind Every Answer
Score Free Sample ACT Problems Every Week!
Get ACT exam-ready with weekly exam-like questions sent to your inbox.
Boost Your ACT Math Score to a 36
“UWorld's question bank can be described in one word: revolutionary. It accurately models the content that you would see on the test and familiarizes you with the test through PRACTICE, not mindless reading of the content. After using UWorld's amazing question bank, I was able to score a 36. It's proven to work and yielded amazingly good results for me!”
- Ravi
Create Unlimited Sets of ACT Math Problems
- What if you could take the ACT Math as many times as you needed before it actually counted? Well, you can.
- Study formulas and hone your computational skills with as many ACT math examples.
- Customize by topic, custom tag, or even just questions you’ve previously gotten wrong.
Learn Why Each Answer is Right or Wrong
- Mathematical success comes from true understanding—not memorization. Each ACT Math example includes step-by-step reasoning and colorful visuals that simplify complex topics like functions, angles, and trigonometric relationships.
- Plus, you can save key examples to your personalized flashcards or digital notebook for review anytime.
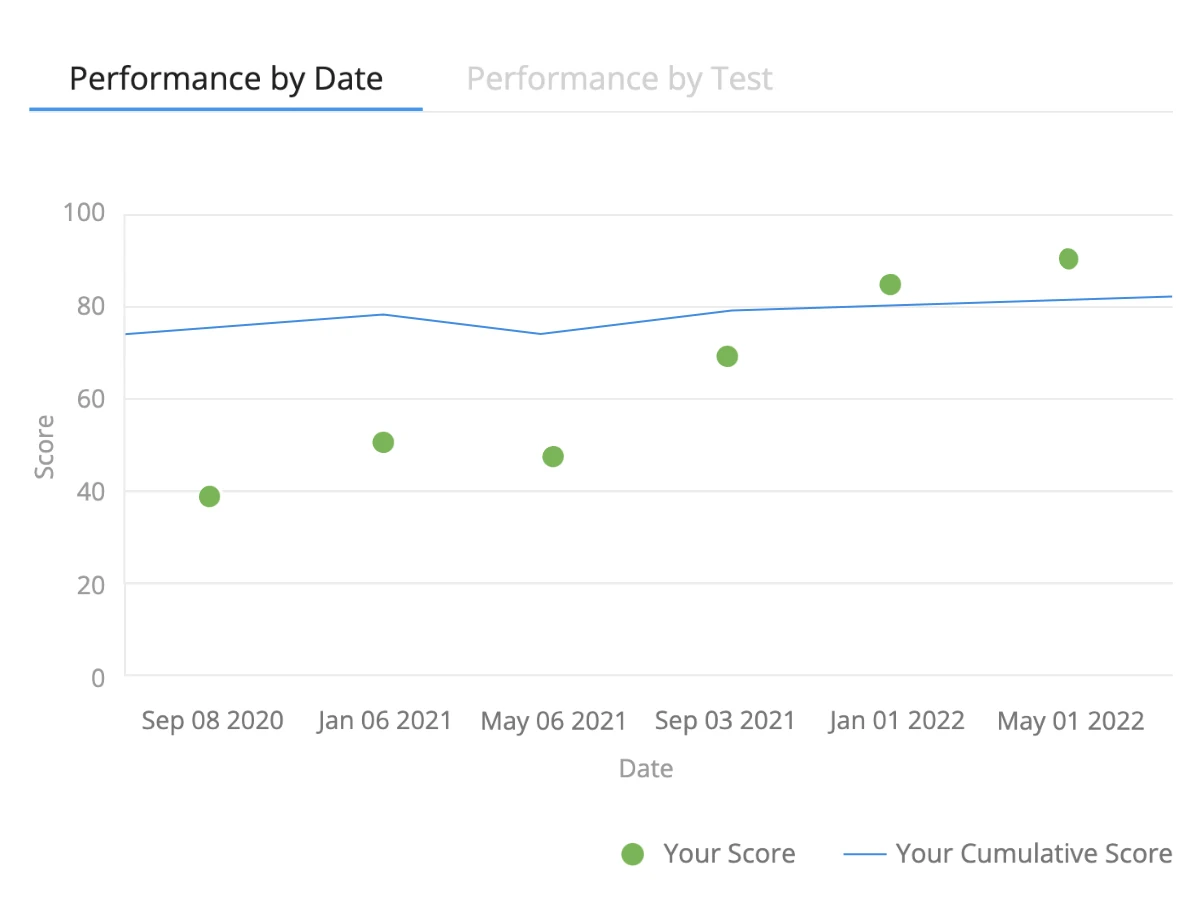
Track Your Progress With Smart Analytics
- Focus your energy where it counts. Our analytics dashboard tracks your accuracy across algebra, geometry, and trigonometry so you can measure growth over time.
- See your predicted ACT Math score, compare your results with peers, and adjust your study plan based on clear data-driven insights.
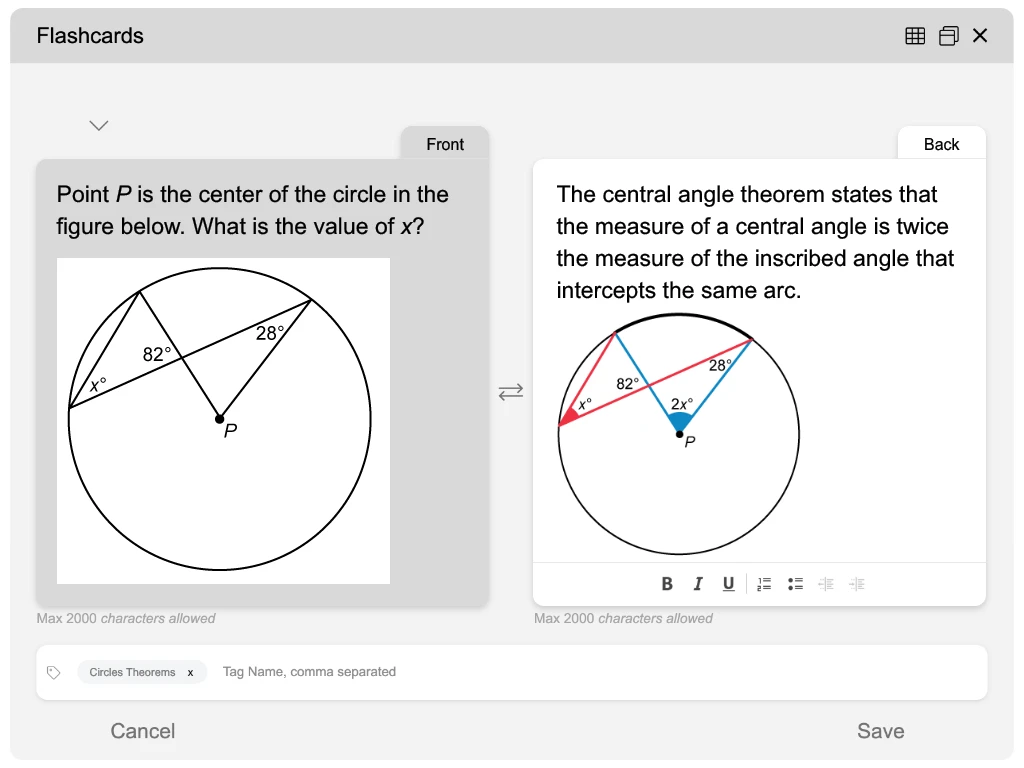
My Notebook & Flashcards: Study Made Simple
- Find a helpful explanation? Like a visualization of a formula? Just click, highlight, and select create notes or flashcards.
- It’s easy to transfer QBank visual and written content to your digital My Notebook and Flashcards and keep them all organized by topic or custom tag.
- The best part? It’s always in arms reach with our mobile app.
We make the real thing feel like practice
At UWorld, every ACT Math example is crafted to match the style and challenge of the actual exam. By studying in a realistic environment, you’ll walk into test day with confidence—it’ll feel like you’ve already done it before.
Hear from Our Happy Students
I got a 35 from studying using UWorld, it has the best question bank along with the most informative explanations.”
UWorld contributed to a 10 point increase for me on the ACT. The website was FANTASTIC for me to practice on the go. I especially liked the math section.”
The primary reason for me being extremely likely to recommend UWorld to a friend is because it has helped me prepare and achieve a 35 Composite ACT Score!