With 60 minutes to tackle 60 questions, every second counts. Since the ACT doesn't provide a comprehensive list of formulas, you must commit them to memory to improve your efficiency and ability to respond quickly and accurately to each question in the allotted time. Familiarizing yourself with math equations for the ACT is a crucial step in preparing for the test and ensuring you’re ready to tackle every question confidently.
Two advantages of the ACT over the SAT® are that you can use a calculator throughout the math section and there are fewer math questions. Consider practicing with materials specifically designed for the ACT to tackle the formula challenge. UWorld offers ACT practice exams and comprehensive resources to help you strengthen your prep time and master ACT math equations.
What Math Formulas You Must Know for the ACT
Practicing for the ACT math section is like gearing up for a big journey. To do well, you'll need a reliable map, which means knowing the essential formulas. By understanding key math equations for the ACT, you’ll improve your ability to solve problems efficiently and accurately.
Number and Quantity
- Arithmetic Sequences an = a1 + (n-1)d
- Geometric Sequences an = a1 . rn-1
- Logarithms If logb (x) = y, then by = x logb (xy) = logb (x) + logb (y) logb (x/y) = logb (x) - logb (y)
Functions
f ∘ g(x) = f(g(x))
This composition function, where the output of g(x) is the input for f(x). Notice that f ∘ g(x) is different from f g(x) = f(x) × g(x).
Algebra
d = rt
Statistics and Probability
- Percentages n % of m = n/100 × m
-
Mean, Median, Mode, and Range
The ACT tests basic statistical knowledge, often involving the following measures:
- Mean: the average
- Median: either the middle term or, in the case of an even number of terms, the average of the two middle terms
- Mode: the term that occurs most frequently.
- Range: the difference between the largest and smallest terms.
-
Probability
P(A) =number of desired outcomes total number of possible outcomes
- Independent Events P (A and B) = P (A) × P (B)
Geometry
-
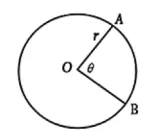
Circles
Area: A = πr2
Circumference: C = 2πr
Arc Length: L(A,B) =θ 360°× 2πrSector Area: AOB =Equation for circle with center (h, k) and radius: r2 = (x - h)2 + (y - k)2θ 360°× πr2 -
Lines
Slope of a Line: m =y2 - y1 x2 - x1Midpoint: M =(Distance: d = √(x2 - x1)2 + (y2 - y1)2x1 + x2 2,y1 + y2 2)
-
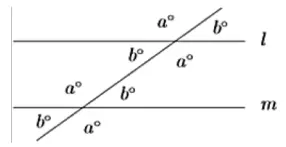
Angles
Sum of Interior Angles: S = 180(n - 2)°
Each Interior Angle =Sum of Exterior Angles = 360˚180(n-2)° nEach Interior Angle =360˚ n -
FOIL (First, Outer, Inner, Last)
(a + b) (c + d) = ac + ad + bc + bd
Below are few FOIL shortcuts to memorize, where y is a constant:
(x + y) (x + y) = (x + y)2 = x2 + 2xy + y2 (x - y) (x - y) = (x - y)2 = x2 - 2xy + y2 (x + y) (x - y) = (x2 - y2) -
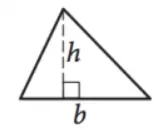
Area of a Triangle
Area: A =1 2bhThis equation gives the area of any triangle when you’re given the lengths of the base (b) and height (h). For equilateral triangles, where all 3 sides are the same length, the area equation is:
Area: A =s2 √3 4 -
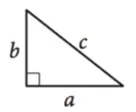
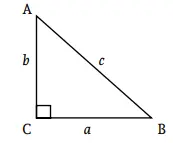
Pythagorean Theorem
As angles in a triangle always add up to 180°, a right triangle is defined as any triangle with one right angle, ensuring the other 2 angles are complementary. The side lengths of right triangles can be defined by the Pythagorean Theorem:
a2 + b2 = c2Here, a and b are the sides across the complementary angles. C is the hypotenuse, the side across from the right angle.
-
Areas
Parallelogram: A = bh
Trapezoid: A =Cube: A = 6s21 2(b1+ b2)h
-
Volume
Cube: V = s3
Rectangular Prism: V = lwh
Cylinder: V = πr2h
Sphere: V =4 3πr3
Trigonometry
Frequently Answered Questions (FAQs)
Do I get a formula sheet on the ACT?
No. Unlike the SAT, the ACT math section does not provide a general formula or reference sheet. Some uncommon concepts are explained in “notes” at the end of relevant questions (e.g., a question including factorials would indicate that 6! = 6(5)(4)(3)(2)(1), and a question involving acres as a unit of measurement would indicate that 1 acre = 43,560 feet).
Do I have to memorize formulas for the ACT?
Can I program formulas into my calculator for the ACT?
Read More Related Articles
Elevate your ACT Math game with expert tips. Dive into proven strategies for a successful performance. Enhance your understanding and conquer the math section with confidence.
About ACT Math SectionUncover the intricacies of the ACT Math section. Gain valuable insights for confidence on test day. Navigate through challenging topics, ensuring you're well-prepared for any mathematical scenario.
ACT SyllabusDecode the ACT syllabus for effective preparation. Uncover essential concepts to expect on the exam. Delve deeper into the syllabus, ensuring you grasp fundamental concepts crucial for success.
Free ACT Practice TestAccess a free ACT practice test. Sharpen your abilities and approach the exam with confidence. Utilize this invaluable resource to fine-tune your skills and gauge your readiness for the actual test.
