How to Solve ACT® Math Questions
Tricks and Strategies
Discover the keys to mastering ACT® Math with our guide on clever tricks and smart strategies. Whether you're figuring out Pre-Algebra, getting the hang of Trigonometry, or exploring extra math bits, this guide is here for you. Dive into easy-to-follow techniques, practical tips, and illustrative examples to enhance your ACT Math skills and confidently tackle any question.
How to Solve ACT Math Questions
Cracking the code of ACT Math demands a solid understanding of a variety of mathematical concepts, encompassing intricate algebraic equations and geometry challenges. Our guide is designed to equip you with practical tricks and strategies, ensuring preparedness for every question type, including Multiple-Choice Questions (MCQs). To reinforce your understanding, we've incorporated valuable ACT Math sample questions, allowing you to apply the learned strategies in a practical context.
Applicability to SAT Math
The strategies outlined in this guide are not confined to ACT Math; they are also applicable to SAT Math. Whether you're preparing for the ACT or SAT, the foundational skills covered here—such as algebraic problem-solving and geometry proficiency—are integral to success.
Pre-Algebra
Pre-algebra constitutes the fundamental building blocks of the ACT Math Test, likely familiar from your middle school math classes. While not conceptually challenging, these topics may contain nuances that could have slipped from memory. Since pre-algebra questions are not generally tricky, a thorough review should suffice to ensure accuracy and success.
- ACT Math questions include 14 pre-algebra items that cover math terminology, basic number theory, and the manipulation of fractions and decimals. Strengthen your understanding of these content areas with key insights from reliable ACT Math Pre-Algebra study materials.
To discover everything you need to know about the format, syllabus, question types, and scoring of the ACT Math, check out our About ACT Math Test page.
Tricks and Strategies to ace this question type
Pre-algebra questions mainly deal with basic math like adding, subtracting, multiplying, and dividing—you know, the simple things! It's all pretty straightforward.
- Assess Your Comfort Level:
Evaluate your familiarity with pre-algebra skills, considering your math proficiency.
- Focus on Understanding:
Prioritize understanding the essence of problems rather than solely reviewing specific pre-algebra skills.
- Recognize ACT Math Patterns:
Develop your ability to recognize patterns in the wording of ACT math questions.
- Effective Problem Solving:
Practice solving ACT problems systematically, circling keywords and phrases while eliminating unnecessary information.
- Gradual Skill Enhancement:
Progress from a deliberate approach to gradually increasing your speed while problem-solving.
- Time Management:
Track your progress by timing yourself, striving to solve each practice question in an average of under one minute per problem for efficient preparation.
Pre-Algebra examples
Nora the polar bear was born in a zoo. The table below shows her weight, in pounds, each month from when she was born (birth) to age 4 months. What is the average rate of change in Nora’s weight, in pounds per month, from birth to age 4 months?
| Age (Months) | Weight (pounds) |
|---|---|
| Birth | 1.6 |
| 1 | 7.0 |
| 2 | 11.0 |
| 3 | 16.2 |
| 4 | 21.6 |
- 4.0
- 5.0
- 5.4
- 5.8
- 11.6
To calculate the average rate of change in Nora’s weight for the first 4 months after birth, divide her change in weight from birth to the 4th month by her change in age.
The change in weight is how much Nora’s weight changed during the 4 months. Subtract her weight at birth (1.6) from her weight after 4 months (21.6) to find the change in weight (20.0).
The change in age is the number of months that have passed. Subtract the month at Nora’s birth (0) from the last given month (4) to find the change in age (4).

Now divide the change in weight by the change in age to calculate the average rate of change.
| Average rate of change | |
|---|---|
| Plug in values | |
| 5.0 | Divide |
The average rate of change in Nora’s weight, in pounds per month, is 5.0.
Note: The average rate of change in weight from birth to 4 months is the slope of the line in the coordinate plane connecting the points (0,1.6) and (4,21.6), where x corresponds to age and y corresponds to weight.
(Choice A) 4.0 may result from mistakenly counting the birth month and dividing the change in Nora’s weight by 5 months (instead of 4).
(Choice C) 5.4 may result from mistakenly dividing the weight after 4 months (21.6) by 4 instead of dividing the change in weight (20.0) by 4. It may also result from assuming that the change in weight in the 1st month (1.6 to 7.0) or the last month (16.2 to 21.6) is the average rate of change.
(Choice D) 5.8 may result from incorrectly calculating the change in weight by adding (instead of subtracting) Nora’s weight after 4 months (21.6) and her weight at birth (1.6).
(Choice E) 11.6 is the average of Nora’s weight after 4 months and her weight at birth, but the question asks for the average rate of change in her weight.
- To find the change in a quantity, subtract the initial amount from the final amount.
change = (final value) − (initial value)
- To find the average rate of change of a quantity y between two values of x, divide the change in y by the change in x.
Ruslan recorded the temperature, in degrees Celsius, at the same time each day for 6 consecutive days. He recorded a temperature of 16°C on the 1st day and a temperature of −2°C on the 6th day. What was the change in the temperature recorded by Ruslan over the course of the 6 days?
- −18°C
- −3°C
- 3°C
- 14°C
- 18°C
To find a change in temperature over a given time interval, subtract the initial recorded temperature from the final recorded temperature.
Temperature change is positive for an increase and negative for a decrease. The temperature decreased from the 1st day to the 6th, so the change must be a negative value. Eliminate Choices C, D, and E.
It is given that the final temperature recorded by Ruslan on the 6th day was −2°C and the initial temperature recorded on the 1st day was 16°C. Plug these values into the equation to find the change in temperature.
Change in temperature
Plug in values
The change in the recorded temperature from the 1st day to the 6th day was −18°C.
(Choice B) −3°C is a result of dividing the change in temperature (−18) by the number of days (6).
(Choice C) 3°C is a result of mistakenly subtracting the final temperature from the initial temperature (16 − (−2)) and then dividing by the number of days (6).
(Choice D) 14°C is the sum of the two given temperatures but the question asks for the change in temperature from the 1st day to 6th day.
(Choice E) 18°C is a result of mistakenly subtracting the final temperature from the initial temperature (16 − (−2)) instead of subtracting the initial temperature from the final temperature (−2 − 16).
To find the change in a quantity, subtract the initial amount from the final amount.
The greatest common factor of 2 whole numbers is 10, and the least common multiple of these same 2 numbers is 150. What are the 2 numbers?
- 5 and 30
- 10 and 15
- 10 and 30
- 30 and 50
- 50 and 100
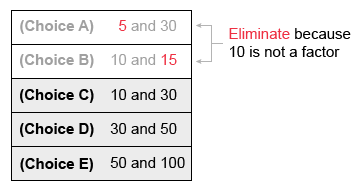
While it is possible to find the greatest common factor (GCF) and the least common multiple (LCM) of each pair of numbers (see alternate method), it is most efficient to answer the question by process of elimination.
It is given that the greatest common factor of the 2 whole numbers is 10, so 10 must be a factor of both whole numbers. Eliminate Choices A and B because each contains a whole number of which 10 is not a factor.
The least common multiple of the 2 whole numbers is given to be 150, so 150 must be the smallest number that is a multiple of both whole numbers.
Notice that 30 is a multiple of 10, (Choice C) and 100 is a multiple of 50 (Choice E). Therefore, the LCM of each pair is the larger number. Eliminate Choices C and E because they do not have an LCM of 150.

By process of elimination, the 2 whole numbers must be 30 and 50.
(Choice A) 5 and 30 have a GCF of 5 (instead of 10) and an LCM of 30 (instead of 150).
(Choice B) 10 and 15 have a GCF of 5 (instead of 10) and an LCM of 30 (instead of 150).
(Choice C) 10 and 30 have a GCF of 10, but they have an LCM of 30 (instead of 150).
(Choice E) 50 and 100 have a GCF of 50 (instead of 10) and an LCM of 100 (instead of 150). These values may result from the misconception that the LCM of two numbers is equivalent to their sum.
Things to remember:
- For a list of numbers:
- The greatest common factor is the largest possible number that divides evenly into each number.
- The least common multiple is the smallest possible number that is a multiple of each number.
- If a question asks for numbers that satisfy given conditions, it may be efficient to reason with the answer choices to answer the question by process of elimination.
Elementary Algebra
In Elementary Algebra1, you'll master the basics of working with equations, solving problems with either numbers and/or expressions, and determining the value of variables. Essential skills in this content area include the ability to simplify algebraic expressions by combining like terms and understanding the relationships between numbers. Additionally, you’ll learn how to convert word problems into simple equations, solving them by isolating the variables.
- The ACT math questions incorporates ten items in elementary algebra, focusing on inequalities, linear equations, ratios, percentages, and averages.
Tricks and Strategies to ace this question type
Algebra expresses equations symbolically using variables like 'a,' 'b,' or 'x.' Unlike regular arithmetic, algebra allows for unknowns in expressions, introducing concepts like "a + b = c." The ACT Math test often includes algebra questions, which test your ability to work with symbolic expressions. Solving algebraic equations, such as "x + 6 = 16," involves finding the numeric value of 'x' that makes the equation true—this value is the solution. The ACT Math test frequently features algebra questions, testing your ability to work with these symbolic expressions.
- Solving Expressions With Substitution
- Master manipulating equations and effectively solving problems with given expressions.
- Develop confidence in substituting numbers as a fundamental skill in algebra.
- Simplifying Algebraic Expressions
- Combine like terms and factorize expressions using basic math properties.
- Apply the associative and distributive properties for practical simplification.
- Writing/Solving Expressions and Equations
- Convert word problems into simple linear equations or expressions for solving.
- Solve equations by isolating the variable on one side and the numbers on the other.
- Multiplying Binomials
- Employ the FOIL method (First, Outer, Inner, Last) when dealing with binomials.
- Recognize the significance of FOIL for efficient multiplication.
- Inequalities
- Treat inequalities like equations, but be mindful of sign changes when multiplying or dividing both sides by a negative number.
- Understand the nuances of inequalities and their solutions for accurate problem-solving.
Elementary Algebra examples
Which of the following polynomials is a factor of x2 + bx − 15, given that x = −3 is a solution to the equation x2 + bx − 15 = 0 ?
- x − 5
- x − 3
- x − 2
- x + 2
- x + 5
A quadratic function with a zero at x = a has the factor (x − a). A zero of a function is a value of x at which the function equals 0.
It is given that x = −3 is a solution to x2 + bx − 15 = 0, so x = −3 is a zero of the quadratic function f(x) = x2 + bx − 15. Plug a = −3 into x − a and simplify to find the corresponding factor.

The factor x + 3 is not a choice, so find the other factor of x2 + bx − 15. The expression x 2 + bx − 15 is in the form x 2 + bx + c and can be factored as (x + m)(x + n), where m and n are integers that multiply to c and add to b.
The value of c is −15 in the given expression and one of the factors is x + 3. Let m = 3.

The value of b is unknown, but 3 and n must multiply to −15. Therefore, n must be −5.
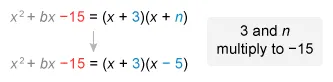
Therefore, the polynomial factors of x2 + bx − 15 are x + 3 and x − 5.
Note: The value of b in the given expression x2 + bx − 15 is not needed to answer the question, but it is possible to determine from the factors x + 3 and x − 5 that b is −2 (the sum of 3 and −5).
(Choice B) x − 3 may result from the misconception that the given solution x = −3 corresponds to a factor of x − 3 (instead of x + 3).
(Choice C) x − 2 may result from a combination of the error described in Choice D and a sign error.
(Choice D) x + 2 may result from mistaking the value of b in the given expression x 2 + bx − 15 to correspond to a factor of the expression.
(Choice E) x + 5 may result from a sign error when determining which integer pair includes 3 and multiplies to −15. It may also result from the error described in Choice B.
Things to remember:
-
A quadratic function with a zero at x = a has the factor (x − a).
-
It may be possible to factor a quadratic expression of the form x 2 + bx + c as (x + m)(x + n), where m and n are integers that multiply to c and add to b.
Given that (x + 4) and (x − 3) are factors of the quadratic expression x2 + ax + a + b, what is the value of b ?
- 13
- 11
- 1
- −11
- −13
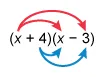
The quadratic expression has two polynomial factors, so the product of the factors must also be a factor of the quadratic expression. Multiply (x + 4) and (x − 3) together to find their product.
|
Product of given factors
|
|
(x)(x) + (x)(−3) + (4)(x) + (4)(−3)
|
Distribute each term in (x + 4) to each term in (x − 3)
|
|
x2 − 3x + 4x − 12
|
Multiply
|
|
x2 + x − 12
|
Combine like terms
|
The expressions x2 + x − 12 and x2 + ax + a + b are simplified and have a matching term (x2), so the given quadratic expression has no other factors and must be equivalent to x2 + x − 12.
If two quadratic expressions are equivalent, then the coefficients of their corresponding terms must be equal. Write x as 1x, and compare the x-term coefficients and the constant terms to create equations for a and b.
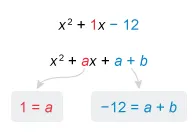
The value of a is 1, so plug a = 1 into −12 = a + b and solve for b.
| −12 = a + b | Constant terms are equal |
| −12 = 1 + b | Plug in a = 1 |
| −13 = b | Subtract 1 from both sides |
The value of b is −13.
(Choice A) 13 may result from the combination of errors described in Choices B and D.
(Choice B) 11 may result from correctly finding that a = 1 but mistakenly solving the equation 12 = a + b (instead of −12 = a + b).
(Choice C) 1 is the value of a, but the question asks for the value of b.
(Choice D) −11 may result from mistaking the value of a to be −1 (instead of 1).
Things to remember:
- If a quadratic expression has two polynomial factors, then the product of the factors must also be a factor of the quadratic expression.
- If two quadratic expressions are equal, then the coefficients of their corresponding terms must be equal.
One of the following quadratic equations has the complex number as a solution. Which one?
- x2 + 3 = 0
- x2 − 3x + 3 = 0
- x2 + 3x + 3 = 0
- x2 − 6x + 12 = 0
- x2 + 6x − 12 = 0
To find a quadratic equation given the complex solution , it is efficient to isolate the radical term in the solution and square both sides of the resulting equation to eliminate the radical.
|
Subtract 3 from both sides to isolate the radical term
|
|
|
Square both sides to eliminate the radical:
|
Notice that each answer choice is an equation in standard form ax2 + bx + c = 0. Expand the perfect square (x − 3)2 on the left side of the equation above and then add 3 to both sides to get an equation in standard form.
|
Expand the perfect square::
(x−3)2=x2−2(x)(3)+32
|
|
|
x2−6x+12=0
|
Add 3 to both sides
|
The equation matches Choice D, so the equation that has as a solution is x2 − 6x + 12 = 0. If the resulting equation did not match a choice, it would be necessary to multiply by a constant to get an equivalent equation.
Note: It is possible to plug into x2 − 6x + 12 = 0 or use the quadratic formula to see that is a solution to x2 − 6x + 12 = 0.
(Choice A) x2 + 3 = 0 is incorrect because the complex number does not satisfy x2 + 3 = 0. It is possible to subtract 3 and take the square root of both sides to solve the equation directly for x or to use the quadratic formula to see that the solutions to this equation are and .
(Choice B) x2 − 3x + 3 = 0 is incorrect because the complex number does not satisfy x2 − 3x + 3 = 0. It is possible to use the quadratic formula to see that the solutions to this equation are and .
(Choice C) x2 + 3x + 3 = 0 is incorrect because the complex number does not satisfy x2 + 3x + 3 = 0. It is possible to use the quadratic formula to see that the solutions to this equation are and .
(Choice E) x2 + 6x − 12 = 0 is incorrect because the complex number does not satisfy x2 + 6x − 12 = 0. It is possible to use the quadratic formula to see that the solutions to this equation are and
Things to remember:
- To find a quadratic equation given a complex solution of the form isolate the radical term in the solution and square both sides of the resulting equation to eliminate the radical.
- The standard form of a quadratic equation is y = ax2 + bx + c, where c is the value of the y-intercept.
Intermediate Algebra
Intermediate Algebra delves into quadratic equations, like, x² – 5x + 6. Learning to factor involves setting up parentheses based on coefficients. The roots, or solutions, are determined by finding the numbers that add to the middle term and multiply by the third term. This foundational skill prepares you for more intricate algebraic problem-solving in the Intermediate Algebra section.
- The ACT Math problems features nine intermediate algebra questions that revolve around exponents, roots, simultaneous equations, and quadratic equations.
Tricks and Strategies to ace this question type
- Mastering Quadratic Equations
- Understand the standard form ax² + bx + c.
- Effectively factorize examples like x² – 5x + 6.
- Apply rules for adding, multiplying, and determining roots.
- Tackling Systems of Equations
- Follow the "n equations with n variables rule" for multi-variable equations.
- Apply substitution and combination methods for efficient problem-solving.
- Unlocking Functions
- Visualize (x, f(x)) as (x, y) and use “pick numbers” for problem-solving.
- Apply “pick numbers” to analyze and compare given functions.
- Demystifying Logarithms
- Recognize logarithms as an exponent alternative.
- Grasp the core concept: logx(y) = a, and refer to a comprehensive list of logarithm rules if needed.
Intermediate Algebra Examples
The function f that is defined as f(x) = 7 − 5x has domain {−1, 0, 3}. What is the range of f ?
- {−8, 2, 12}
- {−8, 7, 12}
- {−2, 0, 6}
- {2, 7, 12}
- {2, 7, 22}
The function notation f(x) represents the output of the function f when the input is x.
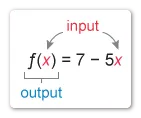
The domain of a function is the set of inputs x at which the function is defined.
The range of a function is the set of outputs f(x) that each correspond to one input in the domain x.
The domain is given to be {−1, 0, 3}. Plug each value from the domain (inputs) into the given function f(x) = 7 − 5x for x to find the range (outputs).
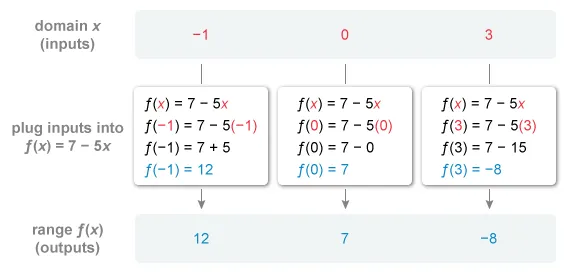
The values in the range of the given function are 12, 7, and −8. To match the order in the choices, arrange the values from least to greatest.
The range of the given function is {−8, 7, 12}.
(Choice A) {−8, 2, 12} is incorrect because 2 is not in the range of the given function. This choice may result from the misconception that plugging 0 into f(x) = 7 − 5x results in 7 − 5 (instead of 7 − 0).
(Choice C) {−2, 0, 6} may result from mistakenly first subtracting and then multiplying when calculating each range value for the given function f(x) = 7 − 5x. However, it is necessary to first multiply and then subtract.
(Choice D) {2, 7, 12} is incorrect because 2 is not in the range of the given function. This choice may result from mistakenly plugging 1 (instead of −1) into f(x) = 7 − 5x or from a sign error when calculating 7 − 5(−1).
(Choice E) {2, 7, 22} may result from mistakenly plugging each input into 7 + 5x instead of into the given function f(x) = 7 − 5x.
Things to remember:
- The domain of a function is the set of x-values at which the function is defined.
- The range of a function is the set of outputs (f(x)) that each correspond to one input in the domain (x).
Which of the following expressions is equivalent to for all nonzero values of x and y ?
The given expression is a rational expression of powers. Simplify the given expression to identify an equivalent expression.
To simplify , divide the constants (−36 and 9) and use the quotient rule to divide powers of x and y.
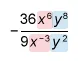 |
Given expression
|
|
|
Divide constants and use the quotient rule:
|
|
|
Simplify
|
The given expression is equivalent to −4x9y6.
Note: The question states “x and y are nonzero” to indicate that the expression is not undefined.
(Choice A) −4x−2y4 may result from mistakenly dividing (instead of subtracting) the exponents.
(Choice B) −4x3y10 may result from mistakenly adding (instead of subtracting) the exponents.
(Choice D) −27x3y10 may result from a combination of the errors described in Choices B and E.
(Choice E) −27x9y6 may result from mistakenly subtracting (instead of dividing) the constants.
Things to remember:
To divide two powers of the same base, use the quotient rule: .
Rodney rides a skateboard at a constant rate along a straight line past his friends Alana, Bucky, Chad, Daewon, and Elissa. His friends record the time t, in seconds, that it takes Rodney to reach them and the distance d, in feet, he is from a reference point. The results are shown in the table below.
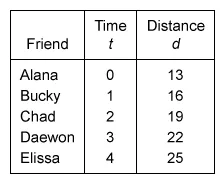
If Rodney is a distance of d = 13 feet from his reference point at time t = 0, which of the equations below represents the relationship between d and t ?
- d = t + 13
- d = t + 16
- d = 3t + 10
- d = 3t + 13
- d = 13t + 3
The distance an object travels at a constant rate can be modeled by a linear equation. The distance d is equal to the product of the rate of change and time plus the initial distance of the object.
distance = (rate)(time) + (initial distance)
It is given that Rodney moves at a constant rate, so use the table to identify the initial distance and to calculate the rate at which the distance d increases with time t.
The initial distance is the distance Rodney is from the reference point at time t = 0. Identify in the given table that the distance d is equal to 13 at time t = 0.

It is possible to eliminate Choices B, C, and E because they do not have an initial distance of 13.
The rate of change is the change in the distance d for each 1-second change in the time t. The rate of change is constant, so find the change in distance between any pair of consecutive times.

For each 1-second increase, the distance increases by 3. It is possible to eliminate Choices A, B, and E because they do not have a rate of change of 3.
Therefore, the equation that represents the relationship between d and t is d = 3t + 13.
(Choice A) d = t + 13 may result from miscalculating the rate of change as 1 (instead of 3).
(Choice B) d = t + 16 may result from miscalculating the rate of change as 1 (instead of 3) and incorrectly identifying the initial distance as the value of d corresponding to time t = 1 (instead of t = 0).
(Choice C) d = 3t + 10 may result from miscalculating the initial distance by subtracting the rate of change (3) from the value of d at t = 0 (13).
(Choice E) d = 13t + 3 may result from mistakenly switching the rate of change and the initial distance.
Things to remember:
- If a quantity y changes at a constant rate with respect to another quantity x, then y is defined by the linear equation:
y = (rate of change)(x) + (initial value of y)
- A constant rate of change in a variable y defined in terms of another variable x is the change in y for each increase of 1 in x.
- An initial value of a variable y defined in terms of another variable x is the value of y when x = 0.
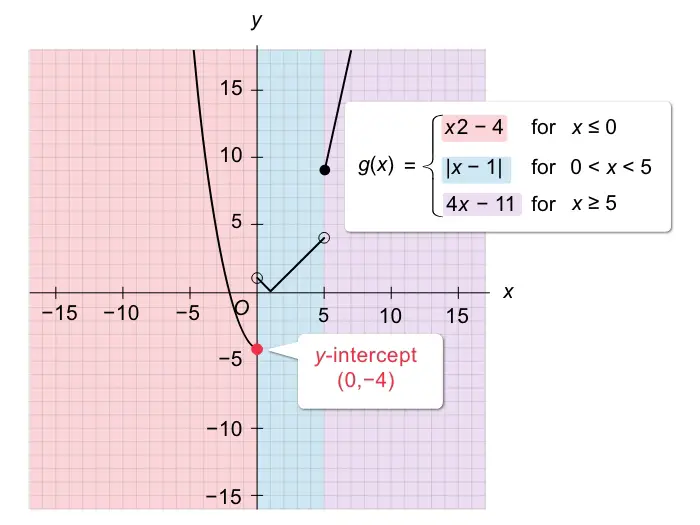
Coordinate Geometry
Coordinate geometry requires a thorough understanding of its various aspects to navigate the diverse questions on the test. Fortunately, once you grasp the fundamentals, coordinate geometry becomes easy to visualize and comprehend. Coordinate geometry involves working with line graphs on the (x, y) coordinate plane.
- ACT Math question types include nine coordinate geometry problems that focus on slope, distance, midpoint, parallel and perpendicular lines, points of intersection, and graphing.
Tricks and Strategies to ace this question type
Coordinate plane questions assess your comprehension of its mechanics, focusing on how to manipulate points and lines. These questions may test your understanding of the coordinate plane’s infinite expanse, your grasp of negative and positive x and y coordinate values, and your ability to visualize the movement of points across the coordinate plane.
- Note Down Given Information
- Resist the temptation to solve coordinate geometry problems mentally.
- Avoid mistakes by writing down given information, especially with negatives or absolute values.
- When a diagram lacks coordinates, jot down the information to organize your thoughts.
- Visualize with Drawings
- Sketch scenarios, even creating your own diagrams when none are provided.
- Mark details on sketches to help manage information effectively.
- Invest a small amount of time in drawing, saving energy and preventing mental overload.
- Select Formulas Wisely
- Decide which formulas to use beforehand, preventing last-minute confusion.
- If comfortable, memorize additional formulas, but ensure accuracy through practice.
- Focus on key formulas, such as the Pythagorean theorem, and prioritize quality over quantity.
Coordinate Geometry Examples
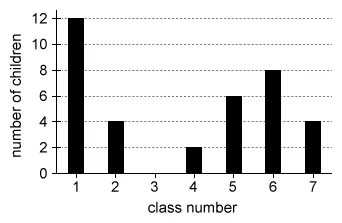
The bar graph below shows the number of children enrolled in the after-school program from the 7 classes at Sunshine Children’s Learning Center. What is the probability that a child selected at random from the after-school program is from Class 2 ?
To find the probability of a desired event, use the following formula:

The number of desired outcomes is the number of children enrolled from Class
2.
The number of
possible outcomes is the total number of children enrolled in the after-school
program.

The horizontal axis represents Classes 1 through 7, and the vertical axis represents the number of children enrolled. Therefore, the height of each bar represents the number of children from the corresponding class.
Use the given bar graph to identify the number of children from Class 2 and the total number of children enrolled in the after-school program.
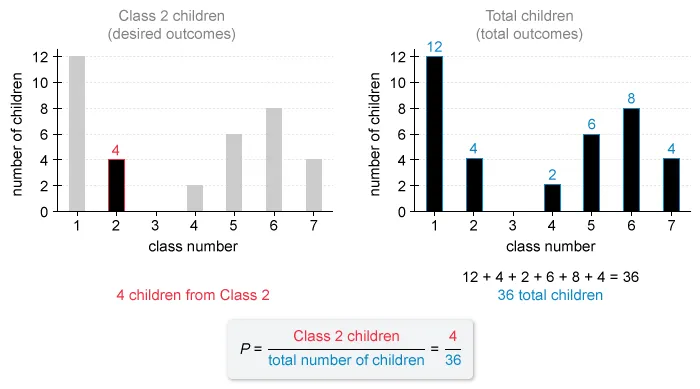
To match the choices, simplify to see that the probability that a child selected at random from the after-school program is from Class 2 is .
(Choice A) may result from the misconception that the number of desired outcomes is 1 because a single child was selected, or because the child was selected from a single class.
(Choice B) may result from the misconception that the number of desired outcomes is equal to the class number (instead of the number of children in Class 2).
(Choice D) is the probability that Class 2 was selected from the total number of classes (instead of the probability that a child from Class 2 was selected from the total number of children).
(Choice E) may result from the misconception that the total number of possible outcomes is the total number of classes (instead of the total number of children).
Things to remember:
- To find the probability of a desired event, use the following formula:
- On a bar graph, the height of each bar defined on the horizontal axis corresponds to the value given on the vertical axis.
Which of the following is an equation of a parabola that passes through the points labeled in the standard (x,y) coordinate plane below?
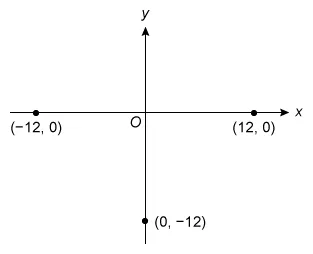
It is given that the graph is a parabola, so the equation must be a quadratic equation. A quadratic equation is a polynomial that can have at most 2 polynomial factors.
Any equation with more than 2 polynomial factors is not quadratic, so eliminate Choices C, D, and E because they are not quadratic equations.

The remaining choices are quadratic equations in factored form y = a(x − p)(x − q), where p and q are the x-intercepts and a is the scale factor that determines the opening direction of the parabola.
The parabola opens upward if the value of a is positive and downward if the value of a is negative.

Notice that the graph of the parabola through the 3 given points opens upward.
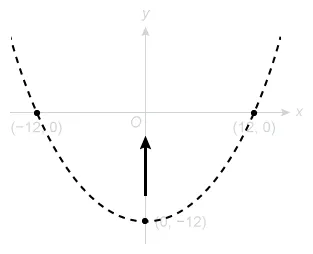
Therefore, the equation of the parabola in factored form must have a positive value of a. Eliminate Choice B because the value of a is negative

By process of elimination, an equation of the parabola is
(Choice B) may result from not considering the opening direction of the parabola.
(Choices C, D, and E) These equations are incorrect because the equation of a parabola has at most two polynomial factors. They may result from the misconception that the factored form of a quadratic equation displays the x– and y-intercepts as constants, but the y-intercept appears as a constant only in the standard form of the equation.
Things to remember:
The factored form of a quadratic function is f(x) =
a(x − p)(x − q), where p and q are the
x-intercepts of the parabola and a is the scale factor that determines the opening
direction.
- If the scale factor a is positive, the graph is an upward-opening parabola.
- If the scale factor a is negative, the graph is a downward-opening parabola.
In the standard (x,y) coordinate plane, the graph of has a vertical asymptote at:
- x = 2
- x = 3
- x = 5
- x = 10
- x = 30
A vertical asymptote is a vertical line that a graph approaches but never intersects. As a graph approaches a vertical asymptote, the y-values of the graph go to positive or negative infinity.
For the graph of a rational equation, a vertical asymptote can exist only at a value of x where a rational expression is undefined. A rational expression is undefined at any value of x where the denominator is equal to 0.

The denominator is 5x − 10, so set this expression equal to 0 and solve for x to find where the rational expression is undefined.
| 5x − 10 = 0 | Set the denominator equal to 0 |
| 5x = 10 | Add 10 to both sides |
| x = 2 | Divide both sides by 5 |
The rational expression in the given equation is undefined only when x = 2.
Therefore, the graph of must have a vertical asymptote at x = 2.
Note: A vertical asymptote exists only when the numerator is not also equal to 0. When the denominator and numerator are both 0, there is a hole in the graph. Plug x = 2 into the equation to verify it is a vertical asymptote.
(Choice B) x = 3 is the ratio of the constant terms in The ratio of constant terms corresponds to the y-intercept of the graph but the question asks for the vertical asymptote.
(Choice C) x = 5 may result from mistakenly setting the numerator 6x − 30 (instead of the denominator 5x − 10) equal to 0, but this corresponds to an x-intercept of the graph (instead of a vertical asymptote).
(Choices D and E) x = 10 and x = 30 may result from mistaking a constant term in the given rational equation to be the location of the vertical asymptote of the graph. However, the given function is defined at x = 10 and x = 30.
Things to remember:
The graph of a rational equation has a vertical asymptote at any value of x where the denominator is equal to 0 and the numerator is not equal to 0.
Plane Geometry
Although you might manage the ACT without a strong grasp of trigonometry or intermediate algebra, a solid understanding of plane geometry is indispensable. This is crucial as geometry questions make up a substantial portion of the test.
- The ACT Math questions features 14 plane geometry items based on angles, lengths, triangles, quadrilaterals, circles, perimeter, area, and volume.
Tricks and Strategies to ace this question type
Plane geometry problems rank among the most challenging questions on the ACT math section, typically requiring more time and completion in multiple steps. Use this awareness to prioritize your study efforts in the most productive areas.
- Clarify the Problem
- Identify the specific information the problem seeks for solids like cubes or spheres.
- Understand whether you're asked to find volume, surface area, or both.
- Recognize the relevant formulas and elements of the geometric solid(s) involved.
- Visualize with Drawings
- Draw a sketch when the problem describes a solid without a provided image.
- Improve your understanding by visualizing the information and its application to the question.
- Apply Formulas Efficiently
- Apply the identified formulas by plugging in the provided information.
- If formulas escape memory, resort to alternative methods like the Pythagorean theorem.
- Ensure Clarity and Accuracy
- Label your work meticulously to avoid falling into trap answers.
- Double-check your solution for consistency and correctness, especially in a high-stress setting.
Plane Geometry Examples
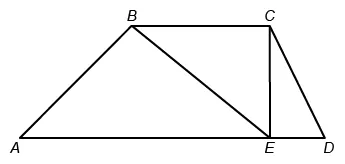
In the figure below, ABCD is a trapezoid with perpendicular to is 8 inches long; and is 22 inches long. If the area of right triangle △BCE is 40 square inches, what is the area, in square inches, of trapezoid ABCD?
- 88
- 108
- 120
- 128
- 150
The formula for the area of a trapezoid is , where b1 and b2 are the lengths of the parallel bases and h is the height of the trapezoid (distance between the bases).
The bases of given trapezoid ABCD are and and the height is . Label the figure with the given information CE = 8 inches, AD = 22 inches, and the area of right triangle △BCE = 40 square inches.
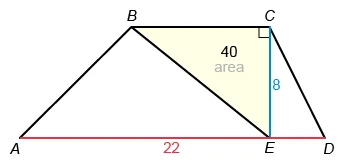
To find the area of ABCD, first find the base BC. Notice that is also the base of triangle △BCE. Use the given area of triangle △BCE and height CE = 8 to find the unknown length BC.
The formula for the area of a triangle is , where b is the length of the base and h is the height. Plug in A = 40 and h = 8, and solve for b (the length of ).
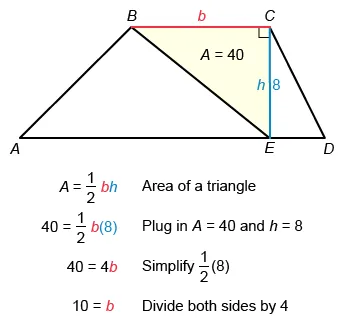
Therefore, base BC = 10. The base AD = 22 and height CE = 8 are given for trapezoid ABCD, so plug b 1 = 10, b 2 = 22 and h = 8 into the formula for the area of a trapezoid and simplify.
Note: It does not matter which base is chosen as b1 and which is chosen as b2.
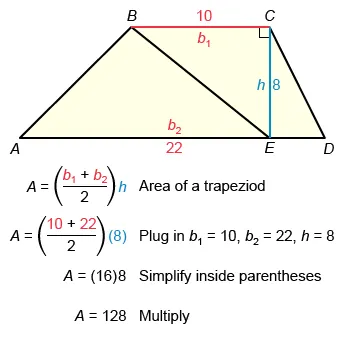
The area of trapezoid ABCD is 128 square inches.
(Choice A) 88 may result from mistakenly plugging the given lengths 8 and 22 into the formula for the area of a triangle .
(Choice B) 108 may result from using the incorrect formula (instead of ) when calculating BC.
(Choice C) 120 may result from the misconception that the area of trapezoid ABCD is 3 times the area of triangle BCE.
(Choice E) 150 may result from mistakenly switching the height 8 and the base of length 10 when calculating the area of the trapezoid.
Things to remember:
- The formula for the area of a trapezoid is , where b1 and b2 are the lengths of the bases (parallel sides) and h is the height(perpendicular distance between the bases).
- The formula for the area of a triangle is , where b is the length of the base and h is the height.
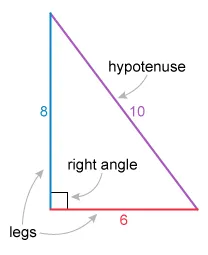
What is the area, in square centimeters, of a right triangle with side lengths of 6 cm, 10 cm, and 8 cm ?
- 24
- 30
- 40
- 48
- 60
A right triangle is formed by 2 perpendicular legs and a hypotenuse. The hypotenuse is the longest side, and it is located opposite the right angle. The legs are the shorter sides that form the right angle.
The longest given side length is 10 cm, and the shorter lengths are 6 cm and 8 cm. Draw a right triangle with perpendicular legs of lengths 6 and 8 and a hypotenuse of length 10 opposite the right angle.
The formula for the area of a triangle is is where b is the length of the base and h is the height. The height is the perpendicular distance from the base to the vertex opposite the base.
Therefore, the base and height of a right triangle are the legs. Let one leg be the base and the other leg be the height, and plug their lengths (6 and 8) into the formula for b and h to find the area of the right triangle.
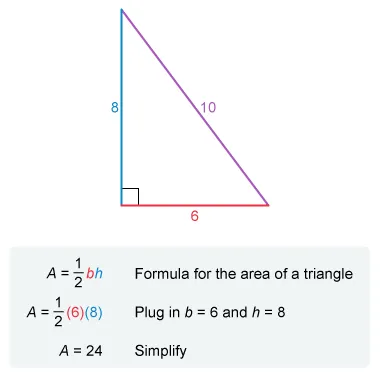
The area of the right triangle, in square centimeters, is 24.
Note: It does not matter which leg is assigned to be the base and which is assigned to be the height.
(Choices B and C) 30 and 40 may result from misidentifying 10 (the greatest given length) as the base or height of the triangle. However, the longest side of a right triangle is the hypotenuse, and the base and height of a right triangle are the legs.
(Choice D) 48 may result from using the incorrect formula but the formula for the area of a triangle is
(Choice E) 60 may result from plugging the lengths of the hypotenuse (10) and the shorter leg (6) into the incorrect formula
Things to remember:
- The formula for the area of a triangle is , where b is the length of the base and h is the height.
- In a right triangle, the legs are the base and the height.
In the circle below, radius and radius each have a length of 6 inches, and the measure of is 170°. The shaded sector is bounded by these radii and minor arc What is the area, in square inches, of the shaded sector of the circle?
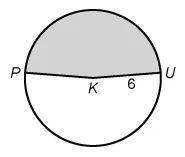
Ratios of the part to the whole are equivalent between the area of a circular sector and the measure of its intercepting central angle.
The area of the shaded sector (part) divided by the area of the entire circle (whole) must equal the measure of its intercepting central angle (part) divided by the measure of the entire circle (whole), forming the following proportion:
The formula for the area of a circle is (proof), where r is the length of the radius. The given measure is in degrees, so use 360° for the measure of a whole circle (instead of 2π radians).
Now plug in the given central angle measure (170°) and radius (6) , and then solve for the desired area of the shaded sector.
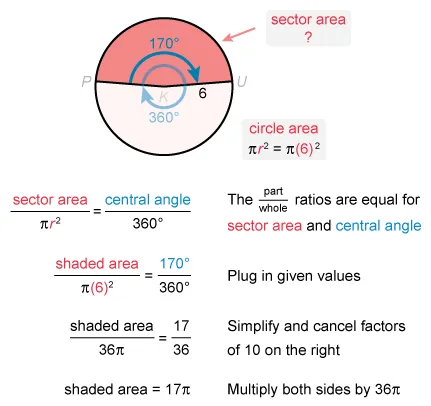
The area, in square inches, of the shaded sector of the circle is .
(Choice A) is approximately the length of minor arc but the question asks for the area of the shaded sector.
(Choice B) is the circumference of the circle, but the question asks for the area of the shaded sector.
(Choice D) is the area of the unshaded sector, but the question asks for the area of the shaded sector.
(Choice E) is the area of the entire circle, but the question asks for the area of only the shaded sector.
Things to remember:
- Ratios of the part to the whole are equivalent between the area of a circular sector and the measure of its intercepting central angle. The following proportion relates circular sectors and central angles of a circle:
- The formula for the area of a circle is , where r is the length of the radius.
Trigonometry
Trigonometry studies the relationships between the sides and angles of right triangles. The ratios between the measures of the sides of a right triangle and the measures of its angles are consistent, no matter how large or small the triangle.
- ACT Math problems includes four questions based on basic sine, cosine, tangent functions, trig identities, and graphing.
Tricks and Strategies to ace this question type
- Understand Basic Trigonometric Concepts
- Master fundamental concepts such as sine, cosine, tangent, and reciprocal functions.
- Familiarize Yourself with Trigonometric Identities
- Grasp essential trigonometric identities to simplify expressions and solve problems efficiently.
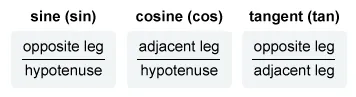
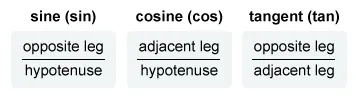
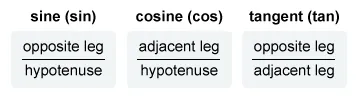
- Recall the SOHCAHTOA acronym
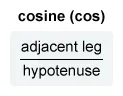
- Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
- Right Triangle Trigonometry
- Apply trigonometric principles to right-angled triangles for problem-solving.
- Recognize the relationships between angles and sides in a right triangle.
- Practice Problem-Solving
- Regularly practice solving diverse trigonometry problems to enhance proficiency.
- Review Special Trigonometric Values
- Memorize special values for common angles for quick calculations.
- Manage Time Effectively
- Develop time-management skills to allocate appropriate time to each trigonometry question.
- Utilize Calculator Functions Wisely
- Leverage calculator2 functions effectively, but ensure a solid understanding of concepts without over-reliance.
- Stay Calm and Focused
- Maintain composure during the test and stay focused on applying trigonometric concepts strategically.
- Review Mistakes for Improvement
- Improve your trigonometry skills continuously by learning from mistakes made on practice tests.
Trigonometry examples
A mail sorting facility uses a conveyor belt to move boxes. An inclined section of the conveyor moves boxes from a horizontal belt upward to another horizontal belt 15 feet higher, as shown below. The inclined section is 39 feet long and covers a horizontal distance of 36 feet. Which of the following expressions gives the measure of the angle between the inclined section of the conveyor and the horizontal?
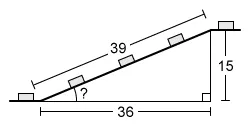
To find the unknown measure of an angle in a right triangle from its trigonometric ratio (sin, cos, tan) , use the corresponding inverse trigonometric function .
Notice that all answer choices contain the inverse cosine function, so let the unknown measure of the angle between the inclined section and the horizontal be θ and first find the cosine ratio:
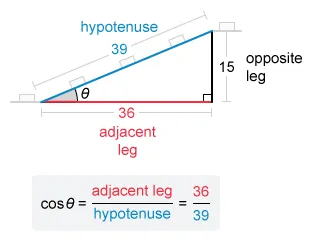
The cosine ratio of θ is equal to
Note: The answer choices contain 36 and 39, so do not reduce this fraction.
The inverse cosine function takes the value of a cosine ratio of an angle as the input, and outputs the measure of the angle. Therefore, take the inverse cosine of to find the measure θ of the angle.

The measure of the angle between the inclined section and the horizontal is see measure on figure.
Note: algebraic way to solve for θ is to take the inverse cosine of both sides of
(Choice A) may result from mistakenly using the ratio instead of to identify the cosine ratio of the angle.
(Choice B) may result from mistakenly using the ratio instead of to identify the cosine ratio of the angle.
(Choice D) may result from mistakenly using the ratio instead of to identify the cosine ratio of the angle.
(Choice E) may result from mistakenly using the ratio instead of to identify the cosine ratio of the angle.
Things to remember:
- Use inverse trigonometric functions to find the measure of an unknown angle from its corresponding ratio
- An inverse trigonometric function takes the value of a trigonometric ratio of an angle as the input, and
outputs the measure of the angle. For example:
In the right scalene triangle shown below, one angle measure and 2 side lengths, in meters, are given. In terms of a and b, what is cos θ?
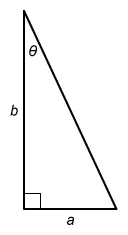
The cosine of an acute angle in a right triangle is equal to the following ratio of side lengths:
In the given right triangle, the leg with length a is opposite angle θ and the leg with length b is adjacent to angle θ.
The length of the hypotenuse is not given, so use the given side lengths and the Pythagorean theorem to find the hypotenuse in terms of a and b.

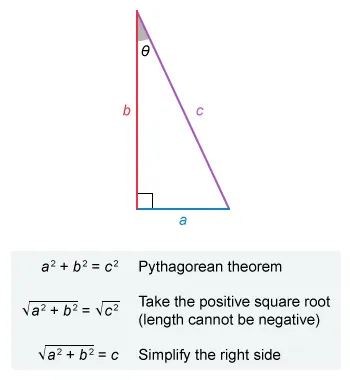
The Pythagorean theorem states that a 2 + b 2 = c 2, where a and b are the lengths of the legs of a right triangle with a hypotenuse of length c.
Let the hypotenuse of the given triangle be c, and solve for c in terms of a and b.
The length of the hypotenuse is Now use the cosine ratio to find which expression is equal to cos θ.
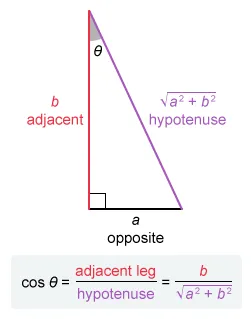
In terms of a and b, .
Note: The question states that the given triangle is scalene, so a and b are not equal. If a was equal to b, then Choices C and D would be equivalent.
(Choice A) is the tangent ratio of θ , but the question asks for the cosine ratio .
(Choice B) may result from mistaking the cosine ratio to be , instead of
(Choice C) is the sine ratio of θ , but the question asks for the cosine ratio .
(Choice E) may result from mistaking the cosine ratio to be , instead of
Things to remember:
- Three main trigonometric ratios are defined for an acute angle in a right triangle: sine,
cosine, and tangent. Each is equal to a specific ratio of side lengths:
- The Pythagorean theorem states that a 2 + b 2 = c 2, where a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse.
A vertical flagpole has a 25-foot wire attached as shown in the figure below. The wire forms an angle of 47° with the level ground. The distance along the pole, in feet, between the ground and the top of the wire is equal to which of the following expressions?
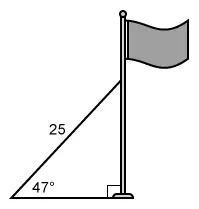
The wire, flagpole, and level ground form a right triangle. Only one of the side lengths of the triangle is given, so it is necessary to use a trigonometric ratio to find the distance between the ground and the top of the wire.
Three main trigonometric ratios are defined for an acute angle in a right triangle: sine, cosine, and tangent. Each equals a specific ratio of side lengths.
The given figure shows the length of the hypotenuse (25) and a 47° angle. Notice that the side that represents the desired distance is opposite the 47° angle. Let this desired distance be x.
The sine ratio relates the opposite leg and the hypotenuse, so use this ratio to write an equation in terms of the unknown distance x.
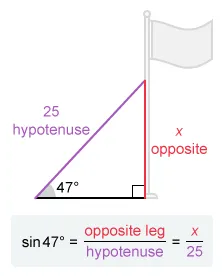
Therefore, Isolate x to find the desired distance.
Multiply both sides by 25 to isolate x
The distance along the pole, in feet, between the ground and the top of the wire is equal to the expression .
(Choice A and B) and may result from the misconception that the sides are related by the ratios of side lengths in a 30-60-90 special right triangle.. The given angle is 47°, so it is not a special right triangle and it is necessary to use trigonometric ratios to find the desired distance.
(Choice D) 25 cos 47° may result from mistakenly using the cosine ratio instead of the sine ratio .
(Choice E) may result from mistaking the side with length 25 to be adjacent to the 47° angle (instead of the hypotenuse).
Things to remember:
Three main trigonometric ratios are defined for an acute angle in a right triangle: sine, cosine, and tangent. Each equals a specific ratio of side lengths.
Additional Topics in Math
The ACT Math test covers a broad range of topics, including additional math concepts that go beyond the traditional high school curriculum. Within the test, you'll encounter various ACT Math question types designed to assess your proficiency in different areas of mathematics.
- Complex Numbers:
- Work with complex numbers, understanding their properties and operations.
- Matrices and Vectors:
- Apply matrix and vector operations, including addition, multiplication, and transformations.
- Logarithmic and Exponential Functions:
- Review logarithmic and exponential functions, along with their applications.
- Conic Sections:
- Understand conic sections, including circles, ellipses, hyperbolas, and parabolas.
- Sequences and Series:
- Analyze sequences and series, recognizing patterns and calculating sums.
- Probability and Statistics:
- Apply advanced probability and statistics concepts, including conditional probability and statistical inference.
- Fundamental Calculus Concepts:
- Grasp fundamental calculus concepts without digging into extensive topics.
Additional topics in Math examples
The 1st term in the geometric sequence below is 4. If it can be determined, what is the 5th term?
4, −12, 36,−108, ⋯
- −324
- −144
- 144
- 324
- Cannot be determined from the given information
A geometric sequence is a sequence of numbers where each term after the first is equal to the previous term multiplied by a fixed number called the common ratio.
To find the common ratio, divide any term after the first by the previous term. Divide the 2nd term (−12) by the 1st term (4) to calculate the common ratio of the given sequence.
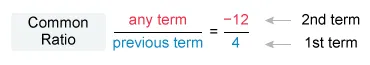
The common ratio simplifies to −3. Therefore, each term of the sequence is equal to the previous term multiplied by −3.
The given sequence has four terms, so the 5th term is the next term in the sequence. To find the next term, multiply the last given term (−108) by −3.
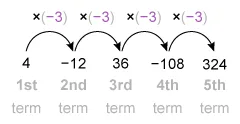
The 5th term of the geometric sequence is 324.
Elimination strategy
Consecutive terms in the given sequence are opposite in sign, so the geometric sequence must have a negative common ratio. Therefore, the sign alternates with each successive term.
In the given sequence, the 1st term is positive (4). All terms in odd positions (1st term, 3rd term, …) are positive, and all terms in even positions (2nd term, 4th term, …) are negative.

The question asks for the 5th term (an odd position), so the desired term must be positive. It is therefore possible to eliminate Choices A and B because they are negative.
(Choice A) −324 may result from a sign error when finding the 5th term.
(Choice B) −144 may result from mistakenly subtracting the 3rd term (36) from the 4th term (−108). However, to calculate the next term in a geometric sequence, it is necessary to multiply the last given term (−108) by the common ratio (−3).
(Choice C) 144 may result from a combination of the errors described in Choices A and B.
(Choice E) “Cannot be determined from the information given” may result from the misconception that it is necessary to be given the common ratio to find the 5th term, but the common ratio can be determined from any two consecutive terms of a geometric sequence.
Things to remember:
- In a geometric sequence, each term after the first is equal to the previous term multiplied by a common ratio.
- To find the common ratio of a geometric sequence, divide any term by the previous term.
Max is playing a game involving 3 fair 6-sided cubes with the digits 1 through 6 on its faces, 1 digit per face. He will roll 3 cubes at the same time and will be awarded 4 points for each cube that has an odd number on its top face. Let the random variable X represent the total number of points awarded on any 1 roll. What is the expected value of X ?
- 2
- 6
- 12
- 24
- 36
The expected value (EV) of a random variable is the expected average value of doing an action a large number of times.
The expected value of multiple events (all 3 cube rolls) is equal to the sum of the expected values of all events (all cube rolls).
To find the expected value of a single event, multiply the value of a success by the probability of that success. Each of the 3 cube rolls has the same value and probability of success.
The value of a success is the value of landing on an odd number (given to be 4 points), and the probability of that success is the probability that the cube will land with an odd number face up (equal to ).
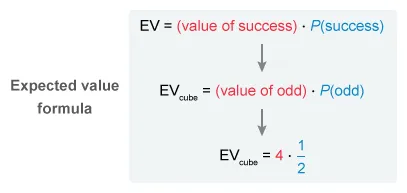
Multiply to see that the expected value of a single cube is 2 points.
The expected value of each cube is the same because the value of each odd number (1, 3, 5) is not related to the points awarded. Multiply the expected value for a single cube (2 points) by the number of cubes (3).

The expected value of Max rolling 3 cubes is 6 points.
Note: The expected value may not be a possible value for a single attempt because it is the expected average of a large number of attempts. The EV is 6 points even though it is not a possible value for a single roll of the cubes.
(Choice A) 2 is the expected value of rolling a single cube, but the question asks for the expected value of rolling all 3 cubes.
(Choice C) 12 is the maximum number of points that Max can receive, but the question asks for the expected value of the 3 cube rolls.
(Choice D) 24 may result from the error described in Choice C and the misconception that points are awarded for any number (1 through 6), but it is given that points are awarded only for odd numbers (1, 3, 5).
(Choice E) 36 may result from the misconception that the expected value of a single cube roll is the number of points awarded for an odd number multiplied by the average of the odd numbers (instead of the probability that the number is odd).
Things to remember:
-
The expected value of a random variable is the expected average value of attempting an action many times. However, it may not be possible to achieve that value on a single attempt.
-
The expected value of multiple events is equal to the sum of the expected values of all events.
-
To find the expected value of a single event, multiply the value of a success by the probability of that success.
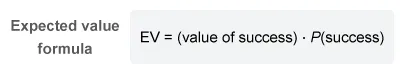
One of the following matrices is equal to the matrix product . Which one?
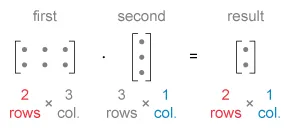
In a defined matrix product, the resulting matrix always has the same number of rows as the first matrix and the same number of columns as the second matrix.
In the given matrix product, the first matrix is a 2 × 2 matrix (2 rows, 2 columns) and the second is a 2 × 1 matrix (2 rows, 1 column), so the resulting matrix must be a 2 × 1 matrix (2 rows, 1 column).
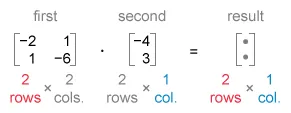
Set up the matrix product and the resulting 2 × 1 matrix.

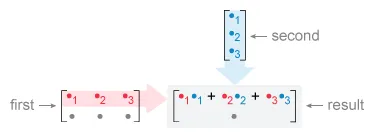
To calculate each entry in a particular row and column of the resulting matrix, pair entries from that row of the first matrix (moving left to right: with entries from that column of the second matrix (moving top to bottom: ).
Find the product of each pair, and then add all the products to find the result.

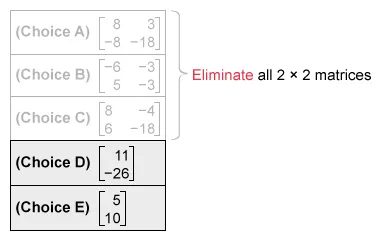
Eliminate choice E because the entry in the first row is not 11.

The given matrix product is equal to the matrix To verify the result, see complete calculation.
Note: In matrix multiplication, the order of the matrices matters. For example, the given product is equal to , but the reordered productis undefined..
(Choices A, B, and C) and cannot be equal to the given matrix product because they are 2 × 2 matrices. The matrices in the given product have dimensions of 2 × 2 and 2 × 1, so the result must be a 2 × 1 matrix.
(Choice E) may result from mistakenly subtracting (instead of adding) when calculating the entries of the resulting matrix.
Things to remember:
- In a matrix product, the resulting matrix must have the same number of rows as the first matrix
and the same number of columns as the second matrix. For example:
- To calculate a matrix product, align the first and second matrices at the left and top edges of
the resulting matrix, respectively. To calculate each entry, use the pattern below to multiply
pairs of entries and add them.
Key Takeaways
Understanding the complexities of ACT Math is like untangling a web of mathematical concepts. Our guide, enriched with sample questions, can help you decode everything from algebraic equations to geometry challenges, providing practical tips and ACT math strategies for every question type. UWorld, a premier test prep resource, gives you access to unlimited exam-level practice, including a comprehensive collection of ACT Math sample questions, to boost your skills. Dive into detailed explanations that shed light on the reasoning behind each answer, helping you understand why certain solutions are correct. With these resources at your fingertips, you'll be well-equipped to tackle the ACT Math section with confidence and precision, setting the stage for a successful test-taking experience.
References
1(2024). Mathematics Test Description for the ACT. Act.org. Retrieved January 5, 2024, from https://www.act.org/content/act/en/products-and-services/the-act/test-preparation/description-of-math-test.html
2(2024). Math Test Tips. Act.org. Retrieved January 5, 2024, from
https://www.act.org/content/act/en/students-and-parents/high-school-success/testing-advice-for-the-act/act-math-test-tips.html