What Is Problem Solving and Data Analysis on the SAT Math?
Problem Solving and Data Analysis on the SAT® Math section focuses on how well students can interpret real-world information and use math to make sense of it. This area tests your ability to work with ratios, percentages, unit rates, and basic statistics using data presented in tables, graphs, and charts. You may be asked to analyze survey results, compare quantities, or draw conclusions from given data sets. Many SAT problem-solving and data analysis questions also involve modeling situations with equations or expressions. Overall, this skill set measures practical math reasoning rather than abstract calculation, making SAT Math problem solving and data analysis especially relevant to everyday scenarios.
SAT Problem Solving & Data Analysis Question Types
SAT Problem Solving and Data Analysis questions are designed to reflect real-life situations where math is used to evaluate information and make decisions. These problems often combine numerical reasoning with data interpretation, requiring students to read carefully and choose the most efficient approach. In this part of the test, accuracy depends as much on understanding the context as it does on performing calculations.
1. Proportion & Percentage Word Problems
These questions test how well you can compare quantities using ratios, fractions, and percentages. You may need to find the percent increase or decrease, calculate discounts, or determine one quantity based on its relationship to another. Many problem-solving and data analysis SAT questions describe everyday situations like test scores, population changes, or pricing.
Things to Remember:
- Always convert percentages to decimals or fractions before setting up equations.
- Identify the base value first, since percent changes depend on the original amount.
- Watch for keywords like increase, decrease, of, and percent more than, which signal different setups.
- In problem solving and data analysis SAT questions, check that your final value makes sense in context.
2. Real-World Rate/Unit Problems
Rate and unit questions focus on relationships such as miles per hour, cost per item, or work completed over time. These SAT Math problem-solving and data analysis problems often require you to set up ratios correctly and pay close attention to units.
Things to Remember:
- Write rates as fractions to keep units visible throughout the problem.
- Make sure all quantities are in the same unit before calculating.
- Look for opportunities to simplify ratios before multiplying or dividing.
- Many SAT Math problem-solving and data analysis errors come from unit mismatches, not incorrect math.
3. Data Interpretation Problems
Data interpretation questions ask you to analyze information presented in tables, charts, or written summaries. You may need to compare values, identify trends, or draw conclusions supported by the data.
Things to Remember:
- Read titles, labels, and footnotes before analyzing the data.
- Base conclusions only on the information shown, not assumptions.
- Compare values carefully rather than relying on visual impressions.
- Strong SAT data analysis practice helps build confidence with tables and charts.
4. Statistics & Probability Problems
These questions cover concepts such as mean, median, range, probability, and simple random sampling. You may also see questions about how changes to a data set affect its average. These problems reward careful reading and organized calculations during SAT problem-solving and data analysis practice.
Things to Remember:
- Know how each measure of center or spread is calculated and what it represents.
- When data changes, consider how the change affects the entire set, not just one value.
- For probability, identify the total number of outcomes before counting favorable ones.
- Organized work is essential during SAT problem-solving and data analysis practice to avoid careless mistakes.
5. Data Table, Graph, & Chart Questions
In these questions, information is displayed visually through bar graphs, line graphs, scatterplots, or two-way tables. You may need to extract specific values, compare categories, or interpret what the visual representation shows overall. Practicing SAT data analysis practice problems helps students avoid common mistakes like misreading axes or labels.
Things to Remember:
- Check axis labels, scales, and units before interpreting any values.
- Do not assume trends beyond the data shown, especially in scatterplots.
- When comparing categories, focus on numerical differences rather than visual height or spacing.
- Regular practice with SAT data analysis practice problems reduces errors caused by misreading graphs or tables.
Students who want structured guidance through these question types often benefit from a focused SAT prep course that includes concept lessons, worked examples, and timed practice aligned with Problem Solving and Data Analysis skills.
Strategies to Solve SAT PSDA Questions Faster & More Accurately
Approaching SAT problem-solving and data analysis questions with a clear plan can save time and reduce mistakes. These problems often look long, but most can be simplified by focusing on the math skills being tested rather than the story around them. The strategies below help students work efficiently while staying accurate across different SAT Math problem-solving and data analysis question types.
- Read for Purpose, Not for Detail: Start by identifying what the question is asking you to find before reviewing all the information. Many problem-solving and data analysis SAT questions include background details that are not directly needed. Focusing on the goal helps you avoid unnecessary calculations.
- Organize Information Before Solving: Write down key numbers, ratios, or relationships in a clear format such as a table or equation. This step is especially helpful for data analysis SAT questions that combine multiple values or conditions. Organized work leads to fewer setup errors.
- Use Estimation to Eliminate Choices: Estimation is a powerful tool when answer choices are far apart. For SAT data analysis problems involving percentages or averages, a quick estimate can often rule out two or three options immediately, saving valuable time.
- Pay Close Attention to Units and Labels: Always check units in word problems, tables, and graphs before solving. Many mistakes in SAT problem solving and data analysis occur when students mix units or misread axis labels. A quick unit check can prevent incorrect answers.
- Check for Reasonableness: After solving, ask whether your answer makes sense in the context of the problem. This habit is crucial during SAT data analysis practice problems, where misinterpreting data can lead to unrealistic results.
- Practice with Real SAT-Style Questions: Speed and accuracy improve with consistent exposure to SAT practice questions. Targeted SAT problem-solving and data analysis practice helps you recognize common structures, apply strategies faster, and stay confident under timed conditions.
SAT Problem Solving & Data Analysis Practice Questions (With Explanations)
Practicing realistic questions is one of the most effective ways to improve performance in SAT problem-solving and data analysis. Working through timed examples helps you apply concepts like ratios, statistics, and data interpretation in test-style scenarios. Reviewing explanations for SAT problem-solving and data analysis practice questions also reinforces efficient setups and common shortcuts.
Question
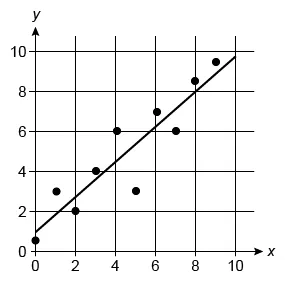
The scatterplot shows the relationship between two variables, x and y. A line of best fit is also shown. For p% of the data points, the line of best fit predicts a y-value less than the actual y-value. What is the value of p ?
Explanation
Correct Answer : 60
To find the value of p, first identify both the total number of data points and the number of data points for which the line of best fit predicts a y-value less than the actual y-value on the given scatterplot.
Count the total number of data points. A line of best fit predicts a y-value less than the actual y-value for any point (x, y) that lies above the line, so count the number of points that lie above the line.
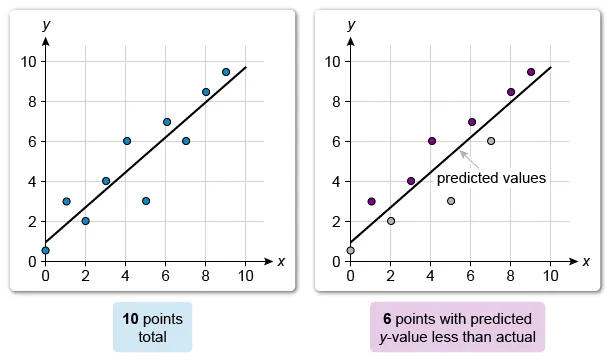
There are 10 total data points and 6 data points that have a predicted y-value that is less than the actual y-value. It is given that the line of best fit predicts a y-value less than the actual y-value for p% of the data points.
A percent of a number is equal to the percent as a fraction multiplied by that number. Rewrite p% as and write an equation.
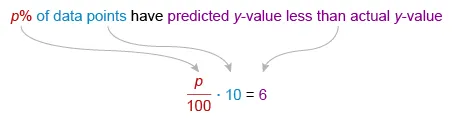
Now solve for p.
| Multiply by 100 on both sides | |
| Divide by 100 on both sides |
The value of p is 60, which means that 60% of the data points have a predicted y-value that is less than the actual y-value.
Things to remember:
- The data points on a scatterplot represent actual values, and a line of best fit predicts a relationship between x and y based on the data points.
- A percent of a number is equal to the percent as a fraction multiplied by that number.
Question
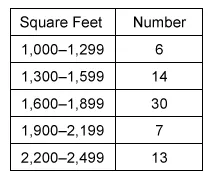
The table above gives the number of homes in a certain neighborhood that have an amount of square feet within the interval listed. Of the homes that have at least 1,600 square feet, what fraction have at least 1,900 square feet?
Explanation
Correct Answer: 2/5
To find the desired fraction of homes, consider the desired part to the whole.
The whole is the total number of homes that have at least
1,600 square feet.
The part is the number of those that have at least
1,900 square feet.

To find the number of homes that have at least 1,900 sq ft,
identify the rows that include intervals of 1,900 or more.
To find the number of homes that have at least 1,600 sq ft,
identify the rows that include intervals of 1,600 or more.
Then add the corresponding numbers of homes to find the values of the part and the whole.
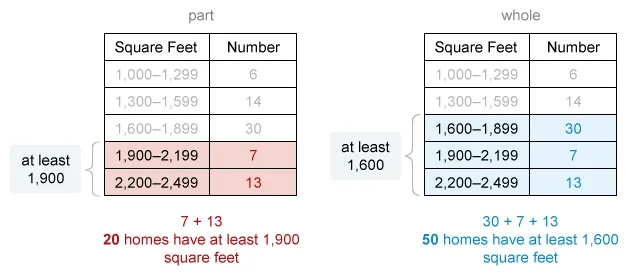
Of the 50 homes that have at least 1,600 square feet, 20 have at least 1,900 square feet.

It is not possible to grid the value , so it is necessary to rewrite to fit the grid. Of the homes that have at least 1,600 square feet, the fraction that have at least 1,900 square feet is .
Things to remember:
A fraction represents a part (numerator) of a whole (denominator).

Question
It is estimated that an average raindrop has a mass of 34 milligrams and falls at a constant speed of 1,200 centimeters per second. How far, in centimeters, would a raindrop of this size fall in 12 seconds?
| A.144,000 | |
| B. 40,800 | |
| C.14,400 | |
| D. 408 |
Explanation
An object moving at a constant speed travels a distance equal to the product of its speed and the time of travel.

It is given that a raindrop falls at a constant speed of 1,200 centimeters per second. To find the distance that the raindrop falls in 12 seconds, plug these values for speed and time into the distance equation.
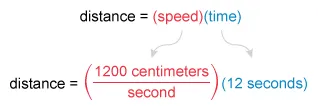
Now cancel units and multiply to find the distance in centimeters.

In 12 seconds, a raindrop with the given speed will travel 14,400 centimeters.
Note: The given mass (34 milligrams) is extra information and is not needed to answer this question.
(Choice A) 144,000 is the distance in millimeters (instead of centimeters) and may result from mistakenly multiplying 12,000 (instead of 1,200) by 12 seconds.
(Choices B and D) 40,800 and 408 may result from mistakenly multiplying the given speed (1,200) or the given time (12) by the given mass (34 grams).
Things to remember:
An object moving at a constant speed travels a distance equal to the
product of its speed and the time of travel.

Question
A garden shop has a display of plants for sale. Each plant is either a flower or a vegetable and is either organic or nonorganic. The probability of randomly selecting a plant that is a flower is 0.4. The probability of randomly selecting a plant that is nonorganic and is a vegetable is 0.1. If the display holds 80 plants, how many are vegetables that are organic?
| A.32 | |
| B.40 | |
| C.48 | |
| D.72 |
Explanation
To find the probability P of a desired event, use the following formula:

Use the given probabilities to find the number of vegetable plants and the number of nonorganic vegetable plants. Then subtract to find the number of organic vegetable plants.
Vegetable plants
The given probability of randomly selecting a plant that is a flower is 0.4.
The number of possible outcomes is the given total
number of plants (80).
The number of desired outcomes is the number of
those plants that are flowers.
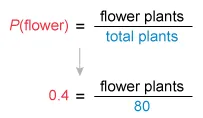
Solve for the number of flower plants.
| Probability | |
| Multiply both sides by 80 to clear the fractions | |
| Simplify |
Of the 80 plants, 32 are flowers and the rest are vegetables.
Subtract to find that there are 80 − 32 = 48 vegetable plants.
Nonorganic vegetable plants
The given probability of randomly selecting a plant that is a nonorganic vegetable is 0.1.
The number of possible outcomes is the total number
of plants (80).
The number of desired outcomes is the number of those
plants that are nonorganic vegetables.
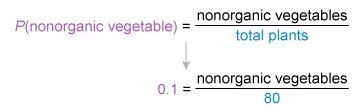
Solve for the number of nonorganic vegetable plants.
| Multiply by both sides by 80 to clear the fractions | |
| Simplify |
There are 8 nonorganic vegetable plants.
There are 48 vegetable plants and 8 of them are nonorganic, so the rest are organic.
Subtract the number of nonorganic vegetable plants (8) from the total number of vegetable plants (48) to find that 48 − 8 = 40 plants are vegetables that are organic.
(Choice A) 32 is the number of plants that are flowers, but the question asks for the number of plants that are vegetables and organic.
(Choice C) 48 is the number of plants that are vegetables, but the question asks for the number of plants that are vegetables and organic.
(Choice D) 72 may result from mistakenly subtracting the number of plants that are vegetable and nonorganic (8) from the total number of plants (80) instead of from the number of plants that are vegetables (48).
Things to remember:
The probability of a desired event is equal to the number of desired
outcomes divided by the total number of possible outcomes.

Alternate Method :
It is also possible to first calculate the probability of randomly selecting an organic vegetable plant and then use the probability formula to find the number of organic vegetable plants.
It is given that the plants are either flower or vegetable. Therefore, the event that a plant is a vegetable is the complement of the event that a plant is a flower.
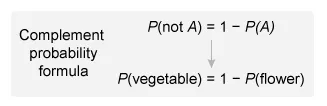
It is given that the probability of selecting a plant that is a flower is 0.4. Plug P(flower) = 0.4 into the complement probability formula and solve for P(vegetable) to find the probability of selecting a plant that is a vegetable.
| P(vegetable) = 1 − P(flower) | Complement formula |
| P(vegetable) = 1 − 0.40 | Plug in P(flower) = 0.4 |
| P(vegetable) = 0.60 | Subtract |
The probability of selecting a plant that is a vegetable is 0.6, and the given probability of selecting a plant that is nonorganic and a vegetable is 0.1.
Every vegetable is either nonorganic or organic, so the probabilities of nonorganic vegetable (0.1) and organic vegetable must add to the probability of vegetable (0.6).

Subtract to find that the probability of selecting a plant that is organic and a vegetable is 0.6 − 0.1 = 0.5.
The probability of selecting a plant that is organic and a vegetable (0.5) is equal to the number of organic vegetables divided by the total number of plants (80). Plug these values into the probability formula.
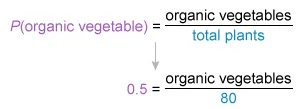
Solve for the number of organic vegetable plants.
| Multiply both sides by 80 to clear the fractions | |
| Simplify |
Of the plants on display, 40 are vegetables that are organic.
Things to remember:
- The complement of an event A is the event that A does NOT occur. The probability that an event A does NOT occur, P(not A), is equal to 1 minus the probability that it does occur, P(A):
P(not A) = 1 − P(A)
- To find the probability of a desired event, use the following formula:

Question
The price of a discounted one-way bus ticket is $54.00. The discounted price is 40% less than the original price of the bus ticket. What was the original price of the bus ticket? (Assume there is no sales tax.)
| A.$21.60 | |
| B.$32.40 | |
| C.$90.00 | |
| D.$135.00 |
Explanation
It is given that the discounted ticket price is 40% less than the original ticket price, so the discounted price $54 is the result of a 40% decrease of the original price. To decrease an amount by p%, multiply it by (proof).
The original price multiplied by is equal to the discounted price. Let the original price be x, and write an equation to relate the original price (x), the given percent decrease (p = 40), and the discounted price (54).
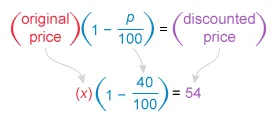
Now solve the equation for x, the original price.
| Simplify: | |
| Multiply both sides by the reciprocal to isolate x | |
| Simplify: |
The original price of the bus ticket was $90.
(Choice A) $21.60 is 40% of the discounted price and may result from mistakenly multiplying $54 by , instead of dividing $54 by .
(Choice B) $32.40 is 60% of the discounted price and may result from mistakenly multiplying (instead of dividing) the discounted amount $54 by .
(Choice D) $135.00 would be the original price if there was a 60% discount (instead of 40%) and may result from mistakenly dividing the discounted price $54 by (instead of ).
Things to remember:
-
A discounted price that is p% less than an original price is equivalent to decreasing the original price by p%.
-
To decrease a value by p%, multiply it by :