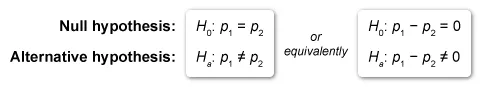AP® Statistics Unit 6 Review and Practice Test
Learning how to use sample data to make evidence-based claims about a population has never been made so easy. With UWorld, you’ll connect AP® Statistics Unit 6 formulas to meaning, practice with exam-style questions, and see how inference turns data into conclusions.
Build Exam-Readiness with Our AP Statistics Unit 6 Review
From guessing to reasoning, UWorld’s AP Statistics Unit 6 review helps you understand how proportions tell stories about real-world populations, covering opinion polls to genetics. This review course is everything you need to ace the exam, as every video, guide, and question is expertly curated, so you learn to calculate, interpret, and explain like a statistician ready for the AP Exam.
Visualize Inference in Real Time
Statistics without understanding the logic leaves you nowhere. Our video library takes a step-by-step approach through significance tests, p-values, confidence intervals, and how sample data supports or challenges the hypothesis. With visual demonstrations, each short and focused video breaks down complex big ideas of the unit into lessons that you’ll remember.
Turning Proportions Into Proof
Let’s go beyond memorizing formulas through dense textbooks and connect the logic with UWorld’s AP Stats Unit 6 study guides. Every section reinforces the why behind the how, interacting with you through visual examples and guided notes, making you an expert by exam day.
Ace the Race with Realistic Practice Questions for Unit 6
Question
A researcher found that a large-sample 95 percent confidence interval for the proportion of subscriptions that are not canceled before the end of a free trial period is (0.056, 0.124). What is the point estimate for the proportion of subscriptions that are not canceled before the end of the free trial period from which this interval was constructed?
| A. 0.034 | |
| B. 0.068 | |
| C. 0.090 | |
| D. 0.180 | |
| E. It cannot be determined from the information given. |
Hint:
A confidence interval has the general form: point estimate ± margin of error.
Explanation
A confidence interval (CI) adds and subtracts a margin of error from a point estimate (sample statistic), so the point estimate is the midpoint of the interval.
It is given that the CI is (0.056, 0.124), so the point estimate must be the midpoint value between 0.056 and 0.124. Eliminate Choices A and D because those values are either below 0.056 or above 0.124.
The midpoint of an interval is equal to the sum of its endpoints divided by 2. To find the midpoint of the given interval, add the lower boundary (0.056) to the upper boundary (0.124) and then divide by 2.
Therefore, the point estimate for the proportion of subscriptions that are not canceled before the end of the free trial period from which this interval was constructed is 0.090.
Note: Point estimates are always at the center of the confidence interval (except in rare cases that will not appear on the exam).
(Choices A and B) These choices may result from mistakenly subtracting the lower boundary from the upper boundary, but it is necessary to add them together and then divide that result by 2.
(Choice D) 0.180 may result from not dividing the sum of the lower and upper boundaries by 2.
(Choice E) This choice may result from a misconception about how an interval is constructed. The point estimate is always contained in the interval constructed from the same sample data.
Things to remember:
A confidence interval adds and subtracts a margin of error from a point estimate (sample statistic), so the point estimate is the midpoint of the interval (except for rare cases that do not appear on the AP exam).
Question
A marketing firm is asked to estimate the proportion of homes in a city with landline phones. A random sample of 150 adult residents were surveyed to determine whether they have a landline phone in their home. Of the people surveyed, 35 percent responded that they have a landline phone. The firm decides to construct a 99 percent confidence interval to estimate the true proportion of homes in the city with landline phones. Assuming all conditions for inference are met, which of the following is closest to the critical value for the 99 percent confidence interval?
| A. 1.645 | |
| B. 1.960 | |
| C. 2.326 | |
| D.2.576 | |
| E. 2.609 |
Hint:
A critical value is a boundary used to identify the middle C% of a probability distribution, where C% is the confidence level of a confidence interval.
Explanation
A critical value is a boundary used to identify the middle C% of a probability distribution, where C% is the level of confidence of a confidence interval (CI). It is the multiplier that makes a CI wide enough to have C% confidence.
A marketing firm will construct a CI to estimate the true proportion p of city homes with landlines. When conditions for inference are met, the CI for a proportion is a z-interval, and the critical value is a z-score (z*).
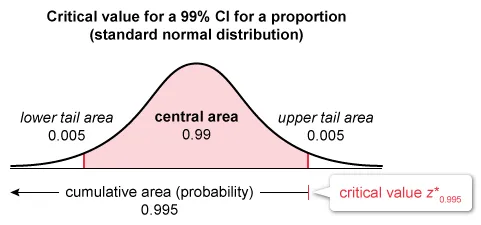
The critical value z* of a 99% CI for p is the z-score that captures the central 99% (and accumulates 99.5%) of the area under the standard normal distribution (z-distribution). The notation for the critical value z* is z0.995.
| To find z0.995, first locate the inverse normal distribution (invNorm) function on a calculator. Input the area under the curve for a 99% CI (cumulative area = 0.995), the mean (0) and standard deviation (1) of the standard normal distribution, and then specify the required tail area (left). |
The answer choice closest to the critical value for the 99% CI for the proportion of adults living in the city who have landline phones is z* = 2.576.
Note: It is possible to determine the critical z-score (z*) with the normal distribution table (see table).
(Choice A) 1.645 results from mistakenly determining the critical value for a 90% CI (z0.95 = 1.645) instead of the critical value for a 99% CI (z0.995 = 2.576).
(Choice B) 1.960 results from mistakenly determining the critical value for a 95% CI (z0.975 = 1.960) instead of the critical value for a 99% CI (z0.995 = 2.576).
(Choice C) 2.326 results from mistakenly determining the critical value for a 98% CI (z0.99 = 2.326) instead of the critical value for a 99% CI (z0.995 = 2.576).
(Choice E) 2.609 results from mistakenly determining the critical value of the CI based on t-distribution with 150 − 1 = 149 degrees of freedom (t149, 0.995 = 2.609) rather than the normal distribution (z0.995 = 2.576).
Things to remember:
- Use a z-interval to construct a confidence interval (CI) for a population proportion p when the conditions for inference are met.
- The critical value z* for a C% CI for p is the z-score that captures the central C% of the area under the standard normal distribution.
Question
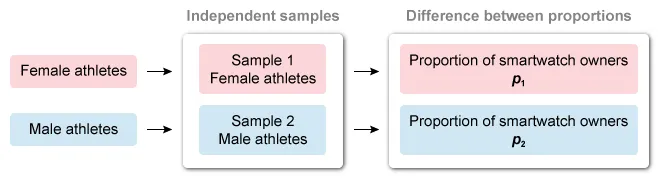
Researchers conducted a survey of 210 randomly selected female professional athletes and 290 randomly selected male professional athletes in a large city. The athletes were asked whether they owned a fitness smartwatch. A total of 180 female athletes and 261 male athletes reported owning a fitness smartwatch. An appropriate hypothesis test was conducted to investigate whether there was a difference between female and male professional athletes in their ownership of a fitness smartwatch. Assuming that conditions for inference are met, is there convincing statistical evidence of a difference between the two population proportions at the significance level of 0.05 ?
| A. No, because the probability of observing a difference at least as large as the sample difference, if the two population proportions are the same, is greater than 0.05. | |
| B. No, because the probability of observing a difference at least as large as the sample difference is less than 0.05. | |
| C. Yes, because the probability of observing a difference at least as large as the sample difference, if the two population proportions are the same, is less than 0.05. | |
| D. Yes, because the probability of observing a difference at least as large as the sample difference is greater than 0.05. | |
| E. Yes, because the sample proportions are different. |
Hint:
Identify the appropriate test and hypotheses, then conduct the test and compare its p-value to the given significance level α to evaluate the statistical evidence.
Explanation
To draw a conclusion about the given data, first identify the appropriate test and hypotheses. Then conduct the test and compare its p-value to the given significance level α.
Researchers selected two independent random samples (female and male athletes) to determine whether there is a difference in the proportion of smartwatch owners between the populations.
The appropriate hypothesis test must evaluate whether there is a difference between two population proportions, so the hypotheses are:
When conditions for inference are met, the hypothesis test that determines whether there is a difference between proportions from two independent samples is the two-sample z-test for proportions.
Notice that Ha is two-sided, so conduct a two-sided, two-sample z-test for proportions and calculate its p-value. Then compare the p-value to the significance level α.
| Locate the two-sample z-test for proportions (2-PropZTest) command on a calculator. Input the given values of the sample statistics for each sample (x1 = 180, n1 = 210, x2 = 261, and n2 = 290), and select the two-sided alternate hypothesis, Ha: p1 ≠ p2. |
If the p-value ≤ α, there is convincing evidence that Ha is true (difference between proportions).
If the p-value > α, there is not convincing evidence that Ha is true (no difference between proportions).
The p-value is 0.143, which is greater than 0.05 (the given significance level α), so there is not convincing evidence in favor of Ha.

The p-value assumes H0 is true, so the p-value for the two-sample z-test for proportions assumes that the two population proportions are the same.
| Therefore, there is not convincing evidence because the probability of observing a difference at least as large as the sample difference, if the two population proportions are the same, is greater than 0.05. |
(Choices B, C, and D) The p-value is greater than (not less than) the given significance level (0.05), so there is no convincing statistical evidence to conclude that there is a difference between the population proportions.
(Choice E) An apparent difference between two sample proportions does not provide convincing statistical evidence of a difference. It is necessary to conduct a hypothesis test to evaluate the statistical evidence.
Things to remember:
- A two-sample z-test for the difference of proportions compares proportions of two independent samples.
- The p-value is the probability of finding the observed or more extreme results when the null hypothesis H0 is true. The definition of "extreme" depends on the direction specified by the alternative hypothesis Ha.
- To determine whether there is convincing statistical evidence against a null hypothesis H0 and in favor of an alternative hypothesis Ha, compare the p-value to the significance level α.
- If p-value ≤ α, there is convincing evidence in favor of Ha.
- If p-value > α, there is not convincing evidence in favor of Ha.

Keep Your Preparation on the Run
Tackle practice questions on the ride home from a game, review topic videos between classes, or dive into a study guide while waiting for friends at the coffee shop. Everything you need for AP Statistics Unit 6 review is always at your fingertips with the UWorld app.
Stand Out
with a Top Score on the AP Statistics Exam
Finish your AP Statistics Unit 6 review and continue mastering all units with UWorld. Complete our AP Statistics full review course to boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Stats Videos
- Print & Digital Study Guide
- 1300+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Statistics Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What are the main topics covered in AP Statistics Unit 6: Inference for Categorical Data: Proportions?
AP Statistics Unit 6 focuses on statistical inference for categorical data, specifically proportions. Students learn to construct and interpret confidence intervals, perform one- and two-sample z-tests, and interpret p-values to make data-driven conclusions. This unit also introduces Type I and Type II errors, helping you understand how statistical decisions can lead to different real-world consequences.
Core topics include:
- Confidence intervals for one and two proportions
- Significance testing for population proportions
- Interpreting p-values and significance levels
- Understanding Type I/II errors in hypothesis testing
- Comparing differences between proportions and evaluating claims
Each concept builds on prior probability and sampling knowledge, forming the foundation of all later inference topics. UWorld’s AP Statistics unit 6 review ensures you can confidently use sample data to justify conclusions and think like an AP grader.
How are confidence intervals and hypothesis tests related in AP Statistics Unit 6?
Confidence intervals and hypothesis tests are two sides of the same reasoning framework in AP Statistics Unit 6. Both use sample data to infer truths about population proportions. The AP Stats Unit 6 review introduces this connection early, showing how overlapping or non-overlapping intervals reflect statistical significance. Questions on both topics appear in AP Stats Unit 6 MCQs and FRQs. Study them together rather than as separate tools. Use the AP Stats Unit 6 study guide to map how each part aligns: null and alternative hypotheses, confidence level, and test statistics.
Practice rewriting confidence interval interpretations as test conclusions and vice versa. This exercise helps recognize the logic behind inference and strengthens response precision. UWorld study guides often integrate both methods in a single activity. By toggling between z-intervals and z-tests, learners see how confidence intervals predict hypothesis outcomes, reinforcing conceptual unity without redundancy.
What are the types of Questions that appear on the AP Stats Unit 6 Test?
The AP Statistics Unit 6 exam features both multiple-choice (MCQs) and free-response questions (FRQs) that test your understanding of inference for categorical data, specifically proportions. Expect to construct and interpret confidence intervals, perform one and two-sample z-tests, and interpret p-values to justify statistical claims. Questions will often require you to identify when conditions for inference are met and explain the meaning of your conclusions in plain language.
MCQs challenge your ability to apply logic quickly across different scenarios, like distinguishing between a significance test and a confidence interval question. At the same time, FRQs demand written explanations, reasoning, and full contextual conclusions. You may also be asked to evaluate potential Type I and Type II errors and their impact on real-world decisions. Each UWorld AP Stats Unit 6 review question replicates this structure, training you to think and write like an AP scorer. You’ll build speed, accuracy, and statistical clarity with consistent timed practice.
How should I prepare for an AP Statistics Unit 6 exam?
To prepare for the AP Stats Unit 6 exam, start by reviewing probability and sampling distributions from earlier units. These form the groundwork for inference. Then focus on interpreting confidence intervals and significance tests conceptually, not just mathematically.
Here’s an expert-recommended study strategy:
- Watch short AP Stats Unit 6 videos that demonstrate inference visually.
- Take timed practice test sets to simulate a real exam environment.
- Practice explaining what a p-value or confidence interval means in plain English.
- Review examples of Type I and Type II errors using real-world scenarios.
As you study, connect the math to logic by asking, “What does this tell me about the population?” UWorld’s AP Stats Unit 6 review bridges that gap with visual lessons and detailed question explanations. The more you focus on reasoning, not rote steps, the easier it becomes to write strong FRQs and interpret MCQs accurately.
How can I improve my score on the FRQs and MCQs for Unit 6?
Raising your score on the Free-Response Questions (FRQs) and Multiple-Choice Questions (MCQs) in AP Statistics Unit 6 requires mastering and applying inference concepts under pressure. FRQs test structured reasoning and communication, while MCQs demand conceptual fluency and speed. You need a balance of clarity, logic, and repetition in practice to improve.
Focus on these proven strategies:
For FRQs: Always define hypotheses clearly and in context, verify all conditions (randomness, independence, and normality), and show each step of your work. Interpret your confidence intervals, p-values, and test results in complete sentences, linking conclusions to the scenario. Include an explanation of Type I and Type II errors where relevant.
For MCQs: Identify common patterns, such as one- vs. two-proportion z-tests, and review every explanation, especially for wrong answers. Practice timed quizzes to sharpen decision-making.
UWorld’s AP Stats Unit 6 review resources combine MCQ and FRQ-style practice into a seamless learning experience. Each explanation breaks down reasoning, not just results, helping you understand why answers work. Over time, you’ll develop statistical intuition, test stamina, and the confidence to handle any inference question the AP exam throws your way.
What is the one practice test format that works best for AP Stats Unit 6?
A strong AP Stats Unit 6 practice test or AP Statistics Unit 6 practice test should mirror the real exam in both structure and timing. Each set needs a balanced mix of one-proportion and two-proportion confidence intervals and z-tests, including a few “condition traps” that force you to verify assumptions before proceeding. If a particular concept feels weak, rotate in a short Unit 6 AP Stats practice test that targets just that area. For quick reinforcement, use a compact AP Stats Unit 6 practice test PDF for short sessions, then return to the full online format for solutions and analytics.
Keep each practice session structured and deliberate. Begin with a brief plan outlining what you’ll focus on, and close with a short reflection identifying what improved and what still feels uncertain. When your accuracy stabilizes, simulate a complete exam under timed conditions that combine MCQs and one FRQ. Always write answers with correct units and real-world context. The objective is not memorizing steps but building a repeatable, confident process that performs reliably under exam pressure.
What are the common reasoning mistakes students make in AP Statistics Unit 6?
Common reasoning errors in AP Statistics Unit 6 include mixing sample statistics with population parameters, misinterpreting p-values, and failing to verify inference conditions. These issues appear across AP Stats Unit 6 MCQs, FRQs, and progress check MCQs, often costing students clarity points on responses. To avoid them, use your AP Stats Unit 6 study guide to review the conditions for inference before every practice session.
When completing AP Statistics Unit 6 progress check MCQs, pause after each question and restate your logic aloud. This practice makes you aware of where reasoning shortcuts occur. Reviewing missed problems in an AP Stats Unit 6 practice test helps track recurring mistakes over time. UWorld practice questions target these misunderstandings by embedding subtle traps in problem statements. Their step-based feedback highlights where reasoning diverges from statistical principles, allowing you to correct misconceptions before they become habits.
Are there any free resources available for AP Statistics Unit 6?
Yes. UWorld offers a free trial for AP Statistics Unit 6 that gives you access to the practice questions, interactive study guides, and short-video lessons on confidence intervals, z-tests, p-value interpretation, and all core topics of the unit. You’ll also find snippets from the AP Stats Unit 6 study guide, showing how visuals simplify formulas and connect them to real data.
These free previews provide an understanding of how UWorld makes complex topics accessible without overwhelming jargon or extraneous noise. Try a few to see how our approach transforms formulas into understanding. Once you’re ready, full access unlocks hundreds of exam-style questions, visual breakdowns, and timed quizzes to help you build speed and confidence for the real test. Besides, combining UWorld’s review with Khan Academy and College Board resources can give you an additional perspective, while using UWorld as the primary base for the most efficient preparation.
Where can I find a good study guide for AP Statistics Unit 6?
UWorld provides the best study guide for AP Statistics Unit 6. It’s designed for quick reference and deep understanding, breaking down inference into visual and logical steps. Each topic – confidence intervals, significance testing, and Type I/II errors – is illustrated with examples and conditions. Developed by experts, the guide is a good departure from the dense textbooks and presents opportunities to test yourself and ensure that what you learn stays.
Here’s what you get in the AP Statistics Unit 6 study guide:
- Summaries of z-test formulas and assumptions
- Interactive visuals breaking down concepts and formulas
- Notes on one- vs. two-sample proportion inference
- Step-by-step explanation
- Tips on explaining p-values clearly in FRQs
The guide is linked directly to matching AP Stats Unit 6 practice test sets, so you can immediately test what you’ve learned. Instead of flipping between notes and textbooks, you’ll have everything in one streamlined system built to save time and boost comprehension before exam day.
Are there practice tests specifically for AP Stats Unit 6?
Yes. UWorld provides comprehensive AP Statistics Unit 6 practice test collections that simulate real AP exam structure and difficulty. Each test includes one- and two-sample z-tests, confidence interval problems, and interpretation-based FRQs.
UWorld’s Practice Test Features:
- AP-aligned question styles for MCQs and FRQs
- Step-by-step, annotated solutions for every problem
- Built-in performance analytics to track improvement
- Adjustable quiz mode for focused review
Practicing with UWorld helps you spot patterns, reinforce inference logic, and understand how to apply statistics to real-world categorical data. Because every explanation connects concept to calculation, you’ll build the analytical mindset needed to perform under pressure. Once you can explain why your answer is correct, you’re already thinking like an AP grader.
When should I begin preparing for the AP Stats Unit 6 test?
Start preparing for AP Statistics Unit 6 about four weeks before the scheduled test. Early study ensures space for both concept development and repeated testing. The AP Stats Unit 6 review sequence should begin with sampling distributions, move into confidence intervals, and finish with hypothesis testing and interpretation.
Week 1-2: Study key formulas and practice conceptual questions from the AP Stats Unit 6 study guide.
Week 3: Take a set of AP Statistics Unit 6 progress check MCQs.
Week 4: Transition into full-length AP Stats Unit 6 practice tests.
This structure promotes steady recall rather than cramming. UWorld study guides align with this pacing by presenting concepts and practice in the same order, helping students reinforce understanding through spaced repetition.
Learn More About Specific Unit
Exploring One-Variable Data
Exploring Two-Variable Data
Collecting Data
Probability, Random Variables, and Probability Distributions
Sampling Distributions
Inference for Quantitative Data: Means
Inference for Categorical Data: Chi-Square
Inference for Quantitative Data: Slopes