AP® Statistics Unit 4 Review and Practice Test
Probability doesn’t have to feel like a puzzle you can’t solve. AP® Statistics Unit 4 connects logic with data to help you understand how chance, outcomes, and distribution shape real-world results. Solving this puzzle becomes easy when you’ve the right tools to guide you through the unit. With UWorld’s AP Stats Probability Review, you get an integrated platform with engaging video lessons, interactive study guides, and real-time practice questions to ace the exam.
Achieve a Full-Score Without the Fuss of Losing on Probability
You’re at the intersection of math and intuition, a crossroad many struggle with. But not anymore! With our AP Statistics Probability review, we simplify every formula, distribution, and concept using simple examples that make sense. Move from guessing outcomes to predicting probabilities with accuracy, with a step-by-step structure to dodge any challenge the AP Probability exam throws.
Probability in Action
You can’t just memorize sequences and get through the exam; you’ve got to see them unfold in every scenario. Our AP Stats Probability review uses visual simulations and real-world examples to bring the math to life. From choices to sequences to variables, everything is covered through short-targeted lessons that break these big ideas into easy-to-grasp pieces, helping you go beyond rote learning and actually apply them.
Turn Numbers into Meaning
Connecting probability rules to real applications lets you identify random variables confidently, use probability models, and apply distribution formulas. Our interactive AP Stats Unit 4 study guides give you the confidence by making the review efficient and intuitive using annotated visuals, graphs, and solved examples.
Train Yourself On Exam-Level Probability Questions
Question
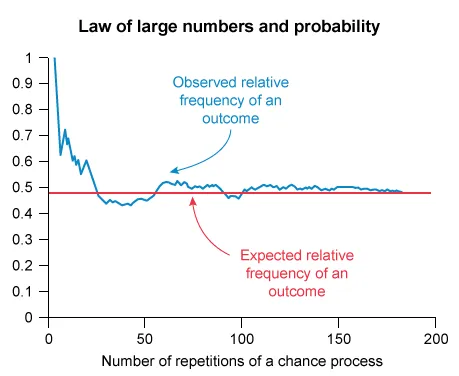
In a simulated game, the roll of a fair six-sided die is randomized according to a computer. The computer software was written to guarantee that rolls are independent and that the probability of the number 2 landing faceup is equal to . If the computer software is functioning correctly, which of the following statements must be true?
-
In repeated simulations, the relative frequency with which the number 2 will land faceup in the long run is equal to .
-
If after several repetitions the relative frequency of the number 2 landing faceup is less than , then the probability that the number 2 lands faceup will increase for future simulations.
-
The relative frequency will equal the probability if the number of simulations is greater than 30.
| A. I only | |
| B. II only | |
| C. I and II only | |
| D. I and III only | |
| E. I, II, and III |
Hint:
Probability is the relative frequency of an outcome of a chance process in the long run.
Explanation
A probability is the relative frequency of an outcome of a chance process when the process is repeated many times (long-run frequency).
The law of large numbers states that as the number of independent trials of a chance process increases, the observed relative frequency of an outcome gets closer to its expected relative frequency (probability).
When the number of trials is small, the relative frequency may differ from the true expected relative frequency due to random variation. Determine whether each statement is true.
Statement I: In repeated simulations, the relative frequency with which the number 2 will land faceup in the long run is equal to .
If the computer software is functioning correctly, the probability that the number on the fair six-sided die that lands faceup is 2 is equal to .
This statement is true because the law of large numbers guarantees that the probability of an event is equal to the expected long-run frequency of that event. It is possible to eliminate Choice B.
Statement II: If after several repetitions the relative frequency of the number 2 landing faceup is less than , then the probability that the number 2 lands faceup will increase for future simulations.
If the computer software is functioning correctly, then the simulated rolls are independent. Events are independent if the occurrence of one event does not impact the probability of the other.
This statement is false because the probability (likelihood) that the number 2 lands faceup is not impacted by earlier rolls of the die. It is possible to eliminate Choices B, C, and E.
Statement III: The relative frequency will equal the probability if the number of simulations is greater than 30.
The law of large numbers guarantees that the relative frequency will approach the true probability as the number of repetitions increases, but it may or may not be exactly equal to the probability.
This statement is false because it is not certain that the observed relative frequency of the number 2 will be equal to the true probability, for any number of simulations. It is possible to eliminate Choices D and E.
Therefore, only Statement I must be true.
Things to remember:
A probability is the relative frequency of an outcome of a chance process when the process is repeated many times (long-run frequency).
The law of large numbers states that as the number of independent trials of a chance process increases, the observed relative frequency of an outcome gets closer to its expected relative frequency (probability).
Question
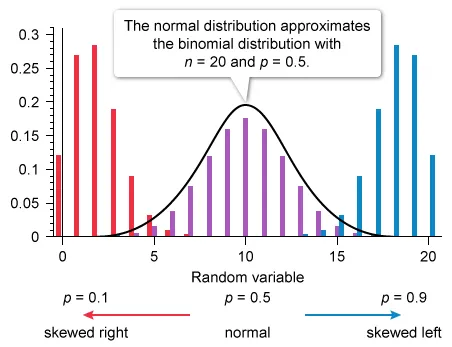
Which of the following graphs represents a binomial probability distribution with parameters n = 16 and p = 0.50 ?
A.  |
|
B. 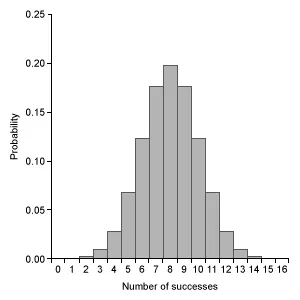 |
|
C. 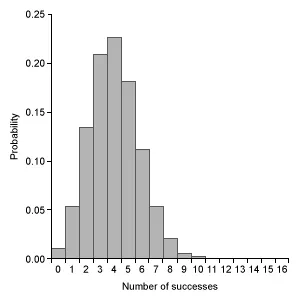 |
|
D.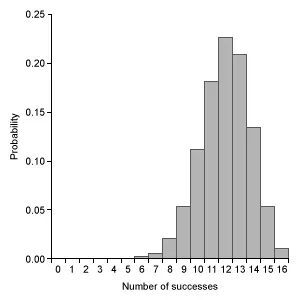 |
|
E. 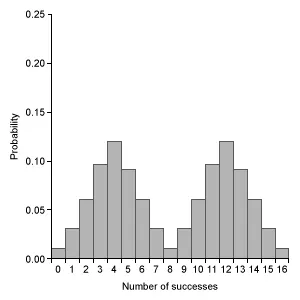 |
Hint:
Consider the mean and standard deviation of the binomial distribution: μx = np and .
Explanation
A binomial probability distribution models the probability of the number of successes of a binomial random variable that meets the conditions of a binomial setting (BINS).
When the parameters of a binomial distribution meet certain conditions, the normal distribution can approximate a binomial distribution.
Eliminate Choice A because a binomial distribution with probability of success p = 0.5 is approximated by a normal distribution. Eliminate Choice E because binomial distributions cannot be bimodal.
Notice that the remaining graphs each have a different center, so calculate the mean μx of a binomial distribution with n = 16 and p = 0.5 (μx = np).
| μx = np | Mean of binomial variable X |
| μx = 16 × 0.50 | Plug in values |
| μx = 8 | Simplify |
The mean μx of the given distribution is 8. The graph in Choice B is the only distribution with a single peak at 8.
Note: It is also possible to calculate the standard deviation of the distribution to help identify the correct graph.
(Choices A and E) The binomial distribution with n = 16 and p = 0.50 is approximated by a normal distribution, but Choice A is a geometric distribution and Choice E is bimodal.
(Choice C) This graph is slightly skewed to the right and centered at 4, but the graph of a binomial distribution with n = 16 and p = 0.50 is approximately normal and centered at 8.
(Choice D) This graph is slightly skewed to the left and centered at 12, but the graph of a binomial distribution with n = 16 and p = 0.50 is approximately normal and centered at 8.
Things to remember:
- The binomial distribution with parameters n and p has mean (expected value) μx = np and standard deviation
- When p = 0.5, the binomial distribution is approximated by the normal distribution.
Question
A cereal company launches a superhero promotion and decides to include 1 of 5 different superhero figurines in each box of their kids' cereal. The company states that each of the 5 figurines is equally likely to appear in any box of cereal. A statistics student decides to run a simulation to investigate how many boxes of cereal it would take to collect all of the figurines. One trial of the simulation is described by the following steps.
Step 1: Label 5 different tokens 1 through 5 and assign each number to represent a different figurine.
Step 2: Randomly select 1 token at a time with replacement until the 5 different numbers are collected.
Step 3: Record the number of tokens necessary to collect the 5 different tokens.
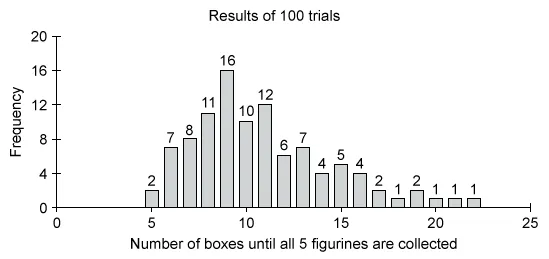
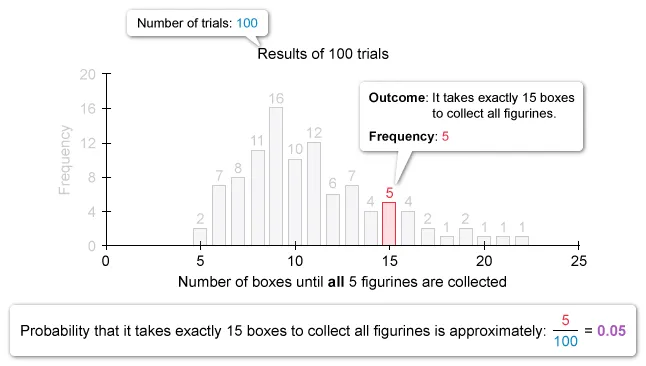
The results of 100 trials of the simulation are shown in the following histogram.
Based on the results of the simulation, which of the following statements is true?
| A. The simulation suggests that the approximate probability that it will take exactly 5 boxes of cereal to collect all 5 figurines is greater than the probability that it will take more than 20 boxes of cereal. | |
| B. The simulation suggests that the probability that it will take less than 10 boxes of cereal to collect all 5 figurines is about 0.55. | |
| C. The simulation suggests that it will take more than 18 boxes of cereal to collect all 5 figurines approximately 5% of the time. | |
| D. The simulation suggests that it will take more than 19 boxes of cereal to collect all 5 figurines approximately 95% of the time. | |
| E. The simulation suggests that it will take at least 22 boxes of cereal to collect all 5 figurines. |
Hint:
To find the relative frequency of a particular outcome in a simulated random process, identify the frequency (count) of the outcome of interest and divide that value by the total number of trials in the simulation.
Explanation
Simulation is the repetition of a random process that closely matches a real-world random event. In a simulation, the relative frequency of each outcome in a random process approximates its probability.
To find the relative frequency of a particular outcome in a simulated random process, identify the frequency (count) of the outcome of interest and divide by the total number of trials in the simulation (ex. 100).
Use the given simulation to analyze each answer choice and determine which statement is true. Notice that it takes more than 18 (19 or more) boxes of cereal to collect 5 different figurines in 5 out of 100 trials.
Therefore, the statement that is true is:
| The simulation suggests that it will take more than 18 boxes of cereal to collect all 5 figurines approximately 5% of the time. |
(Choice A) The approximate probability that it will take exactly 5 boxes to collect all 5 figurines is 0.02, which is equal to (not greater than) the approximate probability that it will take more than 20 boxes (also 0.02).
(Choice B) Based on the simulation, the probability that it will take less than 10 boxes to collect all 5 figurines is 0.44, not 0.55.
(Choice D) Based on the simulation, the probability that it will take more than 19 (20 or more) boxes to collect all 5 figurines is 3%, not 95%.
(Choice E) The simulation includes trials where the number of boxes required to collect all 5 figurines was less than 22, so it does not suggest that there must be at least 22 boxes of cereal to collect all 5 figurines.
Things to remember:
- Simulation is the repetition of a random process that closely matches a real-world random event. In a simulation, the relative frequency of each outcome approximates its probability.
- The relative frequency of a particular outcome in a simulated random process is equal to its frequency (count) divided by the total number of trials in the simulation.
Stand Out
with a Top Score on the AP Statistics Exam
Finish your AP Statistics Unit 4 review and continue mastering all units with UWorld. Complete our AP Statistics full review course to boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Stats Videos
- Print & Digital Study Guide
- 1300+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Statistics Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What are the main topics covered in AP Statistics Unit 4: Probability, Random Variables, and Probability Distributions?
AP Statistics Unit 4 is where statistics start to feel like prediction. This unit connects randomness to measurable outcomes using the logic of probability, random variables, and probability distributions. Understanding how uncertainty behaves in real-world scenarios is what makes this unit both challenging and rewarding.
Some of the topics covered are:
- Using simulation to estimate probabilities
- Random variables and probability distributions
- Calculating the probability of a random event
- Binomial and Geometric distributions
Together, these concepts explain how we quantify uncertainty and anticipate outcomes, whether it’s the chance of drawing a red card or the probability of a system failure. The AP Statistics Unit 4 probability review also introduces the logic behind expected value and variance, which help predict long-term patterns.
UWorld’s AP Stats Unit 4 review lessons simplify formulas through real-life examples and detailed step-by-step reasoning. Once you understand how to model randomness mathematically, inference and decision-making in later units become much easier. This unit isn’t just about math; it’s about learning how to reason with uncertainty like a statistician.
Where can I find a good study guide for AP Statistics Unit 4?
UWorld’s AP Stats Unit 4 study guide is perfect for all types of learners. Its interactive nature summarizes the most important formulas, concepts, and distribution properties with visuals that stick. It’s designed by experts for quick and targeted review, covering clear definitions and real-world applications. Coupled with digital flashcards and a progress dashboard, the study guide becomes the best way to reinforce understanding and strengthen weak areas before the test.
Here’s what you get with UWorld’s AP Stats Unit 4 guide:
- Clear definitions and examples for probability rules and random variables.
- Step-by-step instructions on using binomial and geometric distributions.
- Quick summaries of essential formulas.
- Real-world examples that connect probability theory to applied reasoning.
The study guide covers all this, presenting probability, expected value, and distribution properties through clear visuals and real AP-style examples. You can review definitions, test your recall with questions, and instantly see detailed explanations for each solution. Its interactive layout helps you practice as you read, turning theory into muscle memory. By pairing the study guide with UWorld’s review and timed practice, you can bridge the gap between content understanding and exam performance. It’s built to make AP Stats Unit 4 probability review straightforward, intuitive, and high-yield—everything you need before tackling the real test.
How should I prepare for an AP Statistics Unit 4 exam?
Preparing for the AP Statistics Unit 4 exam is all about developing conceptual accuracy and applied confidence. This unit connects probability theory to real-life randomness—so your goal isn’t just to memorize formulas but to understand what they mean and when to use them.
Here’s an efficient plan:
- Start by mastering the basic rules of probability—addition, multiplication, and independence.
- Watch videos explaining random variables, expected value, and probability distributions in real-world contexts.
- Practice calculating probabilities using tables, trees, and the binomial and geometric formulas.
- Take timed AP Stats Unit 4 practice tests to mirror exam conditions and test recall under pressure.
After each session, review what went wrong and repeat any necessary questions. UWorld’s AP Statistics Unit 4 probability review helps you focus on logic as to why a rule applies and how it fits the question’s structure. By using its step-by-step explanations, you’ll learn to see probability as a story of cause and chance, not a list of equations. When you can explain why a distribution fits or why two events are independent, you’re not just prepared but ready to think statistically, which is exactly what the exam rewards.
Are any free resources available for AP Statistics Unit 4?
Yes. UWorld offers several free resources as part of its 7-day trial for the AP Statistics Unit 4: Probability, Random Variables, and Probability Distributions review. It’s designed to help you understand how probability connects to real-world data and how random variables predict outcomes through engaging, guided learning.
During the trial, you can explore:
- Video lessons explaining core probability rules and distribution logic.
- Interactive simulations showing how random variables behave across trials.
- Practice questions that walk you through binomial and geometric distributions.
- Visual explanations of expected value and variance.
Each free resource allows you to experience UWorld’s “watch, read, and practice” method, which makes abstract concepts such as conditional probability or expected outcomes feel intuitive. You can also compare your performance with real AP-style questions, seeing how exam phrasing connects to classroom concepts. Once the trial ends, upgrading unlocks full access to the complete AP Stats Unit 4 review, with deeper coverage, detailed solutions, and downloadable study materials. If you’re new to AP Stats probability review, this free access gives you a risk-free head start, helping you grasp probability reasoning before committing long-term.
How can I improve my score on the Free-Response Questions (FRQs) for Unit 4?
To improve your FRQ performance for AP Statistics Unit 4, focus on writing with clarity, context, and statistical reasoning. FRQs often test whether you can interpret randomness logically, not just calculate formulas. They reward explanation and structure as much as correct math.
Here’s what high-scoring FRQs always include:
- Clear definitions of random variables and what they represent.
- Every calculation step, even intermediate ones.
- Explanations of binomial or geometric distribution reasoning.
- Final conclusions stated in the context of the question.
UWorld’s AP Stats Unit 4 FRQ practice sets model this perfectly. Each question mirrors real exam prompts, while expert explanations show how graders expect you to justify probability logic in words. The best approach is to think narratively tell the story of the data. Describe what randomness means in the question’s scenario, then use the right probability rule to support your point.
When your reasoning reads smoothly, you’ll align with the exact scoring patterns AP graders look for. UWorld’s feedback makes that consistency second nature before exam day.
What is the "Probability, Random Variables, and Probability Distributions" unit's weight on the AP Statistics exam?
AP Statistics Unit 4 accounts for roughly 10-20% of your total AP Statistics exam score, which means about one out of every five or six questions touches probability or random variables directly. That’s a major portion of the test, and its ideas also reappear in other units, so understanding this unit thoroughly pays off multiple times over.
Probability is the foundation for inference and sampling, both of which dominate later exam sections. Students who take time to master AP Stats Unit 4 probability review early usually find hypothesis testing, expected value, and distribution-based questions easier later.
UWorld’s AP Statistics probability lessons make these abstract topics practical by showing how random events and expected values predict outcomes in business, science, and daily life. You’ll also see how binomial distributions model repeated successes and how geometric logic applies to “first success” events.
These ideas cross over into every major exam unit; nailing them now is like securing free points later. A strong understanding of Unit 4 fosters mathematical intuition, which drives your confidence throughout the entire AP Statistics exam.
How can I improve my score on the Multiple-Choice Questions (MCQs) for Unit 4?
Improving your score on the AP Statistics Unit 4 MCQs comes down to pattern recognition, reasoning speed, and accuracy under pressure. These questions test your ability to decide which rule, formula, or concept applies in just seconds, so the more familiar you are with phrasing and traps, the higher your score climbs.
Here’s a proven strategy:
- Focus on concept recognition, not memorization. The test rarely repeats numbers, but it repeats logic.
- Review probability rules, random variables, and binomial and geometric distributions daily until you can identify them by phrasing.
- Take short, timed sets of AP Stats Unit 4 multiple-choice questions and track which concepts slow you down.
- Analyze every explanation, especially wrong answers, this is where the most learning happens.
UWorld’s AP Statistics Unit 4 probability review offers timed MCQ drills that replicate the exact exam structure. Each question includes detailed reasoning for why one answer works and why others don’t. Over time, you’ll start predicting question types before you even finish reading. That’s how real exam fluency develops.
The key is repetition: practice until common traps, such as misinterpreting independence or using the wrong distribution, feel obvious. The students who score 5 don’t rush; they recognize structure instantly. UWorld’s focused MCQ practice helps you get there efficiently, making accuracy your habit rather than your goal.
Can I find practice tests specifically for AP Stats Unit 4?
Yes. You can find full-length AP Statistics Unit 4 practice tests within UWorld’s review, designed to replicate the pacing, difficulty, and logic of the real AP Statistics exam. Each practice test targets the “Probability, Random Variables, and Probability Distributions” unit, allowing you to isolate and strengthen weak areas before moving on.
Here’s what these practice sets include:
- A mix of MCQs and FRQs based entirely on AP Stats probability formulas and real-world scenarios.
- Step-by-step breakdowns explaining why each solution works, not just what’s correct.
- Questions that test binomial, geometric, and continuous distributions in depth.
- Built-in analytics that track performance across topics like expected value, random variables, and independence.
UWorld’s AP Stats Unit 4 practice tests recreate the actual test environment, timed sections, progress tracking, and instant explanations, so you develop both endurance and insight. Practicing in this simulated setting builds automatic reasoning under exam stress. Every question teaches you how to connect theory to application. The more you repeat this cycle of practice, analyze, and refine, the better your instincts become. By exam day, you’ll know exactly how to approach probability-based questions with confidence, clarity, and speed.
How can I apply probability concepts from Unit 4 to real-world problems?
One of the best parts of AP Statistics Unit 4 is realizing how probability isn’t just math; it’s a decision-making tool used everywhere. The logic behind random variables, expected value, and probability distributions explains everyday uncertainty, from weather forecasting to risk analysis. Understanding this connection helps you remember and apply formulas more intuitively.
Consider these examples:
- In business, probability is used to predict expected profits and long-term outcomes through the application of binomial distributions.
- In healthcare, geometric distributions model how many trials it takes before success (like treatment response).
- In quality control, probability helps estimate failure rates and detect production errors early.
The AP Statistics Unit 4 probability review builds this connection between theory and practice through scenario-based questions. UWorld’s lessons often use relatable contexts, such as drawing cards, manufacturing reliability, or rolling dice, to teach formulas with meaning. This real-world framing helps you reason through questions faster on test day because you’re not recalling equations, you’re understanding patterns. Once you grasp that randomness isn’t chaos but a measurable pattern, probability becomes logical and even enjoyable. That shift in perspective transforms how you study, and it’s one reason students who connect math to real life perform better across all AP Stats units.
How can I understand random variables in AP Stats Unit 4 more effectively?
Random variables are at the heart of AP Statistics Unit 4: Probability, Random Variables, and Probability Distributions. They describe uncertainty in a measurable form, transforming randomness into something that can be calculated and reasoned about. To understand them deeply, you must connect formulas with meaning. You can start by distinguishing between discrete and continuous random variables. Discrete variables count outcomes (like the number of heads), while continuous ones measure ranges (like height or time). Additionally, learn to calculate the expected value (the long-run average outcome) and variance (the degree of dispersion in results), and use visuals to visualize how probabilities distribute across possible values.
UWorld’s AP Stats Unit 4 probability review walks you through these ideas step-by-step using practical examples like dice rolls, manufacturing reliability, or investment outcomes. Each question builds intuition by showing how probability distributions predict real scenarios. When you understand why expected value equals the “average of all possible outcomes,” the formulas start to make sense intuitively. The more you link numbers to real meaning, the faster you’ll master this concept. By the time you reach inference units, random variables will feel like second nature—tools you can use to describe almost anything that involves uncertainty.
What strategies can help boost my overall AP Statistics Unit 4 exam score?
To raise your score in AP Statistics Unit 4: Probability, Random Variables, and Probability Distributions, you need a mix of strategy, structure, and mindset. The goal is not only to know the math but also to think like the test writer—predicting what they’re really asking for in each question.
Here’s a focused plan:
- Begin every session with 10–15 minutes of AP Stats probability review—focus on independence, conditional probability, and event rules.
- Alternate practice types: one day MCQs, the next day FRQs.
- Track recurring weaknesses—maybe binomial setups or random-variable definitions—and rewatch lesson segments addressing them.
- After every test, write short notes summarizing what confused you; that metacognitive step cements learning.
UWorld’s AP Statistics Unit 4 practice tests provide the repetition and feedback you need to close those gaps. Explanations go beyond formulas, showing how AP graders expect you to phrase reasoning. Reviewing these carefully helps you develop the clarity that top-scoring students show. Remember—Unit 4 underpins probability-based inference later, so mastering it now means smoother progress across the rest of the course. Build understanding, not speed; once logic clicks, speed follows naturally.
How does UWorld help me study smarter for AP Statistics Unit 4?
UWorld is built to make AP Statistics Unit 4 probability review interactive, logical, and focused on real exam thinking. Instead of overwhelming you with definitions, it teaches the “why” behind every rule and gives you constant feedback until the reasoning becomes second nature.
You’ll start by learning the basics, such as independence, conditional probability, and event relationships, through lessons that connect theory to relatable examples. Then, you’ll practice hundreds of AP Stats Unit 4 MCQs and FRQs that use the same logic and phrasing as the College Board exam. Each question includes full explanations for correct and incorrect options so you understand every decision.
UWorld’s analytics dashboard tracks how quickly and accurately you solve problems, helping you focus your time on weak topics, such as binomial or geometric distributions. The progress feels measurable, where each session shows where you’ve improved and what needs work. This smart feedback loop helps you study efficiently rather than endlessly. By the time you take your real exam, you’ll already think in the structured, logical way AP graders expect. With UWorld, studying becomes less about memorizing formulas and more about developing a mindset of mastering probability.
Are there downloadable or offline study materials for AP Statistics Unit 4?
Yes. You can access downloadable AP Statistics Unit 4 practice tests and study PDFs through UWorld and other trusted academic platforms. These offline resources are perfect for students who prefer print-based review sessions or want to practice without digital distractions.
Here’s how to make the most of them:
- Download full-length AP Stats Unit 4 probability review PDFs that include both MCQs and FRQs.
- Work through each set under timed conditions—mimic real testing environments.
- Annotate formulas, highlight tricky concepts, and summarize takeaways in your notes.
- Review your answers using UWorld’s detailed online explanations afterward.
Combining offline practice with digital review bridges both speed and understanding. Paper tests help with endurance and focus, while UWorld’s interactive tools explain the reasoning you can’t get from static answer keys. The AP Statistics Unit 4 study guide PDFs also make great quick references—you can revisit them anytime without logging in. Blending print and digital preparation ensures flexibility, keeps your routine varied, and reinforces memory through multiple learning modes. That balance—hands-on work plus guided reasoning—is the most effective way to master probability, random variables, and distributions before exam day.
Learn More About Specific Unit
Exploring One-Variable Data
Exploring Two-Variable Data
Collecting Data
Sampling Distributions
Inference for Categorical Data: Proportions
Inference for Quantitative Data: Means
Inference for Categorical Data: Chi-Square
Inference for Quantitative Data: Slopes