AP® Statistics Unit 2 Review and Practice Test
AP® Statistics Unit 2 prep doesn’t have to feel overwhelming! This AP Stats Unit 2 review simplifies two-variable data analysis with clear, step-by-step explanations, illustrative examples, and helpful visuals, making it easy to understand key concepts like correlation, regression lines, and outliers. Once you’ve mastered the concepts, reinforce your learning with AP Stats Unit 2 progress check MCQs and practice tests, designed to mirror real exam scenarios and build confidence for both multiple-choice and free-response questions.
Boost Your Confidence and Score High with Our AP Statistics Unit 2 Review
Ace AP® Statistics Unit 2 with confidence! This structured review combines clear lessons, engaging examples, and targeted practice with progress check MCQs and FRQs. Improve your problem-solving skills, identify areas to strengthen, and set yourself up for a high score on exam day.
Engaging Video Lessons
Make learning AP Statistics Unit 2 enjoyable and effective! Our interactive video lessons simplify complex topics like correlation coefficients and outliers, guiding you through each concept with visuals and real-world examples to reinforce understanding.
Interactive Study Guides
Study smarter with our AP Stats Unit 2 study guide. Concise notes, clear visuals, and targeted practice checkpoints turn every review session into measurable progress, helping you build confidence and prepare effectively for the AP exam.
Try These AP Statistics Unit 2 Practice Test Questions
Question
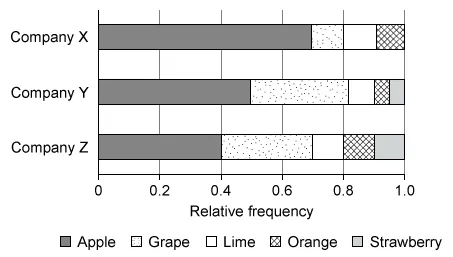
Candy companies X, Y, and Z make boxes of gummies in five fruit flavors. Anna bought a box from each company and determined the number of gummies of each flavor. The graph below shows the relative frequency distribution of flavors for each box of gummies.
Which of the following statements must be true?
| A. The number of lime gummies in the Company X box was equal to the sum of the number of lime gummies in the other two boxes. | |
| B. There were fewer grape gummies in the Company X box than in the Company Y box. | |
| C. There were more apple gummies than grape gummies in the Company Y box. | |
| D. There were more grape gummies than apple gummies in the Company Z box. | |
| E. There was the same number of lime gummies in the Company Y box as in the Company Z box. |
Hint:
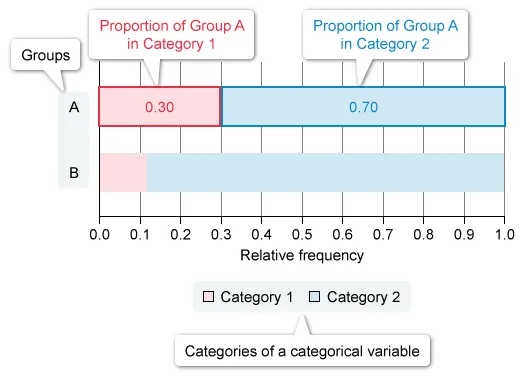
The width (or height) of segments in a segmented bar graph indicates either the relative frequency or counts of each category of a categorical variable.
Explanation
Each bar in a segmented bar graph represents a single group, and the width (or height) of the segments within each bar represents either the relative frequency or count of each category of a categorical variable in that group.
Note: A segmented bar graph of relative frequencies does not allow for a comparison of the number of observations per segment between groups unless the total number of observations in each group is given.
Analyze each answer choice to determine which of the statements is true, and recall that it is possible to compare only within the same box (because the total numbers of gummies in the boxes are not given).
Notice that in the Company Y box, the segment for apple gummies is larger than the segment for grape gummies.
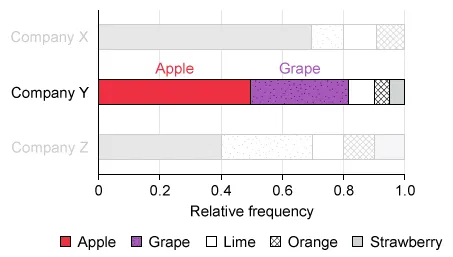
The relative frequency of apple gummies in the Company Y box is greater than grape gummies because the segment for apple gummies is longer than the segment for grape gummies (0.50 > 0.32).
Therefore, there were more apple gummies than grape gummies in the Company Y box.
(Choices A, B, and E) These statements are not true because the total number of gummies in each box is unknown and the given chart shows only relative frequencies (proportions). Therefore, it is impossible to compare the number of gummies of each flavor in different company boxes.
(Choice D) This statement is not true because the relative frequency of grape gummies in the Company Z box is approximately 0.3 and the relative frequency of apple gummies is 0.4.
Things to remember:
-
A segmented bar graph displays either the relative frequency or count distribution of a categorical variable in each of several groups.
-
A segmented bar graph of relative frequencies does not allow for a comparison of the number of observations per segment between groups unless the total number of observations in each group is given.
Question
For which of the following scatterplots is the correlation between x and y closest to 0 ?
A. 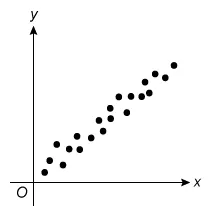 |
|
B. 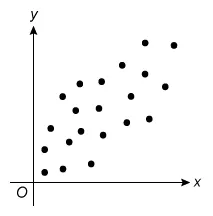 |
|
C. 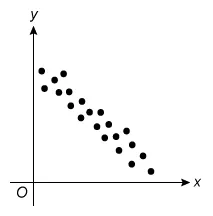 |
|
D.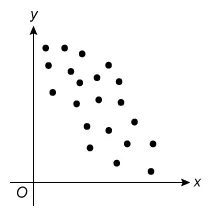
|
|
E. 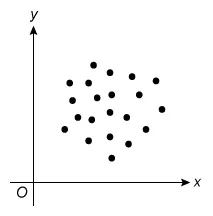
|
Hint:
The correlation coefficient describes the direction and strength of the relationship between two variables x and y.
Explanation
The correlation coefficient r describes the direction and strength of a linear relationship between two quantitative variables x and y. The magnitude of r indicates the strength of the relationship, and the sign of r indicates the direction.
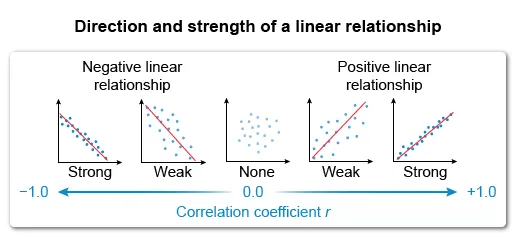
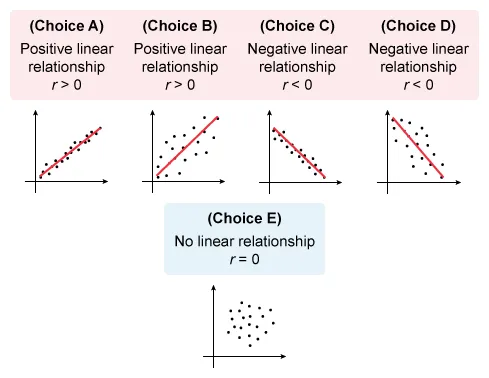
The question asks which scatterplot has a correlation closest to 0 (r = 0), which describes data with no linear relationship. Eliminate Choices A, B, C, and D because they show a linear relationship.
Of the choices, the scatterplot for which the correlation between x and y is closest to 0 is Choice E.
(Choices A and B)These scatterplots show different levels of strength of positive linear relationships (r > 0). However, the question asks for the plot with a correlation closest to 0 (r = 0).
(Choices C and D)These scatterplots show different levels of strength of negative linear relationships (r < 0). However, the question asks for the plot with a correlation closest to 0 (r = 0).
Things to remember:
- The correlation coefficient r describes the direction and strength of the relationship between two variables x and y.
- When two variables x and y do not show a linear relationship, the correlation coefficient r is equal to or close to 0.
Question
A pediatrician collected data on the age (in months) and length (in inches) of a random sample of boys between the ages of 1 and 12 months. A scatterplot of the data showed a strong linear relationship. The following regression was created:
length = 21.113 + 0.641(months)
The pediatrician uses the regression equation to predict the length of a 9-month-old boy and of an 18-month-old boy. Which of the following is a possible reason why the predicted length of the 9-month-old boy is more reliable than the predicted length of the 18-month-old boy?
| A. An age of 18 months is outside the interval of ages used to generate the regression equation. | |
| B. The age may not explain much of the variation in length. | |
| C. The correlation coefficient is positive. | |
| D. The slope of the sample regression line is greater than 0. | |
| D. The y-intercept of the sample regression is positive. |
Hint:
Extrapolation is the prediction of a response value for a value for the explanatory variable that is outside the interval of values used to determine the regression line.
Explanation
Extrapolation is the prediction of the value of the response variable y for a value for the explanatory variable x that is outside the interval of the x-values used to determine the regression line.
The predicted value is less reliable the further outside the x-values used to determine the regression line.
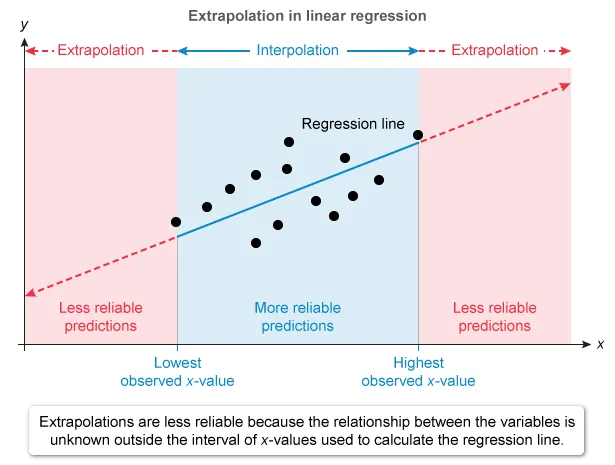
The regression predicts length (y) from the age (x) of boys aged 1 to 12 months, so the observed x-values range from 1 to 12 months. Unlike for a 9-month-old boy, the prediction for an 18-month-old is an extrapolation.
Therefore, the reason why the predicted length of the 9-month-old boy is more reliable than the predicted length of the 18-month-old boy is:
| An age of 18 months is outside the interval of ages used to generate the regression equation. |
(Choice B) The amount of variation in length explained by age describes how well the regression line fits the data, but it does not help to explain why a predicted value would be more precise than another.
(Choice C) A positive correlation coefficient indicates that as age increases, length tends to increase, but it does not help to explain why a predicted value would be more precise than another.
(Choices D and E) The slope and the y-intercept describe the regression line used to predict the length of boys from their age, but it does not help to explain why a predicted value would be more precise than another.
Things to remember:
-
Extrapolation is the prediction of the value of the response variable y for a value for the explanatory variable x that is outside the interval of x-values used to determine the regression line.
-
The predicted value is less reliable as an estimate the further the extrapolation.

Study Anywhere, Anytime
Tackle AP Statistics Unit 2 practice tests on the ride home from a game, review topic videos between classes, or dive into a study guide while waiting for friends at the coffee shop. Keep everything you need to ace the AP Statistics exam right at your fingertips. Get the app today!
Stand Out
with a Top Score on the AP Statistics Exam
Finish your AP Statistics Unit 2 review and continue mastering all units with UWorld. Complete our AP Statistics full review course to boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Stats Videos
- Print & Digital Study Guide
- 1300+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Statistics Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What is AP Statistics Unit 2 and why is it important for the exam?
AP Statistics Unit 2: Exploring Two-Variable Data introduces relationships between quantitative variables through graphical and numerical analysis. Students learn how to create and interpret scatterplots, measure the strength and direction of association, and use linear regression to model data. These concepts appear frequently in both AP Stats Unit 2 FRQ and MCQ sections, making this unit central to your statistical reasoning skills.
To study effectively:
- Review how correlation describes direction and strength.
- Understand how slope, intercept, and residuals describe model fit.
- Practice identifying outliers and influential points that affect regression lines.
These abilities help you explain real-world relationships using evidence, a key component of the AP Statistics exam.
UWorld’s AP Statistics Unit 2 review simplifies regression and correlation through step-by-step visuals and interactive problems that mirror College Board expectations, ensuring you learn both how to interpret and how to justify each conclusion.
Which topics are covered in AP Statistics Unit 2?
Unit 2 focuses on describing and analyzing relationships between two quantitative variables. Major topics include:
- Scatterplots and Association: Direction, form, and strength of relationships.
- Correlation (r): Calculating and interpreting values to describe linear strength.
- Least-Squares Regression Line: Finding slope, intercept, and making predictions.
- Residual Analysis: Evaluating model fit through pattern recognition.
- Outliers and Influential Points: Understanding their effect on regression.
These skills are emphasized in AP Stats Unit 2 MCQs and FRQs, where you explain or compute regression statistics in context.
Each topic builds toward quantitative reasoning used in later units on probability and inference. Students who master AP Statistics Unit 2 review concepts gain confidence in analyzing data trends and connecting numerical results with practical meaning.
How should I study for the AP Statistics Unit 2 review?
A strong AP Stats Unit 2 review balances concept learning, graph interpretation, and applied calculation. Start with correlation and gradually move to regression analysis.
Study plan:
- Week 1: Interpret scatterplots and describe associations.
- Week 2: Calculate r and understand its limitations.
- Week 3: Work on least-squares regression and residual plots.
- Final review: Connect concepts through mixed MCQs and FRQs.
Practice explaining slope and intercept in everyday language, this skill often distinguishes high-scoring responses. Visualizing patterns through graphs and data tables improves both accuracy and retention. UWorld’s AP Statistics Unit 2 practice test and study guide provide targeted regression and correlation exercises with detailed explanations, helping you move beyond memorization to analytical reasoning.
What’s the best study sequence for AP Stats Unit 2?
Following a clear sequence makes it easier to understand how relationships between variables are modeled and interpreted. A logical AP Stats Unit 2 review plan begins with conceptual visualization and ends with applied regression analysis.
Recommended order:
- Start with Scatterplots: Learn to describe direction, form, and strength.
- Move to Correlation (r): Interpret numerical strength and limitations.
- Progress to Least-Squares Regression: Derive slope, intercept, and predicted values.
- Analyze Residuals: Identify when models fit or fail.
- Finish with Outliers and Influential Points: Understand how they alter correlation and regression results.
This progression builds fluency for both AP Statistics Unit 2 FRQ and MCQ items, where you must explain association patterns in context. Mastering each step ensures a solid foundation before tackling later topics like sampling and inference.
What is the most effective AP Stats Unit 2 review plan before the exam?
Organize your AP Stats Unit 2 review into a 3-phase timeline to build consistency and depth.
3-Months Before the Exam:
- Review scatterplot interpretation and correlation basics.
- Watch short lessons on linear relationships and regression meaning.
- Attempt small data-set problems to practice describing direction and form.
1-Month Before the Exam:
- Practice calculating regression equations and interpreting r values.
- Solve one AP Statistics Unit 2 practice test weekly to test progress.
- Create formula summaries and slope/intercept interpretation notes.
2-Weeks Before the Exam:
- Work through mixed MCQs and FRQs involving real datasets.
- Review computer output interpretation and residual patterns.
- Focus on pacing and concise written explanations.
UWorld’s AP Statistics Unit 2 review integrates all three stages through visual modeling, adaptive practice, and data-driven analytics, helping you refine both accuracy and reasoning before exam day.
What are the main FRQ question types for AP Stats Unit 2?
The AP Statistics Unit 2 FRQ section evaluates your ability to analyze relationships between variables and interpret linear models in context. Common question types include:
- Interpretation Tasks: Explaining slope, intercept, and residual meaning.
- Model Evaluation: Using scatterplots and residuals to judge linear fit.
- Prediction Problems: Calculating and contextualizing predicted values.
- Outlier Analysis: Determining the effect of unusual data points.
- Comparative Scenarios: Describing how two relationships differ.
Each response must connect numerical reasoning to the scenario’s context. Practicing written explanations improves precision and clarity.
UWorld’s AP Stats Unit 2 FRQ-style practice questions offer guided solutions that model concise, exam-level explanations, a useful supplement to official samples.
How can I use UWorld’s AP Stats Unit 2 progress-check questions effectively?
UWorld’s AP Stats Unit 2 progress-check MCQs help you measure how well you understand correlation, regression, and residual interpretation after each topic. Treat these sets as short learning checkpoints rather than graded quizzes.
Best practices:
- Attempt a small set after completing a topic such as correlation or regression.
- Read every explanation fully to understand why an answer is correct.
- Note recurring patterns, like confusing slope interpretation or ignoring outliers.
- Re-attempt difficult questions after a few days to reinforce retention.
By focusing on reasoning instead of score, you’ll strengthen long-term understanding and be better prepared for the AP Statistics Unit 2 MCQ and FRQ sections.
How are correlation and regression concepts connected in AP Statistics Unit 2?
Correlation and regression describe the same relationship from two perspectives: correlation quantifies the strength and direction, while regression models the line that predicts one variable from another.
A strong positive correlation means as x increases, y tends to increase; a strong negative correlation shows the opposite. Regression uses this pattern to build an equation of best fit. However, correlation alone does not imply causation, context always matters.
Understanding this relationship is key to interpreting results in AP Stats Unit 2 FRQ problems. You might, for example, explain how slope relates to correlation or why residuals signal a poor linear fit. Visualizing both together improves analytical reasoning and data interpretation across the course.
How can I retain formulas and concepts from AP Stats Unit 2?
Retention improves when you connect visual understanding with repetitive recall. To remember Unit 2 equations and relationships:
- Make a quick-reference card with formulas for slope (b), intercept (a), correlation (r), and r².
- Use scatterplots to visualize what each value means.
- Teach the concept aloud, explaining slope or residuals strengthens memory.
- Practice predicting values manually before relying on a calculator.
Linking calculations to graphical reasoning ensures you remember not just numbers but also their meaning. UWorld’s interactive visuals and worked examples reinforce this link, showing how each formula translates into real-world relationships.
How do I study regression analysis for the Unit 2 test?
Studying regression and correlation effectively requires balancing computation, interpretation, and context.
Focus on:
- Understanding correlation strength (r) and direction through scatterplots.
- Learning least-squares regression steps: calculate, predict, and interpret.
- Interpreting residual plots to judge model fit.
- Practicing FRQs that connect slope and correlation to real-world meaning.
Alternate between untimed concept review and timed sets to improve accuracy and pacing.
UWorld’s AP Stats Unit 2 practice test questions mirror official exam patterns, letting you apply theory to data-driven scenarios while reviewing explanations that clarify both correct and incorrect reasoning.
What is the best AP Stats Unit 2 practice-test format?
An effective AP Statistics Unit 2 practice test should include both computation-based and interpretation-based questions to match the exam’s balance of reasoning and analysis.
Recommended format:
- 30–35 MCQs: Focus on correlation, regression, and residual interpretation.
- 2 FRQs: One that requires calculation and context explanation, another that analyzes model fit or outliers.
- Timing: 60–70 minutes total; review each missed question to identify whether the error was conceptual or procedural.
Simulating this structure develops both precision and pacing for the actual test.
UWorld’s AP Stats Unit 2 practice test provides customizable sets with immediate feedback, helping you evaluate progress and refine reasoning before exam day.
When should I begin preparing for the Unit 2 test?
Begin preparing for AP Stats Unit 2 as soon as regression and correlation are introduced in class. Early exposure builds familiarity with interpreting relationships between variables.
Recommended timeline:
- 3–4 weeks before the test: Review scatterplots, correlation basics, and practice describing associations.
- 2 weeks before: Work on regression analysis and residual interpretation.
- Final week: Focus on mixed MCQs and FRQs that require explanation of patterns and model evaluation.
Consistent, short sessions (20–30 minutes daily) reinforce understanding better than long, infrequent reviews. Regularly revisit Unit 1 concepts, as describing shape, center, and spread supports clearer interpretation of two-variable data.
What are common mistakes students make in AP Stats Unit 2?
Students often lose points in AP Statistics Unit 2 FRQ and MCQ sections because of subtle misinterpretations.
Common pitfalls include:
- Confusing correlation strength with causation.
- Misreading residual plots or ignoring nonlinear patterns.
- Forgetting to interpret slope and intercept in context.
- Overlooking the influence of outliers or high-leverage points.
Precision matters, each explanation should connect statistical calculation to the scenario.
UWorld’s diagnostic insights help identify recurring mistakes through question-by-question feedback. Reviewing these patterns sharpens your statistical reasoning and ensures greater accuracy under exam pressure.
Where can I find AP Statistics Unit 2 notes, cheat sheets, or study guides?
Reliable AP Stats Unit 2 study guides and notes summarize essential ideas like correlation, regression, and residual interpretation. Look for resources that include:
- Step-by-step examples of linear modeling.
- Visual aids explaining slope and intercept meaning.
- Sample scatterplots with outlier annotations.
- Quick reminders about causation versus association.
Concise cheat sheets are best for last-minute review, while full study guides help build conceptual depth. Combining both ensures balanced preparation for tests and progress checks.
Are there downloadable AP Statistics Unit 2 study-guide PDFs and practice materials?
Yes. Downloadable AP Statistics Unit 2 review PDFs and worksheets offer condensed summaries of equations, definitions, and regression examples. Choose resources aligned with the College Board’s Course and Exam Description for consistency.
UWorld provides printable and digital AP Stats Unit 2 study guides, flashcards, and interactive question sets that strengthen understanding of scatterplots, correlation, and regression analysis. Combining these with official materials ensures both conceptual mastery and exam-style readiness for Exploring Two-Variable Data.
Learn More About Specific Unit
Exploring One-Variable Data
Collecting Data
Probability, Random Variables, and Probability Distributions
Sampling Distributions
Inference for Categorical Data: Proportions
Inference for Quantitative Data: Means
Inference for Categorical Data: Chi-Square
Inference for Quantitative Data: Slopes