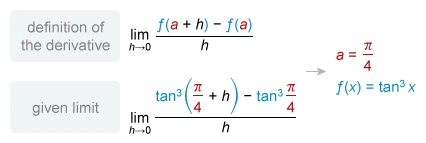AP® Calculus BC Unit 3 Review and Practice Test
Sharpen your understanding of derivatives with this AP® Calculus BC Unit 3 review. Explore composite, implicit, and inverse differentiation through clear explanations and examples designed to build confidence before your upcoming Unit 3 test and AP exam.
Master Every Concept with Our AP Calculus BC Unit 3 Review
Prepare for your AP Calc BC Unit 3 test with clear lessons on composite, implicit, and inverse differentiation. This AP Calculus BC Unit 3 review helps you understand key formulas, avoid common errors, and build confidence for the exam.
Engaging Video Lessons
Learn AP Calculus BC Unit 3 concepts through step-by-step video lessons that simplify complex ideas. Each AP Calc BC Unit 3 review video breaks down composite, implicit, and inverse differentiation with examples. Strengthen your understanding before taking the AP Calculus BC Unit 3 progress check MCQ or test.
Interactive Study Guides
Reinforce your learning with AP Calculus BC Unit 3 interactive study guides that make differentiation easier to grasp. These AP Calc BC Unit 3 review materials include summaries, solved examples, and quick tips. Use them to prepare efficiently for your Unit 3 AP Calc BC test and progress check MCQs.
Sharpen Your Skills with AP Calculus BC Unit 3 Practice Questions
Question
If
| A. | |
| B. | |
| C. | |
| D. |
Hint :
To differentiate a composite function, use the chain rule.
Explanation
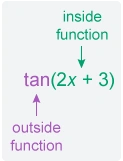
The given function is a composite function of the form where u=tan(2x+3) is the inside function.
To find the derivative of a composite function of this form use the chain rule:
First differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x .
| Given function | |
| Apply the chain rule: |
To differentiate , notice that it is also a composite function. The function is of the form tan u , where is the inside function.
Apply the chain rule again to determine
Differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x .
| Derivative of | |
| Apply: | |
| Differentiate: | |
| Rearrange factors |
Substitute into the equation for
| Equation for | |
| Substitute: | |
| Simplify |
The derivative is equal to 4tan(2x + 3)sec2(2x + 3).
(Choice A) may be a result of incorrectly applying the chain rule to differentiate :
(Choice B) may be a result of incorrectly applying the chain rule to differentiate : .
(Choice C) may be a result of neglecting to use the chain rule when differentiating : .
Things to remember:
To differentiate a composite function where u is the inside function, use the chain rule:
Question
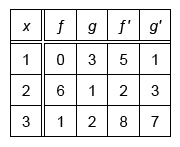
The table above gives selected values of two differentiable functions f and g along with their derivatives. If y = f(g(x)), what is the value of at x = 2 ?
| A. 3 | |
| B. 6 | |
| C. 8 | |
| D. 15 |
Explanation
To find at x = 2, differentiate f(g(x)) with the chain rule and plug in x = 2. Use values given in the table to evaluate.
| Derivative of given function | |
| Apply chain rule | |
| Plug in x = 2 | |
| Plug in g(2) = 1 and g′(2) = 3 from given table | |
| Plug in f ′(1) = 5 from given table | |
| Multiply |
Therefore, at x = 2 is 15.
Question
| A. 3 | |
| B. | |
| C. 6 | |
| D. 12 |
Explanation
The given limit is in a form of the limit definition of the derivative, so compare it to the limit definition of the derivative and identify the function f(x) and the x-value.
Therefore, the limit represents the derivative of the function tan3 x at .
The function tan3 x = (tan x)3 is a composite function of the form u3, where u = tan x is the inside function, so differentiate with the chain rule.
| Function in given limit | |
| Differentiate | |
| Apply chain and power rules | |
| Apply tangent differentiation rule |
The derivative of tan3 x is 3 tan2 x sec2 x. Now plug in to find the value of the given limit.
| Resulting derivative | |
| Plug in | |
| Plug in and | |
| Simplify |
Therefore, .
Stand Out
with a Top Score on the AP Calculus BC Exam
Wrap up your AP Calculus BC Unit 3 review and keep advancing through later units with UWorld. Boost your performance and stand out as a top candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc BC Videos
- Print & Digital Study Guide
- 1800+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What are the main topics covered in AP Calculus BC Unit 3?
Differentiation: Composite, Implicit, and Inverse Functions?
AP Calculus BC Unit 3 dives into advanced differentiation techniques that extend beyond basic derivative rules. You’ll learn to handle more complex relationships between functions and apply them in both pure and applied math contexts.
- The chain rule for differentiating composite functions: Learn how to find derivatives when one function is nested within another, a skill essential for tackling multi-step differentiation problems.
- Implicit differentiation: Understand how to differentiate equations where y isn’t isolated, a vital concept for related rates and curve analysis.
- Differentiation of general and particular inverse functions: Master finding derivatives of inverse trigonometric, exponential, and logarithmic functions with precision.
- Determining higher-order derivatives of functions: Explore how to compute second and third derivatives to analyze motion, concavity, and rates of change.
These skills form the foundation of your AP Calc BC Unit 3 review and appear frequently in the Unit 3 progress check MCQ and AP Calculus BC Unit 3 test.
How should I prepare for an AP Calculus BC Unit 3 exam?
Preparing for the AP Calculus BC Unit 3 exam requires a structured plan that combines reading, watching, and practicing. Unit 3 covers composite, implicit, and inverse differentiation, so consistent exposure to examples and applications is key to building confidence.
- Read: Begin with concise notes or a study guide for AP Calc BC Unit 3 that explains the chain rule, implicit differentiation, and higher-order derivatives. Focus on understanding formulas rather than memorizing them. Review worked examples and pay attention to common errors highlighted in your textbook or reliable online resources.
- Watch: Use AP Calculus BC Unit 3 review videos to see differentiation techniques in action. Visual explanations help clarify how each rule connects and when to apply it. Pause and rewatch tough examples to fully grasp the logic behind each step.
- Practice: Reinforce what you learn by attempting AP Calc BC Unit 3 test questions and progress check MCQs. With UWorld’s AP Calculus BC Unit 3 practice, you’ll access step-by-step solutions, instant feedback, and detailed performance analytics—helping you turn every mistake into progress and feel fully prepared for exam day.
Are any free resources available for AP Calculus BC Unit 3?
For complete exam readiness, try UWorld’s AP Calc BC Unit 3 review, which offers a free trial so you can experience its detailed, exam-style questions. UWorld goes beyond basic practice; each problem includes in-depth explanations, visual solutions, and performance tracking to help you prepare efficiently.
Yes, several free resources can help you get started with your AP Calculus BC Unit 3 review and strengthen your understanding of differentiation. Begin with College Board’s AP Classroom, which offers Unit 3 progress check MCQs and sample FRQs aligned with official exam standards. These questions are great for identifying areas that need extra attention.
You can also explore Khan Academy’s AP Calculus BC Unit 3 lessons, which break down composite, implicit, and inverse differentiation topics into short, clear video tutorials. The platform provides step-by-step explanations and guided practice, making it useful for reinforcing the basics before tackling harder problems.
What types of questions are on the AP Calculus BC Unit 3 test?
The AP Calculus BC Unit 3 test evaluates how well you understand and apply advanced differentiation techniques. You’ll encounter both multiple-choice questions (MCQs) and free-response questions (FRQs) that require reasoning, algebraic manipulation, and conceptual understanding.
Question types you can expect include:
- Symbolic differentiation: Problems that test your ability to apply the chain rule and find higher-order derivatives accurately.
- Graphical interpretation: Tasks involving slopes, tangent lines, or concavity derived from given graphs.
- Applied scenarios: FRQs using implicit and inverse differentiation in real-world contexts, such as physics or economics.
The Unit 3 progress check MCQ from College Board is a great benchmark, but to build true exam readiness, consistent targeted practice is key. With UWorld’s AP Calculus BC Unit 3 review, you get realistic, exam-level questions modeled after the actual AP test.
How can I improve my score on the Free-Response Questions (FRQs) for Unit 3?
Improving your FRQ performance for AP Calculus BC Unit 3 requires strategy, clarity, and consistent practice. FRQs test not only your ability to find correct derivatives but also your reasoning process. The best way to prepare is to focus on understanding why each differentiation step works, rather than memorizing formulas.
Start by reviewing the main Unit 3 concepts: composite, implicit, and inverse differentiation, and make sure you can explain each rule in your own words. Practice showing every logical step clearly, since the AP grader awards points for correct reasoning and setup, even if the final answer isn’t perfect.
Here’s a simple plan to boost your score:
- Review one FRQ daily, focusing on differentiation-based prompts.
- Write out full solutions, including explanations and justifications.
- Compare your work with official AP Calc BC Unit 3 review examples or progress check MCQs.
For guided improvement, use UWorld’s AP Calculus BC Unit 3 practice questions. Each FRQ-style problem includes detailed explanations, visual walkthroughs, and grading insights aligned with AP standards.
What is the "Differentiation: Composite, Implicit, and Inverse Functions" unit's weight on the AP Calculus BC exam?
The AP Calculus BC Unit 3: Differentiation—Composite, Implicit, and Inverse Functions is one of the most important sections of the course, typically accounting for about 4-7% of the total AP Calculus BC exam. This unit bridges foundational derivative rules from earlier lessons with more advanced concepts that appear frequently in both multiple-choice questions (MCQs) and free-response questions (FRQs).
Because Unit 3 integrates multiple differentiation methods, you can expect it to appear across several types of problems—symbolic, graphical, and application-based. Questions may require using the chain rule, performing implicit differentiation, or finding derivatives of inverse functions such as logarithmic or trigonometric relationships. Strong performance here often leads to higher overall exam scores since these skills reappear in later units involving motion, accumulation, and series.
To prepare effectively, focus on practicing each topic systematically using a reliable AP Calculus BC Unit 3 review resource. While College Board’s progress check MCQs provide insight into question style, UWorld’s AP Calc BC Unit 3 practice questions go a step further. With detailed, step-by-step explanations and real exam-style problems, UWorld’s AP Calculus BC Unit 3 review helps you build accuracy, confidence, and test-day readiness.
Where can I find a good study guide for AP Calculus BC Unit 3?
UWorld’s AP Calculus BC Unit 3 review and practice questions are the best place to start if you’re looking for a reliable study guide. UWorld offers a structured learning path that combines in-depth explanations, visual solutions, and question-level feedback to strengthen your understanding of differentiation topics such as the chain rule, implicit differentiation, and derivatives of inverse functions. Whether you’re preparing for the AP Calculus BC Unit 3 test or revising for your final exam, UWorld’s comprehensive study guide and free trial give you the edge you need to master the unit.
You can also refer to trusted academic resources and classroom materials that summarize formulas, include solved examples, and highlight common errors students make in this unit. Websites like Khan Academy offer concise AP Calc BC Unit 3 review notes with topic explanations and quick quizzes to help you refresh your memory and build conceptual clarity. The College Board’s AP Classroom provides Unit 3 progress check MCQs and FRQs that closely match the real exam format, making them excellent tools for self-assessment.
Can I find practice tests specifically for AP Calc BC Unit 3?
Yes, there are several targeted practice tests for AP Calculus BC Unit 3 that focus on advanced differentiation concepts like the chain rule, implicit differentiation, and derivatives of inverse functions. These tests simulate the question styles you’ll encounter on both the multiple-choice (MCQ) and free-response (FRQ) sections of the exam, allowing you to assess your readiness for the AP Calc BC Unit 3 test.
To make the most of these practice tests:
- Choose tests labeled specifically for Unit 3 to ensure they cover composite, implicit, and inverse differentiation.
- Time yourself to build speed and accuracy while solving problems similar to those on the real exam.
- Review your incorrect answers carefully to understand the reasoning behind each solution and strengthen weak areas.
While several online resources offer general calculus practice, UWorld’s AP Calculus BC Unit 3 review provides the most exam-like experience. You can even start with a free trial to explore thousands of AP Calc BC Unit 3 practice questions with detailed, step-by-step solutions. UWorld’s analytics help track your progress, highlight improvement areas, and give you the confidence to perform your best on both the Unit 3 progress check MCQ and the actual AP Calculus BC Unit 3 exam.
What are the best online calculators or graphing tools for verifying Unit 3 problems in AP Calc BC?
When studying AP Calculus BC Unit 3, reliable graphing tools help you verify answers and visualize key concepts like composite, implicit, and inverse differentiation. The College Board–approved graphing calculator and the built-in Desmos graphing calculator through Bluebook are your best options for AP Calc BC practice. These tools replicate the digital testing environment and let you check derivatives, tangent lines, and function behaviors efficiently.
To make your preparation even stronger, try UWorld’s AP Calc BC Unit 3 practice tests and study guides. UWorld offers realistic exam-style questions, step-by-step solutions, and visual learning aids that mirror real AP exam scenarios. Sign up for a free UWorld trial to boost your confidence and master differentiation for test day success.
Why is AP Calculus BC Unit 3 important for the AP exam?
AP Calculus BC Unit 3 is a core building block for the entire course. It develops your ability to handle complex differentiation, which is essential for solving advanced problems in later units like Applications of Derivatives and Differential Equations. Many multiple-choice and FRQ questions on the AP Calculus BC exam directly test concepts from this unit, such as implicit and inverse differentiation. Part A of the exam does not allow a graphing calculator, while Part B requires one for select questions involving complex computations or graph-based reasoning.
Mastering Unit 3 ensures you can move confidently through higher-level calculus problems and apply these rules under timed conditions. With UWorld’s AP Calculus BC Unit 3 review and practice questions, you’ll gain a clear understanding of how these concepts appear on the test and strengthen the reasoning skills needed for top scores.
How much time should I spend studying AP Calculus BC Unit 3?
It’s best to dedicate at least one week to studying AP Calc BC Unit 3 thoroughly. Break your sessions into smaller blocks: spend time reading lessons, solving practice problems, and reviewing errors. Try to cover one topic: composite, implicit, or inverse differentiation per session to avoid information overload.
Consistency is key. A mix of short daily reviews and practice tests leads to stronger retention than last-minute cramming. With UWorld’s AP Calculus BC Unit 3 study guides and timed practice questions, you can follow a structured study plan, monitor progress, and build confidence before exam day, all accessible on the UWorld app anytime, anywhere.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Differential Equations
Applications of Integration
Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Infinite Sequences and Series