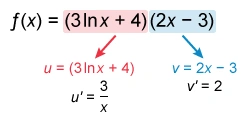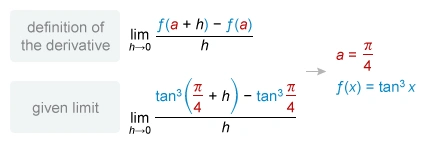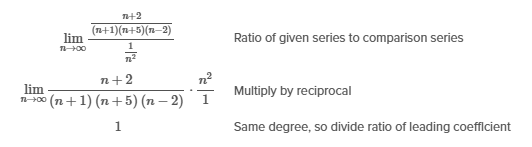AP® Calculus BC Practice Tests & Questions
Prepare for the AP® Calculus BC exam with 1,800+ multiple-choice questions and realistic FRQs* created by expert AP educators. Build unlimited quick quizzes or targeted practice tests on any topic.
Forget boring answer keys. Get crystal-clear explanations, eye-catching visuals, and real-time progress insights that show you exactly what to work on. Study with purpose, master every concept, and crush the exam.
Try Free AP Calculus BC Practice Test Questions
AP Calculus BC Practice Test: Limits and Continuity
Question
The table above gives values of a function f at selected values of x. Which of the following limits appear to exist?
| A. | |
| B. | |
| C. | |
| D. All the Above |
Explanation
As values of x get very close to 1 from the left, values of f get very close to 2. Therefore,
As values of x get very close to 1 from the right, values of f get very close to 2. Therefore,
Both one-sided limits of f equal 2 as x approaches 1. Therefore, it is reasonable to assume the two-sided limit exists and approximately equals 2.
Question
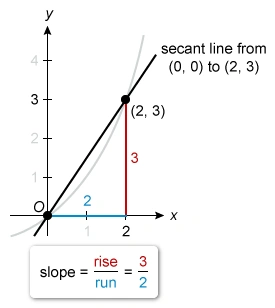
The graph of a function f is shown above. What is the average rate of change in f over the interval [0, 2] ?
Question
| A. -1 | |
| B. 0 | |
| C. 1 | |
| D. The limit does not exist. |
Explanation
First note that direct substitution yields an indeterminate form, Use the definition of tan x to rewrite the expression with as a factor and evaluate.
Therefore, the given limit equals 1.
AP Calculus BC Practice Test: Differentiation: Definition and Fundamental Properties
Question
If f(x) = (3lnx + 4)(2x − 3), then f′(x) =
| A. | |
| B. | |
| C. | |
| D. |
Hint :
To find the derivative of the product of two functions, use the product rule.
Explanation
To find the derivative of the product of two functions, use the product rule:
First identify u and v from the given function f(x) = (3lnx + 4)(2x − 3), and then differentiate to determine u′ and v′.
(Choice A) may result from incorrectly calculating the derivative of the product as u′v′ instead of uv′ + vu′.
(Choice B) may result from incorrectly calculating the derivative of the product as u′ + v′ instead of uv′ + vu′.
(Choice D) may result from incorrectly calculating the derivative of the product as uu′ + vv′ instead of uv′ + vu′.
Things to remember:
To find the derivative of the product of two functions, use the product rule:
Question
If a function f is not differentiable at x = −2, which of the following statements must be true?
| A. f′(−2) = 0 | |
| B. f(−2) does not exist | |
| C.
does not exist |
|
| D.
does not exist |
Hint :
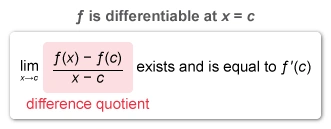
A function is differentiable at x = c only if its derivative at x = c exists.
Explanation
A function f is differentiable at x = c only if the derivative of f at x = c exists. If the derivative exists, then the limit of the difference quotient at x = c exists and is equal to the derivative.
Note: The limit of the difference quotient can also be expressed as
If f is not differentiable at x = −2, the derivative at x = −2 does not exist. Therefore, does not exist.
(Choice A) "f′(−2) = 0" may result from the misconception that if a function is not differentiable at a point, then its derivative is zero at that point instead of nonexistent.
(Choice B) "f(−2) does not exist" may result from assuming that if a function is not differentiable at a point, then the function does not exist at that point.
(Choice C) "does not exist" may result from mistaking the limit of f as x approaches −2 with the limit of the difference quotient as x approaches −2.
Things to remember:
A function f is differentiable at x = c if the derivative of f at x = c exists. If the derivative exists, the limit of the difference quotient
exists and is equal to the derivative f′(c).
Question
The oil temperature in a car's engine is modeled by T, where T(t) is the temperature in degrees Fahrenheit, and t is the time, in minutes, after the engine is started. Which of the following indicates that the oil is getting hotter 12 minutes after the engine is started?
| A. T(12) < 0 | |
| B. T(12) > 0 | |
| C. | |
| D. |
Hint :
The sign of the derivative of a function indicates whether the function is increasing or decreasing.
Explanation
The function T gives the temperature of the oil in the car's engine, so the derivative of T gives the instantaneous rate of change in the temperature of the oil.
The sign of T′ indicates whether the temperature T of the oil is increasing or decreasing. If the values of the function's derivative T′ are positive, then the values of T are increasing.
If the oil is getting hotter 12 minutes after the engine is started (at t = 0), the temperature of the oil is increasing at t = 12. Therefore, the derivative of T is positive at that time:
(Choice A) T(12) < 0 indicates that the temperature of the oil is negative at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
(Choice B) T(12) > 0 indicates that the temperature of the oil is positive at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
(Choice C) indicates that the temperature of the oil is getting cooler at t = 12, but the question asks for the statement that indicates the temperature of the oil is getting hotter.
Things to remember:
- The notation gives the derivative of a function y with respect to x.
- If the derivative of a function is positive, then y is increasing. If is negative, then y is decreasing.
AP Calculus BC Practice Test: Differentiation: Composite, Implicit, and Inverse Functions
Question
If
| A. | |
| B. | |
| C. | |
| D. |
Hint :
To differentiate a composite function, use the chain rule.
Explanation
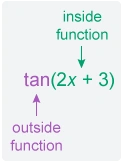
The given function is a composite function of the form where u=tan(2x+3) is the inside function.
To find the derivative of a composite function of this form use the chain rule:
First differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x .
| Given function | |
| Apply the chain rule: |
To differentiate , notice that it is also a composite function. The function is of the form tan u , where is the inside function.
Apply the chain rule again to determine
Differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x .
| Derivative of | |
| Apply: | |
| Differentiate: | |
| Rearrange factors |
Substitute into the equation for
| Equation for | |
| Substitute: | |
| Simplify |
The derivative is equal to 4tan(2x + 3)sec2(2x + 3).
(Choice A) may be a result of incorrectly applying the chain rule to differentiate :
(Choice B) may be a result of incorrectly applying the chain rule to differentiate : .
(Choice C) may be a result of neglecting to use the chain rule when differentiating : .
Things to remember:
To differentiate a composite function where u is the inside function, use the chain rule:
Question
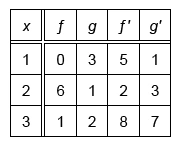
The table above gives selected values of two differentiable functions f and g along with their derivatives. If y = f(g(x)), what is the value of at x = 2
| A. 3 | |
| B. 6 | |
| C. 8 | |
| D. 15 |
Explanation
To find at x = 2, differentiate f(g(x)) with the chain rule and plug in x = 2. Use values given in the table to evaluate.
| Derivative of given function | |
| Apply chain rule | |
| Plug in x = 2 | |
| Plug in g(2) = 1 and g′(2) = 3 from given table | |
| Plug in f ′(1) = 5 from given table | |
| Multiply |
Therefore, at x = 2 is 15.
Question
| A. 3 | |
| B. | |
| C. 6 | |
| D. 12 |
Explanation
The given limit is in a form of the limit definition of the derivative, so compare it to the limit definition of the derivative and identify the function f(x) and the x-value.
Therefore, the limit represents the derivative of the function tan3 x at .
The function tan3 x = (tan x)3 is a composite function of the form u3, where u = tan x is the inside function, so differentiate with the chain rule.
| Function in given limit | |
| Differentiate | |
| Apply chain and power rules | |
| Apply tangent differentiation rule |
The derivative of tan3 x is 3 tan2 x sec2 x. Now plug in to find the value of the given limit.
| Resulting derivative | |
| Plug in | |
| Plug in and | |
| Simplify |
Therefore, .
AP Calculus BC Practice Test: Contextual Applications of Differentiation
Question
A particle is moving along the x -axis with position given by At what time t in the interval is the particle's instantaneous velocity equal to its average velocity over the interval ?
| A. 0 | |
| B. | |
| C. | |
| D. 9 |
Hint :
The Mean Value Theorem guarantees the existence of at least one value of x=c in the closed interval [a,b] for which the instantaneous rate of change of a continuous and differentiable function f(x) equals the average rate of change of f on [a,b] .
Explanation
The velocity v(t) of a moving particle is given by the derivative of the particle's position function x(t) .
Since velocity is the derivative of position, the instantaneous velocity is the instantaneous rate of change of the position x . Similarly, the average velocity is the average rate of change (AROC) of the position x .
The Mean Value Theorem (MVT) guarantees that there exists at least one value of x in the closed interval [a,b] for which the instantaneous rate of change (IROC) of a continuous and differentiable function f(x) equals the average rate of change (AROC) of f on [a,b] .
To determine the value of t = c for which the instantaneous velocity equals the average velocity of the particle on the given interval, first differentiate the position function to find an equation for the instantaneous velocity to find an equation for the instantaneous velocity .
| Given position function | |
| Rewrite | |
| Differentiate: | |
| Simplify and rewrite and |
To calculate the average velocity of on , use the formula for average rate of change with the given function x:
| AROC formula | |
| Plug in a = 0 and b = 9 | |
| Evaluate for t = 0 and t = 9 | |
| Take the square root of 9 and 0 | |
| Simplify |
Now set the expression for the instantaneous velocity equal to the average velocity and solve for t.
| Set the instantaneous velocity = average velocity | |
| Substitute and | |
| Cross multiply | |
| Divide both sides by 2 | |
| Square both sides |
Therefore, the value of t in the interval 0 ≤ t ≤ 9 for which the particle's instantaneous velocity equals its average velocity is
(Choices A and D) 0 and 9 may result from the assumption that the particle's instantaneous velocity and average velocity are equal at one of the endpoints.
(Choice B) may result from setting the given position function x(t) , instead of the instantaneous velocity function x′(t) , equal to the average velocity.
Things to remember:
- The velocity of a moving particle is given by the derivative of the particle's position function. .
- The conclusion of the Mean Value Theorem guarantees the existence of at least one value x=c in the open interval (a,b) at which the instantaneous rate of change of a continuous function f(x) is equal to the average rate of change of f on the interval [a,b]
Question
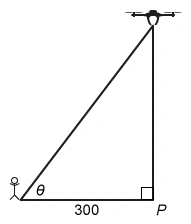
A person stands 300 feet from point P and watches a drone rise vertically from the point, as shown in the figure above. The drone is rising at a constant rate of 50 feet per second. What is the rate of change, in radians per second, of angle θ at the instant when the drone is 400 feet above point P ?
| A. | |
| B. | |
| C. | |
| D.
|
Hint :
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Explanation
To find a quantity when given the rates at which multiple variables are changing (related rates), first identify the quantity to be found, when it is to be found, and any other given values or rates.
The question asks for the rate of change in the angleθ when the drone's height h is 400 feet above point P. It is given that the person is 300 feet from point P, and the drone rises at a constant rate of feet per second.
A trigonometric equation for a right triangle that relates an acute angle θ of a right triangle to the lengths of the adjacent side b and opposite side h is
The angle θ and the length of the opposite side h are changing, but the adjacent side b remains constant. Plug the constant value b = 300 into the equation, differentiate with respect to time t,and solve for
| Equation for tangent of θ | |
| Plug in b = 300 | |
| Differentiate with respect to t | |
| Apply definition of secant | |
| Multiply both sides by cos 2θ |
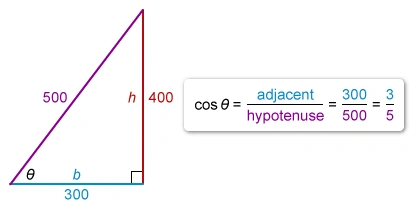
The values of b and are given, and the trigonometric ratio for cos θ is However, the hypotenuse of the right triangle (the distance between the person and the drone) is unknown.
The height of the drone (400 feet) and the person's distance from point P (300 feet) correspond to a 3-4-5 Pythagorean triple, so the hypotenuse of the right triangle is 500 feet.
To find , substitute the values of b, , and cos θ into the equation for .
| Equation for with cos2 θ rewritten as (cos θ)2 | |
| Substitute values | |
| Simplify | |
| Multiply |
The rate of change of angle θ with respect to time t is radians per second.
(Choice B) may result from incorrectly differentiating tan θ as sec θ tan θ, instead of sec² θ.
(Choice C) may result from incorrectly differentiating tan θ as sin θ, instead of sec2 θ.
(Choice D) may result from incorrectly differentiating tan θ as cos² θ, instead of sec2 θ.
Things to remember:
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Question
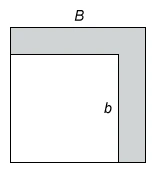
A region is bounded by two squares that have a common vertex at the bottom-left corner, as shown in the shaded region in the figure above. The side length of the outer square, B, is increasing at a constant rate of 3 meters per second, and the side length of the inner square, b, is decreasing at a constant rate of 1 meter per second. What is the rate of change, in square meters per second, of the area of the region at the instant when B is 5 meters and b is 4 meters?
| A. 4 | |
| B. 8 | |
| C. 22 | |
| D. 38 |
Hint :
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
Explanation
To find a quantity when given the rates at which multiple variables are changing (related rates), first identify the quantity to be found, when it is to be found, and any other given values or rates.
The question asks for the rate of change in the shaded area when the side lengths B and b are 5 and 4 meters, respectively. Side length B is increasing and b is decreasing, so and meters per second.
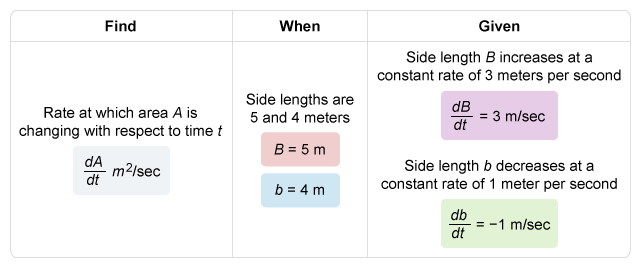
The area of the shaded region is given by the difference between the areas of the two squares. A square with side length s has area A = s2, so the shaded region has area A = B2 − b2.
Now differentiate both sides of the equation with respect to t, plug in the given side lengths and rates of change, and evaluate
| Area of shaded region | |
| Differentiate with respect to t | |
| Plug in given values | |
| Simplify |
Therefore, the rate of change in the area of the shaded region at the given instant is 38 square meters per second.
(Choice A) 4 may result from the error described in Choice B and not including the constant multiple 2 when applying the power rule to differentiate (B − b)².
(Choice B) 8 may result from incorrectly using A = (B − b)² as the formula for the area of the shaded region, instead of A = B² − b².
(Choice C) 22 may result from incorrectly using as the rate of change for the smaller side length. The side length is decreasing, so the rate of change is negative.
Things to remember:
To find a quantity when given the rates at which multiple variables are changing, first identify the quantity to be found, when it is to be found, and any other given values or rates.
AP Calculus BC Practice Test: Analytical Applications of Differentiation
Question
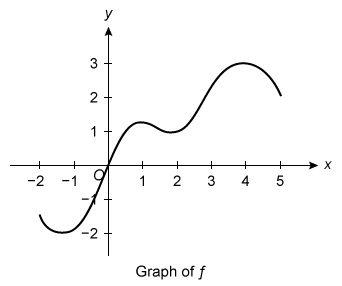
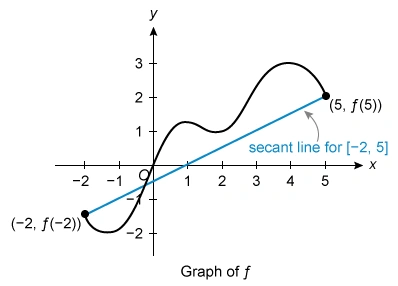
The graph of a differentiable function is shown on the closed interval . How many values of x in the open interval satisfy the conclusion of the Mean Value Theorem for ?
| A. One | |
| B. Two | |
| C. Three | |
| D. Four |
Hint :
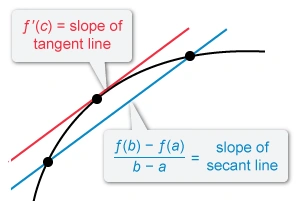
The Mean Value Theorem guarantees the existence of at least one value of in the open interval at which the slope of the line tangent to the graph of equals the slope of the secant line on .
Explanation
The Mean Value Theorem (MVT) guarantees the existence of at least one value in the open interval at which the slope of the line tangent to the graph of equals the slope of the secant line on .
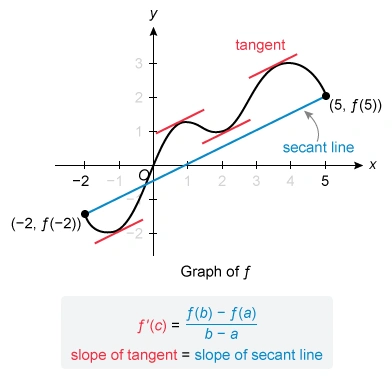
To determine how many values of x in the open interval satisfy the conclusion of the Mean Value Theorem, first connect the endpoints of the graph to draw the secant line.
Now count the number of times that a tangent line drawn to the curve is parallel to the secant line. Parallel lines have the same slope, so the slope of each tangent line must be equal to the slope of the secant line.
Note: It is not necessary to determine the exact values of the points of tangency.
Therefore, there are four values of x in the open interval (−2, 5) that satisfy the conclusion of the Mean Value Theorem for [−2, 5].
(Choice A) "One" may be a result of mistakenly assuming that there can only be one possible value of x that satisfies the conclusion of the Mean Value Theorem.
(Choices B and C) "Two" and "Three" may be a result of neglecting to include all the values of x where the tangent to the graph is parallel to the secant line.
Things to remember:
The Mean Value Theorem guarantees the existence of at least one value
in the open interval
at which the slope of the line tangent to the graph of
equals the slope of the secant line on .
Question
If f(x) = x sin x, which of the following does the second derivative test guarantee about the function f at x = 0 ?
| A. The function f has a relative minimum at x = 0. | |
| B. The function f has a relative maximum at x = 0. | |
| C. The second derivative test is inconclusive for the function f at x = 0. | |
| D. The function f does not meet the conditions of the second derivative test at x = 0, so the test cannot be applied. |
Explanation
The second derivative test can be applied to a function f at any x = c for which f′′(c) exists and f′(c) = 0.
To determine if the second derivative test can be applied to the given function at x = 0, first calculate f′(0). The given function is a product of functions, so differentiate with the product rule.


The second derivative is positive, so the second derivative test states that f has a relative minimum at x = 0.
Question
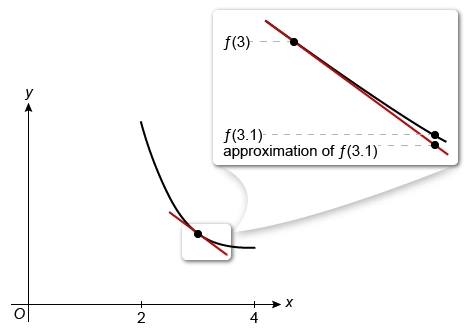
A function f is decreasing and concave up on the interval [2, 4]. Which inequality gives the following values in increasing order?
I. f(3)
II. f(3.1)
III. The approximation of f(3.1) using the line tangent to f at x = 3
| A. I < II < III | |
| B. II < III < I | |
| C. III < I < II | |
| D. III < II< I |
Explanation
The function f is decreasing, so f(3.1) < f(3). The function f is concave up, so tangent line approximations underestimate values near the point of tangency. Therefore, the approximation of f(3.1) using the line tangent to f at x = 3 must be less than f(3.1).
Therefore, the inequality III < II < I lists the given values in increasing order.
AP Calculus BC Practice Test: Integration and Accumulation of Change
Question
| A. | |
| B. | |
| C. | |
| D. |
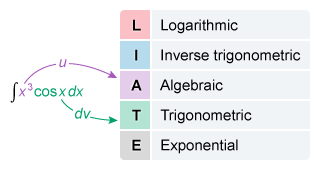
The functions cannot be rewritten algebraically or with u-substitution, so use integration by parts.
Explanation
The given integrand is the product of the functions x 3 and cos x. The functions cannot be rewritten algebraically or with u-substitution, so use integration by parts.
Follow the LIATE acronym to select u. Algebraic expressions (x3) are above trigonometric expressions (cos x),so let u = x3 and let dv = cos x dx (the remaining parts of the integrand).
Differentiate u = x3 and solve for du (see how), and integrate dv = cos x dx to find v. Substitute u = x3, v = sin x, and du = 3x2 dx into the formula for integration by parts and simplify.
| Integration by parts formula | |
| Plug in u = x3, v = sin x, and du = 3x2 dx | |
| Simplify and apply constant multiple rule |
Notice that the resulting expression matches one of the choices, so it is not necessary to integrate . From integration by parts, the given integral is equal to .
(Choice A) may result from mistakenly switching the expressions for u and du when substituting into the formula for integration by parts.
(Choice C) may result from mistakenly integrating each function in the given product individually.
(Choice D) may result from mistakenly applying the product rule for differentiation.
Things to remember:
If the integral of the product of two functions cannot be evaluated by u-substitution, use integration by parts:
Question
| A. | |
| B. e8 | |
| C. 3e8 | |
| D. divergent |
An improper integral of the form converges if exists.
Explanation
An integral in which one or both limits of integration is infinite is an improper integral.
To evaluate an improper integral of this form, replace the infinite limit of integration with the variable t and then calculate the limit as t approaches −∞ .
The integrand contains a composite function of the form eu, where u = x3. To use u-substitution, first differentiate u = x3 with respect to x and solve for dx to get (calculation).
The limits of integration must be changed to values of u, so plug the limits of integration into u = x3 to rewrite them as values of u. Substitute x3 = u, , and the new limits of integration into the given integral.
Now simplify the resulting integral to eliminate the remaining x-terms, integrate, and apply the Fundamental Theorem of Calculus (FTC).
| Resulting integral in terms of u | |
| Cancel and apply constant multiple rule | |
| Integrate natural exponential function | |
| Apply FTC |
Substitute the result above into the limit expression for the desired improper integral.
| Improper integral rewritten as a limit | |
| Substitute | |
| Apply constant multiple rule for limits | |
| Evaluate: | |
| Simplify |
Therefore, the value of the given integral is .
(Choice B) e8 may result from mistakenly substituting (instead of ) when rewriting the integral in terms of u.
(Choice C) 3e8 may result from mistakenly bringing out a constant multiple of 3 (instead of ) when applying u-substitution.
(Choice D) "Divergent" may result from assuming that an infinite limit of integration does not converge.
Things to remember:
To evaluate an improper integral, rewrite it as the limit of a definite integral:
Question
Which of the following expressions is equal to ) ) ?
| A. | |
| B. | |
| C. | |
| D. |
The value of a definite integral can be expressed in the form , which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width .
Explanation
The value of a definite integral can be expressed in the form , which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width :

The given limit appears to be in the form of the limit of a right Riemann sum where and . First, verify that the general function is and the subinterval width is (see how).
As n approaches infinity, the first term in a right Riemann sum approaches f(a), the value of f at the left endpoint of the interval [a, b]. The last term equals f(b), the value of f at the right endpoint of [a, b] (read more).
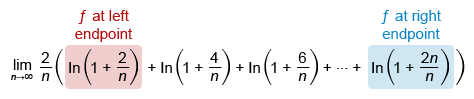
The left endpoint of the interval a is the lower limit of integration, and the right endpoint b is the upper limit of integration.
To determine which choice has the correct integrand f(x) and limits of integration [a, b], evaluate the limit as n approaches infinity of the first and last terms to find f(a) and f(b).

The choices include two possible integrands ln x and ln(1 + x). The values of f(a) and f(b) could correspond to either integrand, so find the values of a and b that yield ln 1 and ln 3, respectively, for each integrand.
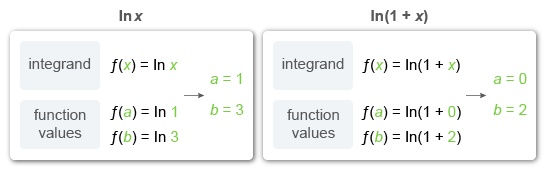
The given limit must equal or . Of these two integrals, only is an answer choice.
(Choice A) may result from incorrectly calculating limits of integration for the integrand ln x.
(Choice C) may result from incorrectly calculating the upper limit of integration for the integrand ln(1 + x).
(Choice D) may result from incorrectly calculating limits of integration for the integrand ln(1 + x).
Things to remember:
The value of a definite integral
can be expressed in the form
, which gives the limit at infinity of a right Riemann sum approximation with n subintervals of equal width
.
AP Calculus BC Practice Test: Differential Equations
Question
The number of catfish C raised on a catfish farm grow according to the logistic differential equation , where t is the time in years. If there are 250 catfish at time t = 0, for what value of C is the number of catfish growing most rapidly?
| A. 5000 | |
| B. 1000 | |
| C. 500 | |
| D. 0.4 |
A population P that is modeled by a logistic differential equation is growing most rapidly when P is equal to half the carrying capacity a.
Explanation
A logistic differential equation is of the form ), where P is a population, k is a constant, and a is the upper bound or carrying capacity.
A population P grows most rapidly when the graph of the logistic differential equation changes concavity from up to down at the point of inflection.
The most rapid growth of the population occurs when P is equal to half the carrying capacity a.
To determine the carrying capacity, first rewrite the given equation in the general form of a logistic differential equation.
The general form of a logistic equation has a 1 as the first term in the parentheses, so factor 0.4C out of the parentheses in the given equation.
| Given logistic differential equation | |
| Multiply and divide by 0.4C to factor | |
| Simplify: | |
| Rewrite 0.001 as a fraction to match general form |
Now compare the resulting differential equation to the general form to identify the value of the carrying capacity a.
Divide the carrying capacity a = 1000 by 2 to see that the number of catfish is growing most rapidly when C = 500.
(Choice A) 5000 may result from incorrectly dividing 0.0004 by 0.4 to get a carrying capacity of 10,000.
(Choice B) 1000 is the carrying capacity, but the question asks for the value of C for which the number of catfish is growing most rapidly.
(Choice D) 0.4 is the value of k in the factored form of the given differential equation, but the population grows most rapidly when C is equal to half the carrying capacity a.
Things to remember:
A quantity P with the logistic differential equation
) has its greatest rate of change when P is equal to half the carrying capacity a.
Question
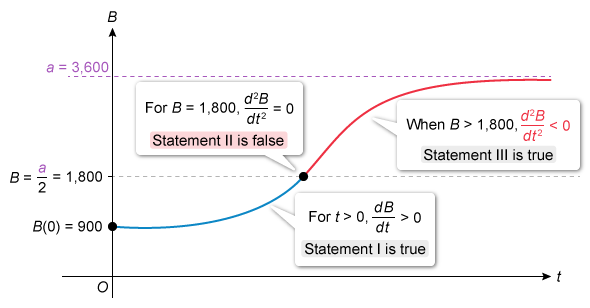
A population of butterflies B grows according to the logistic differential equation ), where t is the time in years and B(0) = 900. Which of the following statements are true?
I. For t > 0, .
II. For B = 900, .
III. When B > 1,800, .
| A. I only | |
| B. II only | |
| C. I and III only | |
| D. I, II, and III |
Consider the graph of the given logistic differential equation to analyze each statement.
Explanation
The solution to a logistic differential equation of the form ) with the initial condition P(0) = c has an upper bound or carrying capacity of a.
The graph of P(t) always increases, so . When , the graph changes concavity from up to down at a point of inflection, so .
To determine which of the statements are true, first compare the given equation to the general form of the logistic differential equation and identify the carrying capacity a.
The carrying capacity of the given equation is a = 3,600. Use the value of a to determine the point of inflection and sketch a graph of the logistic differential equation with the given initial condition of B(0) = 900.
Therefore, only statements I and III are true.
Things to remember:
The general form of the logistic differential equation for the quantity P with carrying capacity a is
).
Question
Let y = f(x) be the solution to the differential equation with initial condition f(2) = 1. What is the approximation for f(1) obtained by using Euler's method with two steps of equal length, starting with x = 2 ?
| A. −1 | |
| B. | |
| C. | |
| D. |
To approximate the y-value of a solution to a differential equation using Euler's method, first determine the step size.
Explanation
Euler's method is a numerical method used to approximate a solution of a differential equation of the form with an initial condition (x0, y0).
To approximate the y-value of a solution using Euler's method with n steps of equal length, apply the following recursive formula n times:
First subtract the given initial x-value (2) from the final x-value (1), and then divide the result by n = 2 to determine the step size .
Set up a table beginning with n = 0 and ending with n = 2, and enter the initial values x0 = 2 and y0 = 1. Add to the x-value from the previous step to get the x-value for the next step.
Now determine the new y-value yn + 1 in each step. Plug the current point (xn, yn) into f ′(xn, yn) = x + 2y, and then plug and the values of f ′(xn, yn) and yn into the Euler's method equation.
The approximation for f(1) obtained by using Euler's method with two steps of equal length, starting with x = 2, is .
(Choice A) is the approximation of ) obtained by using Euler's method with one step, but the question asks for the Euler's method approximation for f(1) with two steps.
(Choice C) is the approximation of ) obtained by using Euler's method with three steps, but the question asks for the Euler's method approximation for f(1) with two steps.
(Choice D) may result from mistakenly calculating Euler's method with a step size of instead of .
Things to remember:
To approximate the y-value of a solution to a differential equation using Euler's method with n steps of equal length, apply the following recursive formula n times:
AP Calculus BC Practice Test: Applications of Integration
Question
Which of the following is the volume of the solid generated by revolving the region bounded by the lines y = 2x + 1, y = x + 1, and x = 3 about the x-axis?
| A. | |
| B. | |
| C. | |
| D. |
Explanation
To determine whether to use the disc or washer method, graph the given lines to see if there is space between the region and the x-axis.
There is space between the region and the axis of revolution, so it is necessary to use the washer method to find the volume.
The top function is y = 2x + 1 and the bottom function is y = x + 1, so R(x) = 2x + 1 and r(x) = x + 1. The region spans the interval of x-values [0, 3], so the limits of integration are 0 and 3. Substitute the function and limits into the integral for the washer method and evaluate.
| Washer method integral | |
| Substitute functions and limits | |
| Expand binomials | |
| Combine like terms | |
| Integrate | |
| Apply FTC | |
| Simplify |
Therefore, the volume of the solid is
Question
Which of the following gives the area of the region R bounded by the graph of y = ln x + 1 and the lines y = 3, x = 1, and x = e ?
| A. | |
| B. | |
| C. | |
| D. |
Explanation
It is given that the region R is bounded by the vertical lines x = 1 and x = e, so the area integral spans the interval [1, e]. Eliminate Choices A and B.
Region R is the area between the functions y = ln x + 1 and y = 3 on the interval [1, e]. To determine which is the top function and which is the bottom function, plug the endpoints of the interval into y = ln x + 1 and compare the resulting values to y = 3.
| y = ln x + 1 | Given function | y = ln x + 1 |
| y = ln 1 + 1 | Plug in given x-values | y = ln e + 1 |
| y = 0 + 1 | Evaluate logarithms | y = 1 + 1 |
| y = 1 | Add | y = 2 |
The function y = ln x + 1 is an increasing function that is less than 3 for x = 1 and x = e. Therefore, y = 3 must be the top function and y = ln x + 1 must be the bottom function.
Substitute the functions f(x) = 3 and g(x) = ln x + 1 and the endpoints a = 1 and b = e into the formula for the area between two curves to find the integral that gives the area of region R.
| Area of region R | |
| Substitute functions and values | |
| Distribute −1 and combine constants |
The integral that gives the area of region R is (graph).
Question
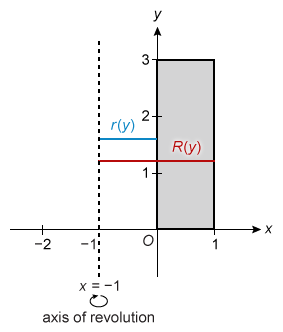
A program defines the dimensions of a certain coupling for a three-dimensional printer. The coupling is defined as the rectangular area bound between x = 1, y = 3, and the x- and y-axes revolved around the vertical line x = −1. What is the volume of the coupling?
| A. 3𝜋 | |
| B. 9π | |
| C. 12π | |
| D. 15π |
Explanation
It is given that the area revolves around a vertical line, so the volume integral is in terms of y.
Graph the given area and the axis of revolution to determine whether to use the disc or washer method.
There is space between the given area and the axis of revolution, so it is necessary to use the washer method.
The radii of each washer are R(y) = 1 − (−1) = 2 and r(y) = 0 − (−1) = 1, and the area spans the interval of y-values [0, 3]. Plug these values into the washer method volume integral and evaluate.
| Washer method integral | |
| Plug in R(y) = 2, r(y) = 1, y1 = 0, and y2 = 3 | |
| Simplify integrand | |
| Integrate | |
| Apply FTC | |
| Simplify |
Therefore, the volume of the coupling is
AP Calculus BC Practice Test: Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Question
If h is a vector-valued function defined by , then hʹʹ(t) =
| A. | |
| B. | |
| C. | |
| D. |
The second derivative of the vector-valued function h is the vector containing the second derivatives of each component of h.
Explanation
The second derivative of the vector-valued function h is the vector containing the second derivatives of each component of h.
To find the components of hʹʹ, differentiate each component of the given vector-valued function twice.
Use the chain rule to differentiate the composite function x(t) = e4t, and use the power rule to differentiate y(t) = t4 to find the components of hʹ.
The components of hʹ are xʹ(t) = 4e4t and yʹ(t) = 4t3. Now use the chain rule to differentiate xʹ(t), and use the power rule to differentiate yʹ(t) to find the components of hʹʹ.
Therefore, the second derivative of the given vector-valued function is .
(Choice A) may result from incorrectly applying the power rule to differentiate yʹ(t) = 4t3.
(Choice C) is the first derivative of h, but the question asks for the second derivative.
(Choice D) may result from not applying the chain rule when differentiating xʹ(t) = 4e4t.
Things to remember:
The derivative of a vector-valued function
is the vector of the derivatives of each component of f.
Question
If and , for t > 0, what is in terms of t ?
| A. | |
| B. | |
| C. | |
| D. |
To find the second derivative of a parametrically defined function in terms of t, first find in terms of t.
Explanation
The notation represents the second derivative of y with respect to x. To find the second derivative of a parametrically defined function in terms of t, first divide by to find in terms of t.
Then differentiate with respect to t and divide the result by :
Differentiate the equations for x and y independently with respect to t to find and . First use a negative exponent to rewrite the y equation as t−1.
| Given equations for x(t) and y(t) | ||
| Apply power rule to differentiate |
Now divide the expression for by the expression for to find .
| Parametric first derivative | |
| Substitute and | |
| Multiply by the reciprocal and simplify |
Differentiate with respect to t and then divide the result by . Use a negative exponent to rewrite the first derivative as and then differentiate with respect to t.
| First derivative | |
| Differentiate and simplify |
Now plug in and into the equation for and simplify.
| Parametric second derivative | |
| Substitute and | |
| Multiply by the reciprocal and simplify |
Therefore, .
(Choice B) may result from not dividing by .
(Choice C) is the first derivative of the parametric function , but the question asks for the second derivative .
(Choice D) is the result of mistakenly dividing by to determine .
Things to remember:
To find
in terms of t for a parametrically defined function, differentiate
with respect to t and then divide the result by
:
Question
A particle moves along the -plane with position given by the parametric equations x(t) = t2 – 7 and y(t) = 8 – 2t. In which direction is the particle moving as it passes through the point (−3, 4) ?
| A. Up and to the left | |
| B. Down and to the left | |
| C. Up and to the right | |
| D. Down and to the right |
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).
Explanation
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).
Differentiate the given equations x(t) and y(t) with respect to to write equations for x'(t) and y'(t).
| Given equations for x and y | ||
| Differentiate |
Since y'(t) < 0 for all t, the particle is moving down for all t. It is possible to eliminate choices A and C.
To determine the horizontal direction of the particle as it passes through the point (−3, 4), it is first necessary to find the value of for which the position of the particle is (−3, 4). Substitute x(t) = −3 and y(t) = 4 and then solve each equation to find the value of that satisfies both equations.
Therefore, the particle passes through the point (−3, 4) when t = 2.
It was shown above that the particle is moving down for all t. Plug t = 2 into x'(t) to determine if the particle is moving to the left or to the right when it passes through the point (−3, 4).
| Equation for | |
| Plug in |
Since x'(2) > 0, the particle is moving to the right at time t = 2.
Therefore, when the particle passes through the point (−3, 4) it is moving down and to the right.
(Choice A) "Up and to the left" may be the result of mistakenly using the signs of y'(t) to determine the horizontal direction and x'(t) to determine the vertical direction.
(Choice B) "Down and to the left" may be the result of mistakenly plugging in the coordinates of the given point x = −3, y = 4 for the value of t in the equations for x'(t) and y'(t).
(Choice C) "Up and to the right" may be the result of an error when differentiating x'(t) .
Things to remember:
To determine the direction of a moving particle whose position is given by parametric equations x(t) and y(t), analyze the signs of the velocity equations x'(t) and y'(t).
AP Calculus BC Practice Test: Infinite Sequences and Series
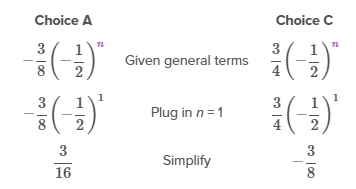
Question
If the first term of a geometric series is , which of the following series converges to ?
| A. | |
| B. | |
| C. | |
| D. |
The value to which a geometric series converges is equal to the sum of the geometric series.
Explanation
A geometric series is of the form , where a is a constant and r is the common ratio.
The value to which a geometric series converges is equal to the sum of the geometric series, where S is the sum, a1 is the first term, and r is the common ratio.
To determine which series has a first term a1 of and a sum of (converges to) , first calculate the common ratio. Plug the values of a1 and S into the formula above and solve for r.
The common ratio is , so the series will be of the form . Eliminate Choices B and D because they do not have a common ratio of .
Now plug n = 1 into arn for the remaining two series to see which has a first term of .
Therefore, the series that converges to with a first term of is .
(Choice A) may result from assuming that a in the general series is equal to the first term a1, but a from the general formula is a different constant because the series starts at n = 1.
(Choice B) converges to , but the first term is instead of .
(Choice D) has a first term of , but converges to instead of .
Things to remember:
- A geometric series is of the form , where r is the common ratio.
- The value to which a geometric series converges is equal to the sum of the geometric series, where S is the sum, a1 is the first term, and r is the common ratio.
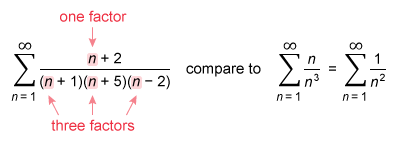
Question
Which of the following series converge?
| I. | II. | III. |
| A. I only | |
| B. II only | |
| C. II and III only | |
| D. I, II, and III |
If the general term an of a series includes an n in a factorial or an exponent, the ratio test may be used to determine its convergence.
Explanation
To determine the convergence of the given series, first determine which convergence test should be used.
Series I and II
The first two given series contain n in a factorial, so use the ratio test to determine their convergence. Evaluate for each series and determine whether the result is less than 1.
Find an+1 for each series (calculations). Then substitute the expressions for an and an+1 into the ratio test limit for both series, and compare the degrees to evaluate the resulting limits.
Series I diverges because and Series II converges because 0 < 1. It is possible to eliminate Choices A and D because they include Series I.
Series III
The third series is a rational expression with a higher degree in the denominator, so use the limit comparison test and compare the series with an appropriate p-series to determine its convergence.
To choose a p-series for comparison, disregard all but the number of factors of n in both the numerator and denominator of the given rational series. Simplify the result, if possible.
The comparison series is a p-series with p = 2, so it converges. Apply the limit comparison test , where and . Then compare the growth rates of the individual terms.
The limit is positive and finite and converges, so Series III converges. It is possible to eliminate Choices A and B because they do not include Series III.
Therefore, only Series II and III converge.
Things to remember:
-
If the general term an of a series includes an n in a factorial or an exponent, use the ratio test to determine its convergence.
-
Use the limit comparison test to determine the convergence or divergence of an infinite series that closely resembles a p-series by comparing the series to a simpler function.
Question
Which of the following series are absolutely convergent?
| A. II only | |
| B. III only | |
| C. I and II only | |
| D. I and III only |
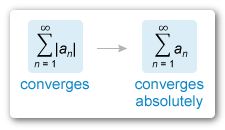
A series is absolutely convergent if converges.
Explanation
A series is absolutely convergent if converges.
To determine which of the given series converges absolutely, first find the absolute value of an for each series. For positive integer values of n, |(−1)n| = 1 and the value of each resulting fraction is positive.
Now choose an appropriate convergence test to determine whether each series converges or diverges.
Series I
The resulting series is the harmonic series, which diverges. The series diverges, so Series I does not converge absolutely. Therefore, it is possible to eliminate Choices C and D because they include Series I.
Series II
Apply the nth term test and compare the rates of growth to determine the convergence of the resulting series.
The limit is infinite, so the series diverges and Series II does not converge absolutely. Therefore, it is possible to eliminate Choices A and C because they include Series II.
Series III
Use exponent rules to rewrite the resulting series in the general form of a geometric series (calculation) and identify the value of the common ratio r.
The series is geometric, with a common ratio of . Therefore, the series converges since |r| < 1. Series III converges absolutely, so it is possible to eliminate Choices A and C because they do not include Series III.
Therefore, the series that is absolutely convergent is III only.
Things to remember:
A series
is absolutely convergent if
converges.
Make the AP Calculus BC Exam Feel Like Practice
Our AP Calculus BC practice tests and quizzes with MCQs and FRQs* that are just like the exam. They’ll help you think critically and spot trick answers, handle pressure and boost your confidence for test day!
One-Click AP
Calc BC Quizzes
Simulate Real Exam Conditions
Study with Exam-Aligned Questions
Ready to Get Started?
AP Calc BC practice tests with MCQ and FRQ questions designed to match the real exam.
Score Higher with Quality Learning Tools
Detailed Explanations for Every AP Calculus BC Question
Understand the “why” behind every answer with clear, step-by-step solutions that walk you through the logic and math behind each problem. Every AP Calculus BC practice question and FRQ includes detailed explanations, formulas, and worked-out examples so you can see exactly how to solve even the toughest calculus problems. You’ll also get tips for avoiding common mistakes and recognizing tricky question types that often appear on the exam. Instead of just memorizing procedures, you’ll build a deep understanding of calculus concepts—helping you approach any problem with confidence on test day.
Flashcards & Notes That Help You Actually Remember
Create digital flashcards to practice the concepts you struggle with most, like applying the ratio test or finding a Taylor series, so you remember them for the AP Exam, not just the next quiz. Use My Notebook to organize key ideas from AP Calculus BC practice questions in the format that works best for you—whether that’s bullet points for integration techniques, diagrams of slope fields, or detailed notes on parametric and polar functions. One-click transfer from explanations to your flashcards or notebook keeps everything you need in one organized place.
Track Your Progress & Crush Your Weak Spots
Stay on top of your AP Calculus BC prep with smart performance tracking across all your AP Calculus BC practice tests and practice questions. Our powerful analytics dashboard breaks down your results by topic so you can see what you’ve mastered and what still needs work. Focus your energy where it counts, skip the material you already know, and watch your AP Calculus BC scores soar.
Choose How You Study and Save
Choose How You Study and Save
Whether you need a focused study guide or a comprehensive prep course, we have you covered!
Everything you need to pass the AP Calc BC exam
AP Calculus BC
Practice Tests
Starting at $39
1800+ AP Calculus BC Practice Questions (MCQs)
Custom AP Calc BC Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
Realistic FRQ Practice with Scoring Guide*
1800+ AP Calculus BC Practice Questions (MCQs)
Custom AP Calc BC Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
Realistic FRQ Practice with Scoring Guide*
Score-Predicting Full-Length AP Calc BC Mock Exam*
Print and Digital Study Guide
200+ Check-for-Understanding Questions
Expert-Led Video Lessons
* Coming Winter 2025/Spring 2026
AP Calc BC Practice Test Reviews
Here’s what our students have to say after using our practice tests to study for their AP Biology exam.
UWorlds multiple choice questions are similar to the ones on the official AP exam and allowed me to time myself for each question. This was very helpful for me as I was able to answer questions faster and could finish the questions on the actual exam. The explanations for each question went in-depth and gave important details pertaining to events in the timeline. Through this, I was able to gain important skills for the exam and get a 5.
Before, I had a hard time studying and staying focused because it was just boring, but now with UWorld, not only can I focus, but I actually feel motivated to learn!
The explanations were clear and I could practice the question based on units. I got a 5 in the end!! So, I think it’s very helpful and I’ll be using it to study for my future exams 🙂 You guys provide so many different functions to help students like me, and I really appreciate it, it’s really worth the money.
AP English Language Practice Tests from UWorld:
Frequently Asked Questions (FAQs)
Do UWorld’s AP Calculus BC practice tests include every unit and topic covered on the exam?
Yes, they do. Our AP Calculus BC practice tests are built to fully match the latest College Board® Course and Exam Description (CED). Every unit and topic is represented, ensuring complete coverage of what you will encounter on test day.
The UWorld question bank includes all key areas of AP Calculus BC, such as:
- Limits, Continuity, and Differentiation
- Applications of Derivatives
- Integration and the Fundamental Theorem of Calculus
- Differential Equations and Slope Fields
- Parametric, Polar, and Vector Functions
- Infinite Sequences and Series
- Polynomial Approximations and Taylor Series
You can use our customizable quiz builder to create AP Calc BC practice tests focused on a single concept or mix topics for a cumulative review.
How often does UWorld update its AP Calculus BC practice test questions?
Our AP Calculus BC practice test questions are reviewed and updated continuously to remain aligned with the most recent College Board® standards. A team of experienced math educators and AP experts regularly evaluates question content, wording, and explanations to reflect the latest trends in exam design.
We carefully track official updates from the College Board®, including any curriculum or format changes, so you always have access to realistic and up-to-date practice materials. UWorld’s AP Calc BC practice questions ensure that your study time is focused on accurate, exam-level problems rather than outdated content.
How can UWorld’s AP Calculus BC practice tests help me earn a high score?
UWorld’s AP Calculus BC practice tests are designed to help you develop mastery through active learning. Each question challenges you to think critically, apply calculus principles, and strengthen your problem-solving skills.
Here’s how our approach helps you excel:
- Build Real Exam Skills: Practice with hundreds of questions modeled on actual AP test difficulty and style.
- Learn Through Explanation: Every question includes detailed, step-by-step solutions that explain the reasoning behind each answer choice.
- Track and Improve: Performance analytics show your strongest and weakest topics so you can target specific areas for improvement.
Each AP Calc BC practice test turns review time into meaningful learning that builds confidence for test day.
Are UWorld’s AP Calculus BC practice tests realistic compared to the real exam?
Yes. UWorld’s AP Calculus BC practice tests are carefully written by experienced educators to mirror the College Board® exam as closely as possible.
Our platform simulates the exam experience with:
- Multiple-Choice Questions (MCQs): Modeled after real AP questions that assess both procedural accuracy and conceptual understanding.
- Free-Response Questions (FRQs)*: Multi-part problems that include complete scoring rubrics and explanations.
- Timed Practice Sessions: Optional timing modes that help you manage pacing and build endurance for the 3-hour and 15-minute exam.
With UWorld’s AP Calc BC practice tests, you’ll gain experience and confidence under conditions that closely match the real test.
Can I build my own AP Calculus BC practice tests by topic?
Absolutely. UWorld’s platform lets you create fully customized AP Calculus BC practice tests that match your personal study plan. You can select questions by topic, difficulty, or question type to focus on exactly what you need to strengthen.
Here are a few ways students use this feature:
- Review a single unit: If you just covered “Series and Convergence,” build an AP Calc BC mock exam focused only on that topic. You can zero in on AP Calc BC Series FRQs for targeted practice.
- Mix specific topics: Combine questions from “Derivatives,” “Integrals,” and “Parametric Functions,” including AP Calc BC parametric FRQs, to prepare for a midterm.
- Simulate a full exam: Use questions from all AP Calc BC units in timed mode for a realistic test-day experience.
This level of control makes it easy to target weak areas and reinforce your understanding of every concept in AP Calculus BC.
What makes UWorld’s AP Calculus BC QBank different from free question sets online?
While free question sets may look appealing, the UWorld AP Calculus BC QBank offers a much deeper and more effective learning experience.
Here’s why students prefer UWorld:
- Expert-Crafted Explanations: Free resources often only show the right answer. UWorld provides detailed, step-by-step rationales for each answer choice so you can learn the reasoning behind every solution.
- Guaranteed Accuracy: All AP Calc BC practice questions are written and updated by professionals who align every problem with the latest College Board® Course and Exam Description.
- Interactive Learning Tools: Instead of static question lists, UWorld gives you performance analytics, progress tracking, and customizable quizzes that adapt to your needs.
Free materials might help with exposure, but UWorld’s AP Calculus BC QBank delivers the quality and precision that lead to true mastery.
When should I begin using AP Calculus BC practice questions in my prep?
You can start using UWorld’s AP Calculus BC practice questions at any stage of your preparation.
- Before the school year: Begin early to preview core topics and strengthen your foundation.
- During the year: Create quizzes that align with your class lessons, such as a short set on “Integration Techniques” or “Series.”
- Before the exam: Take full-length AP Calc BC practice tests to identify weak spots and refine your pacing.
Whether you have several months or just a few weeks, UWorld’s adaptive practice system helps you get the most out of every study session.
What score on AP Calculus BC practice tests shows you are ready for the real exam?
There is no single perfect score, but consistent performance and strong conceptual understanding are key. For most students, regularly scoring around 70% to 75% on UWorld’s AP Calculus BC practice tests is a good sign of readiness.
Beyond the numbers, you’ll know you are prepared when you can:
- Identify the calculus concept behind each question quickly.
- Explain both the correct and incorrect answer choices with confidence.
- See balanced performance across all AP Calc BC units on your progress dashboard.
UWorld’s platform helps you track growth and mastery so that your AP Calculus BC practice questions translate into top results on test day.
Where can I access free AP Calculus BC practice questions?
You can try free AP Calculus BC practice questions by signing up for UWorld’s 7-day free trial. This gives you access to a sample of our expert-written multiple-choice and free-response questions, each with detailed explanations that show how to approach and solve them effectively.
The free trial also offers a glimpse of our complete AP Calc BC learning experience, which includes in-depth video lessons and digital study resources designed to help you strengthen your calculus skills and prepare confidently for the exam.
Do UWorld’s AP Calculus BC practice tests include both Multiple-Choice and Free-Response Questions?
Yes. UWorld’s AP Calculus BC practice tests include a wide range of both multiple-choice and free-response questions that reflect the exact structure and rigor of the official exam.
The free-response questions (FRQs)* come with clear scoring guidelines and step-by-step sample solutions, so you can learn how to organize your work and show reasoning in the same way AP graders expect. Practicing both formats helps you master pacing, accuracy, and presentation for every section of the test.