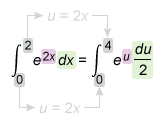Bundle 3+ College Prep products for 20% off

AP® Calculus AB Unit 8 Review and Practice Test

Applications of Integration

Get exam-ready with our AP® Calculus AB Unit 8 review. Explore integration applications, solve real-world problems, and practice with the Unit 8 AP Calc AB progress checks and FRQs.

AP Calculus AB prep course suite by UWorld

Your Go-To Guide for AP Calculus AB Unit 8

Simplify integration with clear lessons, visual examples, and Unit 8 AP Calc AB progress checks. Strengthen your understanding before tackling full-length exams.

Watch

Engaging Video Lessons

Learn faster with bite-sized videos that break down tough Unit 8 Calculus AB topics like area and volume using clear visuals and examples. Each lesson connects directly to the AP Calc AB Unit 8 Progress Check MCQ Part A, helping you understand how concepts appear on the exam. With guided walkthroughs and real test-style problems, you’ll grasp integration applications more easily.

Preview Video Lesson
Buy Now
UWorld’s AP Calc AB Video Lessons and Online Study Guide
UWorld’s AP Calculus AB Study Guide Prep book
Read

Interactive Study Guides

Stay organized with interactive AP Calculus AB Unit 8 review materials that simplify key formulas and problem types. These Unit 8 AP Calc AB review guides combine notes, visuals, and checkpoints so you can study smarter, not longer. Use them alongside your Calc AB Unit 8 lessons to track progress and build confidence before test day.

Preview Book
Buy Now
Practice

Practice What You’ve Learned in AP Calc AB Unit 8

Put your knowledge to the test with AP Calc AB Unit 8 practice questions that mirror real exam formats. Solve MCQs and FRQs on integration, area, and volume to see how well you understand each concept. Each Unit 8 AP Calc AB FRQ is designed to strengthen problem-solving speed and accuracy before exam day.
Try these sample practice questions with detailed answer explanations:
Applications of Integration Practice Tests

Question

Rain is falling at the rate of r (t) = 3 e - 0.2 t inches per hour, where t is the time in hours since the rain began to fall. Which of the following gives the amount of rain, in inches, that falls from time t = 0 to time t = 6 hours?

A. 3 e - 1.2 - 3
B. 0.6 - 0.6 e - 1.2
C. 3 - 3 e - 1.2
D. 15 - 15 e - 1.2

Hint :

The definite integral of a rate of change of a quantity over an interval gives the amount of change in the quantity over the interval.

Explanation

The definite integral of a rate of change r(t) of a quantity over an interval of time from t1 to t2 gives the amount of change in the quantity over the interval.

∫ t 1 t 2 r (t)   d t = amount of change (net change) in quantity from t1 to t2

Since r (t) = 3 e - 0.2 t is the rate of change of the rainfall, the amount of rain that falls between times t1=0 and t2=6 is given by

∫ 0 6 3 e - 0.2 t d t

The integrand above is a composite function of the form e u where u = −0.2t is the inside function, so use u -substitution to integrate.

First differentiate u = −0.2t with respect to t to find dt in terms of u .

u = - 0.2 t Equation for u
d u d t = - 0.2 Differentiate both sides with respect to t
d u = - 0.2 d t Multiply both sides by dt
d u - 0.2 = d t Divide both sides by −0.2

Calculate the limits of integration in terms of u and then substitute u = - 0.2 t , d u - 0.2 = d t , and the new limits of integration into the integral.

Definite integral expression derived from a rate of change problem, ready for evaluation using the Fundamental Theorem of Calculus

Now use the Fundamental Theorem of Calculus (FTC) to evaluate the resulting integral.

∫ 0 - 1.2 3 e u d u - 0.2 Integral for amount of rain in terms of u
3 - 0.2 ∫ 0 - 1.2 e u d u Constant multiple rule: ∫ k f ( x ) d x = k ∫ f ( x ) d x
- 15 ∫ 0 - 1.2 e u d u Simplify: 3 - 0.2 = 3 ÷ - 2 10 = 3 ⋅ - 10 2 = 3 ⋅ - 5 = - 15
- 15 e u | 0 - 1.2 Integrate: ∫ a b e u d u = e u | a b
- 15 e - 1.2 - ( - 15 e 0 ) Apply the FTC
15 - 15 e - 1.2 Simplify: e 0 = 1 → - ( - 15 e 0 ) = 15 .   Rearrange terms to match answer choice

Therefore, the amount of rain in inches that falls from time t=0 to time t=6 hours is given by 15 - 15 e - 1.2

(Choice A) 3 e - 1.2 - 3 may be a result of neglecting to integrate the function or incorrectly integrating before applying the Fundamental Theorem of Calculus. This value is negative, which is not a valid option for the context of the question.

(Choice A) 0.6 - 0.6 e - 1.2 may be a result of differentiating rather than integrating the function before applying the Fundamental Theorem of Calculus.

(Choice C) 3 - 3 e - 1.2 may be a result of neglecting to integrate the function or incorrectly integrating before applying the Fundamental Theorem of Calculus and then incorrectly applying the Fundamental Theorem of Calculus: ∫ a b f ′ (x) d x ≠ f (a) - f (b)

Things to remember:
The definite integral of a rate of change of a quantity over an interval gives the amount of change in the quantity over the interval.

Question

The base of a solid is the region in the first quadrant bounded by the graph of y = ex, the vertical line x = 2, and the x- and y-axes. For this solid, each cross section perpendicular to the x-axis is a square. What is the volume of the solid?

A. e 2 - 1
B. 1 2 e 4 - 1 2
C. e 4 - 1
D. 2 e 4 - 2

Hint :

The volume of a solid with cross sections of area A(x) perpendicular to the x-axis is given by ∫ x 1 x 2 A (x) dx

Explanation

The volume of a solid with cross sections of area A(x) perpendicular to the x-axis is given by a definite integral of A(x) in terms of x.

Diagram of a solid with square cross sections perpendicular to the x-axis, showing base region in the xy-plane bounded by y = e^x, x = 2, and the axes

Sketch the given boundaries of the region defined by the function y = ex, the line x = 2, and the x- and y-axes that form the base of the solid and determine the limits of integration.

The enclosed region spans the interval 0 ≤ x ≤ 2, so the limits of integration are x1 = 0 and x2 = 2.

Shaded region in the first quadrant bounded by y = e^x from x = 0 to x = 2, the x-axis, and the line x = 2

The cross sections are squares, so A(x) = s2 is the integrand.

The side length s of each cross section is the vertical distance between the top and bottom functions, so s = top − bottom. Substitute y = ex for the top and y = 0 for the bottom and simplify.

Step-by-step derivation showing side length s = e^x − 0 = e^x, then area A(x) = (e^x)^2 = e^{2x}

To find an expression for the area function A ( x ) , plug s = e x into the formula for the area of a square to get A ( x ) = ( e x ) ² = e 2 x . Substitute A ( x ) = e 2 x , x 1 = 0 , and x 2 = 2 into the volume integral to get ∫ 0 2 e 2 x d x .

The integrand e 2 x is a composite function of the form e u , where u = 2 x , so rewrite the integral in terms of u. The derivative of u is d u d x = 2 , so solve for dx = du 2 . Plug the limits of integration for x in u = 2 x to get 0 and 4.

Final definite integral setup: V = ∫ from 0 to 2 of e^{2x} dx, ready for evaluation

Apply the constant multiple rule to rewrite the resulting integral as  1 2 ∫ 0 4 e u du , then integrate and apply the Fundamental Theorem of Calculus (FTC).

V = 1 2 ∫ 0 4 e u du Resulting integral
V = 1 2 [ e u ] 0 4 Integrate
V = 1 2 [ e 4 - e 0 ] Apply FTC
V = 1 2 e 4 - 1 2 Simplify e0 = 1 and distribute 1 2

Therefore, the volume of the solid is 1 2 e 4 − 1 2 .

(Choice A) e 2 − 1 may result from not squaring the side length in the formula for the area of a square.

(Choice C) e 4 − 1 may result from not integrating with u-substitution.

(Choice D) 2 e 4 − 2 may result from finding an incorrect expression of d x ≠ 2 d u (instead of dx = du 2 ) when applying u-substitution.

Things to remember:
The volume of a solid with cross sections of area A ( x ) perpendicular to the x-axis is given by ∫ x₁ x₂ A ( x ) d x .

Question

What is the area of the region R bounded by the graphs of x = y2 − y + 1 and x = y + 1 ?

A. 4 3
B. 8 3
C. 4
D. 20 3

Explanation

The area between the given functions is equal to the integral of the right function minus the left function between the y-values of their intersection points, so it is necessary to determine which are the right and left functions and to find the intersection points.

The quadratic function has a positive leading coefficient, so the parabola opens to the right. All the choices are finite values, so the linear function must cross to the right of the quadratic (graph). Set the expressions equal and solve for y to find where they intersect.

y2 − y + 1 = y + 1 Set functions equal
y2 − 2y = 0 Subtract y and 1 from both sides
y(y − 2) = 0 Factor out GCF
y = 0 and y = 2 Apply zero product property

Therefore, the right function is f(y) = y + 1 and the left function is g(y) = y2 − y + 1, and they intersect at y = 0 and y = 2.

Integrate the difference between the functions on the interval of their intersection points to find the area of region R.

∫ a b ( f ( y ) - g ( y ) ) dy Area of region R
∫ 0 2 ( y + 1 - ( y 2 - y + 1 ) ) dy Substitute functions and values
∫ 0 2 ( 2 y - y 2 ) dy Combine like terms
[ y 2 - 1 3 y 3 ] 0 2 Integrate
2 2 - 1 3 ( 2 ) 3 - ( 0 2 - 1 3 ( 0 ) 3 ) Apply FTC
4 - 8 3 - 0 Simplify terms
4 3 Subtract

Therefore, the area of region R is  4 3 .

Buy Now
UWorld Dark Blue logo

Learn on the Go with Smart Practice Tools

Stay on track wherever you are with quick quizzes and mini-reviews from the AP Calculus AB Unit 8 Progress Check MCQ Part B. Test your understanding of integration, and tackle AP Calc AB area and volume FRQs for extra challenge. With flexible access and instant feedback, reviewing Unit 8 AP Calc AB concepts has never been easier.

App Store
Google Play

Stand Out
with a Top Score in AP Calculus AB

Finish your AP Calculus AB Unit 8 review and continue mastering all units with UWorld. Boost your performance and make yourself a standout candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc AB Videos
  • Print & Digital Study Guide
  • 1400+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards
  • Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calculus AB Unit 8 focuses on applying integration concepts to real-world and geometric problems. You’ll explore how integrals can represent accumulated quantities, areas, and volumes, ideas that connect directly to motion, growth, and physical models.

Key topics include:

  • Determining the average value of a function using definite integrals: Learn to calculate the mean height or output of a function over an interval.
  • Modeling particle motion: Understand how velocity, acceleration, and position are linked through integration.
  • Solving accumulation problems: Use integrals to determine how quantities build up over time.
  • Finding the area between curves: Integrate the difference between two functions to find the space enclosed between them.
  • Determining volume with cross-sections, the disc method, and the washer method: Apply integration to compute 3D volumes generated by rotating or stacking shapes.

Mastering these topics requires both conceptual understanding and consistent practice. UWorld’s AP Calculus AB Unit 8 review provides clear explanations, visual breakdowns, and step-by-step problem solutions to strengthen your foundation. With realistic AP-style questions and instant feedback, you’ll learn how to apply integration techniques with confidence on the actual exam.

The most effective approach to prepare for AP Calculus AB Unit 8 is the Read, Watch, Practice method:

  • Read: Go through your notes and focus on integration techniques, including volume by revolution and accumulation. Summarize key formulas in your own words.
  • Watch: Use short video lessons to visualize how integration applies to motion, area, and solids. Seeing examples makes abstract ideas easier to grasp.
  • Practice: Apply what you learn with UWorld’s AP Calc AB Unit 8 practice tests, which include MCQs and FRQs modeled after the actual exam.

After each session, review the detailed explanations to identify where you went wrong and why. UWorld’s adaptive approach helps you focus on weak areas, improving accuracy and speed. Pairing your study schedule with UWorld’s AP Calculus AB review course gives you access to structured lessons and real exam-level questions that make test prep efficient and effective.

Yes! You can start preparing for AP Calculus AB Unit 8 with a mix of free and trial-based resources:

  • UWorld: Gives you access to a free 7-day trial, letting you experience premium-quality questions, detailed rationales, and visual explanations.
  • College Board’s AP Classroom: Offers sample Unit 8 progress check MCQs and topic outlines.
  • Khan Academy: Provides free video lessons and problem walkthroughs on integration.

While free tools like Khan Academy help you review concepts, UWorld’s trial gives you access to realistic practice that mirrors the AP Calc AB Unit 8 test format. The explanations don’t just show the right answer, they teach the why behind it. Start your UWorld free trial to see how structured study and interactive feedback can help you prepare with confidence.

The AP Calc AB Unit 8 test assesses your ability to apply integration concepts to real-world scenarios. Expect two main formats:

  • Multiple-Choice Questions (MCQs): Covering topics like the area between curves, accumulation, and solids of revolution.
  • Free-Response Questions (FRQs): Requiring detailed written solutions and explanations of your process.

You may also encounter AP Calc AB Unit 8 Progress Check MCQ Part A or Part B, testing conceptual understanding and application speed. To prepare, use UWorld’s AP Calculus AB Unit 8 practice questions. Each problem is crafted to mimic exam difficulty and includes thorough explanations that break down every step. By solving both MCQs and FRQs in UWorld’s format, you’ll strengthen your reasoning and build confidence under timed conditions.

Improving your FRQ score in AP Calculus AB Unit 8 means mastering how to explain your reasoning clearly and efficiently. Here’s how to approach it:

  • Understand the problem type: FRQs often include area and volume integrations or motion-based applications.
  • Show every step: Partial credit is awarded for correct reasoning, even if your final answer is off.
  • Use clear notation: Write integrals and limits precisely.
  • Review feedback: Analyze your past mistakes to learn where your reasoning fell short.

UWorld’s AP Calc AB Unit 8 FRQs are modeled after real exam prompts and come with detailed walkthroughs showing how to structure complete, high-scoring responses. Practicing regularly helps you build both speed and precision, turning complex problems into familiar patterns. The more you work through UWorld’s question bank, the more confident you’ll feel tackling any FRQ on test day.

The Applications of Integration unit, or AP Calculus AB Unit 8, makes up roughly 10–15% of the total AP exam score. This portion evaluates your ability to apply integration to geometry, physics, and motion problems—key areas that bridge earlier units with real-world applications.

Since this unit holds a significant percentage, mastering it can greatly impact your overall score. You’ll encounter related questions not just in MCQ Part A and Part B, but also across multiple FRQs in the free-response section.

To strengthen your performance, use UWorld’s AP Calculus AB Unit 8 progress checks and full-length tests. The platform mirrors actual exam conditions, helping you track progress, identify weak spots, and reinforce essential formulas. With consistent UWorld practice, you can turn this high-weight unit into a scoring advantage.

A good AP Calc AB Unit 8 study guide should simplify complex integration concepts and offer structured practice. It should include:

  • Topic summaries and formula sheets for quick recall
  • Step-by-step examples for area and volume applications
  • Practice questions modeled on AP-style MCQs and FRQs

UWorld’s AP Calculus AB Unit 8 study materials check all these boxes, combining concise explanations with problem-solving practice that reflects the real exam. You can preview these tools with the UWorld 7-day free trial, perfect for getting a feel for the platform’s detailed solutions and visual learning tools before you commit.

With its mix of theory and application, UWorld’s study guides make Unit 8 AP Calc AB topics approachable and ensure you’re ready for any test question that comes your way.

Yes! Several platforms offer AP Calc AB Unit 8 practice tests, but not all provide the depth you need. For comprehensive preparation, focus on:

  • UWorld’s AP Calculus AB Unit 8 practice tests: Offer realistic exam conditions, detailed solutions, and difficulty matching the real AP exam.
  • College Board’s progress checks: Useful for official-style practice.
  • Free online quizzes: Good for quick reviews, but often lack explanation depth.

UWorld stands out because every question is followed by a clear, step-by-step explanation that connects the question to the underlying concept. You’ll also find AP Calc AB Unit 8 MCQ and FRQ sets that help you identify weak spots and improve your problem-solving process. Regularly practicing with UWorld ensures you not only remember formulas but also understand how and when to apply them—key to scoring higher on the actual test.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus AB by exploring related units that build on these concepts.
Unit 1

Limits and Continuity
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 4

Contextual Applications of Differentiation
Unit 5

Analytical Applications of Differentiation
Unit 6

Integration and Accumulation of Change
Unit 7

Differential Equations
Scroll to Top

Crack AP Calc AB

Get Exam Ready
In Less Time
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.