AP® Calculus AB Unit 7 Review and Practice Test
Get ready for your Unit 7 AP® Calculus AB test with our comprehensive Differential Equations review. This unit introduces slope fields, separable differential equations, and real-world modeling of motion and growth, core concepts that deepen your understanding of calculus.
Use our AP Calculus AB Unit 7 review to practice with exam-style MCQs, FRQs, and slope field problems that reflect what you’ll see on the AP Exam. This resource helps you connect ideas and build the confidence to score high.
Boost Your Confidence and Score High with Our AP Calculus AB Unit 7 Review
Master Unit 7 AP Calculus AB: Differential Equations with everything you need to succeed. This review covers slope fields, separable differential equations, and how to model growth and decay using derivatives. Practice with AP Calculus AB Unit 7 MCQs, FRQs, and progress check questions that mirror the real exam format. Strengthen your understanding with our step-by-step AP Calc AB Unit 7 study guide and interactive video lessons.
Engaging Video Lessons
Visualize how slope fields and separable differential equations work with UWorld’s engaging AP Calc AB Unit 7 video lessons. Each concept, whether it’s interpreting slope patterns, solving initial value problems, or modeling exponential growth—is broken down into simple, visual steps. These high-yield videos make challenging topics in Unit 7 AP Calculus AB easy to follow and remember, helping you build a strong foundation for your AP Calculus AB Unit 7 review.
Interactive Study Guides
Our AP Calculus AB Unit 7 study guide follows the College Board’s CED and simplifies key topics like slope fields, separable equations, and modeling with derivatives. Built-in checks for understanding help you test your knowledge as you progress, ensuring that each concept in AP Calc AB Unit 7, from differential equations to their graphical interpretations, is clear before you move ahead.
Try These AP Calculus AB Unit 7 Practice Test Questions
Question
If the population P(t) of microorganisms in an experiment changes linearly, where t is the time in hours, which of the following differential equations could model the rate of change in the number of microorganisms?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
If the growth of a quantity is linear, then the rate of growth of the quantity is constant.
Explanation
The rate of change of a linear function y is a differential equation of the form , where k is the slope of the line (a constant) and is the derivative of y with respect to time t.
It is given that the population of microorganisms P(t) at time t in the experiment changes linearly, so the rate of change of the population is constant. Eliminate all choices that include a variable.
The only choice that could model the rate of change in the number of microorganisms is .
(Choices B and C) and model linear rates of change. However, the rate of change of the population must be a constant value for the population to change linearly.
(Choice D) contains a quadratic expression, but the rate of change of a linear function must equal a constant.
Things to remember:
The rate of change of a linear function y is a differential equation of the form , where k is the slope of the line (a constant) and is the derivative of a function y with respect to time t.
Question
Which of the following is the solution and its domain for the differential equation with the initial condition ?
| A. for | |
| B. for | |
| C. for | |
| D. for |
Hint :
To find a particular solution to a separable differential equation, first separate the variables.
Explanation
To find a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and then use an initial condition to find the expression for y that includes the constant of integration.
First multiply the given differential equation by dx and y to separate the variables on opposite sides of the equation.
| Given differential equation | |
| Multiply both sides by dx and y |
Now integrate both sides of the equation to find the general solution to the differential equation.
| Integrals of resulting equation | |
| Integrate | |
| Combine constants of integration |
To find the value of C, plug in the initial condition y(2) = −2 and solve for C.
| General solution to differential equation | |
| Plug in y(2) = −2 | |
| Simplify | |
| Subtract 32 from both sides |
Substitute C = −30 into the general solution to the differential equation, and then solve for y to find the particular solution to the differential equation.
| General solution to differential equation | |
| Substitute C = −30 | |
| Multiply both sides by 2 | |
| Take square root of both sides |
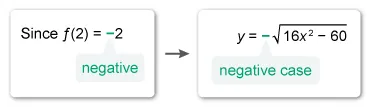
The equation represents two different solutions, and . Use the given initial condition to determine which case is the particular solution to the differential equation.
The y-value of the initial condition y(2) = −2 is negative, so the particular solution to the differential equation is the negative case . Eliminate Choices A and C.
There are only two possible domains given in the answer choices, and . Use the x-value of the initial condition (x = 2) to see that the domain must be because , so it is not necessary to derive the domain.
Therefore, the solution to the differential equation is and its domain is .
(Choice A) for may result from mistakenly using the x-value of the initial condition to choose the positive solution to the differential equation instead of the value of f(2).
(Choice C) for may result from the combination of errors described in Choices A and D.
(Choice D) for may result from mistakenly using the negative value of f(2), instead of the positive x-value, to determine the domain from the given condition.
Things to remember:
To determine a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and use the given initial condition to find the expression for f(x) that includes the constant of integration.
Question
If , and if y = 2 when x = 4, then y =
| A. 3 + e−x | |
| B. 3 − e−x | |
| C. 3 − e4 − x | |
| D. 3 − ex − 4 |
Hint :
To find a particular solution to a separable differential equation, separate the variables and integrate each side of the equation independently.
Explanation
To determine a particular solution to a separable differential equation, first separate the variables, integrate both sides of the equation, then add the constant of integration.
Multiply the differential equation by dx and divide by 3 − y to separate the variables.
Integrate both sides of the resulting equation independently. The left side is a composite function of the form , where u = 3 − y, so use u-substitution and the natural logarithm rule. Apply the power rule to the right side.
| Integral of both sides | |
| Substitute 3 − y = u and dy = −du | |
| Integrate | |
| Substitute u = 3 − y |
Plug in the given initial condition of x = 4 and y = 2 and solve for C to find the particular value of C.
| −ln|3 − y| = x + C | General solution to differential equation |
| −ln|3 − 2| = 4 + C | Plug in x = 4 and y = 2 |
| −ln|1| = 4 + C | Subtract |
| 0 = 4 + C | Simplify ln1 = 0 |
| −4 = C | Subtract 4 from both sides |
Substitute C = −4 into the general solution to the differential equation and solve for y.
| −ln|3 − y| = x + C | General solution to differential equation |
| −ln|3 − y| = x + (−4) | Substitute C = −4 |
| ln|3 − y| = 4 − x | Multiply both sides by −1 |
| |3 − y| = e4 − x | Apply logarithmic exponential relationship |
| 3 − y = ±e4 − x | Remove absolute value bars |
| 3 ± e4 − x = y | Solve for y |
The expression e4 − x is positive for all values of x and the given value of y = 2 is less than 3, so the exponential term must be negative.
Therefore, the solution to the given differential equation if y = 2 when x = 4 is y = 3 − e4 − x.
(Choices A and B) 3 + e−x and 3 − e−x may result from not adding a constant of integration when integrating both sides of the differential equation.
(Choice D) 3 − ex − 4 may result from not using u-substitution to integrate the y-term, leading to the incorrect integral .
Things to remember:
To determine a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and use the given initial condition to find the constant of integration.
It is also possible to find the solution to the given differential equation by using the given information to determine which choice satisfies the initial condition and differential equation.
First, plug the given value of x = 4 into each choice to verify which choices yield the given value of y = 2.
Eliminate Choices A and B because they do not yield values of y = 2 when x = 4.
Substitute each of the remaining choices in for y in the given differential equation to determine which results in a true statement.
Eliminate Choice D because it does not result in a true statement.
Therefore, the solution to the given differential equation if y = 2 when x = 4 is y = 3 − e4 − x.
Things to remember:
To find the particular solution to a differential equation given a finite number of choices, it may be possible to test each choice with given information to determine which satisfies the initial condition and differential equation.
Stand Out
with a Top Score in AP Calculus AB
Finish your AP Calculus AB Unit 7 review strong and keep building your mastery across all calculus units with UWorld. Earning a top score not only boosts your academic record but also enhances your eligibility for competitive college programs and scholarships.
Get our all-in-one course today!
- Focused AP Calc AB Videos
- Print & Digital Study Guide
- 1400+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What is AP Calculus AB Unit 7 about?
AP Calculus AB Unit 7, also called Differential Equations, focuses on understanding how derivatives describe patterns of change in real-world situations. Students learn to interpret and sketch slope fields, solve separable differential equations, and model growth and decay problems using initial conditions. This unit connects symbolic differentiation to graphical and numerical analysis, showing how solutions behave over time. Mastering unit 7 AP Calc AB concepts builds the foundation for motion, population, and rate-of-change modeling on the AP Exam.
UWorld’s AP Calc AB Unit 7 study guide explains each topic through clear visuals, annotated examples, and step-by-step reasoning that make complex differential ideas approachable. Our integrated platform lets you read the material, watch concise video lessons, and solve exam-style questions, all aligned with the College Board’s framework for AP Calculus AB unit 7 review.
Which topics are covered in AP Calculus AB Unit 7?
Unit 7 AP Calculus AB explores how differential equations describe real-world change and how graphical and analytical methods connect. This unit focuses on interpreting slope fields, solving separable differential equations, and understanding how solutions behave under given conditions. Each concept reinforces how derivatives, rates of change, and integration combine to form complete models of motion, growth, and decay.
Key topics include:
- Slope Fields: Visual representations of differential equations that show how solution curves behave across different regions.
- Separable Differential Equations: Techniques for separating variables and integrating to find general or particular solutions.
- Initial Value Problems: Applying initial conditions to determine specific solutions that fit given data.
- Exponential Growth and Decay Models: Using differential equations to describe population growth, radioactive decay, and other rate-based applications.
- Verifying Solutions: Checking work by differentiating and substituting into the original equation to confirm accuracy.
These topics require steady practice and conceptual understanding to master. UWorld’s AP Calculus AB Unit 7 review and study guide are aligned with the Course and Exam Description (CED), offering structured lessons and targeted AP Calc AB unit 7 practice tests. Each activity strengthens your grasp of unit 7 AP Calculus AB topics and builds exam confidence.
Where can I find the best AP Calculus AB Unit 7 study guide and notes?
An effective AP Calculus AB Unit 7 study guide connects concepts with application instead of treating them separately. UWorld’s print and digital AP Calc AB Unit 7 materials follow the College Board’s CED, covering every topic from slope fields and separable differential equations to initial value problems and growth models. Each section includes short comprehension checks so you can confirm mastery before moving on.
If you prefer digital materials, the AP Calculus AB Unit 7 notes PDF is available in the UWorld app, which also includes flashcards and a customizable study planner. You can start with a free trial to see how the platform combines reading, watching, and practicing in one place. This integrated system ensures your Unit 7 AP Calc AB review is efficient, engaging, and aligned with real exam requirements.
Where can I find AP Calculus AB Unit 7 practice tests with detailed answer explanations?
UWorld offers full-length AP Calculus AB Unit 7 practice tests that mirror the format and difficulty of the actual AP Exam. Each question is crafted to test your ability to interpret slope fields, solve separable differential equations, and apply initial conditions correctly. While the College Board provides sample FRQs and scoring guidelines, UWorld fills the gap for complete multiple-choice resources.
Every explanation walks you through step-by-step reasoning, why each answer is correct and why other options are not, helping you build deeper conceptual understanding. You can also create customized quizzes that focus on specific unit 7 AP Calculus AB topics such as exponential growth, decay, or motion. After each session, review the visuals and explanations to strengthen your problem-solving strategy. Regular practice with UWorld’s AP Calc AB Unit 7 review materials helps improve retention, accuracy, and pacing on test day.
What types of questions usually appear on the AP Calculus AB Unit 7 test?
Typical AP Calculus AB Unit 7 test questions assess your ability to analyze, interpret, and solve problems involving differential equations. You’ll encounter both multiple-choice (MCQ) and free-response (FRQ) formats that connect analytical, graphical, and contextual reasoning. Common question types include:
- Slope Field Analysis: Identify patterns in slope fields or match them to given differential equations.
- Separable Differential Equations: Separate variables, integrate, and apply constants or initial conditions.
- Exponential Growth and Decay: Model population, radioactive decay, or cooling scenarios using differential equations.
- Initial Value Problems: Solve for particular solutions using provided starting conditions.
- Verification and Interpretation: Differentiate to verify solutions and interpret what the derivative or solution represents.
UWorld’s AP Calc AB Unit 7 review includes MCQ and FRQ items modeled on the real exam, such as AP Calc AB slope field FRQ or AP Calc AB differential equations FRQ examples; with detailed visual explanations. Practicing these question types prepares you for every format on the unit 7 AP Calculus AB exam.
What are the AP Calculus AB Unit 7 concepts that students should master before the test?
Before your AP Calculus AB Unit 7 test, make sure you have a solid understanding of the core ideas behind differential equations and how they connect to real-world models. These concepts appear frequently on MCQ and FRQ questions in the AP Exam and require both algebraic fluency and conceptual reasoning. Key areas include:
- Understanding Slope Fields: Recognizing how slopes indicate the direction and steepness of solution curves.
- Solving Separable Differential Equations: Rearranging and integrating to find general and particular solutions.
- Applying Initial Value Problems: Using given data to find specific constants and interpret the resulting functions.
- Modeling Growth and Decay: Writing and solving equations for exponential models that describe population, motion, or cooling.
- Verifying Solutions: Checking accuracy by differentiating and substituting results into the original differential equation.
UWorld’s integrated study guide, concise videos, and flashcards make these concepts easier to master. Students who consistently read, watch, and practice with UWorld’s AP Calculus AB practice tests gain the confidence and accuracy needed to perform well on unit 7 AP Calc AB exams.
Are there any free resources available for AP Calculus AB Unit 7?
Yes. UWorld offers a free trial with access to selected AP Calculus AB Unit 7 practice tests and questions that focus on slope fields, differential equations, and initial value problems. Each question includes detailed, step-by-step explanations so you can see exactly how to set up, solve, and verify each type of problem.
Additionally, other free resources from platforms such as Khan Academy and the College Board can be paired with UWorld’s study tools to create a complete learning plan: the College Board outlines the exam structure and learning objectives, Khan Academy reinforces conceptual understanding, and UWorld’s AP Calc AB Unit 7 review materials refine application and test-taking skills.
Combining these resources ensures balanced preparation, helping you master every topic in unit 7 AP Calculus AB efficiently and perform with confidence on your exam.
How can I find an AP Calculus AB Unit 7 cheat sheet?
While a full study plan is always best, concise reference materials can help during last-minute review sessions. UWorld offers quick summaries and formula sheets that serve as an AP Calculus AB Unit 7 cheat sheet, highlighting key derivative concepts used in differential equations and slope fields. These resources include:
- Step-by-step methods for solving separable differential equations and applying initial conditions
- Common solution patterns for exponential growth and decay models
- Visual slope field examples that help connect equations to graphical behavior
- Integration formulas frequently used in unit 7 AP Calc AB topics
- Essential reminders on verifying solutions through differentiation
These summaries are available digitally through UWorld’s platform and can be used for quick review before quizzes or exams. Use them to reinforce your understanding of AP Calc AB Unit 7 concepts, but rely on full practice tests and problem walkthroughs for deeper mastery of analytical applications.
What are the best flashcards for AP Calculus AB Unit 7 review?
The most effective AP Calculus AB Unit 7 flashcards reinforce rules, formulas, and reasoning steps needed to solve differential equations efficiently. UWorld’s digital flashcards are built around active recall and spaced repetition so you can retain key relationships and methods for the exam. Each deck covers:
- Core vocabulary and ideas: slope field, differential equation, separable variables, initial value problem, and exponential growth or decay.
- Step-by-step setups for separating and integrating dy/dx expressions.
- Common integration patterns used in unit 7 AP Calc AB questions.
- Visual slope field prompts for interpreting direction and solution curves.
- Concept-check examples that link flashcards directly to related AP Calc AB Unit 7 practice tests.
UWorld’s adaptive flashcard system works across all devices, automatically repeating challenging concepts until you master them. You can tag problem types, monitor progress, and instantly connect each card to related practice questions, creating a seamless study routine for you.
How can I maximize my AP Calculus AB Unit 7 review?
A strong AP Calculus AB Unit 7 review blends reading, watching, and active problem-solving to ensure a complete understanding of differential equations and slope fields. UWorld combines all these study methods within one structured platform so you can prepare efficiently and confidently.
- Read: Begin with UWorld’s AP Calc AB Unit 7 study guide, which simplifies separable differential equations, initial value problems, and exponential growth and decay models using clear visuals and examples.
- Watch: Learn from high-yield video lessons that break down complex concepts, like slope field interpretation and verifying solutions, step by step.
- Practice: Reinforce your learning with AP Calculus AB Unit 7 practice tests that match the difficulty and question style of the actual exam, featuring both MCQs and FRQs.
- Active Recall & Spaced Repetition: Use UWorld’s flashcards to review problem-solving patterns and revisit key ideas at spaced intervals for long-term retention.
- Timed Practice: Simulate the real exam setting with unit 7 AP Calc AB test sessions to build pacing and accuracy.
- Targeted Review & Tracking: Analyze your performance using UWorld’s progress dashboard to identify weak areas, review them, and measure improvement as you continue your AP Calculus AB Unit 7 preparation.
UWorld’s integrated system helps you read, watch, and practice in one place, ensuring you move from concept review to confident performance on your unit 7 test and full AP Calculus AB exam.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Definition and Fundamental Properties
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Applications of Integration