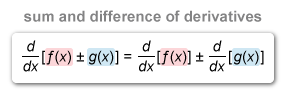AP Calculus AB Unit 2 Review and Practice Test
Prepare for your Unit 2 AP Calculus AB test with our complete Differentiation: Definition and Fundamental Properties review. This unit builds your understanding of what a derivative means and how to calculate it using various rules and formulas. You’ll explore the relationship between limits and slopes, understand how derivatives describe rates of change, and apply them to real-world and graphical problems. Our AP Calculus AB Unit 2 review combines high-yield video lessons, interactive study guides, and Unit 2 practice tests that mirror the actual AP exam format.
Boost Your Confidence and Score High with Our AP Calculus AB Unit 2 Review
Explore AP Calculus AB Unit 2: Differentiation: Definition and Fundamental Properties with everything you need to achieve success. This AP Calc AB Unit 2 review explains the limit definition of a derivative, core differentiation rules, and real-world applications involving rates of change. Strengthen your understanding with AP Calculus AB Unit 2 MCQs and practice tests that mirror the actual exam, and reinforce learning with UWorld’s detailed Unit 2 study guide and engaging video lessons.
Engaging Video Lessons
Learn how derivatives represent rates of change and slopes of tangent lines through clear, visual lessons. Our instructors walk you through the limit definition, derivative notation, and real-world applications such as motion and optimization. Each video focuses on AP Calculus AB Unit 2 skills like the power, product, quotient, and chain rules to build conceptual clarity and problem-solving accuracy.
Interactive Study Guides
Our AP Calculus AB Unit 2 study guide covers every topic in the College Board’s CED for Differentiation: Definition and Fundamental Properties. Built-in knowledge checks test your understanding of limits, derivative rules, and slopes so your AP Calculus AB Unit 2 review stays focused and effective.
Try These AP Calculus AB Unit 2 Practice Test Questions
Question
If
| A. | |
| B. | |
| C. | |
| D. nonexistent |
Hint :
A limit of the form is the definition of f '(a), the derivative of a function f(x) at x = a.
Explanation
A limit of the form is the definition of f '(a), the derivative of a function f(x) at x = a.
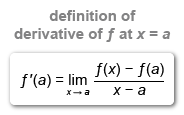
Usual limit evaluation techniques do not apply to a limit of this form, so identify the function f(x), the value of a, and then calculate f'(a) to evaluate the limit.
Compare the given limit to the definition of the derivative to identify f(x) and a, which is the x-value the limit is approaching.
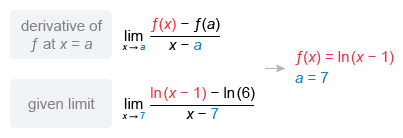
If a = 7, then ln(6) must equal f(7), ln(x - 1) must equal f(x), and must equal f'(7). Note: To verify that f(7) = ln(6), plug 7 into f(x) = ln(x - 1).
To evaluate f'(7), differentiate f(x) and then plug in x = 7. The function f(x) = \ln(x - 1) is a composite function, so use the chain rule to find f'(x).
| Given function | |
| Differentiate | |
| Multiply | |
| Plug in x = 7 | |
| Simplify |
Therefore, = .
(Choice A) 0 may result from attempting to evaluate the limit by direct substitution and assuming that the indeterminate form equals 0.
(Choice B) may result from not using u-substitution to integrate ln(x - 1).
(Choice D) "Nonexistent" may result from attempting to evaluate the limit by direct substitution and assuming that the indeterminate form does not exist.
Things to remember:
A limit of the form is the definition of f'(a), the derivative of a function f(x) at x = a.
Alternate Method :
An alternate way to evaluate the limit is to plug in x = 7 and try direct substitution.
| Given limit | |
| Plug in x = 7 | |
| Simplify |
Direct substitution yields the indeterminate form , so apply L'Hospital's Rule. Differentiate the numerator and denominator independently using derivative rules, and then try direct substitution on the resulting fraction.
The function ln(x-1) is a composite function, so use the chain rule to differentiate.
|
|
Equation from given limit |
|
|
Apply L'Hospital's Rule |
|
|
Differentiate |
|
|
Simplify and plug in x = 7 |
|
|
Subtract |
Therefore, = .
Things to remember:
- To evaluate a limit of the form first try directly substituting x = c into the function. If direct substitution yields the indeterminate form , simplify the expression or apply L'Hospital's Rule.
- To differentiate a composite function, use the chain rule:
Question
If , then f ′(x) =
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The derivative of the difference of two or more functions is equal to the difference of their derivatives.
Explanation
The derivative of the sum or difference of two or more functions is equal to the sum or difference of their derivatives.
The given function f(x) = 7 cot x - frac{3}{x^4} is a difference of two functions, so apply the sum and difference of derivatives property to find f'(x).
To differentiate f(x), first rewrite the second term in the form x−n. Then use differentiation rules to find f′(x).
| Result of sum and difference rule | |
| Rewrite | |
| Differentiate cot x and apply power rule | |
| Rewrite to match answer choices |
Therefore, the derivative of the given function f is
(Choice A) may result from incorrectly differentiating the first term using the derivative of csc x (instead of cot x) and not using the negative exponent rule when rewriting the second term.
(Choice B) may result from incorrectly differentiating the first term using the derivative of csc x and not including the negative sign.
(Choice C) may result from not including the negative sign in the derivative of cot x and mistakenly adding 1 (instead of subtracting 1) to the exponent when applying the power rule to the second term.
Things to remember:
The derivative of the difference of two or more functions is equal to the difference of their derivatives:
Question
What is the slope of the line tangent to the graph of at ?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The slope of the line tangent to a function at is the value of the derivative of at
Explanation
The slope of the line tangent to a function at is the value of the derivative of at
To determine the slope of the line tangent to at , first differentiate to find and then plug in The given function is the product of two functions, so use the product rule to differentiate:
Let and , and then differentiate both equations to find and
Now apply the product rule to find .
| Product rule | |
| Substitute , , , and | |
| Simplify |
To find the slope of the line tangent to at , plug into the equation for and evaluate the resulting expression.
|
Derivative of
|
|
| Plug in | |
| Evaluate and | |
| Simplify |
Therefore, the slope of the line tangent to the graph of at is .
(Choice B) may be the result of incorrectly calculating the values of the trigonometric functions at : and .
(Choice C) may be the result of mistakenly plugging into , rather than , to calculate the slope of the tangent line.
(Choice D) may be the result of subtracting, rather than adding, when using the product rule: .
Things to remember:
- The slope of the line tangent to a function is the value of the derivative of .
-
To find the derivative of the product of two functions, use the product rule:
Stand Out
with a Top Score in AP Calculus AB
Finish your AP Calculus AB Unit 2 review and continue mastering all units with UWorld. Boost your performance and make yourself a standout candidate for competitive colleges, majors, and scholarships by earning a top score.
Get our all-in-one course today!
- Focused AP Calc AB Videos
- Print & Digital Study Guide
- 1400+ Exam-style Practice Questions
- Customizable Quiz Generator
- Adjustable Study Planner
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Progress Dashboard
- Smart Flashcards & Digital Notebook
Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

The best part is that all options are well-explained, telling clearly why they are not the right option.
Frequently Asked Questions (FAQs)
What is AP Calculus AB Unit 2 about?
AP Calculus AB Unit 2, titled Differentiation: Definition and Fundamental Properties, introduces one of the most important concepts in calculus; the derivative. This unit explores how limits define the derivative, how it represents the slope of a tangent line, and how it can be used to describe instantaneous rates of change in various contexts. You’ll learn to apply the power, product, quotient, and chain rules to find derivatives of algebraic, trigonometric, exponential, and composite functions.
UWorld’s AP Calculus AB Unit 2 study guide provides comprehensive coverage of every topic with clear visuals, solved examples, and concise explanations that make challenging derivative concepts easier to grasp. Our integrated approach lets you read structured lessons, watch high-yield video explanations, and practice with AP Calculus AB Unit 2 practice tests that mirror real exam questions; all in one platform designed to strengthen understanding and boost confidence.
Which topics are covered in AP Calculus AB Unit 2?
Unit 2 AP Calculus AB, titled Differentiation: Definition and Fundamental Properties, focuses on how derivatives are defined and applied to understand change. This unit includes several core topics that form the foundation of calculus and prepare you for later units on applications of differentiation and curve analysis.
Key topics covered include:
- Definition of the Derivative: Understanding derivatives as limits of difference quotients and interpreting instantaneous rates of change.
- Derivative Rules: Applying the power, product, quotient, and chain rules to algebraic, trigonometric, exponential, and composite functions.
- Graphical and Analytical Interpretation: Identifying slopes of tangent lines, points of non-differentiability, and relationships between a function and its derivative graph.
- Real-World Applications: Using derivatives to analyze motion, velocity, acceleration, and related rates.
- Notation and Higher-Order Derivatives: Understanding derivative notation and extending it to higher orders for deeper problem solving.
These topics require active engagement and consistent reinforcement to master. UWorld’s QBank, aligned with the College Board’s CED, provides targeted AP Calculus AB Unit 2 practice test questions for each topic. You can generate customized quizzes on derivative practice or Unit 2 AP Calc AB concepts to strengthen weak areas and make your AP Calculus AB Unit 2 review efficient and results-driven.
Where can I find the best AP Calculus AB Unit 2 study guide and notes?
An effective AP Calculus AB Unit 2 study guide combines clear explanations with active learning so you can connect concepts to their applications. UWorld’s print and digital study guide for AP Calc AB Unit 2 covers every learning objective outlined in the College Board’s CED, including the definition of the derivative, differentiation rules, and graphical interpretations. Instead of simply reading through material, you’ll solve short derivative practice problems after each topic to strengthen understanding and retention. The guide features visual graphs, step-by-step examples, and concise explanations that simplify complex differentiation concepts.
If you prefer digital access, the AP Calculus AB Unit 2 PDF of notes is available through the UWorld app, which also stores flashcards, a customizable study planner, and performance tracking tools for flexible study sessions. UWorld also offers a free trial so you can explore how the AP Calculus AB Unit 2 study guide compares with other AP Calculus AB Unit 2 review materials and classroom notes. This integrated read–watch–practice approach helps you master topics efficiently and stay confident throughout your AP Calc AB Unit 2 test.
Where can I find AP Calculus AB Unit 2 practice tests with detailed answer explanations?
The College Board releases free-response questions (FRQs) with scoring guidelines but does not provide complete multiple-choice (MCQ) explanations. UWorld bridges that gap with a comprehensive AP Calculus AB Unit 2 practice test that includes both MCQs and FRQs modeled on the real exam. Each derivative practice problem features a detailed, line-by-line solution explaining how to set up, simplify, and solve using proper notation. This structure helps you learn not just the correct answer but the reasoning process that leads to it, essential for mastering Differentiation: Definition and Fundamental Properties.
UWorld’s platform lets you generate custom quizzes focused on Unit 2 AP Calc AB topics, from power-rule applications to chain-rule and product-rule combinations. Every question in the AP Calculus AB Unit 2 practice test with answers builds conceptual clarity and exam confidence through visual explanations and instant feedback. Regular practice strengthens recall and pacing, while performance analytics highlight areas to review. This targeted approach makes your AP Calculus AB Unit 2 review efficient, structured, and aligned with the actual exam format.
What types of questions usually appear on the AP Calculus AB Unit 2 test?
Typical AP Calculus AB Unit 2 test questions assess both conceptual understanding and procedural fluency in differentiation. Students are expected to demonstrate how derivatives describe change and apply rules accurately to solve a range of calculus problems. These questions often require algebraic manipulation, limit-based reasoning, and interpretation of graphs and tables.
Common Unit 2 AP Calculus AB question formats include:
- Multiple-Choice Questions (MCQs): Apply differentiation rules such as power, product, quotient, and chain to algebraic, trigonometric, and exponential functions.
- Graphical and Analytical Interpretation: Identify where functions are increasing or decreasing and determine slopes of tangent lines using derivatives.
- Contextual Applications: Solve rate-of-change, motion, and related-rate problems that require interpreting real-world scenarios using derivative formulas.
- Free-Response Questions (FRQs): Explain reasoning clearly while solving problems that combine analytical, graphical, and numerical representations.
- Derivative Practice Problems: Compute higher-order derivatives, evaluate limits defining derivatives, and justify solutions using calculus notation.
UWorld’s AP Calculus AB Unit 2 questions cover all these formats with detailed, visual explanations that guide you step-by-step through every problem. Because UWorld’s questions mirror the style and rigor of the actual AP Exam, when you read the lessons, watch the video walkthroughs, and practice using the AP Calculus AB Unit 2 practice test, you’ll gain complete familiarity with how real test questions are structured. UWorld’s AP Calc AB Unit 2 review materials ensure you’re fully prepared for any derivative-based question that might appear on the exam.
What AP Calculus AB Unit 2 concepts should students master before the test?
Before taking the AP Calculus AB Unit 2 test, students should have a solid grasp of foundational differentiation concepts that appear throughout the course and the AP Exam. This includes understanding both the definition and interpretation of derivatives, as well as the ability to apply various rules fluently across different types of functions.
Key concepts to master include:
- The limit definition of the derivative and its connection to instantaneous rate of change and tangent line slopes.
- Application of the power, product, quotient, and chain rules to polynomial, rational, trigonometric, and exponential functions.
- Recognizing points of non-differentiability and understanding their significance in graphs.
- Computing and interpreting higher-order derivatives to analyze motion, concavity, and acceleration.
- Solving real-world rate-of-change and motion problems using derivative equations.
- Interpreting derivative graphs to determine where functions are increasing, decreasing, or have extrema.
UWorld’s AP Calculus AB Unit 2 study guide, paired with its AP Calc AB Unit 2 review videos and derivative practice questions, provides structured explanations and visual examples that make each concept clear. Students who consistently read the material, watch UWorld’s short calculus lessons, and complete the AP Calculus AB Unit 2 practice test tend to feel more confident and perform better on both unit tests and the AP Exam.
Are there any free resources available for AP Calculus AB Unit 2?
Yes, UWorld offers a free trial that gives you access to AP Calculus AB Unit 2 practice test questions and derivative practice problems with detailed explanations and visual aids. This trial helps you explore the platform’s interactive study tools and understand how each question aligns with the AP Calculus AB Unit 2 review topics outlined by the College Board. You’ll see how every explanation connects core differentiation concepts, like power and chain rules, to real AP Exam-style problems.
To build a well-rounded study plan, you can also use free materials from the College Board and Khan Academy alongside UWorld’s resources. The College Board defines the course structure and exam format, Khan Academy supports conceptual learning, and UWorld refines your application and test-taking skills through structured practice. Using these together ensures your AP Calc AB Unit 2 preparation is balanced, efficient, and directly focused on mastering Differentiation: Definition and Fundamental Properties.
How can I find an AP Calculus AB Unit 2 cheat sheet?
While thorough study is always best, UWorld’s quick reference materials and summaries work as an effective AP Calculus AB Unit 2 cheat sheet for last-minute review. These concise resources highlight the essential concepts from Differentiation: Definition and Fundamental Properties and help reinforce what you’ve already practiced through the AP Calculus AB Unit 2 study guide and derivative practice questions.
Your Unit 2 AP Calc AB cheat sheet should include:
- Key derivative formulas, including the power, product, quotient, and chain rules
- The limit definition of the derivative and its connection to instantaneous rate of change
- Steps to find slopes of tangent lines and identify non-differentiable points
- Common differentiation errors and strategies to avoid them
- A list of derivative notations and what each represents
Remember, a calculus AB Unit 2 review or cheat sheet should supplement, not replace, comprehensive studying with UWorld’s full AP Calculus AB Unit 2 practice test and study tools. Use these summaries for quick refreshers, while relying on UWorld’s complete explanations and visuals to build lasting understanding and test confidence.
What are the best flashcards for AP Calculus AB Unit 2 review?
The most effective AP Calculus AB Unit 2 flashcards focus on reinforcing derivative rules, definitions, and real-world applications of differentiation. UWorld’s digital flashcards are designed for active recall and spaced repetition, helping students retain and apply key ideas from Differentiation: Definition and Fundamental Properties. Each deck connects conceptual understanding with step-by-step application, making it ideal for both daily practice and exam preparation.
Each AP Calc AB Unit 2 flashcard set covers:
- Core Vocabulary: Limit definition, derivative notation, slope of tangent, and rate of change.
- Differentiation Rules: Power, product, quotient, and chain rule formulas with example functions.
- Graphical Interpretation: Derivative graphs showing increasing/decreasing intervals and concavity.
- Applications: Motion, velocity, acceleration, and related rate problems.
- Common Errors: Misuse of rules or sign mistakes when differentiating composite functions.
UWorld’s AP Calculus AB Unit 2 study guide and flashcards work together to help you actively recall derivative concepts while connecting them to problem-solving strategies. This integrated system ensures your AP Calculus AB Unit 2 review is efficient, visual, and easy to reinforce across study sessions.
How can I maximize my AP Calculus AB Unit 2 review?
A strong AP Calculus AB Unit 2 review combines reading, watching, and active problem solving to build true understanding of differentiation. UWorld integrates all three study methods into one platform so you can master every topic in Differentiation: Definition and Fundamental Properties.
- Read: Start with UWorld’s AP Calculus AB Unit 2 study guide, which includes clear explanations and visual examples that simplify derivative definitions, rules, and real-world applications.
- Watch: Reinforce your understanding through short, high-yield video lessons that demonstrate how to apply derivative formulas, interpret graphs, and solve rate-of-change problems step-by-step.
- Practice: Strengthen your calculus skills with UWorld’s AP Calc AB Unit 2 practice test and derivative practice questions. Each includes detailed explanations that connect concepts to problem-solving techniques used on the AP Exam.
- Active Recall & Spaced Repetition: Use flashcards to review differentiation formulas and definitions at regular intervals to improve retention.
- Targeted Review & Tracking: Monitor your performance and focus on weaker topics using UWorld’s progress dashboard to ensure a balanced, results-driven study plan.
UWorld’s integrated approach ensures complete preparation, guiding you from concept mastery to confident performance on your AP Calculus AB Unit 2 test and the full AP Exam.
Learn More About Specific Unit
Limits and Continuity
Differentiation: Composite, Implicit, and Inverse Functions
Contextual Applications of Differentiation
Analytical Applications of Differentiation
Integration and Accumulation of Change
Differential Equations
Applications of Integration