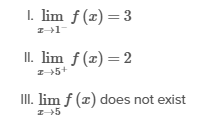Bundle 3+ College Prep products for 20% off

AP® Calculus AB Unit 1 Review and Practice Test

Limits and Continuity

Build a strong foundation in AP® Calculus AB Unit 1 with lessons on limits, continuity, and problem-solving. Practice with realistic MCQs and FRQs to boost confidence for your AP Calc AB exam.

AP Calculus AB prep course suite by UWorld

Excel in AP Calculus AB Unit 1: Limits and Continuity Review

Grasp key concepts from AP Calculus AB Unit 1 with focused lessons on limits and continuity. Utilize our Unit 1 AP Calculus AB review and practice problems to sharpen your skills and prepare for test day.

Watch

Engaging Video Lessons

Learn tricky AP Calculus AB Unit 1 concepts like limits, continuity, and one-sided limits through clear, step-by-step videos. Each lesson connects theory to real AP Calc AB Unit 1 test questions, helping you visualize and retain core ideas. Strengthen your understanding with engaging explanations that make complex topics easier to master.

Preview Video Lesson
Buy Now
UWorld’s AP Calc AB Video Lessons and Online Study Guide
UWorld’s AP Calculus AB Study Guide Prep book
Read

Interactive Study Guides

Explore AP Calculus AB Unit 1 study guides that simplify limits and continuity into clear, organized notes. Each section includes examples, visual aids, and AP Calc AB Unit 1 practice problems to reinforce learning. Use these interactive tools to review efficiently and prepare confidently for your next test.

Preview Book
Buy Now
Practice

Challenge Yourself with AP® Calculus AB Unit 1 Practice Questions

Test your understanding with AP Calculus AB Unit 1 practice test questions covering limits, continuity, and problem-solving strategies. Work through MCQs and FRQs similar to the Unit 1 progress check MCQ Part A and B. Each question includes detailed explanations to help you identify mistakes and master every concept before the exam.
Try these sample practice questions with detailed answer explanations:
Limits and Continuity Practice Tests

Question

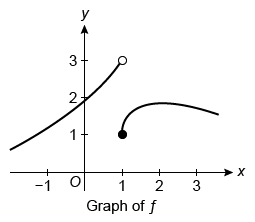
Graph of f

table of x and f(x)

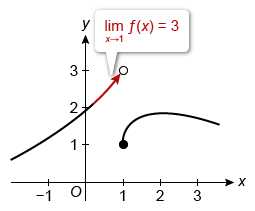
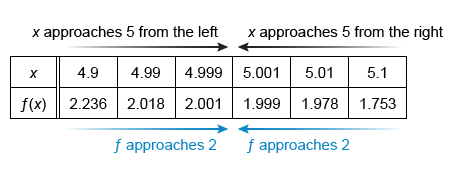
The function f is defined for all real values of x. The graph above shows the portion of the graph of f on [−1, 3], and the table above gives selected values of f near x = 5. Which of the following limit statements is likely to be true?

A. I and II only
B. I and III only
C. II and III only
D. I, II, and III

Explanation

As x approaches 1 from the left, the graph of f approaches 3. Therefore, lim x → 1 - f (x) = 3 and Statement I is true.

As x approaches 5 from the right, the values of f in the given table get very close to 2. Therefore, lim x → 5 + f (x) = 2 and Statement II is true.

As x approaches 5 from the left, the values of f in the given table also get very close to 2. Both limits of f approach the same value as x approaches 5, so lim x → 5 f (x) exists. Therefore, Statement III is false.

Question

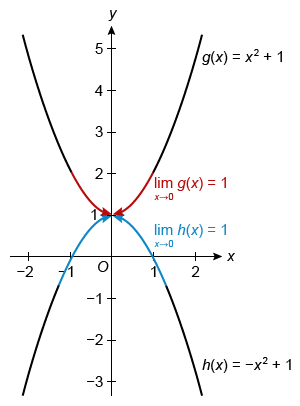
Let f, g, and h be functions such that g(x) ≤ f(x) ≤ h(x) for all values of x. Let g(x) = x2 + 1 and h(x) = −x2 + 1. At what value of x can the squeeze theorem be applied, and what is the limit of f as x approaches this value?

A. The squeeze theorem can be applied at x = 0 for the given functions, and lim x → 0 f (x) = 0 .
B. The squeeze theorem can be applied at x = 0 for the given functions, and lim x → 0 f (x) = 1 .
C. The squeeze theorem can be applied at x = 1 for the given functions, and lim x → 1 f (x) = 0 .
D. The squeeze theorem cannot be applied to the given functions.

Explanation

The functions g(x) = x2 + 1 and h(x) = −x2 + 1 only approach the same value as x approaches 0, so it is possible to apply the squeeze theorem at x = 0.

The limits of g and h as x approaches 0 are both 1, so the limit of f as x approaches 0 must equal 1.

indicating the graph

Question

lim x → 2 x 2 - 4 x - 2 =
A. 0
B. 2
C. 4
D. The limit does not exist.

Explanation

To evaluate the given limit, first try to substitute x = 2 into the limit directly.

Direct substitution yields an indeterminate form, so factor the numerator to evaluate.

Therefore, the given limit equals 4.

Buy Now
UWorld Dark Blue logo

Access Your AP® Calculus AB Review Anytime

Tackle AP Calculus AB Unit 1 practice questions on the go, review video lessons between classes, or study key concepts anytime with the UWorld app at your fingertips.

App Store
Google Play

Stand Out
with a Top Score in AP Calculus AB

Finish your AP Calculus AB Unit 1 review and continue mastering all units with UWorld. Boost your performance and make yourself a standout candidate for competitive colleges, majors, and scholarships by earning a top score.

Choose Your Subscription
Dream Score Plan
360-Day
$169
Deep Learning Plan
180-Day
$149
Score Booster Plan
90-Day (No print book, only digital)
$129
Introductory Plan
30-Day (No print book, only digital)
$99
Buy Now!

Get our all-in-one course today!

  • Focused AP Calc AB Videos
  • Print & Digital Study Guide
  • 1400+ Exam-style Practice Questions
  • Customizable Quiz Generator
  • Adjustable Study Planner
  • Realistic Timed Test Simulation
  • Colorful Visual Explanations
  • Progress Dashboard
  • Smart Flashcards & Digital Notebook
Explore our free trial and frequently asked questions.
7-Day Free Trial Subscription FAQs

Hear From Our AP Students

UWorld’s service is pretty good and helps provide a lot of explanations on subjects I haven’t been confident on before.

— Bence P.

The questions here are the most realistic to the AP tests I've seen so far! I appreciate the ability to customize tests as well.

— Kaila H.

The best part is that all options are well-explained, telling clearly why they are not the right option.

— Syeda Huma Z.
Read More Reviews

Frequently Asked Questions (FAQs)

AP Calculus AB Unit 1 focuses on understanding how functions behave as inputs approach specific values or infinity. Here’s a quick overview of the key topics:

  • How limits help us handle change at an instant: Learn how limits describe instantaneous change, forming the basis for derivatives.
  • Definition and properties of limits in various representations: Understand limits through tables, graphs, and equations to see how values approach a point.
  • Definitions of continuity of a function at a point and over a domain: Identify when a function is continuous and how to determine points of discontinuity.
  • Asymptotes and limits at infinity: Explore how functions behave as inputs grow large, and determine horizontal and vertical asymptotes.
  • Reasoning using the Squeeze Theorem and the Intermediate Value Theorem: Apply these theorems to estimate limits and prove the existence of values within intervals.

UWorld makes mastering these concepts easy through clear explanations, visual examples, and exam-style AP Calc AB Unit 1 practice questions that build strong problem-solving skills.

Preparing for your AP Calculus AB Unit 1: Limits and Continuity exam starts with building a strong understanding of fundamental concepts. Begin by reviewing your class notes and focusing on core ideas like evaluating limits, identifying points of discontinuity, and interpreting continuity on graphs and equations. Make sure you understand how to apply key theorems such as the Squeeze Theorem and Intermediate Value Theorem, since these often appear on both multiple-choice and free-response questions.

Once you’ve reviewed the content, shift your focus to practice. Solving AP-style questions is one of the best ways to test your comprehension and improve accuracy under timed conditions. UWorld’s AP Calculus AB Unit 1 practice questions are modeled after real exam problems and include detailed, step-by-step explanations for every solution, helping you understand not just what the correct answer is, but why.

You can also track your performance to identify weak areas and revisit related concepts through UWorld’s study guides and video lessons. Consistent practice with this combination of instruction, feedback, and self-assessment will help you retain key ideas, improve problem-solving speed, and feel confident heading into your AP Calc Unit 1 exam.

Yes! There are several free resources available to help you review AP® Calculus AB Unit 1: Limits and Continuity. The College Board’s AP Classroom offers topic questions and Unit 1 progress checks (MCQ Part A and Part B) to help you understand what to expect on the exam. Khan Academy also provides free instructional videos and practice problems to strengthen your understanding of limits, continuity, and related theorems.

However, if you want a true exam-level experience, UWorld is your best study companion. UWorld’s AP Calculus AB Unit 1 practice tests are designed by experts to mirror the real exam’s format and difficulty. Each question includes detailed explanations, visual aids, and answer rationales to help you understand concepts thoroughly, not just memorize formulas.

You can even start with UWorld’s free trial to explore interactive practice questions, detailed solutions, and performance tracking before committing to the full version.

While free tools offer a quick review, UWorld’s free trial lets you experience the most realistic and effective AP Calculus AB prep designed to boost your confidence and improve your score

The AP Calculus AB Unit 1 test includes both multiple-choice questions (MCQs) and free-response questions (FRQs) designed to test your understanding of limits and continuity in various contexts. You’ll encounter problems that ask you to:

  • Evaluate limits numerically, graphically, and algebraically
  • Determine points of discontinuity and explain whether a function is continuous
  • Apply the Squeeze Theorem and Intermediate Value Theorem to justify reasoning
  • Analyze functions involving asymptotes and limits at infinity

The MCQs often test conceptual understanding and quick application, while FRQs focus on clear mathematical reasoning and showing all steps.

UWorld’s AP Calculus AB Unit 1 practice tests mirror these exact question types, giving you realistic exam-style practice. Each question includes detailed explanations and visual breakdowns to help you understand the “why” behind each solution. By practicing with UWorld, you’ll strengthen both accuracy and confidence, ensuring you’re fully prepared for any question the AP exam presents.

To improve your score on the AP Calculus AB Unit 1 Free-Response Questions (FRQs), focus on clarity, accuracy, and reasoning. FRQs assess not just your final answer but how well you communicate your mathematical thinking. Start by reviewing common Unit 1 topics—limits, continuity, asymptotes, and theorems like the Intermediate Value Theorem (IVT) as these frequently appear in open-ended problems.

Here’s how to strengthen your FRQ performance:

  • Show every step clearly: Even if your final answer is off, partial credit is often awarded for correct reasoning and setup.
  • Use correct mathematical notation: Proper symbols and terminology make your solutions easier to follow and score higher.
  • Practice with real AP-style problems: UWorld offers AP Calculus AB Unit 1 FRQs that simulate exam conditions, complete with step-by-step solutions and scoring insights.
  • Review feedback and patterns: UWorld’s explanations highlight where mistakes happen and how to avoid them on test day.

By regularly solving UWorld’s FRQs, you’ll develop confidence in structuring answers, improve time management, and maximize points on this challenging section of the exam.

The “Limits and Continuity” unit makes up about 10–12% of the AP Calculus AB exam. While this may seem like a small portion, it’s one of the most important sections because it forms the foundation for nearly every topic that follows, especially derivatives and integrals.

Mastering AP Calc AB Unit 1 helps you understand how functions behave, change, and approach specific values, which is essential for success in later units. UWorld’s AP Calculus AB Unit 1 practice questions are designed to strengthen these core concepts through realistic problem sets, visual explanations, and instant feedback.

By consistently reviewing limits, continuity, and theorems like the Intermediate Value Theorem, you’ll not only secure points from this 10–12% but also build the confidence and understanding needed to excel throughout the rest of your AP Calculus AB course.

A great study guide for AP Calculus AB Unit 1: Limits and Continuity should include clear explanations, worked examples, and practice problems that match the AP exam format. While you can find summaries online or in textbooks, UWorld offers one of the most comprehensive and interactive study experiences.

UWorld’s AP Calculus AB Unit 1 study guide simplifies tough concepts like limits, continuity, and asymptotes through visual aids and concise explanations. Each topic is paired with AP-style questions and step-by-step solutions to reinforce learning and build problem-solving confidence. The guide also integrates review notes and progress check-style practice to mirror real exam conditions.

Unlike static notes or PDFs, UWorld’s study materials are dynamic and adaptive, helping you focus on weaker areas and retain key concepts longer. Whether you’re reviewing for a quiz or preparing for the AP exam, UWorld provides everything you need to study efficiently and confidently.

Yes, you can easily find practice tests that focus specifically on AP Calculus AB Unit 1: Limits and Continuity. Targeted practice helps you master early concepts before moving on to advanced topics.

  • UWorld’s AP Calculus AB Question Bank lets you filter and attempt Unit 1-specific quizzes. You’ll get realistic multiple-choice and free-response questions modeled after the actual AP exam.
  • Each question includes step-by-step explanations and visual aids, making it easier to understand challenging topics like limits from graphs, continuity, and the Squeeze Theorem.
  • You can also adjust difficulty levels, time yourself, and track progress to measure improvement over time.

Practicing with UWorld builds familiarity with real exam patterns and helps you identify weak areas early. It’s a smart, efficient way to strengthen your Unit 1 foundation and move into the rest of the course with confidence.

Learn More About Specific Unit

Strengthen your grasp of AP Calculus AB by exploring related units that build on these concepts.
Unit 2

Differentiation: Definition and Fundamental Properties
Unit 3

Differentiation: Composite, Implicit, and Inverse Functions
Unit 4

Contextual Applications of Differentiation
Unit 5

Analytical Applications of Differentiation
Unit 6

Integration and Accumulation of Change
Unit 7

Differential Equations
Unit 8

Applications of Integration
Scroll to Top

Crack AP Calc AB

Get Exam Ready
In Less Time
Start 7-Day Free Trial!
No Credit Card Required
See the UWorld Difference For Yourself

Frequently Asked Questions

New Purchase: All new subscriptions go into effect from the time they are activated and not at the time of setup/purchase. A subscription can be activated immediately or any time thereafter. If your initial purchase consists of multiple courses (Qbank, Self-Assessment exam, CCS, etc.), each can be activated individually and independently via your account on our website. This process of activating a subscription after purchase allows you the flexibility to start a subscription when you are truly ready to use it.

We recommend that all subscriptions be activated within 180 days of setup/purchase. Once a subscription is activated, it cannot be paused or suspended for any reason and will run continuously for the duration of the course material.

Renewal: A renewal is an extension of time to continue access to a current activated subscription. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the day of purchase and cannot be deferred to start at a later date/time.

Note: All of our subscriptions are based on the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Any of our product offerings can be purchased from our website with payment due in full at time of purchase via a credit or debit card with American Express/Discover/MasterCard or Visa logo.

You will need to register for an account in order to purchase any of our products. Once you have registered for an account or if you already have an account:

  • Log in to your UWorld account
  • Click on the Cart icon at the top of the page and then select your desired product to see a list of available packages and their prices
  • Select the package you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct product is in your cart and click Place Order
  • A purchase receipt will automatically be sent to your registered email address

If you complete your purchase but do not receive a receipt, please contact the Customer Care Team at [email protected]

You can subscribe to any of our online courses/services using a credit or debit card with a Visa, MasterCard, Discover or American Express logo. After a successful payment, your subscription will immediately be available for activation via your account on our website or available complementary mobile applications.

You can also subscribe via personal check, money order, or demand drafts taken in U.S. dollars. These types of payments should be mailed to us and should include the name of the subscription and the duration, along with the details asked for in the registration form. We will set up your account as soon as we receive your payment and notify you via email of your access credentials. All direct-mail payments must be in U.S. dollars and made payable to:

UWorld, LLC
9111 Cypress Waters Blvd
Suite 300
Dallas, TX 75019

We do not accept cash via mail, currencies other than U.S. dollars or payments via fax.

Individuals purchasing our CPA Review product may finance their purchase using Affirm during checkout process. Your eligibility depends on your credit score and other criteria, as per Affirm’s policies (outlined here). A soft credit check, a credit check that does not affect your credit score, will be performed by Affirm to determine your loan eligibility. You will need a US based bank account to qualify.

All refunds are evaluated on a case-by-case basis for products purchased directly from UWorld. One case has no bearing on another. Refund amounts determined by UWorld are final.

In-App Purchases: We are unable to process any refunds for purchases made via mobile application (in-app). Please contact Apple for all refund/credit requests for Apple in-app purchases.

USMLE Step 2 CS, Step 3 CCS, Subject Reviews & Self-Assessment Exams: These subscriptions are non-refundable, non-transferable, and cannot be converted into another subscription.

CPA Review: Students may request to cancel their CPA review product only within 10-days of activation of any of the materials. To qualify for a refund, no more than 10% of the course (lectures, Qbank, or a combination there-of) may have been used per exam section. All CPA Review refunds are subject to a cancellation fee of $75 (for single section purchases) or $250 (for package
purchases), plus any applicable shipping charges. No return of merchandise is necessary.

All other Qbanks: Refunds are considered for subscriptions of more than 30 days. Refund amounts are based on the number of days elapsed since the subscription start date or the number of questions used, whichever amounts to a higher deductible.

Example scenarion: An individual purchases a 180-day Qbank subscription and generates a few test blocks equal to 20% of the questions in the Qbank. After 45 days, he/she requests a refund. Because the elapsed duration is greater than the percentage of questions used, the refund amount will be based on a subscription converted to the closest duration (60 days) by deducting the applicable 60-day subscription fee from the refund. In the same scenario, if the individual had used 85% of the questions, the refund would be 15% of the subscription fee paid.

Note 1: A processing fee of 10% (minimum of $10 and maximum of $25) will be applied to all refund amounts.

Note 2: All refunds, pro-rated or otherwise, must be requested within 360 days of original purchase. Refunds for purchases made more than 360 days ago will be issued as non-refundable, non-transferable store credit.

Note 3: Subscribers must notify UWorld of their intent to obtain a refund before activating their subscription (or) during the active duration. If the reset option is used or all of the questions are used, no refund will be allowed (see “I want to reset/delete my Qbank test history (or) start all over again, is this possible?” below for further details). No refunds will be offered for expired subscriptions.

Note 4: For combination package purchases, individual subscription fees will be applied when calculating the refund. If any self-assessment Exam(s) is utilized from a package, the entire purchase is rendered non-refundable.

Note 5: Although access to Qbanks via certain mobile devices is provided as an additional feature, it is not intended to be a replacement for computer access, and no refunds or cancellations will be honored due to user inability to install and/or use the provided software on any mobile device (regardless of whether the device meets the minimum system requirements).

Please use the following steps to purchase a renewal for your subscription:

  • Log in to your account on our website
  • Click on the User Icon in the top right corner of the screen
  • Click on the Renew button corresponding to your subscription
  • Select the Renewal duration you wish to purchase
  • Verify your profile information, address, and educational status, then click the Update button
  • Enter your Billing address and credit/debit card information, then click Review Order
  • Verify that the correct package is in your cart and click Place Order

Upon a successful transaction, you will be sent a confirmation email receipt.

A renewal is an extension of time to continue accessing an active subscription, and it will not start the subscription over, provide a reset, or grant access to additional questions that were not previously accessible. Because a renewal is an extension to an already active subscription, it is effective from the existing expiration date, not from the date of purchase, and cannot be deferred in any way to start at a later date/time.

Please note that to qualify for renewal pricing, you will need to renew the course before it expires. Renewals are not offered to expired subscriptions. If you fail to secure a renewal before the expiration date, you will need to purchase a new subscription at the regular price directly from our website to regain access to the material.

Note: All times and dates displayed for subscription expiration correspond with the Eastern Time Zone (GMT/UTC -5 hours or New York Time), which may be different than your local time zone.

Note: If your initial purchase was a combination package, you will need to renew each active subscription individually. You do not need to renew a course that has not been activated.

You may request to upgrade or downgrade your subscription purchase as long as it has not been activated. If you purchase a combination package, all included subscriptions must be unused. Please be advised that current subscription pricing will apply.

If your subscription has been activated, unfortunately, we cannot upgrade it retroactively. If seeking to downgrade, please refer to our refund policy for available options.

We do not offer custom duration(s) or combination packages other than those outlined on the website. Please refer to our purchase page for currently available subscriptions (including discounted combination packages for some products).

Self-Assessment exam subscriptions are for 14 days each. Subscribers whose active subscription(s) have not expired can purchase renewals from 7 days or more at any time before their active subscription expires. Please refer to the respective course description page for renewal options.

We offer a demo on each of our product pages that contains a sample of the product interface and a few sample questions. We do not offer guest/trial accounts to test our software and view materials.

It is possible to purchase a subscription as a gift for someone else. However, the intended recipient will need to register an account on our website (or have an account registered for them, with their profile information entered accurately). If the user is present at the time of purchase, the purchase can be made from their account on our website using any credit or debit card with a Visa, MasterCard, American Express, or Discover logo.

If the user is not present, or you wish for the gift to be a surprise, please contact Support directly using the contact form to arrange payment for the gift subscription. You will need to provide the user’s registered email address so the account can be located.