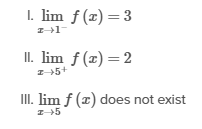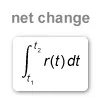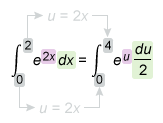AP® Calculus AB Practice Tests & Questions
Ace AP® Calculus AB with practice test questions from our Question Bank (QBank) and earn college credit on your schedule and budget.
Access Includes
- 1400+ Exam-style Practice Questions
- Customizable Quiz Generator
- Realistic Timed Test Simulation
- Colorful Visual Explanations
- Step-by-Step Solutions
- Adjustable Smart Study Planner
- Progress Dashboard
- Smart Flashcards
Try These AP Calc AB Practice Test Questions
Limits and Continuity Practice Test
Question
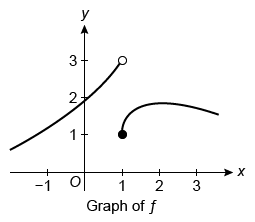
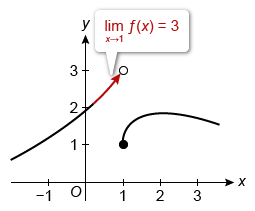
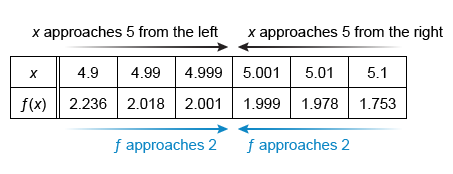
The function f is defined for all real values of x. The graph above shows the portion of the graph of f on [−1, 3], and the table above gives selected values of f near x = 5. Which of the following limit statements is likely to be true?
| A. I and II only | |
| B. I and III only | |
| C. II and III only | |
| D. I, II, and III |
Explanation
As x approaches 1 from the left, the graph of f approaches 3. Therefore, and Statement I is true.
As x approaches 5 from the right, the values of f in the given table get very close to 2. Therefore, and Statement II is true.
As x approaches 5 from the left, the values of f in the given table also get very close to 2. Both limits of f approach the same value as x approaches 5, so exists. Therefore, Statement III is false.
Question
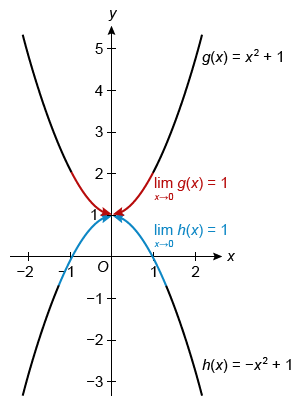
Let f, g, and h be functions such that g(x) ≤ f(x) ≤ h(x) for all values of x. Let g(x) = x2 + 1 and h(x) = −x2 + 1. At what value of x can the squeeze theorem be applied, and what is the limit of f as x approaches this value?
| A. The squeeze theorem can be applied at x = 0 for the given functions, and . | |
| B. The squeeze theorem can be applied at x = 0 for the given functions, and . | |
| C. The squeeze theorem can be applied at x = 1 for the given functions, and . | |
| D. The squeeze theorem cannot be applied to the given functions. |
Differentiation: Definition and Fundamental Properties Practice Test
Question
If
| A. | |
| B. | |
| C. | |
| D. nonexistent |
Hint :
A limit of the form is the definition of f '(a), the derivative of a function f(x) at x = a.
Explanation
A limit of the form is the definition of f '(a), the derivative of a function f(x) at x = a.
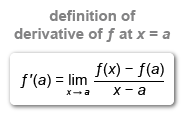
Usual limit evaluation techniques do not apply to a limit of this form, so identify the function f(x), the value of a, and then calculate f'(a) to evaluate the limit.
Compare the given limit to the definition of the derivative to identify f(x) and a, which is the x-value the limit is approaching.
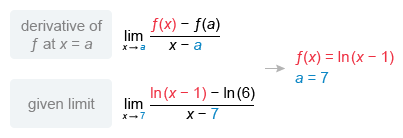
If a = 7, then ln(6) must equal f(7), ln(x - 1) must equal f(x), and must equal f'(7). Note: To verify that f(7) = ln(6), plug 7 into f(x) = ln(x - 1).
To evaluate f'(7), differentiate f(x) and then plug in x = 7. The function f(x) = \ln(x - 1) is a composite function, so use the chain rule to find f'(x).
| Given function | |
| Differentiate | |
| Multiply | |
| Plug in x = 7 | |
| Simplify |
Therefore, = .
(Choice A) 0 may result from attempting to evaluate the limit by direct substitution and assuming that the indeterminate form equals 0.
(Choice B) may result from not using u-substitution to integrate ln(x - 1).
(Choice D) "Nonexistent" may result from attempting to evaluate the limit by direct substitution and assuming that the indeterminate form does not exist.
Things to remember:
A limit of the form is the definition of f'(a), the derivative of a function f(x) at x = a.
Alternate Method :
An alternate way to evaluate the limit is to plug in x = 7 and try direct substitution.
| Given limit | |
| Plug in x = 7 | |
| Simplify |
Direct substitution yields the indeterminate form , so apply L'Hospital's Rule. Differentiate the numerator and denominator independently using derivative rules, and then try direct substitution on the resulting fraction.
The function ln(x-1) is a composite function, so use the chain rule to differentiate.
|
|
Equation from given limit |
|
|
Apply L'Hospital's Rule |
|
|
Differentiate |
|
|
Simplify and plug in x = 7 |
|
|
Subtract |
Therefore, = .
Things to remember:
- To evaluate a limit of the form first try directly substituting x = c into the function. If direct substitution yields the indeterminate form , simplify the expression or apply L'Hospital's Rule.
- To differentiate a composite function, use the chain rule:
Question
If , then f ′(x) =
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The derivative of the difference of two or more functions is equal to the difference of their derivatives.
Explanation
The derivative of the sum or difference of two or more functions is equal to the sum or difference of their derivatives.
The given function f(x) = 7 cot x - frac{3}{x^4} is a difference of two functions, so apply the sum and difference of derivatives property to find f'(x).
To differentiate f(x), first rewrite the second term in the form x−n. Then use differentiation rules to find f′(x).
| Result of sum and difference rule | |
| Rewrite | |
| Differentiate cot x and apply power rule | |
| Rewrite to match answer choices |
Therefore, the derivative of the given function f is
(Choice A) may result from incorrectly differentiating the first term using the derivative of csc x (instead of cot x) and not using the negative exponent rule when rewriting the second term.
(Choice B) may result from incorrectly differentiating the first term using the derivative of csc x and not including the negative sign.
(Choice C) may result from not including the negative sign in the derivative of cot x and mistakenly adding 1 (instead of subtracting 1) to the exponent when applying the power rule to the second term.
Things to remember:
The derivative of the difference of two or more functions is equal to the difference of their derivatives:
Question
What is the slope of the line tangent to the graph of at ?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The slope of the line tangent to a function at is the value of the derivative of at
Explanation
The slope of the line tangent to a function at is the value of the derivative of at
To determine the slope of the line tangent to at , first differentiate to find and then plug in The given function is the product of two functions, so use the product rule to differentiate:
Let and , and then differentiate both equations to find and

Now apply the product rule to find .
| Product rule | |
| Substitute , , , and | |
| Simplify |
To find the slope of the line tangent to at , plug into the equation for and evaluate the resulting expression.
| Derivative of |
|
| Plug in | |
| Evaluate and | |
| Simplify |
Therefore, the slope of the line tangent to the graph of at is .
(Choice B) may be the result of incorrectly calculating the values of the trigonometric functions at : and .
(Choice C) may be the result of mistakenly plugging into , rather than , to calculate the slope of the tangent line.
(Choice D) may be the result of subtracting, rather than adding, when using the product rule: .
Things to remember:
- The slope of the line tangent to a function is the value of the derivative of .
-
To find the derivative of the product of two functions, use the product rule:
Differentiation: Composite, Implicit, and Inverse Functions Practice Test
Question
If , then
| A. | |
| B. | |
| C. | |
| D. |
Hint :
Use the chain rule to differentiate a composite function.
Explanation
To find f ′(c), the value of the derivative of a function f at x = c, first differentiate f and then plug x = c into f ′(x).
The given function is a composite function of the form cos u, where is the inside function.
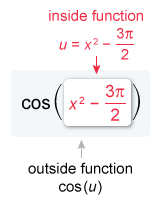
To find the derivative of a function of the form cos u, use the chain rule.
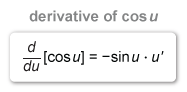
First differentiate the outside function with respect to the inside function, leaving the inside function intact. Then multiply by the derivative of the inside function with respect to x.
| Given function | |
| Apply chain rule | |
| Differentiate |
To evaluate , plug into and simplify the result.
| Derivative of | |
| Plug in | |
| Evaluate: | |
| Simplify: | |
| Evaluate: |
Therefore, .
(Choice A) may result from differentiating incorrectly: .
(Choice B) may result from not using the chain rule: .
(Choice C) may result from not using the chain rule: .
Things to remember:
To find the derivative of a composite function, use the chain rule:
Question
If , then
| A. 2 cos x − 3e3x | |
| B. −2 sin x − 9e3x | |
| C. −2 cos x − e3x | |
| D. −2 cos x − 27e3x |
Hint :
The notation represents the third derivative of y with respect to x.
Explanation
The notation represents the third derivative of y with respect to x. To find the third derivative:
Differentiate each term of the given function y = 2sinx − e3x to find the first derivative.
Use trigonometric differentiation rules to differentiate the first term. The second term is a composite function of the form eu where u = 3x, so use the exponential chain rule to differentiate.
| Given function | |
| Apply constant and trigonometric rules to differentiate first term | |
| Differentiate second term |
To find the second derivative, differentiate the first derivative.
| First derivative | |
| Apply constant and trigonometric rules to differentiate first term | |
| Apply constant and exponential rules to differentiate second term | |
| Simplify |
Now differentiate the second derivative to find the third derivative.
| Second derivative | |
| Apply constant and trigonometric rules to differentiate first term | |
| Apply constant and exponential rules to differentiate second term | |
| Simplify |
Therefore, the third derivative of y = 2 sin x − e3x is .
(Choice A) 2 cosx − 3e3x is the first derivative of 2sinx − e3x, but the question asks for the third derivative.
(Choice B) −2sinx − 9e3x is the second derivative of 2sinx − e3x, but the question asks for the third derivative.
(Choice C) may result from not applying the chain rule to differentiate the second term.
Things to remember:
- The notation represents the third derivative of y with respect to x.
- To find the derivative of a composite function, use the chain rule.
Question

The table above gives selected values for a differentiable and increasing function g and its derivative. If g−1 is the inverse function of g, what is the value of (g −1)′(4) ?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
If g−1 is the inverse of the function g, then the derivative of g−1 at the point (a, b) is the reciprocal of the derivative of g at the point (b, a).
Explanation
If g−1 is the inverse of the function g, then the derivative of g−1 at the point (a, b) is the reciprocal of the derivative of g at the point (b, a):
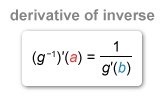
To find (g−1)′(4), first use the table to find the value of x for which g(x) = 4. The table shows that g contains the ordered pair (−1, 4), so it's inverse g−1 must contain the ordered pair (4, −1).
Plug a = 4 an b = −1 into the equation above, and then identify and plug in the value of gʹ(−1) from the given table.
| Derivative of the inverse of g | |
| Plug in a=4 and b=-1 | |
| Plug in g'(-1)=2 |
Therefore, the value of is .
(Choice A) is the value of , but the question asks for the value of .
(Choice B) is the value of , but the question asks for the value of .
(Choice D) result from mistakenly taking the negative reciprocal of , instead of the reciprocal of , to calculate .
Things to remember:
If g-1 is the inverse of the function g, then the derivative of g-1 at the point (a, b) is the reciprocal of the derivative of g at the point (b, a).
Contextual Applications of Differentiation Practice Test
Question
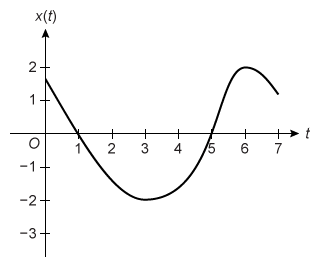
The graph above shows the position at time of a particle moving along a straight line for The graph has horizontal tangents at and and a point of inflection at . For what values of is the velocity of the particle decreasing?
| A. | |
| B. only | |
| C. and | |
| D. and |
Hint :
The velocity of a particle moving along a straight line is decreasing when
Explanation
To determine the interval(s) on which the velocity of a particle is decreasing from the graph of the position function, first recall that the velocity function v(t) is the derivative of the position function x(t).
If the velocity is decreasing, then the derivative of velocity v'(t) must be negative and therefore the second derivative of the position function x''(t) must also be negative.
The second derivative of a function determines the concavity of its graph. Since x''(t) < 0, identify where the graph of x(t) is concave down.
The graph of x(t) has a point of inflection at t = 5, so the graph changes concavity at that point.

The graph of x(t) is concave down on the interval 5 < t < 7, so the velocity is decreasing on 5 < t < 7 only.
(Choice A) 0 < t < 5 is the interval on which the velocity is increasing, but the question asks for the interval on which the velocity is decreasing.
(Choice C) 0 < t < 3 and 6 < t < 7 may be a result of identifying the intervals on which the velocity is negative rather than the interval on which the velocity is decreasing.
(Choice D) 0 < t < 1 and 5 < t < 7 may be a result of identifying intervals on which x(t) > 0 rather than on which the velocity is decreasing.
Things to remember:
To determine when the velocity of a function is decreasing from the graph of its position function, identify when the graph of x(t) is concave down.
Question
The volume of a cube with edges of length
| A. | |
| B. | |
| C. | |
| D. |
Hint :
To solve a related rates problem, first identify the rate to be found, the given rate, and any other given values.
Explanation
The rate at which a quantity changes is given by the derivative of that quantity with respect to time. To solve a related rates problem in which one rate is given and another rate is to be found, first identify the rate to be found, when it is to be found, and the given rate.

To find the rate at which x is changing with respect to time when , differentiate both sides of the volume equation with respect to time t. Then plug in the given values for and x and solve for .
| Volume of a cube with edge length x | |
| Differentiate both sides with respect to t: | |
| Plug in and | |
| Simplify right side: | |
| Divide both sides by | |
| Reduce: |
Therefore, is changing at the rate of centimeters per minute at the instant when .
(Choice B) may be a result of incorrectly differentiating the given expression for volume: .
(Choice C) may be a result of improperly differentiating the volume equation to get and solving for x rather than differentiating both sides of the volume equation with respect to t to get and solving for .
(Choice D)
Things to remember:
- To solve a related rates problem in which one rate is given and another rate is to be found, first identify the rate to be found, when it is to be found, and the given rate.
Question
is
| A. | |
| B. | |
| C. | |
| D. nonexistent |
Hint :
To evaluate a limit of the form , first directly substitute into the function.
Explanation
To evaluate a limit of the form , first directly substitute into the function and simplify. If the result yields an indeterminate form, apply L'Hospital's Rule.
| Given limit | |
| Plug in | |
| Evaluate: and |
Direct substitution results in the indeterminate form , so apply L'Hospital's Rule by differentiating the numerator and denominator independently, and then evaluate the limit again.
The numerator and denominator are composite functions of the form and , so use the chain rule to differentiate.
| Apply L'Hospital's Rule | |
| Differentiate numerator and differentiate denominator independently | |
| Evaluate limits of numerator and denominator | |
| Simplify |
Therefore, is −π.
(Choice B) 0 may result from assuming the indeterminate form = 0.
(Choice C) π may result from using an incorrect derivative:
(Choice D) "Nonexistent" may result from assuming that the indeterminate form means that the limit does not exist.
Things to remember:
- If a limit yields an indeterminate form, apply L'Hospital's Rule: Differentiate the numerator and denominator independently and then evaluate the limit.
Analytical Applications of Differentiation Practice Test
Question
The derivative of a continuous function f is given by for x > 0. If f(1) = 16 and f(4) = 19, what value of x in the open interval (1, 4) satisfies the conclusion of the Mean Value Theorem for f on the closed interval [1, 4] ?
| A. 1 | |
| B. | |
| C. | |
| D. 2 |
Hint :
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value in the interval (a, b).
Explanation
The Mean Value Theorem (MVT) guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change (AROC) of f on [a, b] for at least one x-value c in the interval (a, b).
To determine the value of x = c that satisfies the MVT for f on the closed interval [1, 4], first use the given function values to calculate the (AROC) of f(x) on [1, 4].
| AROC formula for a = 1 and b = 4 | |
| Plug in f(4) = 19 and f(1) = 16 | |
| Simplify |
The average rate of change of f(x) on [1, 4] is equal to 1, so set the given instantaneous rate of change equal to the average rate of change 1 and solve for x.
| Set instantaneous rate of change equal to AROC | |
| Multiply both sides by x2 | |
| Add 12 and subtract x2 on both sides | |
| Divide both sides by 3 | |
| Take the square root of both sides |
The solution x = −2 is not in the interval (1, 4), so the only value that satisfies the MVT for f on the closed interval [1, 4] is x = 2.
(Choice A) 1 is the value of the average rate of change of f on [1, 4], but the question asks for the value of x that satisfies the MVT on [1, 4].
(Choice B) may result from mistakenly setting f ′ equal to zero instead of setting f ′ equal to the average rate of change.
(Choice C) may result from incorrectly calculating the average rate of change as 3.
Things to remember:
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value in the interval (a, b).
Question
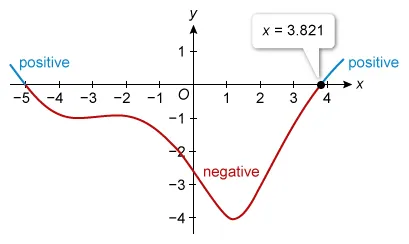
The function g is defined by . If the function f is an antiderivative of g, which of the following is the x-coordinate of the location of a local minimum for the graph of y = f(x) ?
| A. −5.058 | |
| B. −3.391 | |
| C. 1.216 | |
| D. 3.821 |
Hint :
An antiderivative f of a function g is any function whose derivative is g.
Explanation
An antiderivative f of a function g is any function whose derivative is g. It is given that f is an antiderivative of g, so the derivative of f is g.
A local (relative) minimum on the graph of f(x) occurs at any value of x where f′(x) = g(x) is zero or undefined (a critical point on the graph of f) and changes from negative to positive.
| To find the x-value of the relative minimum of f, graph its derivative and locate any zeros where the graph changes from negative to positive. |
The graph of f ′ = g changes from negative to positive at only one point, so the graph of y = f(x) has a relative minimum at x = 3.821.
(Choice A) −5.058 is the x-coordinate of a local maximum on the graph of f, but the question asks for the x-value of a local minimum.
(Choices B and C) −3.391 and 1.216 are x-coordinates of relative minimums on the graph of g(x), but the question asks for a relative minimum on the graph of f(x) = g ′(x).
Things to remember:
-
An antiderivative of a function f is any function F whose derivative is f.
-
A local minimum of a continuous function f(x) occurs at any value of x at which f ′(x) is zero or undefined and f ′ changes from negative to positive.
Question
The function f is continuous on the closed interval [−1, 5]. If f(−1) = −3 and f(5) = 3, which of the following conditions would guarantee that there is a number c in the open interval (−1, 5) where f ′(c) = 1 ?
| A. f is differentiable on the open interval (−1, 5). |
|
| B. f is not differentiable on the open interval (−1, 5). | |
| C. for all k on the open interval (−1, 5). | |
| D. f ′(k) = 0 for at least one value of k in the open interval (−1, 5). |
Hint :
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).
Explanation
The Mean Value Theorem (MVT) guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).
To guarantee there is a number c in the open interval (−1, 5) where f ′(c) = 1, first verify the average rate of change is 1 between the given points f(−1) = −3 and f(5) = 3 (calculation).
The MVT guarantees that f ′(c) = 1 if the MVT conditions are met for f on the interval [−1, 5]. It is given that f is continuous on [−1, 5], but no information is given about the differentiability of f on (1, 5).
The MVT applies to the continuous function f on [−1, 5] and guarantees that f ′(c) = 1 for at least one value of c in (−1, 5) only if f is differentiable on the open interval (−1, 5).
(Choice B) "f is not differentiable on the open interval (−1, 5)" indicates that the MVT does not apply to the function on the interval, but the question implies that the MVT does apply.
(Choice C) " for all k on the open interval (−1, 5)" indicates that the function is continuous on the open interval, but the MVT also requires differentiability.
(Choice D) "f ′(k) = 0 for at least one value of k in the open interval (−1, 5)" is the conclusion of Rolle's Theorem, but the question requires justifying the conditions of the MVT.
Things to remember:
The Mean Value Theorem guarantees that the instantaneous rate of change of a continuous and differentiable function f equals the average rate of change of f on [a, b] for at least one x-value c in the interval (a, b).
Integration and Accumulation of Change Practice Test
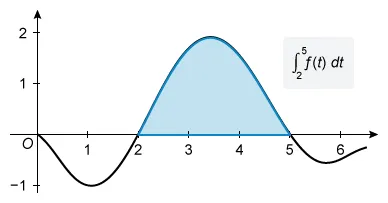
Question
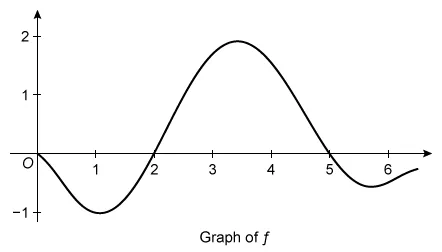
The graph of a differentiable function f is shown above. If , which of the following is true?
| A. g(5) < g′(5) < g″(5) | |
| B. g(5) < g″(5) < g′(5) | |
| C. g′(5) < g(5) < g″(5) | |
| D. g″(5) < g′(5) < g(5) |
Hint :
Determine whether each quantity is negative, zero, or positive and then compare their relative values.
Explanation
To compare the values of g(5), g′(5), and g″(5), evaluate g(5) and find the first and second derivatives of g(x) at x = 5.
Evaluate g(5)
Plug x = 5 into g(x) to evaluate g(5):
This definite integral represents the area bounded by the graph of f and the x-axis between x = 2 and x = 5. The exact value of g(5) cannot be determined, but this region is above the x-axis, so g(5) > 0.
Evaluate g′(5)
The given function is of the form , so use the Second Fundamental Theorem of Calculus (Second FTC) to differentiate g(x) and then plug in x = 5.
| Given function | |
| Differentiate both sides | |
| Apply Second FTC | |
| Plug in x = 5 |
Examine the graph of f at x = 5 to see that g′(5) = 0.
Evaluate g″(5)
Differentiate g′(x) = f(x) and then plug in x = 5 to evaluate g″(5).
| First derivative of | |
| Differentiate both sides | |
| Simplify | |
| Plug in x = 5 |
The value of is the slope of the line tangent to f at x = 5. The exact value of g″(5) cannot be found, but the slope of the tangent line is negative at x = 5, so g″(5) < 0.
Therefore, the statement g″(5) < g′(5) < g(5) is true because g″(5) < 0, g′(5) = 0, and g(5) > 0.
(Choice A)g(5) < g′(5) < g″(5) may result from mistakenly reversing the correct inequality.
(Choice B)g(5) < g″(5) < g′(5) may result from incorrectly calculating the relative values of the three quantities.
(Choice C)g′(5) < g(5) < g″(5) may result from assuming the graph represents g(x) rather than f(x).
Things to remember:
The derivative of an integral of the form , where f is a continuous function, is f(x):
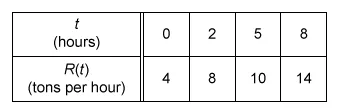
Question
The rate at which gravel is deposited at a landfill on a certain day is modeled by the function R, where R(t) is measured in tons per hour and t is the number of hours since the landfill opened. Using a trapezoidal sum with three subintervals as indicated by the data in the table above, approximate the number of tons of gravel deposited during the first 8 hours since the landfill opened.
| A. 75 | |
| B. 81 | |
| C. 128 | |
| D. 150 |
Hint :
The net change in a quantity over an interval of time is equal to the definite integral of the rate of change in the quantity over that interval.
Explanation
The number of tons of gravel deposited during the first 8 hours since the landfill opened is the net change in tons of gravel deposited at the rate R(t) from t1 = 0 to t2 = 8.
The net change in a quantity over an interval of time [t1, t2] is equal to the definite integral of the rate of change r(t) in the quantity over that interval.
Therefore, the number of tons of gravel deposited during the first 8 hours since the landfill opened is equal to .
To approximate the net change integral using a trapezoidal sum with three subintervals, calculate the areas of three trapezoids, where the trapezoid on subinterval n has height hn and base lengths bn and bn+1.
The height hn of each trapezoid is the length of the subinterval (distance between the t-values). The base lengths bn and bn+1 of each trapezoid are the values of R(t) at the endpoints of the subinterval.
The three subintervals from the given table are [0, 2], [2, 5], and [5, 8], so the heights of the trapezoids are 2, 3, and 3, respectively. The base lengths are the given values of R at the endpoints.
Plug values of bn and h for the three trapezoids into the trapezoidal sum expression and simplify. Factor the greatest common factor (GCF) out of the trapezoidal sum expression for a more efficient calculation.
| Trapezoidal sum | |
| . | Factor out GCF |
| Plug in values of bn and hn | |
| Simplify inside brackets | |
| 75 | Simplify |
Therefore, the approximate number of tons of gravel deposited during the first 8 hours since the landfill opened is 75.
(Choice B) 81 may result from mistakenly assuming that each of the three trapezoids has the same height (3).
(Choice C) 128 may result from approximating the number of tons of gravel using a left Riemann sum, but the question asks for the approximation using a trapezoidal sum.
(Choice D) 150 may result from neglecting the factors of in the trapezoidal sum equation.
Things to remember:
- The net change in a quantity over an interval of time [t1, t2] is given by the definite integral of the rate of change r(t) in the quantity from t1 to t2.
- A trapezoidal sum approximates a definite integral using trapezoids with height hn and base lengths bn and bn+1 to estimate the area under f in each subinterval.
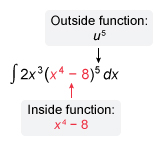
Question
| A. | |
| B. | |
| C. | |
| D. |
Hint :
If one factor of an integrand is a constant multiple of the derivative of the inside of a composite function, use -substitution to integrate.
Explanation
If one term of the integrand is a constant multiple of the derivative of the inside of a composite function, use -substitution to integrate.
.The given integrand contains the composite function , where is the inside function.
Check to see if the factor 2x3 from the integrand is a constant multiple of the derivative of x4−8 .
Since is a constant multiple of , use u-substitution to rewrite the integral in terms of u, where u=x4−8 , First differentiate u with respect to x, and then solve for dx.
| Inside function | |
| Differentiate both sides with respect to | |
| Multiply both sides by | |
| Divide both sides by to solve for |
Now substitute u for and for dx into the given integral, and then simplify and integrate.
| Given integral | |
| Substitute and | |
| Reduce: and apply: | |
| Reduce: | |
| Apply: | |
| Simplify |
Substitute back in for u to write the answer in terms of x .
| Answer in terms of | |
| Substitute back in for | |
| Rewrite to match answer choice |
Therefore, .
(Choice A) is a result of integrating each factor independently instead of using -substitution.
(Choice C) may be a result of omitting when substituting in for .
(Choice D) may be a result of mistakenly rewriting as .
Things to remember:
If one term of the integrand is a constant multiple of the derivative of the inside function of a composite function, use u-substitution to integrate.
Differential Equations Practice Test
Question
If the population P(t) of microorganisms in an experiment changes linearly, where t is the time in hours, which of the following differential equations could model the rate of change in the number of microorganisms?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
If the growth of a quantity is linear, then the rate of growth of the quantity is constant.
Explanation
The rate of change of a linear function y is a differential equation of the form , where k is the slope of the line (a constant) and is the derivative of y with respect to time t.
It is given that the population of microorganisms P(t) at time t in the experiment changes linearly, so the rate of change of the population is constant. Eliminate all choices that include a variable.
The only choice that could model the rate of change in the number of microorganisms is .
(Choices B and C) and model linear rates of change. However, the rate of change of the population must be a constant value for the population to change linearly.
(Choice D) contains a quadratic expression, but the rate of change of a linear function must equal a constant.
Things to remember:
The rate of change of a linear function y is a differential equation of the form , where k is the slope of the line (a constant) and is the derivative of a function y with respect to time t.
Question
Which of the following is the solution and its domain for the differential equation with the initial condition ?
| A. for | |
| B. for | |
| C. for | |
| D. for |
Hint :
To find a particular solution to a separable differential equation, first separate the variables.
Explanation
To find a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and then use an initial condition to find the expression for y that includes the constant of integration.
First multiply the given differential equation by dx and y to separate the variables on opposite sides of the equation.
| Given differential equation | |
| Multiply both sides by dx and y |
Now integrate both sides of the equation to find the general solution to the differential equation.
| Integrals of resulting equation | |
| Integrate | |
| Combine constants of integration |
To find the value of C, plug in the initial condition y(2) = −2 and solve for C.
| General solution to differential equation | |
| Plug in y(2) = −2 | |
| Simplify | |
| Subtract 32 from both sides |
Substitute C = −30 into the general solution to the differential equation, and then solve for y to find the particular solution to the differential equation.
| General solution to differential equation | |
| Substitute C = −30 | |
| Multiply both sides by 2 | |
| Take square root of both sides |
The equation represents two different solutions, and . Use the given initial condition to determine which case is the particular solution to the differential equation.
The y-value of the initial condition y(2) = −2 is negative, so the particular solution to the differential equation is the negative case . Eliminate Choices A and C.
There are only two possible domains given in the answer choices, and . Use the x-value of the initial condition (x = 2) to see that the domain must be because , so it is not necessary to derive the domain.
Therefore, the solution to the differential equation is and its domain is .
(Choice A) for may result from mistakenly using the x-value of the initial condition to choose the positive solution to the differential equation instead of the value of f(2).
(Choice C) for may result from the combination of errors described in Choices A and D.
(Choice D) for may result from mistakenly using the negative value of f(2), instead of the positive x-value, to determine the domain from the given condition.
Things to remember:
To determine a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and use the given initial condition to find the expression for f(x) that includes the constant of integration.
Question
If , and if y = 2 when x = 4, then y =
| A. 3 + e−x | |
| B. 3 − e−x | |
| C. 3 − e4 − x | |
| D. 3 − ex − 4 |
Hint :
To find a particular solution to a separable differential equation, separate the variables and integrate each side of the equation independently.
Explanation
To determine a particular solution to a separable differential equation, first separate the variables, integrate both sides of the equation, then add the constant of integration.
Multiply the differential equation by dx and divide by 3 − y to separate the variables.
Integrate both sides of the resulting equation independently. The left side is a composite function of the form , where u = 3 − y, so use u-substitution and the natural logarithm rule. Apply the power rule to the right side.
| Integral of both sides | |
| Substitute 3 − y = u and dy = −du | |
| Integrate | |
| Substitute u = 3 − y |
Plug in the given initial condition of x = 4 and y = 2 and solve for C to find the particular value of C.
| −ln|3 − y| = x + C | General solution to differential equation |
| −ln|3 − 2| = 4 + C | Plug in x = 4 and y = 2 |
| −ln|1| = 4 + C | Subtract |
| 0 = 4 + C | Simplify ln1 = 0 |
| −4 = C | Subtract 4 from both sides |
Substitute C = −4 into the general solution to the differential equation and solve for y.
| −ln|3 − y| = x + C | General solution to differential equation |
| −ln|3 − y| = x + (−4) | Substitute C = −4 |
| ln|3 − y| = 4 − x | Multiply both sides by −1 |
| |3 − y| = e4 − x | Apply logarithmic exponential relationship |
| 3 − y = ±e4 − x | Remove absolute value bars |
| 3 ± e4 − x = y | Solve for y |
The expression e4 − x is positive for all values of x and the given value of y = 2 is less than 3, so the exponential term must be negative.
Therefore, the solution to the given differential equation if y = 2 when x = 4 is y = 3 − e4 − x.
(Choices A and B) 3 + e−x and 3 − e−x may result from not adding a constant of integration when integrating both sides of the differential equation.
(Choice D) 3 − ex − 4 may result from not using u-substitution to integrate the y-term, leading to the incorrect integral .
Things to remember:
To determine a particular solution to a separable differential equation, separate the variables, integrate both sides of the equation, and use the given initial condition to find the constant of integration.
It is also possible to find the solution to the given differential equation by using the given information to determine which choice satisfies the initial condition and differential equation.
First, plug the given value of x = 4 into each choice to verify which choices yield the given value of y = 2.
Eliminate Choices A and B because they do not yield values of y = 2 when x = 4.
Substitute each of the remaining choices in for y in the given differential equation to determine which results in a true statement.
Eliminate Choice D because it does not result in a true statement.
Therefore, the solution to the given differential equation if y = 2 when x = 4 is y = 3 − e4 − x.
Things to remember:
To find the particular solution to a differential equation given a finite number of choices, it may be possible to test each choice with given information to determine which satisfies the initial condition and differential equation.
Applications of Integration Practice Test
Question
Rain is falling at the rate of inches per hour, where t is the time in hours since the rain began to fall. Which of the following gives the amount of rain, in inches, that falls from time to time hours?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The definite integral of a rate of change of a quantity over an interval gives the amount of change in the quantity over the interval.
Explanation
The definite integral of a rate of change r(t) of a quantity over an interval of time from t1 to t2 gives the amount of change in the quantity over the interval.
= amount of change (net change) in quantity from t1 to t2
Since is the rate of change of the rainfall, the amount of rain that falls between times t1=0 and t2=6 is given by
The integrand above is a composite function of the form where u = −0.2t is the inside function, so use u -substitution to integrate.
First differentiate u = −0.2t with respect to t to find dt in terms of u .
| Equation for | |
| Differentiate both sides with respect to t | |
| Multiply both sides by dt | |
| Divide both sides by −0.2 |
Calculate the limits of integration in terms of u and then substitute , , and the new limits of integration into the integral.
Now use the Fundamental Theorem of Calculus (FTC) to evaluate the resulting integral.
| Integral for amount of rain in terms of u | |
| Constant multiple rule: | |
| Simplify: | |
| Integrate: | |
| Apply the FTC | |
| Simplify: Rearrange terms to match answer choice |
Therefore, the amount of rain in inches that falls from time t=0 to time t=6 hours is given by
(Choice A) may be a result of neglecting to integrate the function or incorrectly integrating before applying the Fundamental Theorem of Calculus. This value is negative, which is not a valid option for the context of the question.
(Choice A) may be a result of differentiating rather than integrating the function before applying the Fundamental Theorem of Calculus.
(Choice C) may be a result of neglecting to integrate the function or incorrectly integrating before applying the Fundamental Theorem of Calculus and then incorrectly applying the Fundamental Theorem of Calculus:
Things to remember:
The definite integral of a rate of change of a quantity over
an interval gives the amount of change in the quantity over the interval.
Question
The base of a solid is the region in the first quadrant bounded by the graph of y = ex, the vertical line x = 2, and the x- and y-axes. For this solid, each cross section perpendicular to the x-axis is a square. What is the volume of the solid?
| A. | |
| B. | |
| C. | |
| D. |
Hint :
The volume of a solid with cross sections of area A(x) perpendicular to the x-axis is given by
Explanation
The volume of a solid with cross sections of area A(x) perpendicular to the x-axis is given by a definite integral of A(x) in terms of x.

Sketch the given boundaries of the region defined by the function y = ex, the line x = 2, and the x- and y-axes that form the base of the solid and determine the limits of integration.
The enclosed region spans the interval 0 ≤ x ≤ 2, so the limits of integration are x1 = 0 and x2 = 2.
The cross sections are squares, so A(x) = s2 is the integrand.
The side length s of each cross section is the vertical distance between the top and bottom functions, so s = top − bottom. Substitute y = ex for the top and y = 0 for the bottom and simplify.
To find an expression for the area function , plug into the formula for the area of a square to get . Substitute , , and into the volume integral to get .
The integrand is a composite function of the form , where , so rewrite the integral in terms of u. The derivative of is , so solve for . Plug the limits of integration for in to get 0 and 4.
Apply the constant multiple rule to rewrite the resulting integral as , then integrate and apply the Fundamental Theorem of Calculus (FTC).
| V = 1/2 ∫04 eu du | Resulting integral |
| V = 1/2 [ eu ]04 | Integrate |
| V = 1/2 ( e4 − e0 ) | Apply FTC |
| V = 1/2 e4 − 1/2 | Simplify e0 = 1 and distribute 1/2 |
Therefore, the volume of the solid is .
(Choice A) may result from not squaring the side length in the formula for the area of a square.
(Choice C)
may result from not integrating with
(Choice D)
may result from finding an incorrect expression of
(instead of
)
when applying
The volume of a solid with cross sections of area perpendicular to the x-axis is given by .
Question
What is the area of the region R bounded by the graphs of x = y2 − y + 1 and x = y + 1 ?
| A. | |
| B. | |
| C. 4 | |
| D. |
Explanation
The area between the given functions is equal to the integral of the right function minus the left function between the y-values of their intersection points, so it is necessary to determine which are the right and left functions and to find the intersection points.
The quadratic function has a positive leading coefficient, so the parabola opens to the right. All the choices are finite values, so the linear function must cross to the right of the quadratic (graph). Set the expressions equal and solve for y to find where they intersect.
| y2 − y + 1 = y + 1 | Set functions equal |
| y2 − 2y = 0 | Subtract y and 1 from both sides |
| y(y − 2) = 0 | Factor out GCF |
| y = 0 and y = 2 | Apply zero product property |
Therefore, the right function is f(y) = y + 1 and the left function is g(y) = y2 − y + 1, and they intersect at y = 0 and y = 2.
Integrate the difference between the functions on the interval of their intersection points to find the area of region R.
Therefore, the area of region R is .
Make the AP Calculus AB Exam Feel Like Practice
Our AP Calculus AB practice tests and quizzes are just like the exam and make you think critically. They’ll teach you to spot trick answers, handle time pressure and boost your confidence for test day! Practice with realistic exam simulations so test day feels like just another practice run.
One Click AP Calc AB Quizzes
Practice Under Real Exam Conditions
Study with Exam-Aligned Questions
Achieve Higher AP Calc AB Exam Scores with Smart Study Tools
Exceptional Explanations
Understand the “why” with our simplified breakdowns of how to approach each question and topic. Our clear question explanations and vivid visuals help you spot and avoid trick answers so you’ll ace the AP Calculus AB exam. Our exclusive technique, backed by cognitive learning principles, maximizes learning and retention.
Flashcards & Notes That Help You Actually Remember
Create digital flashcards to practice the concepts you struggle with most, like how to apply the chain rule or the difference between the product rule and the quotient rule, helping you remember information months later, not just for the next unit quiz. Use My Notebook to organize key concepts from AP Calc practice questions in the format that works best for you, whether that’s bullet points for related rates problems, diagrams showing the relationship between a function and its derivative, or detailed notes on how to find the volume of revolution using different methods. One-click transfer from explanations to your flashcards or notebook means everything you need stays in one organized place.
Track Your Progress and Target Weak Spots
See exactly where you stand with detailed performance tracking across all your AP Calculus AB practice tests and practice questions. Our analytics dashboard shows which topics you're crushing and which ones need more work. Focus your study time on actual weak areas, stop wasting time on stuff you already know, and watch your scores improve.
Pick Your AP Calc AB Prep Package
Pick Your AP Calc AB Prep Package
AP Calc AB Practice Tests
Starting at $39
1400+ AP Calculus AB Practice Questions (MCQs)
Custom AP Calc AB Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
1400+ AP Calculus AB Practice Questions (MCQs)
Custom AP Calc AB Practice Tests & Quizzes
Progress Tracking Dashboard
Pick Your Study Topics
Smart Study Planner
Realistic FRQ Practice with Scoring Guide*
Score-Predicting Full-Length AP Calculus AB Mock Exam*
Print and Digital Study Guide
150+ Check-for-Understanding Questions
Expert-led Video Lessons
* * Coming Winter 2025/Spring 2026
AP Calculus AB Practice Test Reviews
UWorlds multiple choice questions are similar to the ones on the official AP exam and allowed me to time myself for each question. This was very helpful for me as I was able to answer questions faster and could finish the questions on the actual exam. The explanations for each question went in-depth and gave important details pertaining to events in the timeline. Through this, I was able to gain important skills for the exam and get a 5.
See MoreBefore, I had a hard time studying and staying focused because it was just boring, but now with UWorld, not only can I focus, but I actually feel motivated to learn!
The explanations were clear and I could practice the question based on units. I got a 5 in the end!! So, I think it’s very helpful and I’ll be using it to study for my future exams 🙂 You guys provide so many different functions to help students like me, and I really appreciate it, it’s really worth the money.
See MoreAP Calc AB Practice Tests: Frequently Asked Questions (FAQs)
How closely do UWorld's AP Calculus AB practice tests mirror the actual exam?
Our AP Calculus AB practice tests are meticulously designed to replicate the format, difficulty, and content of the real exam. Written by in-house experts, our multiple-choice and free-response questions align with what you’ll encounter on test day including the specific problem types, multi-step reasoning, and justification skills you’ll need to master. Every AP Calculus AB practice problem features a detailed, step-by-step solution so you understand the logic, methodology and mathematics behind every answer, not just the final number.
Why should I use UWorld’s AP Calculus AB practice tests instead of free online materials?
There are free AP Calc AB practice test resources available to help you study but they tend to focus on teaching the general concepts with limited solution and explanation sets. Our AP Calculus AB practice questions are authored by experienced educators and closely reflect the current exam.
With UWorld you get a comprehensive AP Calculus AB practice exam system that includes:
- Exam-level AP Calc AB questions with detailed, step-by-step solutions.
- Customizable quizzes to target specific units, like derivatives or integration.
- Performance tracking to pinpoint your conceptual weak spots.
- Timed modes to simulate the pressure of the AP Calculus AB practice exam.
You’re not just practicing; you’re getting a complete platform designed to help you master the material and improve your score.
Do your AP Calculus AB practice questions cover all the required units and topics?
Yes. Our AP Calculus AB question bank provides comprehensive coverage of all 8 units outlined in the official College Board course and exam description:
- Unit 1: Limits and Continuity
- Unit 2: Differentiation: Definition and Fundamental Properties
- Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
- Unit 4: Contextual Applications of Differentiation
- Unit 5: Analytical Applications of Differentiation
- Unit 6: Integration and Accumulation of Change
- Unit 7: Differential Equations
- Unit 8: Applications of Integration
You can create AP Calc AB practice tests from all topics or build focused quizzes on specific units where you need the most review.
What's the best way to use AP Calculus AB practice tests to aim for a 5?
Start by using topic-specific quizzes to solidify your understanding as you learn new units in class. Before the next unit, create and take at least one AP Calculus AB practice test to then review the step-by-step solutions for every single problem, even the ones you got right. This helps you master the underlying concepts, learn efficient problem-solving methods, and recognize common pitfalls. Use your performance dashboard to identify your weakest units, then create additional AP Calc AB practice tests and quizzes to drill those specific areas.
When is the right time to start using AP Calculus practice questions?
Ideally, you should start using AP Calculus AB practice questions as soon as you begin learning the material in class. Practicing topics and solution techniques like the chain rule or the fundamental theorem of calculus while they are fresh helps reinforce your learning and identifies misunderstandings early. If you’re starting later in the year, don’t worry. Focus on high-yield topics and use our customizable AP Calc AB practice exam generator to target your weakest areas. Consistent, focused practice even 4–6 weeks before the exam can still lead to significant score improvements.
Can I build custom AP Calc AB practice tests focused on specific topics?
Absolutely. Our platform allows you to create customizable AP Calc AB practice tests tailored to your exact study needs. You can focus on broad units, like “Applications of Integration,” or drill down into specific sub-topics. You can set the number of questions to fit your study schedule, allowing you to efficiently target the areas where you need the most practice. After every AP Calc AB practice exam or quiz you can review the integrated performance tracker to track your progress on specific concepts over time.
What score on an AP Calculus AB practice test indicates I’m ready for the real exam?
While there’s no single magic number, a good benchmark is consistently scoring 70% or higher on UWorld’s full-length AP Calculus AB practice tests (across both MCQ and FRQ sections). This is a strong indicator that you are on track for a 4 or 5. If you’re not at 70% yet, don’t panic. Use the performance dashboard data to see exactly which units (e.g., “Differential Equations”) are holding you back, then create targeted quizzes to improve in those areas.
Do these AP Calculus AB practice tests include both Multiple-Choice and Free-Response Questions?
Yes. UWorld’s AP Calculus AB preparation includes hundreds of multiple-choice questions and a robust set of free-response questions (FRQs). You can practice realistic AP Calculus AB exam questions that model the format and style of the real FRQs and our detailed solutions and scoring guidelines teach you how to structure your answers and show your work to earn maximum points, just as an AP grader would expect.
How many full-length AP Calculus AB mock exams should I take before test day?
We recommend that every student take at least one full-length AP Calculus AB mock exam before test day. Practicing under realistic timed conditions is the best way to build stamina, manage your pacing across the different sections and reduce test-day anxiety. UWorld’s AP Calculus AB mock exams are built directly from our deep AB calculus question bank and will give you the realistic interface and style of questions you’ll see on exam day. Furthermore, coming in Spring 2026, we will also offer a pre-built, full-length AP Calculus AB mock exam as part of our AP Calculus AB Online Review Course.
Where can I find free AP Calculus AB practice questions?
You can try free AP Calculus AB practice questions by signing up for UWorld’s free 7-day trial. This will give you access to a sample of our high-quality MCQs and FRQs, complete with the detailed, step-by-step solutions that set our product apart. The free trial also provides a preview of our complete AP Calc AB Course, which includes video lessons and digital study guides to help you master the content.