About SAT® Math Section
The SAT® Math section only tests your proficiency in some aspects of mathematics. It focuses on topics that prove math readiness for future college math courses. In this section, you will find multi-step problems with math scenarios in science, social science, work environments, and other real-life situations. To solve these questions, you need math problem-solving skills, conceptual understanding, and general fluency in math. This comprehensive guide will provide everything about the SAT Math syllabus, format, scoring, and question types. We will also discuss the level of math that you may see on the test and share some review tips to help you prepare better.
SAT Math Format and Syllabus
The paper and pencil SAT Math test is divided into two parts, lasting 80 minutes. However, with the SAT going digital, several changes regarding format, question types, and test duration will be seen. Click on the tabs below to understand the structure of the Math section on both paper and pencil as well as the digital SAT.
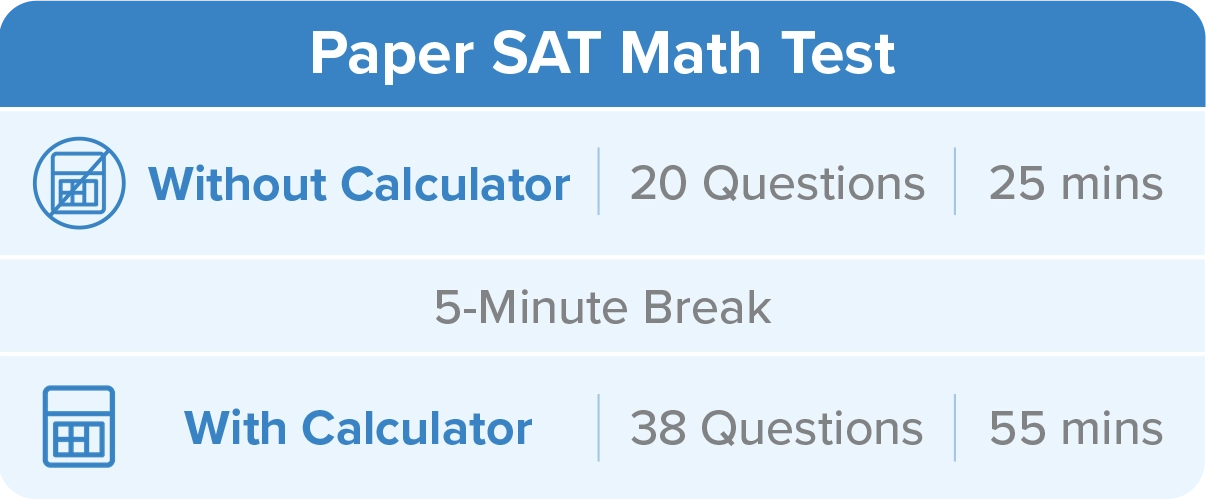
On the paper and pencil format, the SAT Math Test is divided into two parts – a “calculator” portion and a “no calculator” portion, with a total of 58 questions to be completed in 80 minutes. A 5-minute break is provided between the calculator and no-calculator portions of the math test. Here is a breakdown of the number of questions in each portion and the time allotted to answer them.
What type of math questions are on the SAT?
You will find two types of questions in the SAT Math section – Multiple-Choice Questions (MCQs) and Grid-in Questions for which students have to produce their own responses. Out of 58 questions, 45 are MCQs with four answer choices and 13 are grid-ins that require students to produce their own responses.
What topics are on the SAT Math?
The math section on the paper and pencil test will focus on four key areas highlighted in the table below:
| Key Areas | No. of Questions | Percentage of Test |
|---|---|---|
| Heart of Algebra | 19 | 33% |
| Problem Solving and Data Analysis | 17 | 29% |
| Passport to Advanced Math | 16 | 28% |
| Additional Topics in Math | 6 | 10% |
Let’s learn about each of these key areas in detail.
Heart of Algebra
These questions focus on systems of linear equations and functions asking you to solve equations which represent a situation plus establish connections between different representations of linear equations.
Problem Solving and Data Analysis
These questions focus on ratios, percentages, and proportional reasoning asking you to analyze graphical and statistical data, evaluate reports, make inferences, and draw conclusions.
Passport to Advanced Math
These questions focus on the level of math that you will study in higher education courses such as science, economics, math, technology, and engineering.
Additional Topics in Math
These questions focus on geometry, trigonometry, radian measure, complex numbers, and applications of surface area and volume.
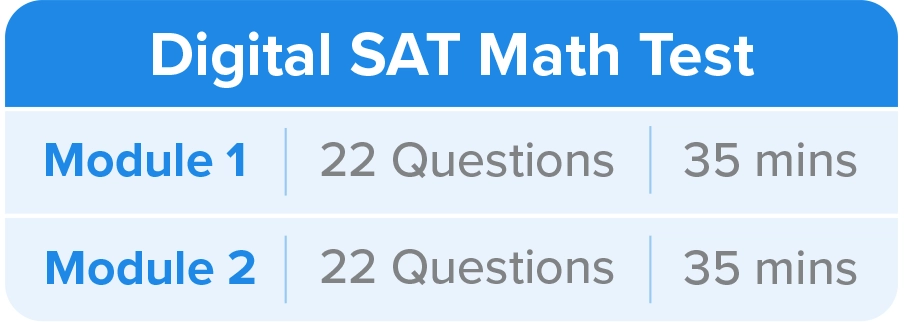
In the digital format, the SAT Math section is composed of two equal-length modules, with 44 questions to be completed in 70 minutes. You must note that, unlike the paper and pencil SAT, you are allowed to use a calculator throughout the Math test for both the modules on the digital SAT. The following table displays a breakdown of the number of questions on each module and the time allotted to answer them.
What type of math questions are on the digital SAT?
Just like the paper and pencil test, you will find both MCQs and student-produced response questions (SPR) on the math section of the digital SAT. According to the College Board®, 75% of the questions on the test will be MCQs, and 25% will be SPRs.
What topics are on the digital SAT Math section?
The math section on the digital test will focus on four key domains highlighted in the table below:
| Key Elements | No. of Questions | Percentage of Test |
|---|---|---|
| Algebra | 13-15 | ≈35% |
| Advanced Math | 13-15 | ≈35% |
| Problem Solving and Data Analysis | 5-7 | ≈15% |
| Geometry and Trigonometry | 5-7 | ≈15% |
Let’s learn about each of these key domains in detail.
Algebra
These questions will require you to analyze and solve linear equations, systems of equations, and inequalities using multiple techniques.
Advanced Math
These questions evaluate your understanding of quadratic, polynomial, exponential radical, rational, absolute value, and other nonlinear equations.
Problem Solving and Data Analysis
These questions check your quantitative reasoning skills about topics like rates, ratios, proportions, and interpretation of one- and two-variable data.
Geometry and Trigonometry
These questions focus on trigonometry, the area and volume of geometric figures like circles, triangles, and more.
To learn more about the important topics and concepts tested on the math section in detail, read our guide to the SAT syllabus.
What Level of Math is on the SAT?
The Math section is based on high school curricula, so, likely, the SAT math topics you encounter will be familiar to you. This test displays what you have learned in high school and your readiness for the basics of postsecondary courses. This section focuses on your problem-solving skills and evaluates your ability to make real-world connections through multi-step problem questions.
Do SAT Math questions get progressively harder?
No, the SAT Math questions do not get progressively harder. The paper and pencil test is a mix of easy, medium, and hard questions.
However, on the digital version, where the first module is a mix of easy, medium, and hard questions, the difficulty level of the second module depends on how you performed on the first module.
Is SAT Math harder than ACT Math?
The SAT and ACT Math tests are different in various ways. The SAT Math test gives you 80 minutes for 58 questions on the paper and pencil version of the test and 70 minutes for 44 questions on the digital version, whereas the ACT Math test requires 60 questions to be completed in 60 minutes. This means that on the SAT Math test you get more time per question than you would on the ACT Math section. In addition, the SAT Math test focuses heavily on algebra and data analysis, while the ACT Math test covers a range of topics including trigonometry, advanced algebraic concepts, and modeling. Ultimately, the difficulty of the test depends on your familiarity with the test format, your overall math skills, and your ability to manage time effectively during the test.
Is SAT Math harder than PSAT?
The math section on the PSAT covers fewer advanced topics and is designed to be a slightly easier version of the SAT. It is generally taken by students during the sophomore or junior year of high school and is often considered a “practice” test for the SAT. However, the PSAT is still challenging. You need to have strong math skills and test taking strategies to score well on it.
Can you skip the Math section of the SAT?
No, you cannot skip the Math section of the SAT, as it makes up 50% of your total SAT score.
How to Calculate Your SAT Math Score?
The SAT math score ranges from 200-800 and is calculated by converting your raw scores to scaled scores. On the paper and pencil test, once your raw score is calculated, it is converted to the test score of 10-40 and then multiplied by 20 to get the scaled score between 200-800.
On the digital test, the raw scores from both modules are added together, and then the total raw score is converted to the scaled score of 200-800. Note that this score conversion is based on the SAT math score chart released by the College Board every year.
Based on your section score, you will also get SAT Math percentiles ranging from 1 to 99 for the paper and pencil version of the test. No percentiles will be reported for the digital test. To understand how scores are calculated and how section scores contribute to your final score, read our SAT scoring guide.
What is the passing score for SAT Math?
The College Board does not mention any passing scores for students. However, for successful college admission, it is good to get more than the average score for a particular year.
What is a good SAT score in math?
A good SAT score in math can be determined by the average SAT math score of a particular year. If you score above the average, it may be considered a relatively good score.
What is the highest math SAT score and how many people get a perfect SAT math score?
The highest SAT Math score is 800. Getting a perfect score is quite rare. Only about 1% of students who take the SAT are able to score 800.
What is the average Math SAT score?
The average SAT math score changes from year to year depending on the total score of all the test takers for a particular year. The average score for the SAT Math section in 2022 was 521.
SAT Math Review Tips
We know that preparing for the SAT Math test can seem overwhelming, but with the right guidance, you will be ready to take the test with confidence. Here are a few things to keep in mind:
- Learn what is on the Math test. It is important to know the format, question types, and duration of the test. Knowing all the basics is a good way to kickstart your test prep.
- Practice as much as you can. There is no better way of improving your math skills than practicing. Learning how to apply all the formulas and developing a thorough understanding of the topics on the test are essential for a strong performance. You can find a compiled list of all the formulas useful for solving the math questions on our SAT Math formula sheet.
- Time yourself. You must practice time management. When you time yourself, it will also help you determine your concentration and testing endurance level while under pressure. This may help decrease test day anxiety as well as boost your performance.
- Focus on your weak points. By analyzing which areas you are struggling with, you can study efficiently. Improving your weaknesses and locking down your strengths will increase your success on the math SAT section.
Lastly, it is crucial to make an effective study plan to complete your preparation on time. Our SAT Math study guide can help you with this and also give you tips on approaching different questions on the test. You can perfect your math skills by using UWorld’s SAT Math practice test. Our in-depth answer explanations and performance-tracking tools will help you get closer to your targeted score.